考虑横向接地应力的沥青路面剪应力分析

张兰峰, 汪海年

(长安大学 特殊地区公路工程教育部重点实验室, 陕西 西安 710064)

在车辆与路面的交互作用中,车辆通过轮胎将荷载传递给路面.在传统路面力学计算中,轮胎-路面接触压力的分布形式被简化为圆形或者矩形均布荷载.但实际上由于轮胎表面花纹的存在,导致轮胎-路面交互作用的复杂性和非均布性,影响到路表面的力学响应与圆形或者矩形均布荷载作用结果存在很大差别[1].根据文献[2-3]研究表明:轮胎路面接触应力的分布情况显著影响路面的力学响应;通过实测与数值模拟静力分析,证明荷载非均匀分布对路面结构的应力作用大于荷载均匀分布.文献[4]研究得出,不同轮压分布形式对路面指标中影响最大的是剪切指标,超载时,轮压非均布下的最大剪应力超过轮压均布下的3倍多.当轮胎荷载作用于路面时,胎肋部位将产生三向应力(竖直应力,横向应力和纵向应力),这些应力不是均匀分布的.车辆的加速、减速、制动和转弯等机械操作也会改变接地应力,尤其是城市道路受到红绿灯和人流的影响,无法高速行驶,操作会在刹车制动、停车静止、启动、行驶(直线、弯道)的状态间转换[5].车辆对路面的作用与其运动状态有关,对于路表面的力学响应影响很大.车辆静止在路面上时,一般只考虑轮胎对路面的垂直力作用;当车辆处于行使状态时,轮胎除了对路面的垂直作用之外,还存在由于轮胎与路面摩擦作用引起的水平切向力(纵向应力);在道路上转弯时,路面还受到向心力的反作用力(横向接地应力),这不仅对路面结构产生不利影响,对车辆的行驶安全也不利.工程实践发现:在沥青路面弯道内侧病害较多,特别是车辙、沿轮迹带的纵向裂缝、推移等,在高温地区这种病害更加明显[6],这些破坏都与剪应力有极大关系.横向接地应力会显著影响近路表的路面应力情况,因而不能被忽视.

为了更好地研究横向接地应力变化对路面剪应力的影响,利用ABAQUS有限元建立三维道路结构模型,在路表施加非均布荷载.鉴于目前中外大部分载重汽车和小汽车都已采用子午线轮胎[7],为此,本研究主要针对沥青路面在子午线轮胎作用下的力学响应,将子午线轮胎(纵向花纹轮胎)荷载简化成作用于路面结构5条可移动的应力、长度及宽度不同的条带荷载,模拟分析在考虑车辆横向力作用下路面剪应力的影响.

1 路面结构三维模型建立

1.1 模型建立假设

① 路面各层间是完全连续的,应力和位移的传导是连续的; ② 路表面作用的荷载与路表面接触面形状一定,接触面上的压力呈均匀分布; ③ 基层、土基材料为线弹性材料,面层材料为黏弹性体.

模型采用典型半刚性基层路面结构,基于沥青路面黏弹性层状结构体系的基本假设,建立ABAQUS三维半刚性基层沥青路面有限元模型.其中x轴为道路宽度方向(横向),y轴为道路深度方向(竖向),z轴为行车方向(纵向).路面结构模型为长×宽×高=6 m×6 m×3 m.

图1为沥青混合料路面结构三维模型.对图1道路模型施加对称的边界条件:横向两侧面设置为XSYMM(UX=URY=URZ=0),纵向两侧面设置ZSYMM(UZ=URX=URY=0),模型底部设置ENCASTRE(U1=U2=U3=UR1=UR2=UR3=0).采用三维六面体八结点线性减缩积分等参单元(C3D8R).模型长度为6 m,只是圆曲线与缓和曲线中的一个微段,为方便建模和计算,模型将6 m的曲线段近似为直线段.

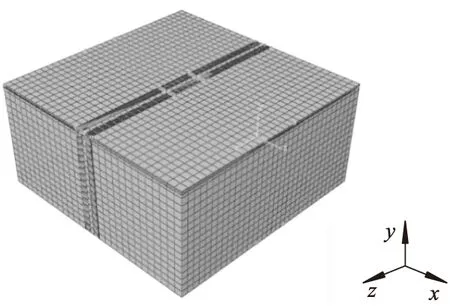
图1 沥青混合料路面结构三维模型

1.2 路面结构参数

为研究动态荷载作用下的路表剪应力响应,故采用回弹模量动态模量.表1为路面材料力学参数[8].

表1 路面材料力学参数

2 荷载作用形式

为了保证行车安全,轮胎胎面刻有花纹以满足轮胎和路面间足够的附着力.花纹的存在,导致轮胎和路面间的接地压力具有非均布性和复杂性.轮胎-路面接触压力的大小和分布形式不同,在路面结构内产生的力学响应,尤其是对轮胎-路面接触区域附近的力学响应差别很大.为了研究分析非均布轮载作用下沥青路面结构的力学行为,参考国内外文献资料,结合我国车辆轮胎的实际使用情况,将子午线轮胎与路面接触区域简化为长度和宽度不同的矩形荷载条组合[9],如图2所示.

图2 轮胎简化模式

2.1 滚动阻力

在实际车辆运行中,车辆对路面的作用不仅有垂直荷载,还有与行车方向相切的水平荷载.车辆对路面的水平作用力受路面线型状况(平面、坡道路面、转弯等)、车辆运行状况(匀速行驶、正常加速、一般制动、紧急制动)等的影响[10].一般情况认为水平载荷跟垂直荷载有一定的线性关系,可用一个水平力系数来描述,即

F=fP,

(1)

式中:F为车辆滚动情况下路面所受水平荷载;P为垂直接地应力;f为滚动摩阻系数.

结合国内外已有轮胎与路面接触效应研究成果,并参考相关的轮胎与路面间接触压力的实测资料,在车辆匀速行驶时,垂直荷载采用标准轴载0.7 MPa,水平荷载在匀速行驶时采用0.010 5 MPa,即滚动摩擦系数f取 0.015[11].模拟中,假设滚动摩擦阻力不变.

2.2 横向接地应力

汽车在曲线上行驶,由于离心力的作用,在轮胎与地面接触处产生与竖直应力垂直的横向分力,该横向分力与车辆垂直力的比值称为横向力系数.横向力系数在车辆运行过程中是个随机变量,受车型、车速、路面状况、行驶轨迹等多种因素影响[12].当轮胎处于直线路段滚动状态时,路面除承受非均匀分布竖向荷载、纵向荷载以外,垂直于行车方向路面还承受非均匀分布的横向荷载,其特点为每一个加载条左右两侧横向应力作用方向相反,幅值不同,但总横向应力合力接近于0[13].但当车辆行驶在曲线段时,轮胎与地面接触产生的总横向接地应力合力不为0,在不设超高地段的曲线段,这个合力不为0的横向接地应力的反作用力就是用于提供车辆转弯的向心力.由于超高设置会部分抵消横向接地应力,因此建立的模型并未设置超高.横向力系数为转弯时的横向力与垂直力的比值,所以横向接地应力T可计算如下:

T=μP,

(2)

式中:T为横向接地应力;μ为横向力系数.

研究[14]表明,横向轮胎接地压力一般为最大垂直轮胎接地压力的15%～50%.据此,本研究中采用的横向力系数为μ=0,0.21,0.35,0.49,以对比不同横向力系数工况下的路面剪应力变化.

2.3 移动荷载的施加

使用有限元软件ABAQUS 建模时,在车辆荷载移动方向上设置两条荷载移动带,每条移动带沿路面结构纵向长度为车辆行驶的距离,荷载带横向宽度为轮胎荷载两个外边缘之间的距离.移动荷载的施加通过在路表面划分荷载移动带来实现.荷载带移动实现是借助用户子程序(user subroutine)平台,使用Fortran语言编写程序 Dload和Utracload以施加垂直荷载和水平、横向荷载.其中Dload用来施加垂直均布荷载，Utracload用来施加水平均布荷载和横向均布荷载，实现车辆荷载沿移动带向前移动.根据荷载带尺寸划分网格,再在划分的单元上施加荷载,将各荷载条根据网格划分为许多小矩形,如图2c所示.轮间距为13.2 cm,设荷载行驶速度v=36 km·h-1.

3 路面受力分析

3.1 路表剪应力分布

图3为不同横向力系数下路表剪应力S12分布.

图3 不同横向力系数下路表剪应力分布

当轮胎处于滚动状态,且不计横向力作用时,路表剪应力分布如图3a所示,正、负剪应力最大值均位于轮胎两侧边缘,中间条带的剪应力略低于边缘条带,且两个轮胎荷载接地范围内(x坐标范围为-0.266 25～0.266 25 m)的剪应力分布近乎关于(0,0)点成反对称分布,最大正剪应力为0.186 MPa,最大负剪应力为-0.177 MPa,轮隙中心的剪应力近似为0.当考虑轮胎与路面的横向力作用时,首先取横向摩擦系数μ=0.21,路表剪应力分布如图3b所示,相对于图3a,剪应力分布数值整体下移;正剪应力减小,负剪应力增大,正、负剪应力最大值仍然位于轮胎两侧边缘;最大正剪应力为0.101 18 MPa,最大负剪应力为-0.281 69 MPa,轮隙中心的剪应力为-0.012 53 MPa.当横向摩擦系数为μ=0.35时,剪应力分布数值继续整体下移,正剪应力继续减小,负剪应力继续增大;最大正剪应力位于轮胎两侧边缘,为0.019 32 MPa,而最大负剪应力位于轮胎中间荷载带,为-0.326 81 MPa,轮隙中心的剪应力为-0.020 72 MPa.当横向摩擦系数为μ=0.49,剪应力分布变化趋势和规律与μ=0.35相同,最大正剪应力位于轮胎两侧边缘,为0.002 79 MPa,而最大负剪应力位于轮胎中间荷载带,为-0.406 09 MPa,轮隙中心的剪应力近似为-0.029 00 MPa.

3.2 轮胎荷载带沿道路深度方向剪应力分布

分别取轮胎5个荷载带的中点和轮隙中心为剪应力计算点.图4分别为横向力系数μ=0,0.21,0.35,0.49时,各点在沿道路0～78 cm深度方向时的剪应力S12分布.取左侧荷载带的5个荷载条中点,A为第1条荷载条中点;B为第2条荷载条中点;C为中间荷载条中点;D为左侧第4条荷载条中点;E为左侧第5条荷载条中点;F为轮隙中心.

由于道路结构层间的力学参数(动态模量、泊松比、密度)不同,剪应力S12在不同层间发生不同程度的突变,以A,B和C点较为突出.不同点位剪应力沿道路深度变化规律不尽相同.A,B和F的剪应力变化规律完全相同,在深度范围为0～4 cm时剪应力按负方向逐渐增加,而4～18 cm剪应力减小.C点除了剪应力在4 cm处出现明显突变,当μ=0,0.21时,剪应力在0～18 cm内变化趋势是逐渐增加;μ=0.35,0.49时,剪应力在0～18 cm内变化趋势是逐渐减小.D,E点变化规律相似,μ=0时,路表剪应力为正值,在0～4 cm内剪应力按正方向增加,4 cm处达到剪应力的最大值,而4～18 cm时剪应力减小.μ=0.21,0.35,在0～4 cm内,剪应力有负变正转换,但数值减小;4～18 cm时剪应力出现由正向负的转变.μ=0.49,在0～4 cm内,剪应力减小;4～18 cm时剪应力增加.表面层底4 cm处是剪应力增减变化的转折点.横向力不同引起的道路结构各层剪应力不同的影响范围主要在沥青面层(0～18 cm)范围内.而在18 cm以下深度,剪应力衰减较快,土基顶面的剪应力几乎为0.

研究表明:横向力不仅影响路表剪应力分布和数值,同样影响沿道路深度方向剪应力的变化规律.横向力系数对道路结构不同深度剪应力的影响显著范围为0～18 cm.根据图4数据分析,不同层间的剪应力存在突变.图5为按照0～18 cm路面层3个不同层位(除路面层外)的层间剪应力突变值中的最大值绘制.

图4 不同横向力系数下沿道路深度方向剪应力分布

图5 不同层位不同点位剪应力与横向力系数关系

图5a表明:各点路表剪应力都随着横向力系数的增加而线性增加,线段斜率范围为-0.360～-0.540,其中对轮隙中心路表的剪应力影响最小,线段斜率为-0.060.横向力系数与其他层位不同点的剪应力也呈线性增加关系,而且图5b-d中的线段斜率几乎相同.图5b线段斜率几乎都为-0.200,图5c几乎都为-0.140,图5d都为-0.078.根据图5中线段的斜率大小比较可得:横向力系数不同,对路表面的剪应力影响最大,对路面层内其他层位剪应力的影响依次减小.

4 结 论

1) 路表剪应力分布与横向力系数有显著关系.中间荷载带的负剪应力逐渐增加并超过边缘剪应力,最大负剪应力出现的位置发生变化,由轮胎边缘向中间荷载带移动;最大正剪应力出现的位置一直位于轮胎两侧边缘,但是数值在减小.当横向力系数增大时,各荷载带作用下的正剪应力减小,负剪应力增加.这也解释了路面弯道内侧,在夏季高温、重载交通情况下,容易出现车辙、推移、裂缝的原因.

2) 由于道路结构层的力学参数(动态模量、泊松比、密度)不同,导致剪应力在不同层间发生不同程度的突变.不同点位剪应力沿道路深度变化规律不尽相同.在沥青面层深度0～18 cm范围内,横向力系数对剪应力变化影响显著;在18 cm以下深度,剪应力衰减较快,土基顶面的剪应力几乎为0.横向力不仅影响路表剪应力分布和数值大小,同样影响沿道路深度方向剪应力的变化规律.

3) 横向力系数与不同点位剪应力呈线性增加关系,其中横向力系数对路面剪应力影响最大,对沥青路面内其他层位剪应力的影响依道路结构深度增加而减小.

)

[1] 刘美丽.轮胎路面交互作用数值模拟分析[D].哈尔滨:哈尔滨工业大学,2013:2-4.

[2] SIDDHARTHAN R V,KRISHNAMENON N, EL-MOUSLY M. Investigation of tire contact stress distributions on pavement response[J]. Journal of Transportation Engineering, 2002,128(2):136-144.

[3] ELSEIFI M A. Viscoelastic modeling and field validation of flexible pavements[J]. Journal of Engineering Mechanics, 2006,132(2):172-178.

[4] 胡小弟,孙立军.沥青路面车辆超载定义分析[J].同济大学学报(自然科学版),2007,35(12):1612-1616.

HU X D,SUN L J.Definition analysis of vehicle overload acting on asphalt pavement[J].Journal of Tongji University(Nature Science),2007,35 (12): 1612-1616.(in Chinese)

[5] 姚占勇,田腾辉.不同轮压分布形式对半刚性路面结构力学响应的有限元分析[J].山东大学学报:工学版, 2009,39(6):105-110.

YAO Z Y, TIAN T H. Study of the mechanics response of semi-rigid pavement structure under different tire pressure distributions[J]. Journal of Shandong University(Engineering Science),2009,39(6):105-110.(in Chinese)

[6] WANG H. Analysis of near-surface cracking under critical loading conditions using uncracked and cracked pavement models[J]. Journal of Transportation Engineering, 2013, 139(10): 992-1000.

[7] 肖兴强,张立宏,艾长发,等.弯道超高路段沥青路面的力学响应分析[J].重庆交通大学学报(自然科学版),2008,27 (1):53-56.

XIAO X Q,ZHANG L H,AI C F,et al. Structural response on superelevation sections of asphalt pavement[J]. Journal of Chongqing Jiaotong University(Natural Science),2008,27 (1): 53-56.(in Chinese)

[8] 廖公云,黄晓明.ABAQUS有限元软件在道路工程中的应用[M].南京:东南大学出版社,2008:184-185.

[9] 吕光印.柔性基层沥青路面 Top-Down 开裂机理研究[D].西安:长安大学,2008:35-38.

[10] 谢水友,郑传超. 水平荷载对沥青路面结构的影响[J]. 长安大学学报(自然科学版), 2004,24 (2):14-17.

XIE S Y, ZHENG C C. Influence of horizontal loads on asphalt pavement structure[J]. Journal of Chang′an University(Natural Science Edition), 2004,24 (2):14-17.(in Chinese)

[11] 郑仲浪.重载车辆作用下沥青路面层间力学行为研究[D].西安:长安大学,2010:45-48.

[12] 李明松.典型轮胎非均匀接触应力获取及其作用下的路面TDC开裂分析[D]. 哈尔滨:哈尔滨工业大学,2015:45-48.

[13] 蒋隆建,程建川.基于车辆动力学分析的道路平曲线处横向力系数研究[J].交通信息与安全,2004,30(5): 65-68, 80.

JIANG L J,CHENG J C. Lateral friction coefficient of highway horizontal curve based on vehicle dynamic ana-lysis[J]. Journal of Transport Information and Safety,2004,30(5): 65-68, 80.(in Chinese)

[14] 董泽蛟,谭忆秋,欧进萍. 三向非均布移动荷载作用下沥青路面动力响应分析[J]. 土木工程学报, 2013,46(6):122-130.

DONG Z J,TAN Y Q,OU J P. Dynamic response analysis of asphalt pavement under three-directional nonuniform moving load[J]. China Civil Engineering Journal, 2013,46(6):122-130.(in Chinese)