复合材料开孔薄壁加筋板剪切屈曲及后屈曲研究
陈 静,沈安澜
(中国直升机设计研究所,江西 景德镇 333001)
0 引言
新时代直升机结构大量采用复合材料,而复合材料承力结构因为工艺或减重的需要常常采用开孔设计,开孔复合材料在受载时会进入非线性弯曲变形阶段,可能出现极值型屈曲和相继的后屈曲变形,具有可观的后屈曲承载能力[1],即复合材料的最终承载能力取决于后屈曲载荷。因此,准确地分析开孔复合材料的屈曲和后屈曲特性对预测开孔复合材料承载能力的影响规律,对于直升机复合材料结构的应用非常重要。国内外学者针对复合材料开孔各种载荷下的屈曲和后屈曲问题进行了相关研究。F.Pierron[2]进行了开孔复合材料层合板受张拉载荷情况下试验结果的损伤分析。Joung Hwan LeeH[3]通过试验研究了开孔复合材料层合板的受压失效行为。C.SOUTIS[4]分析了开孔复合材料层合板在两轴向载荷下的孔边应力分布。P.BERBINAU C[5]对开孔复合材料层合板在多轴向拉一压载荷下的应力和失效进行了分析。KIm[6]等对中心圆形开孔复合材料层合板受到的压缩、剪切和温度混合载荷等不同参数对结构屈曲和后屈曲响应的影响进行了有限元仿真分析。黎增山[7]进行了开孔复合材料层合板拉伸的损伤分析。李军[8]等对含开孔和补强的蜂窝夹芯层合结构的屈曲进行过分析。
现有文献中多为研究复合材料层合板开孔后的承载能力变化情况,而对复合材料薄壁加筋板开孔研究较少,文献多数对拉伸、压缩载荷下的屈曲和后屈曲特性进行分析,而对剪切载荷下结构的承载能力没有足够重视。特别是国内有关复合材料薄壁加筋板剪切载荷下的屈曲及后屈曲特性文献不足。近年来,随着复合材料薄壁加筋板的在直升机结构件的大量应用,结构件失效主要受剪切载荷影响,所以研究开孔复合材料薄壁加筋板的剪切承载能力有十分重要的意义。本文研究对比复合材料薄壁加筋板开孔剪切试验,采用有限元数值模拟的方法对开孔加筋板进行了屈曲及后屈曲分析,与试验结果进行比较,得到较好的一致性,为复合材料加筋板开孔的屈曲及后屈曲有限元分析提供一定的参考。
1 复合材料开孔加筋板剪切数值分析
本文以某直升机重要部段处开孔复合材料薄壁加筋板结构为对象,分析其承载能力。由于目前暂无理论计算开孔复合材料加筋板屈曲载荷的方法,本文使用有限元ABAQUS软件对该开孔结构进行了数值模拟分析。
1.1 开孔加筋板结构形式
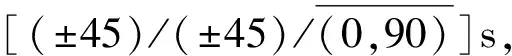
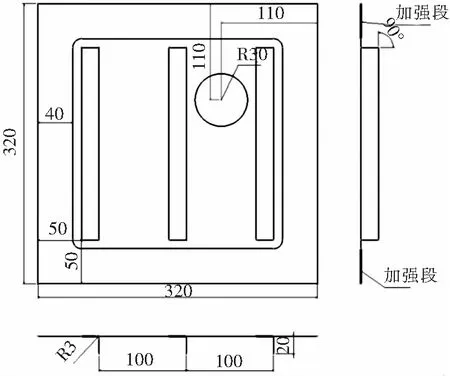
图1 开孔加筋板尺寸示意图
1.2 初始有限元模型
采用四节点减缩积分厚壳单元建立初始有限元模型,筋条与面板成一体建立,共19499个节点、4488个单元,初始有限元模型示意图如图2。
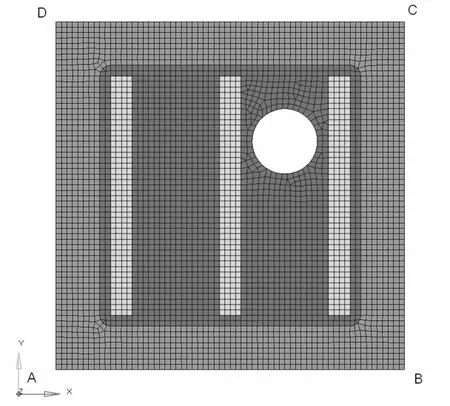
图2 初始有限元模型图
对模型施加实际约束,通过计算得到开孔结构的初始屈曲载荷为12.29kN。
2 复合材料薄壁加筋板开孔剪切试验
2.1 试验件安装及试验设备
为验证有限元模拟计算结果的有效性并确定部分参数,本文对图1的开孔加筋板结构进行了剪切试验。该试验是在大型材料试验机上进行,试验装置如图3所示。试验夹具由高强钢制作,采用四连杆框架试验夹具,由销钉连接的整体双层框架组成,每根连杆上钻有一排螺栓孔。试验夹具连杆应有足够的刚度,防止在加载过程中变形。在复合材料加筋板剪切试验中,数据采集系统可采集到剪切过程中的载荷、应变等参数。如图4所示,试验件正面布置10枚应变片及3枚应变花,反面布置4枚应变片及3枚应变花。

图3 试验件和传感器安装
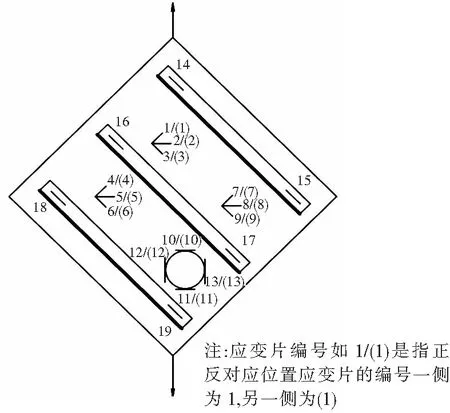
图4 剪切试验应变片布片位置图
2.2 试验分析
对6件开孔剪切试验件的试验结果表明,试验件上下两对角出现裂纹,后沿纵向对角线同时向中间扩展,最终沿孔横向断裂。其中5件试验件的左下侧筋条完全脱掉或被撕断,1件试验件的中间筋条完全脱掉,试验结果见表1。

表1 试验结果
取6号试验件分析,断裂结果如图5。试验件平均破坏载荷为59.38KN,试验加载曲线见图6。

图5 6号试验件断裂图
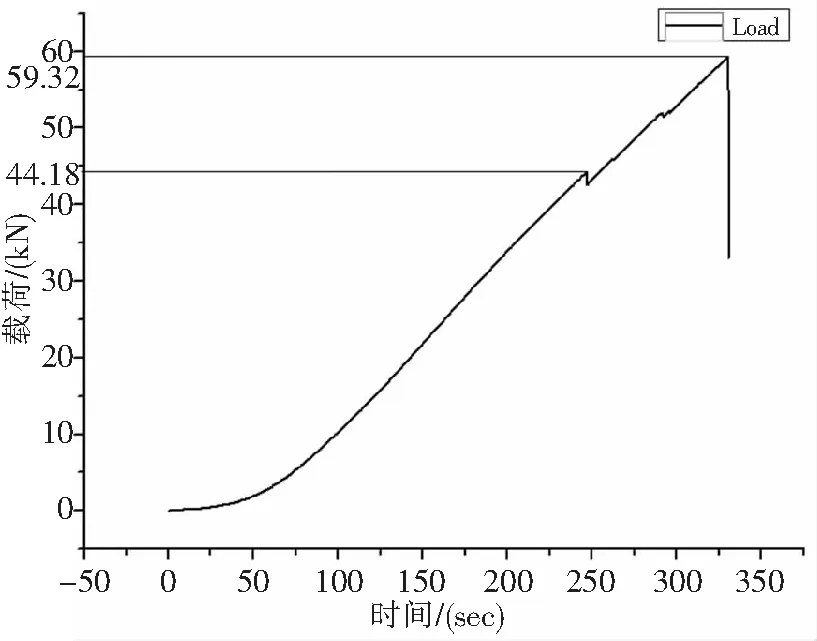
图6 试验加载图
根据图5可知,加筋板在开孔后,在试验件上下两对角及开孔处均出现裂纹,说明开孔是导致复合材料薄壁加筋板破坏的重要原因,因此预测复合材料开孔薄壁加筋板的承载能力非常重要。
3 数值分析与试验对比分析
3.1 初始屈曲分析
为确定影响有限元计算结果与试验结果一致性的因素,本文引入多种参数,将计算后的初始屈曲载荷进行对比计算,从而得到最接近实际结果的有限元模型。
1)网格密度
建立不同网格模型2(网格大小约为面板宽度的1%),采用相同约束进行计算,计算结果与之前网格模型1(网格大小约为面板宽度的2%)计算结果及试验结果对比见表2。

表2 不同网格密度计算结果
通过表2可知,较低密度的网格计算结果更接近实际,且网格划分过细会影响计算速度甚至无法计算。
2)引入胶层
虽然实际结构中面板与筋条通过胶层连接,但由于面板与筋条之间的胶层参数会随试验环境变化而变化,因此在有限元模型中不考虑引入胶层。
根据上述对比分析结果可知,不引入胶层的较低密度的网格模型结果更接近试验值,因此采用该模型模拟复合材料加筋板进行屈曲分析较为合理。
3.2 后屈曲分析
在上述的有限元模型的基础上建立基于Hashin失效准则的渐进损伤仿真模型,采用risk算法实现后屈曲模拟分析计算,取不同的初始几何扰动值进行后屈曲分析,得到的计算结果与试验值对比见表3。
通过表3可知,不同初始缺陷的引入对最大破坏载荷的结果影响较大,且收敛效果不一样,模态阶数越多,因子按比例下降的计算结果越接近实际。
综合上述对比分析结果可知,不引入胶层且引入前五阶模态的初始几何扰动值的低密度网格模型模拟复合材料加筋板进行后屈曲分析较为合理。计算得到的剪切应力图与试验结果对比如图7所示。从图7可知,计算分析模型应力趋势与试验结果一致。

图7 有限元模型应力图及试验结果对比
3.3 模拟与试验的应变对比
为进一步修正和确认屈曲和后屈曲分析方法,对有限元模型施加相应载荷,通过对比分析测点应变值来进一步验证该模型的正确性。
开孔试验中测点2正反两面的应变-载荷曲线如图8所示(试验值为选取一典型试验件的结果,下同)。正反两面的应变曲线有明显的反向分离,说明发生了局部屈曲。
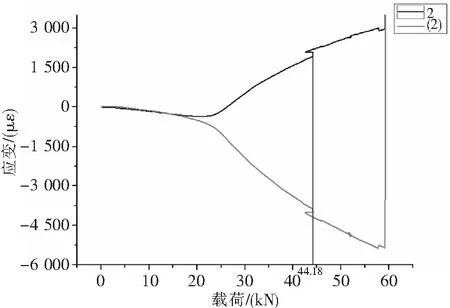
图8 2号测点载荷应变曲线
试验值与有限元应变值对比如图见图9-图11。
通过图9-图11可以看出,在结构失稳之前,应变随载荷的变化近似呈线性关系。失稳后,筋条、开孔部位的应变随载荷的增大而增大,且壁板正反面的应变开始分离,说明壁板的一部分轴向位移向面外位移转化,并且载荷向筋条及开口处转移。在加载过程中,尖端部位的筋条端部和面板的连接胶结界面首先发生破坏导致应变的下降,并使得筋条中部及开口处的承载进一步增加,最终导致结构的破坏。试验值与有限元仿真结果拟合度较高,且应变变化趋势一致,说明仿真结果能较好地反映试验件的破坏规律,验证了仿真计算方法的有效性。
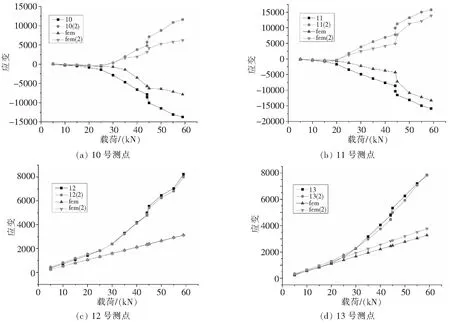
图9 开口处测点的试验和有限元应变值比较
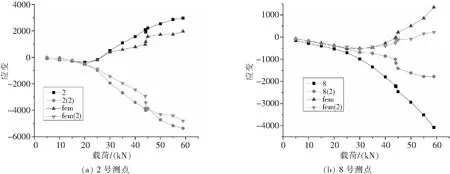
图10 面板处测点的试验和有限元应变值比较
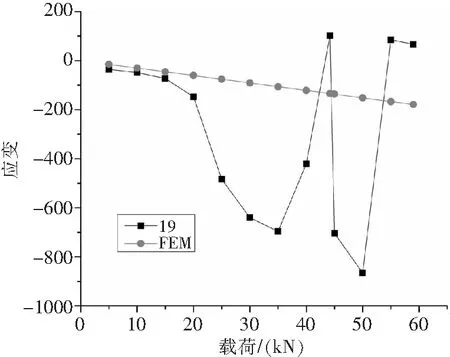
图11 筋条尖端部位处测点的试验和
3.5 其他试验验证
为验证上述有限元数值模拟的通用性,用相同方法建立另一开孔复合材料薄壁层压板结构有限元模型,并对其进行加载试验分析,得到结果:结果趋势图见图12;载荷对比见表4。

图12 试验断裂图与有限元模型分析应力图对比
根据图12及表4可知,采用相同方法计算的有限元结果与试验结果趋势一致,且误差在有效范围内。说明Abaqus软件建立的基于Hashin失效准则的渐进损伤仿真模型,采用risk算法实现后屈曲模拟分析的方法对于分析复合材料开孔薄壁板结构是有效的。

表4 有限元计算结果与试验结果对比
4 不同孔径的薄壁加筋板后屈曲特性有限元分析
根据以上结论可知,可通过该仿真计算方法及模型,分析不同开孔孔径及对薄壁加筋板屈曲及后屈曲的影响规律。
本文在图1中加筋板开孔中心位置开不同孔径的孔,孔直径分别为10mm、20mm、30mm、40mm、50mm,结合之前的60mm计算结果共6种情况进行对比分析,得到的数据见表5。
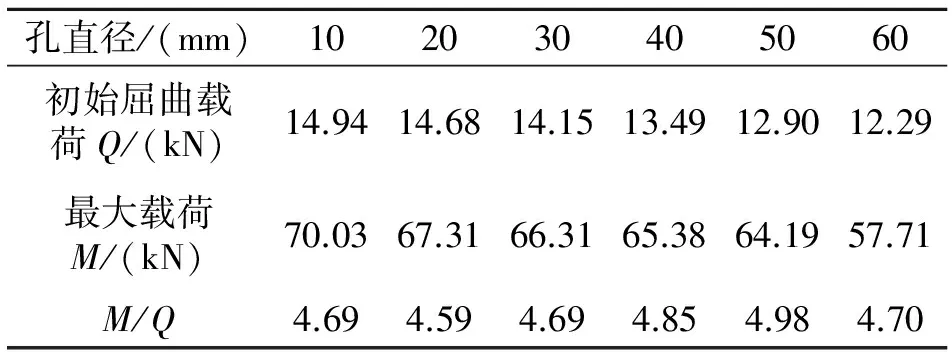
表5 不同孔径下的薄壁加筋板屈曲及后屈曲载荷仿真结果
通过表5可知,开孔薄壁加筋板在局部失稳之后仍有一定的承载能力,开孔孔径越大,初始屈曲载荷及最大破坏载荷越小。对比表1试验结果及表5仿真结果可知,开孔加筋板的最大破坏载荷与初始屈曲载荷呈倍数关系,且大致在3.6~4.9倍之间,因此可以通过初始屈曲载荷来预测复合材料开孔薄壁加筋板的最终承载能力。
5 结论
复合材料开孔薄壁加筋板在局部失稳之后仍具有一定的承载能力。复合材料开孔薄壁加筋板在剪切载荷下,首先面板发生局部失稳,载荷向筋条转移,随后面板和筋条端部的连接胶结界面发生损伤,筋条中部的承载进一步增加,然后载荷沿着开口方向扩展,最终导致结构的破坏。说明在进行复合材料加筋板设计时要加强筋条端部与面板之间的细节设计,防止面板失稳后引起界面的损伤且应避免开孔的尺寸过大。
对于薄壁结构,试件的制造缺陷和边界条件对结构的力学行为具有较大影响,从而导致试验值和模拟值存在一定偏差。同时,当结构发生局部屈曲后,可能随时发生破坏,因此在复合材料开孔薄壁结构的后屈曲分析中引入高阶数缺陷更符合实际情况。在模型中添加胶层单元对结构总体行为有较大影响,需要注意,因此在实际设计过程中可以用不含胶层单元的模型预测结构的屈曲载荷和失效模式。
通过有限元分析与试验结果对比可知,本文采用的有限元数值模拟方法对复合材料开孔薄壁加筋板进行的屈曲及后屈曲分析,与试验结果取得较好的一致性,说明采用risk算法、Hashin失效准则的有限元模型可较准确地预测开孔对复合材料承载能力的影响规律,为复合材料加筋板开孔的屈曲及后屈曲模拟分析提供一定的参考。
[1] 朱菊芬,杨海平,汪 海,等.复合材料加筋板壳结构的后屈曲强度及破坏分析程序系统[J].计算结构力学及其应用,1996,13(4):489-493.
[2] Pierron F,Green B,Wisnom M R,et a1.Full-field assessment of damage process of laminated composite open-hole tensile specimens.Part II:Experimental Results.Composites Part A:Applied Science and Manufacturing,2007,38(11):2321-2332.
[3] LEE J H.Uniaxial Compressive Behaviour of Carbon Fibre-Epoxy Laminates-Part 2:Notched[C].EU-Korea conference on science and Technology,2010,135:175-189.
[4] Soutis C,Filiou C.Stress Distributions around Holes in Composite Laminate Subjected to Biaxiaal Loading[J].Applied Composite Materials,1998(5):365-378.
[5] Berbinau P,Filiou C,Soutis C.Stress and failure analysis of composite laminates with an inclusion under multiaxial compression-tension loading[J].Applied Composite Materials,2001(8):307-326.
[6] Kim Y H,Noor A K.Buckling and Post Buckling of composite Panels with Cutouts Subjected to Combined Loads[J].Finite Elements in Analysis and Design,1996(22):163-185.
[7] 黎增山,关志东,何 为,等.复合材料层板开孔拉伸损伤分析[J].复合材料学报,2012,29(1):169-175.
[8] 李 军,向志海,薛明德,李贵婷.含开孔和补强的蜂窝夹芯层合结构的屈曲分析[J].清华大学学报,2006,46(2):284-288.

