国外旋翼桨叶弹性变形测量方法综述

孟 微，赵国宏

(1.中国直升机设计研究所 直升机旋翼动力学重点实验室，江西 景德镇 333001;2.中国兵器工业试验测试研究院，陕西 华阴 714200)

0 引言

随着复合材料技术的发展，直升机旋翼设计有了很多新的变化。20世纪60年代开始，无铰旋翼和无轴承旋翼的陆续出现提高了旋翼的性能，进而提升了直升机的综合性能。这些新型旋翼的诞生在带来结构简单、重量轻等诸多优点的同时，也带来了复杂的动力学问题。传统的直升机采用铰接式桨毂，桨叶在挥舞、摆振、扭转方向的弹性耦合很小，从动力学角度来看，这种设计的优点就在于用现有理论可以很好地计算出它的动力学性能。新型旋翼无铰、无轴承的特性则会产生复杂的非线性挥舞、摆振、扭转运动之间的耦合问题。旋翼动力学性能对这些耦合运动都极为敏感，因此在计算其动力学性能时，必须重新考虑这些问题。

利用旋转桨叶模型准确地测量数据，验证桨叶模型理论的适用性与可靠性在国外已开展多年并日趋成熟。本文就国外已有的旋翼桨叶弹性变形测量方法作简单的介绍，综合对比分析各方法的优劣。

1 光学测量方法

桨叶弹性变形测量方法大致分为两类，即光学测量方法和传感器测量法。光学测量方法在测试领域是目前较为热门的研究，是随着激光、电子等技术的发展而发展起来的，目前来讲是较为先进的技术。光学测量方法的特点是针对桨叶弹性变形的测量，使用光学仪器，不接触测试件，且测试获得的结果即为位移变化量，无需进行大量复杂的间接转换。光学测量方法主要有：光栅照相法、立体图像识别法和立体图像识别改进法。

1.1 光栅照相法(FCM)

光栅照相法，non-intrusive optical fringe correlation method，简称FCM方法，又称为projected grid method，PGM方法[1]，该方法可以得到桨叶挥舞角和扭转角结果，但无法得到摆振角。首先在旋转中心与桨毂中心(坐标原点)相重合的地面水平转台两端分别安装光栅投影仪和照相机，安装角度要求保证光栅和拍摄范围覆盖全部桨叶，且在整个试验过程中保持不变。试验时用光栅投影仪对整个桨叶表面投射光栅，然后由照相机拍摄下光栅变化。投影仪与Z轴的夹角为β，照相机与Z轴的夹角为α，由此可以得出挥舞方向位移(deflection)与光栅Y方向变形量(image displacement)的几何关系(见公式1)。再根据桨叶不同半径处的位移变化结果可以得出其挥舞角。桨叶扭转角可直接根据其与光栅X方向夹角的几何关系确定。

(1)

1.2 立体图像识别法(SPR)

立体图像识别法(stereo pattern recognition，简称SPR)是通过测量沿桨叶展向分布的各点在挥舞、摆振方向的位移量，从而获得桨叶挥舞角、摆振角及桨叶弹性变形产生的扭转角的方法。具体原理是用照相机分别拍摄装有反光标记的桨叶在静止状态和旋转状态下的照片，将两状态下的照片对比获得每一个固定反光点在旋转坐标系X、Y方向的变化量，再根据X、Y方向变化量与桨叶挥舞、摆振位移的几何关系(公式1)确定沿桨叶展向各点的挥舞、摆振位移，最终获得挥舞角和摆振角。桨叶弹性扭转角则是通过某一展向位置处前后缘两点在Z方向的位移差值求出扭转角，再减去桨叶根部的扭转角和桨叶预扭角即为其弹性扭转角，该方法的最大误差为0.52°。

在文献[2][3]HARTⅡ桨叶运动测量的试验中，试验台下方以旋转坐标原点(桨毂中心)为中心的同一半径下分布四台照相机，一对用于拍摄桨盘前行边，另一对拍摄桨盘后行边。分别在方位角90°和135°位置处安装两台桨尖侦测照相机(BTD)，用来确定桨尖在水平、垂直方向的位移变化。试验前，将桨叶下表面涂黑并安装白色反光标记，反光标记沿展向平均分布在桨叶前缘(0.228弦长)、后缘(0.993弦长)两排，每排18个。试验时每台相机在每个状态拍摄50至100幅照片，最终结果为所得数据的平均值。

1.3 立体图像识别改进法(照相测量法)

照相测量法是为了提高测量精度在原有的SPR的方法上进行了改进，以获得更高精度的桨叶挥舞角、摆振角及弹性扭转角的方法。较原方法不仅增加了桨叶上的反光标记，而且在试验风洞壁上按方阵高密度地安装了大量的反光标记，并增加了照相机的数量(8台)。测量结果不再是以桨毂中心为坐标原点的坐标系中的结果，而是在固定方阵坐标系中的，从而避免了因坐标系原点不稳定带来的误差。试验照片的测量结果与挥舞、摆振位移的转换即为固定方阵坐标系与旋转坐标系的转换。所以需要在旋翼桨毂上做反光标记以确定其在固定方阵中的位置。在UH-60旋翼系统全尺寸桨叶测量试验中，采用的就是该方法[4]。

照相测量法的具体原理是：首先明确旋翼轴在风洞壁上光标方阵中的位置，确定其前倾角；然后将风洞中的光标和桨叶上的光标位置用非线性最小方差拟合的方法估算出在零相位时桨叶在固定方阵坐标系中(XYZ)的位置；桨叶的扭转角将被投影到绕X轴转动，挥舞角被投影到绕Y轴转动，摆振角投影到排除前倾角后的绕Z轴转动。

2 传感器测量方法

传感器测量方法是比较传统的测试方法，它的特点是测试设备简单，成本较低，但测量获得的信号需通过事先建立好的模型关系计算方可得到所需结果。该方法应用较早，于20世纪70年代由RAE(皇家航空中心)在测量旋转桨叶的振动模态时建立并发展起来，在旋翼桨叶变形测量中有着不可替代的作用。在长期的试验应用中，该类方法日趋成熟，已经在许多不同的试验测量中得到成功的运用。该类方法主要有kinematical方法和传统的应变测量方法。

2.1 kinematical方法

kinematical方法[5]是一种理论计算与试验测量相结合的方法，该方法通过将传感器测量的线性位移或角位移信号用kinematical方法处理，即利用铰的几何矩阵与测量系统得到一种变换关系，计算出所需的桨叶挥舞、摆振、扭转角。其中摆振、挥舞、扭转角与传感器线位移与角位移的关系表达式为kinematical方程。该方法比较成熟，已经在许多不同的飞机上得到成功运用。

该方法是把其他位移变化(传感器可以简单测量得到)应用合适的运算法则换算成角位移，从而取代直接测量三个方向的角位移。通过传感器线位移与角位移求出摆振、挥舞、扭转角，并将该矩阵求逆得到用该矩阵表达的关系式，即kinematical方程，其最大优点是大大减少了传感器的安装数量，有些地方甚至可以达到仅安装一个传感器便可完成测试的效果。其关键在于桨毂和桨叶上位移传感器安装位置的合理性。

2.2 应变电测法

应变电测量方法(简称SPA技术)是20世纪70、80年代由RAE[1-3]皇家航空研究中心发展的一套方法，是旋翼桨叶变形测量中最早使用的方法，同时也是目前力学试验中应用最广泛的、最为简单的电阻应变测试法。

(2)

如果第二个要求也成立，那么应变响应也可表示为：

(3)

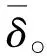
(4)

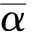
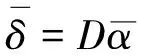
(5)

其中D是δ1，δ2，δ3，……δp的(nxp)矩阵。

总的来说，应变片的数量和分布是由所要测量的位移量的复杂程度决定的，比如测量旋翼桨叶的低阶模态时所需要的应变片数量就比测量高阶时少。考虑到噪声限制，应变响应的数量r和所需测量位移点的数量n要大致相同，应变片的分布也要大致沿着桨叶结构分布。

3 综合比较

通过前面对各种方法的详细介绍，综合分析两大类桨叶弹性变形的测量方法，文中所阐述的光栅照相法、立体图像识别法和立体图像识别改进法等光学方法，如果没有足够复杂的光学设备，往往不能保证测量精度，也不适合于确定相位关系，而且试验成本较高。

虽然SPA技术是早期发展起来的，但相比传感器测量方法里各种不同的位移传感器，应变片更容易安装在桨叶上。其最大优点是质量小，低成本，不需要相位特征；缺点是由于桨叶的挥舞、扭转耦合问题及应变片在桨叶上布置粘贴问题，很难保证复杂外形桨叶的测量精度，例如有后掠尖削的ERATO[1]桨叶。各种方法的优、缺点对比见表1。

表1 各种方法的综合比较

4 结束语

总而言之，目前的旋翼桨叶弹性变形测量方法中，并没有哪一种方法可以取代其他方法，各有优缺点。针对较为频繁和常规的试验来说，考虑到应变片成本和微小加速计及其他方法成本的比较，在直升机旋翼桨叶的悬停及风洞振动模型测量中，SPA技术仍是目前最为经济实用且最常采用的方法。

[1] Muller R H G, Pengel K, Van der Wall B G. Blade Deflection Measurement at the Low Noise ERATO Rotor[C].26th EUROPEAN RORORCRAFT FORUM, The Hafue, Netherlands, September 2000:104.

[2] Schneider O, Van der Wall B G, Pengel K. Final Analysis of HART-II Blade Deflection Measurement[C].29th European Rotorcraft Forum, Friedrichshafen, Gemary, September 2003.

[3] Schneider O, Van der Wall B G, Pengel K. HART-II Blade Motion Measured by Stereo Pattern Recognition (SPR)[C]. 59th Annual Forum of the American Helicopter Society, Phoenix, USA, May 6-8 2003.

[4] Olson L E, Abrego A I, Barrows D A, et al. Blade Deflection Measurements of a Full-Scale UH-60A Rotor System[C]. The Ameri--can Helicopter Society Aeromechanics Specialist’ Conference, January 20-22 2010.

[5] Attilio C, Alessandro L. Measuring Blade Angular Motions: a Kinematical Approach[C].30th European Rotorcraft Forum，Augusta 2004.

[6] Gaukroger D R, Hassal G J W. Measurement of Vibratory Displacement of a Rotating Blade[J].Vertica , 1978(2):111-120.

[7] Walker A R. Further Application and Development of Strain Pattern Analysis[C].8th European Rotorcraft and Powered Lift Forum, 31 August-3 September,1982.

[8] Tourjansky N, Szechenyi E. The Measurement of Blade Deflections A New Implementation of the Strain Pattern Analysis[C].Associantion Aeronautique et Astronautique de France,1992.