对称区域上二重积分的简化计算方法

葛淑梅

（焦作大学基础科学系，河南 焦作 454003）

对于连续的奇偶函数在对称区域上二重积分的简化计算早有讨论，但当函数不具备奇偶性或不考虑函数的奇偶性，遇到对称区域上的二重积分时，有没有较好的计算方法呢？这里我们由一元连续函数在对称区间上定积分的一种计算方法，类推出二元连续函数在对称区域上二重积分计算的一种方法，使用一般方法难于计算（或计算量较大）的二重积分得以简化计算。

对称区间上定积分的计算有下面的命题成立。

若 f(x)是定义在区间[-a，a]上的连续函数，则有下式成立。

此式是高等数学在讨论对称区间上奇偶函数的定积分计算时证明成立的，它的成立表示一元连续函数f(x)在关于y轴对称区间上的定积分等于f(x)+f(-x)在一半区间上的定积分。借助该式可以使一些定积分的计算化难为易，化繁为简。

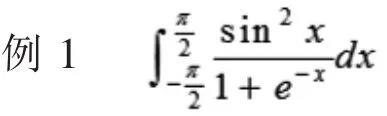
解：注意到积分区间的对称性，由（1）式可得

由此例可见，被积函数不具备奇偶性，直接计算又相当困难，但借助于（1）式转换后被积函数就变得很容易积分了，可见此方法运用得好，能起到简化计算的重要作用。那么，计算二重积分时，若积分区域具有某种对称性，是否也有相应的结论成立呢？请看下面的分析讨论。

(1)设 D 是关于 y 轴的对称区域，f（x，y)为 D上的连续函数，则

其中D1是D被y轴分割所得的一半区域，习惯将D1视为y轴右侧区域，即x≥0部分。

因为此时区域D用不等式组可表示为

显然区域D是关于y轴对称的区域，由（2）式可得

同理，我们可以得出二重积分在对称区域上计算的一系列结论。

（2）设 D 是关于 x 轴的对称区域，f(x，y)为 D上的连续函数，则

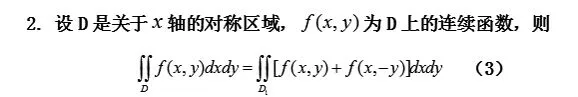
其中D1是D被x轴分割所得的一半区域，习惯将D1视为x轴上侧区域，即y≥0部分。

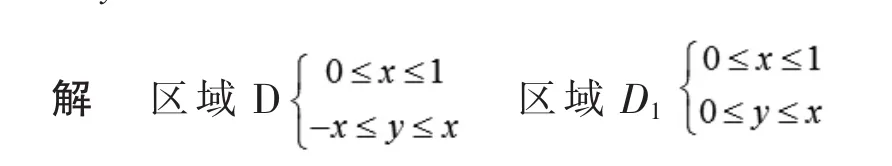
区域D是关于x轴对称的区域，由（3）式可得

（3）设 D 是关于原点 O 的对称区域，f(x，y)为D上的连续函数，则

其中D1是D关于原点O对称的一半区域。

解：区域D1

区域D2

D是D1与D2的和，且D1与D2关于原点O对称，由（4）式可得

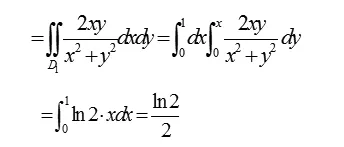
（4）设D是既关于x轴同时又关于y轴对称的区域，f(x，y)为 D 上的连续函数，则

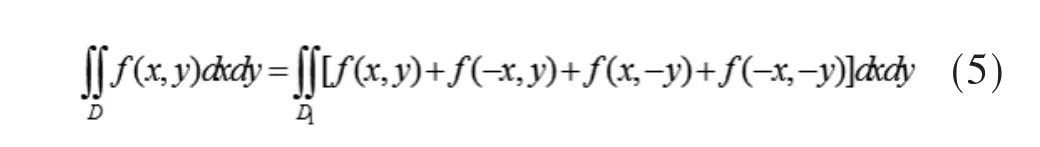
其中 D1是D被x轴、y轴分割所得的四分之一区域，习惯将D1视为第一象限的区域，即x≥0，y≥0部分

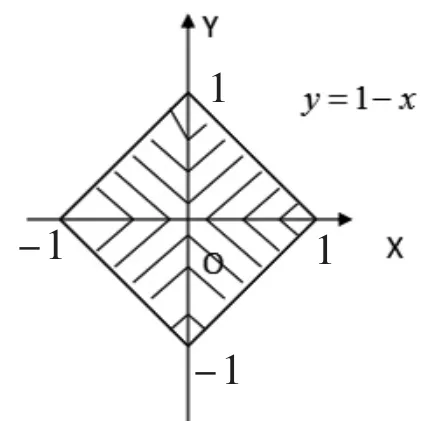
（5）设 D是关于直线 y=x的对称区域，f(x，y)为D上的连续函数，则

其中D1是D关于直线y=x对称的一半区域

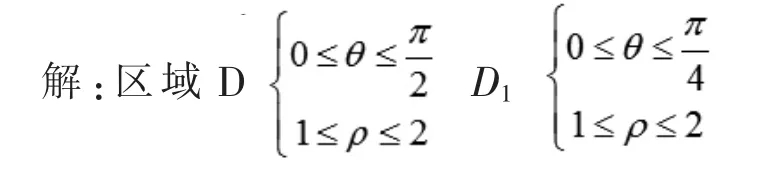
显然D是关于直y=x对称的区域，所以由（6）式可得

由以上讨论可知，对称区域上二重积分的计算，即使二元连续函数 f(x，y)不是关于 x和 y（或 x和y）的奇或偶函数，也有较简单的计算方法，并且包含了具有奇偶性的函数对称区域上二重积分的简化算法。比如当f(x，y)是关于x的奇函数时，即 f(-x，y)=-f(x，y)时，当积分区域 D 是关于 y轴的对称区域时，代入（2）式同样可得成立。所以应用本文给出的方法计算二重积分时，无需考虑二元连续函数的奇偶性，只要关注积分区域的对称性就可以了。当然，不是遇到所有对称区域上的二重积分计算时，都可以不加思索地盲目应用这里的计算方法。大家从以上例题可以看出，本文的方法主要起到了化简被积函数的作用，即通过函数相加计算后，使得被积函数更容易积分了，才能起到简化计算的目的。所以遇到对称区域上的二重积分计算时，先观察分析一下，如果此法把被积函数变得更难于积分了，该法就不可取。总之，上述方法应用得好，对于对称区域上二重积分的计算就会起到化繁为简、化难为易的重要作用，大大提高计算的速度和正确率。

[1]薛利敏.高等数学[M].北京：教育科学出版社，2016:124.