基于实测齿面的直齿锥齿轮有限元分析
李 枭 何 昕 曹雪梅
直齿锥齿轮的齿面为三维曲面,齿面修形以及机床加工中的误差都会影响到齿轮副的啮合性能。加工后直齿锥齿轮的齿面受到机床精度和热处理中轮齿变形等因素的影响,与理论设计齿面存在误差。由于实际齿面进行啮合性能分析是齿面制造数字化的关键环节,为此,国内外学者对此进行研究并取得了一定进展。文献[1]对锥齿轮仿真加工后的齿面进行NURBS曲面重构技术进行了探讨;文献[2]研究了准双曲面齿轮齿面参数化表示的方法;文献[3]提出了数字化齿面生成的方法。但是上述文献仅研究了理论齿面数字化重构的方法,而设计阶段所设计的理论齿面和实际加工出的齿面是有偏差的,在此基础上后续进行的分析也是有一定误差的,无法精确地得到实际齿面性能。
为分析加工后的齿面性能,本文通过实测齿面建立精确的齿轮三维有限元网格模型,在此基础上进行相应的齿轮有限元静力学分析,对分析直齿锥齿轮的齿面性能具有一定意义。
1.实测齿面拟合及曲率分析
1.1 实测齿面参数化拟合
通过在齿轮检测中心测量得到直齿锥齿轮的齿面点坐标值,根据实测点,以齿面拟合数学理论为基础,通过曲面重构技术构建锥齿轮的数字化齿面[4-5]。当曲面足够光滑,可以由多项式函数来近似表示,随着阶数提高,函数拟合值与实际值的偏差趋于零。测得曲面上一组离散点(xi,yi,zi),i=1,2…,n 的坐标, 可通过多项式来拟合该曲面,以三阶多项式为例,建立多项式过程如下。
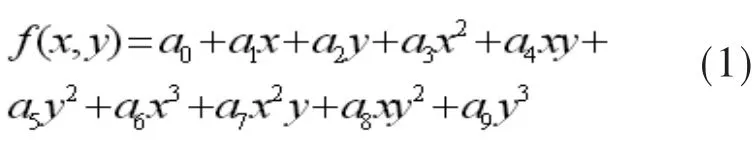
取曲面方程为 z=f(x,y),令 li=(xi,yi),li为曲面 上 测 得 点 坐 标 ,b(j),(l)为 拟 合 多 项 式 空 间 的 一组基。

则有:

式中 a1,a2,…,an为待定系数,拟合曲面是由取样值和实际的坐标值的差值平方和最小原理得到,这种方法不能保证每点都在拟合曲面上,假设计算偏差平方和为E(f),得:

要使E(f)达到最小,必须满足:

根据高斯消元法求得待定系数ai,可得到参数化拟合方程。
1.2 数值拟合曲面二阶拓扑结构分析
为了考量所设计的理论齿面在任意一点处的弯曲程度和弯曲方向,需要计算齿面的法曲率。齿轮齿面上任意一点有多个切方向,所以在任意方向上的弯曲型是不能量化的。本文通过Euler公式计算求解齿轮齿面上任意一点沿各个方向法曲率的变化规律,进而得到齿面法曲率的最大值和最小值,这个数值为齿面的主曲率。通过计算出的主曲率求出齿面的高斯曲率和平均曲率,得到齿面的拓扑结构。在参数化的齿轮齿面上任意齿面点P在任意方向(d)=du∶dv上法曲率kn为:

式(6)中,E,F,G 和 L,M,N 分别为曲面 S 的第一类基本变量和第二类基本变量。为计算齿面的法曲率kn的最值,设则有:

式(7)转化为求解二次分式的极值,有:
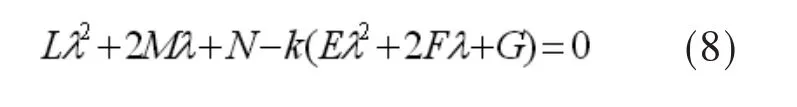
k1,k2(k1≤k2)是式(8)的两个根 ,由韦达定理得:
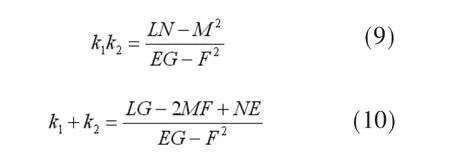
将 kn=k1,k2代入(7),解出两个根 λ2,λ1,得到达到最大值、最小值的方向。k1,k2之间的乘积为齿面在这一点的高斯曲率K:k=k1k2,高斯曲率的作用是描述齿面在任意一点处的弯曲程度。为了描述齿面在任意一点的平均弯曲强度,引入平均曲率H表达齿面在任意一点处平均弯曲程度。

由式(9)、(10)可以求解其值。
2.算例
2.1 齿面检测与五阶数字化重构
通过以上理论基础,进行直齿锥齿轮实测齿面实验,在齿轮检测中心实测直齿锥齿轮副的齿面,直齿锥齿轮副参数如表1示。

表1 直齿锥齿轮参数
本文使用德国克林贝尔P65齿轮检测中心对直齿锥齿轮副进行采样分析,以得到加工后实际齿面点坐标值。这种实测齿面考虑了加工误差及热处理变形等因素影响下产生的误差影响,更能实际的反映出齿面在工作中的性能。如图1所示齿轮检测中心[6-7]。

图1 齿轮检测中心
2.2 齿面拟合及拟合误差
对得到的实测齿面点进行齿面拟合,考虑到齿面拟合过程中会产生误差,所以在投影到同一平面中对应的点不可能完全重合。利用FORTRAN软件编程计算得到拟合误差,通过拟合实验可知:齿轮齿面拟合随着拟合阶数的增加,拟合精度也不断提高,如表2所示。在轮齿接触分析滚检齿面观察其接触区域时,齿面上涂抹的红丹粉厚度为6.35μm,本文拟合阶数达到五阶时,最大误差量为0.3μm,最大误差满足齿轮齿面研究精度要求,所以用五阶多项式进行齿轮齿面的拟合[8-9]。

表2 拟合误差
通过实验室齿轮检测中心采样齿面上45个离散点坐标,采用五阶多项式进行齿轮齿面的拟合。

拟合方程中的各阶系数如表3示。
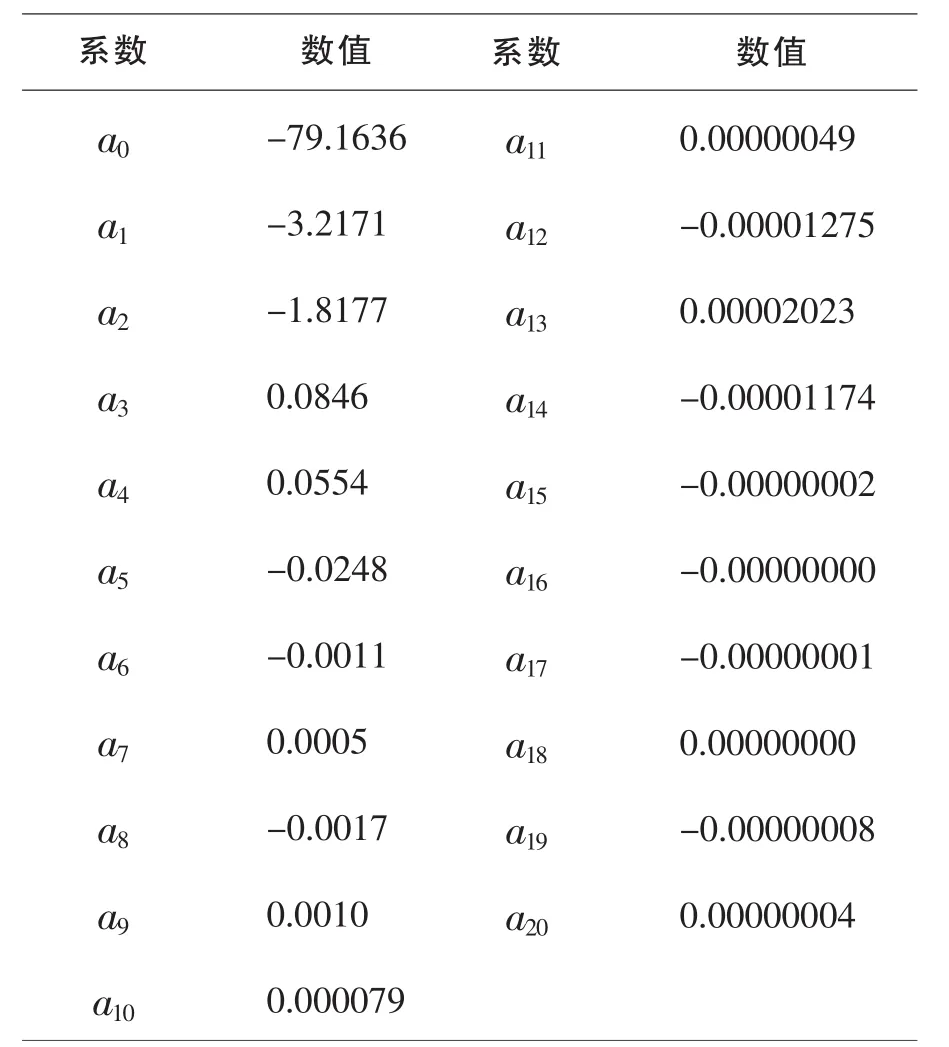
表3 各阶系数
2.3 映射网格划分
在齿面拟合过程中,标记点为节锥中点,这个点不是在测量齿厚的位置,为了保证齿厚,通过求解方程确保节锥线上中点锥距上y坐标为“0”,这样测量齿厚两个齿面节锥线上中点锥距处的点重合,再按照齿厚宽度旋转出轮齿厚度,如图2示。

图2 轮齿齿厚控制图
通过建立的齿厚控制图,可知通过拟合齿面旋转φ度后两齿面节锥线上中点锥距处点重合,旋转π/z角后生成轮齿齿厚。

2.4 有限元模型建立
根据建立的齿面拟合方程,依托旋转投影原理,对数字化齿面进行网格划分,构建精确的支持锥齿轮有限元模型[10-12]。单元类型选择六面体八节点单元,如图3所示,单元属性如表4示。

图3 实体单元SOLID45

表4 齿轮有限元单元属性
将节点和单元信息导入到ANSYS中进行齿轮齿面应力分析[13],如图4所示,直齿锥齿轮大轮全齿有限元模型。
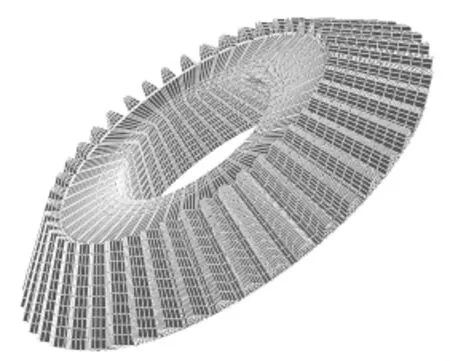
图4 直齿锥齿轮有限元模型
考虑到整个齿轮在ANSYS中导入节点过多,弯曲应力求解花费时间过长,并且在实际啮合过程中参与啮合的轮齿非常少,可以用边界条件约束来替代[14]。因此本次网格划分只选用三个齿进行受力分析,并且简化网格为沿着齿宽取9个节点。如图5所示单齿有限元模型。
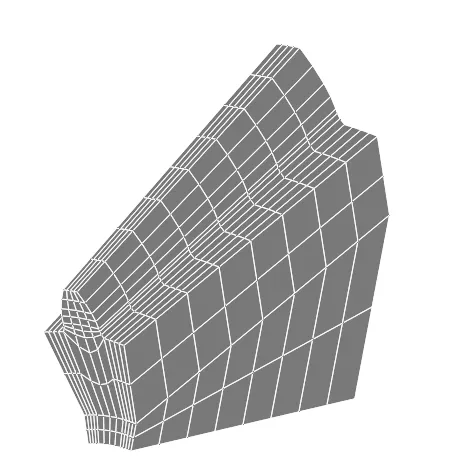
图5 单齿有限元模型
将直齿锥齿轮有限元模型面和其对称面、齿轮底面上的每一个节点限制6个自由度固定,确保齿轮完全固定。
2.5 载荷施加
齿轮在工作时,会在轮齿齿根位置产生齿根弯曲应力,在单对齿进入啮合时,在轮齿结合点处于单对齿啮合区最高点时,齿根所受到的弯曲应力最大。为了简化计算,便于在轮齿上施加载荷计算齿面应力,本文将载荷作用在轮齿的齿顶[15]。如图6所示为在三齿模型上的加载简图,载荷方向沿着齿顶圆法向压力角方向。

图6 加载简图
2.6 结果分析
对加载模型在ANSYS中求解,得到直齿锥齿轮大轮三齿模型的应力变形图,如图7所示。
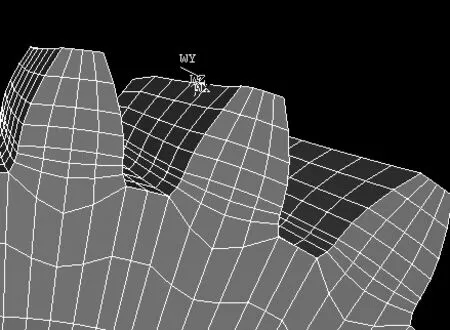
图7 应力变形图
从应力变形图中可以看出:轮齿有弯曲变形,在齿顶受力处等效应力最大,齿根处产生弯曲变形,齿根弯曲应力强度仅次于齿顶受力处。
3.结论
(1)对实测齿面点的拟合,拟合阶数越高,拟合曲面的误差就越小,精度越高,五阶拟合的精度满足齿轮研究的要求。
(2)对数字化齿面进行网格划分,构建精确的有限元模型。将节点和单元信息导入到ANSYS中进行齿面应力分析。这种针对实测齿面的力学分析考虑了加工误差及热处理变形带来的齿面误差,对指导实际加工具有重要的意义。
[1]李云松,阿达依·谢尔亚孜旦,丁撼.弧齿锥齿轮仿真加工齿面的NURBS重构及优化方法[J].机械传动,2016(2):39-43.
[2]苏智剑,吴序堂,毛世民,等.基于齿面参数化表示的准双曲面齿轮的设计[J].西安交通大学学报,2005(1):17-20.
[3]Wang Fulin,YiChuanyun,Wang Tao.eta1.A generating method fordigitalgeartooth surfaces [J].IntAdv Manuf Technol,2006(28):474-485.
[4]邢彬.螺旋锥齿轮齿面三坐标测量机测量关键技术与测量数据应用研究[D].长沙:中南大学,2010.
[5]刘光磊,常凯.弧齿锥齿轮高精度离散数值齿面啮合分析[J].航空发动机,2013(2):19-24.
[6]曹雪梅,王军,张海英.弧齿锥齿轮齿面误差检测与实验验证[J].中国 机 械工 程,2009,20(15):1799-1801.
[7]方宗德,曹雪梅.航空弧齿锥齿轮齿面坐标测量的数据处理[J].航空 学 报,2007,28(2):456-459.
[8]韩佳颖,王太勇,李清,等.准双曲面齿轮切削仿真及齿面误差分析[J].制造技术与机床,2010(1):112-116.
[9]徐爱军,邓效忠,张静,等.准双曲面齿轮振动噪声试验与预估分析研究[J].机械设计,2012(12):17-21.
[10]叶先磊,史亚杰.ANSYS工程分析软件应用实例分析[M].北京:清华大学出版社,2003.
[11]赵葵,刘海岷,雷海胜,等.基于 ANSYS Workbench的蜗杆斜齿轮静力学仿真[J].武汉工业学院学报,2012(1):28-31.
[12]唐进元,刘艳平.直齿面齿轮加载啮合有限元仿真分析[J].机械工程学报,2012(5):124-131.
[13]娄佳佳.基于安装误差敏感性的直齿锥齿轮齿面设计与实验分析[D].洛阳:河南科技大学,2014.
[14]蓝娆,杨良勇,罗昌贤.基于 ANSYSWORKBENCH的齿轮接触应力分析[J].中国新技术新产品,2011(15):1.
[15]李小清,周云飞,王延忠,等.螺旋锥齿轮拟合齿面啮合特性分析方法[J].中国机械工程,2003(13):65-69.

