力学中求解约束力的方法解析

秦 静 赵恒博

(青岛理工大学琴岛学院，山东 青岛 266106)

力学是七大基础学科之一，力学的应用无处不在，在我们的日常生活中和国防领域以及航天航空领域有着不可替代的作用[1-3]。对于土建类专业的学生来说，力学是非常重要的专业基础课，主要开设三大力学：理论力学、材料力学和结构力学。力学是土建类专业学生学习专业课程的基础，也是将来解决工程实际问题的理论基础[4]。而在三大力学中求解约束力是一个非常重要的基本内容，可以说是学生学习力学的基本功，在三大力学中都有讲解求约束力的方法，各有特点和用途，在文中我们分别举例说明求约束力的方法，并比较它们的特点和不同。

1.方法介绍与数值算例

1.1 利用静力平衡方程求约束力

静力平衡方程求约束力是三大力学中最基本、最常用的一种方法，当物体系统受平衡力系时，就可以通过列静力平衡方程对未知的约束力进行求解。静力平衡方程有三种，一种是投影方程，是研究对象中所受的所有力及力偶在某个方向坐标轴的投影代数和等于零；一种是力矩方程，是研究对象上所受的力及力偶对平面内某点取矩的代数和等于零；第三种是力偶矩平衡方程。在平衡的力偶系中，所有力偶的力偶矩代数和等于零[5]。此方法通俗易懂、容易掌握、求解迅速、不易出错。下面我们举例说明。

例：求如图1静定多跨梁中支座D的约束力。

图1

解：①画层次图如图2。AB杆和DE杆为基本部分，BC杆为附属部分。

图2 层次图

②取BC杆受力如图3，通过列力偶矩平衡方程求出FC。

图3 BC杆的受力图

③列虚功方程，结构上作用的所有的力在其位移上所做的虚功之和为零。取CE杆受力如图4，列对E取矩的力矩方程求出 FD。

图4 DE杆的受力图

解得：FD=40kN(↑)

1.2 利用虚功原理求约束力

刚体系统的虚功原理是指：刚体体系在任意平衡力系作用下，体系上所有主动力在任一与约束条件相符合的无限小刚体位移上所做的虚功总和恒等于零，其特点是用几何方法求解静力学问题。现举例如下。

如图5静定多跨梁，试用虚功原理求支座D处的约束力。

图5

解：①将力偶还原为两个集中力，如图6，A和E处的两个大小为1KN集中力。

图6

②解除支座B代以约束力FB，并沿约束力正向产生单位线位移，如图7为结构的位移图。

图7 解除后FB的位移图

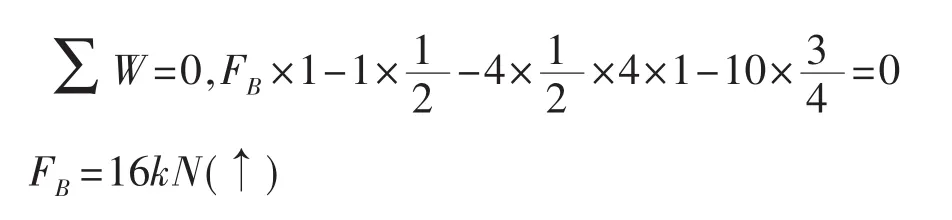
1.3 利用影响线求约束力

影响线是指在单位移动荷载作用下，结构的约束力或内力等物理量随荷载位置变化的规律曲线[7]。影响线在力学中一个很重要的应用就是求约束力。其求解约束力的规律如下。

（2）均布荷载作用时：FA=q·A(q 为均布荷载的荷载集度；A为均布荷载所对应的FA影响线中的面积，其面积在基线上侧为正，下侧为负。)

（3）集中力偶作用时：先将力偶还原为两个等值反向的集中力，然后按照集中荷载求解约束力的方法进行求解，注意集中力方向向下为正，向上为负。

例：利用影响线求出图8所示梁中B处的约束力。

图8

①首先还原力偶为两个集中力表示，如图9所示两个大小为6kN的集中力。

图9

②画出FB的影响线，如图10所示。

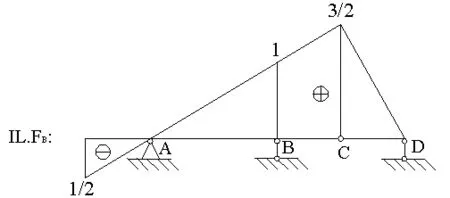
图10 FB的影响线

③利用影响线中荷载对应数值列出表达式为：

1.4 利用力法求超静定结构的约束力

力法是以多余未知力作为基本未知量，解除多余约束代以约束力得基本体系，并根据基本体系与原体系变形协调的位移条件求解基本未知量的方法[8]。现举例如下。

例：求图11示超静定梁C处的约束力。

图11

解：①解除C处的支座，代以约束力FC，得基本体系，如图12。

图12

②写力法的基本方程：δ11FC+△1p=0

③作 Mp图和图求 δ11和△1p

Mp图为实际荷载作用下基本体系的弯矩图，如图13；图为当FC=1时单位荷载作用下基本体系的弯矩图，如图 14。δ11通过图的自乘来求解，△1p通过 Mp图和图相乘得到。

图13

图14

④将δ11和△1p带入力法的基本方程求出FC。

力法是求解超静定结构约束力的基本方法。它解除了多余约束把超静定结构转化成静定结构，利用位移条件建立方程求出约束力。

2.结论

求解约束力是三大力学中一个基本而重要的知识点，文中通过静力平衡方程、虚功原理以及影响线求解了静定结构的约束力。静力平衡方程法是基本方法，通俗易掌握，学生需正确列出平衡方程进行求解；虚功原理法从功的角度列虚功方程进行求解，难点是找出各量的几何关系；利用影响线求约束力，形象直观，难点是需首先正确画出结构的影响线。力法是一种求解超静定结构约束力的方法，它将超静定结构转化为静定结构进行求解，是一种行之有效的好方法。

[1]越桂杰，魏伟，谷莉，等.工程力学教学中的一些教学和工程实例[J].力学与实践，2012，34（2）：83-84.

[2]宁交贤.从几个国防课题看力学实验在航空工程研究中的优势和重要作用[C]//首届全国航空航天领域中的力学问题学术研讨会论文集（下册），2004：143-147.

[3]孟光，周徐斌，苗军.航天重大工程中的力学问题[J].力学进展，2016，46(6)：267-322.

[4]叶志明，刘邵峰.复合材料-土建结构的力学性能和加固技术[J].力学与实践，2001，23（3）：76-79.

[5]哈尔滨工业大学理论力学教研室.理论力学（I）:第 7版[M].北京：高等教育出版社，2010：37-45.

[6]龙驭球，包世华，袁驷.结构力学（I）:第 3 版[M].北京 ：高 等教育出版社，2012：80.

[7]洪范文.结构力学:第 5版[M].北京：高等教育出版社，2013：182.

[8]李全旺.结构力学[M].天津：天津科学技术出版社，2014：102-104.