二维非凸孔型单相声子晶体带隙研究

许卫锴，张 蒙，宁金英(沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136)

近年来，声波和弹性波在周期性复合材料中的传播越来越受到关注。相比光子晶体[1]，声子晶体是由一种弹性常数及密度周期分布的新型功能材料，当弹性波在声子晶体内部传播时,受其周期性结构的影响,在一定频率范围(禁带)内，弹性波会被禁止传播，而在其他频率范围(通带)内，弹性波可以无损耗地传播[2]。因此，在噪声隔离和振动控制等方面声子晶体具有潜在的应用前景，尤其在隔振方面，它可以完成常规阻尼难以完成的任务，为超精加工、精密仪器等在一定频率范围内提供无振动的环境。因此，在Kushwaha等人[3]提出了声子晶体的概念后，研究人员开始广泛关注这种周期性介质对波的传播行为的影响[4-7]，随后出现了许多新型的人造结构的声子晶体[8-10]。此外，在国防工业方面它也有巨大的应用潜力[11-12]。

到目前为止，声子晶体产生带隙的机理大体分为两种:Bragg 散射型和局域共振型。在Bragg 散射型声子晶体中，带隙主要与结构的物理参数、周期性等结构参数有关[13]，当入射弹性波的波长与声子晶体的晶格尺寸相近时弹性波将受到结构强烈的散射作用，使得带隙频率对应的波长与晶格尺寸处于同一数量级；而在局域共振型声子晶体中，虽然结构的物理参数也有一定影响，但带隙主要由晶体中散射体的共振产生。2000年，刘正猷等[14]首次提出了局域共振型声子晶体的概念，他们在环氧树脂的基体中嵌入以硅橡胶包裹的铅球的共振单元并对此进行了相应的实验。由于引进了共振单元，第一带隙频率大大降低，比同样晶格尺寸的 Bragg 散射型声子晶体产生的带隙低了两个数量级，但大部分的共振型声子晶体只能在低频范围内产生较窄的带隙。因此，为了在低频范围内获得较宽的带隙，许多研究人员开始提出板状、梁状等结构形式的声子晶体,如三明治板的板状体系[15]含有共振体梁的梁式体系[16]。周期性孔型声子晶体具有质量较轻且制作简单的优点，在近年来受到了越来越多的关注。本文研究了一种含非凸型孔的二维单相声子晶体，并讨论了结构几何参数对带隙的影响，这些结果为声子晶体的设计提供了一定的参考依据。

1 理论方法

对于线弹性、小变形、各向异性、无阻尼且无源的非均匀介质，角频率为ω的谐振弹性波在其中的传播行为可以用以下波动方程描述[17-18]

-ρ(r)ω2u(r)=·(C(r):u(r))

(1)

-ρ(r)ω2ui=T·[C44(r)Tui]+T·uT]+[(C11(r)-2C44(r))TuT],i=x,y

(2)

-ρ(r)ω2uz=·(C44(r)uz)

(3)

根据Bloch定理，声子晶体的中位移场u(r)可以表示成

u(r)=ei(k·r)uk(r)

(4)

其中，uk(r)是单胞内的位移场，与结构有相同的周期性，k=(kx,ky)被限定在第一布里渊区内。利用有限元软件求解时，可以在一个单胞内进行，单胞内离散形式的特征方程为

(K-ω2M)U=0

(5)

其中，U是节点位移，K与M分别是刚度矩阵和质量矩阵。

当单胞边界满足Bloch周期条件时，则结构内的每个点都将满足Bloch条件[19]。将Bloch定理沿着周期方向施加在单胞边界上时，单胞边界条件变为

U(r+a)=ei(k·a)U(r)

(6)

其中，a为声子晶体的格矢基矢量。将波矢k沿着结构的不可约布里渊区的高对称边界扫描，通过求解特征值即可得到能带结构。

本文采用有限元软件Comsol Multiphysics5.2a对一种新型的二维非凸孔型声子晶体进行仿真计算，其中平面混合模态和剪切模态可分别采用固体力学模块和压力声学模块进行求解[18]。通过施加Floquet周期边界条件，计算能带结构的问题就转化为一个特征值问题。

2 数值计算与分析

2.1 计算模型

研究表明，对于由均匀固体周期开孔得到的多孔型声子晶体，孔的形状几乎是唯一可以调控带隙的参数[18]，因此研究开孔形状及其尺寸对系统带隙特性的影响具有十分重要的意义。一般来说，含非凸型截面孔的声子晶体较凸型孔更容易在较低频率产生较宽的完全带隙[18]。例如，甄妮等人[20]研究了含正方形、三角形以及六角蜂窝结构的周期多孔材料，结果表明仅存在方向带隙而无完全带隙。Su等人[21]讨论了含圆形孔、旋转方孔和六角形孔声子晶体的带隙特性，结果表明不同形状的孔具有不同的带隙特性。图1(a)和1(b)分别显示了方形孔和圆形孔的能带图，其中b为方形孔边长，R为圆形孔半径。可以看出，方形孔并不存在完全带隙，而圆形孔可以产生相对较窄的禁带。在方形边框上附加半圆形凸起时，此时孔的形状将变为一个类似“X”变形体的非凸型截面，如图2(a)所示，其中晶格常数为a，边框宽度为t，半圆的半径为r。对于方形晶格来说，其不可约布里渊区的高对称边界为Γ-Χ-Μ-Γ，如图2(b)所示。当选取合适的尺寸参数时，单元将会发生局域共振并产生较大的带隙，如图1(c)所示。

图1 不同形状的声子晶体能带结构

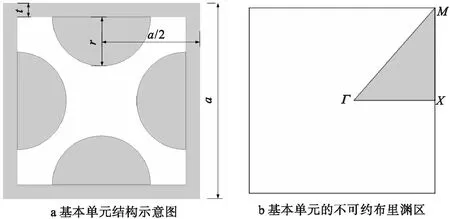
图2 非凸型单相声子晶体示意图

本文采用铝为基体材料，晶格常数a为0.01 m，其材料属性中密度ρ=2 700 kg/m3，杨氏模量E=20 GPa，泊松比υ=0.25。计算得到结构的能带如图3所示，纵坐标采用归一化频率Ω=fa/ct，其中f为频率，ct=1 721 m/s为基体的横波波速，图中实线和虚线分别表示声子晶体的混合模态和剪切模态。

2.2 半圆半径影响

图3显示了当边框宽度t为0.000 3 m时，不同的半圆半径对带隙分布的影响。可以发现，当取半圆半径r为0.001 m时，在归一化频率0.82、1.4和1.65附近存在三条较明显的带隙，并在频率1.17处存在一条极细的带隙，更低的频率则不存在完全带隙；调整半圆的半径r为0.001 5 m时剪切模态的第7条能带下降，使得原来1.6<Ω<1.7范围的带隙切割为两条，且带宽较之前有所增加;同时，由于混合模态的第11条能带大幅上升，原来0.82频率处的带宽大幅增加，位于1.17处的极细带隙的带宽也大幅增加，在更低的频率0.5和0.61范围处也打开两条带隙；当半径r为0.002 m时在频率为1.9的位置出现一条带隙，同时，由于剪切模态的第7、8条能带继续下降，第6能带则上升，使得原来频率1.6处的两条带隙中较宽一条变得极细，而原本较细的一条则完全消失，由于混合模态第7-12条能带上升，使得1.2处的带隙消失，0.8<Ω<0.98处的带隙上升至1<Ω<1.7，而0.83<Ω<0.97处出现另一条新带隙，频率0.6处的带隙也上升至0.7处。另外，由于混合模态第6条能带下降，原本0.5处的带隙增大为0.4<Ω<0.61的宽带隙；当半圆的半径r为0.002 5 m时，由于混合模态第7-12条能带继续上升，且第13条能带下降，以及剪切模态第3条能带上升，第4能带下降，原本1<Ω<1.7和0.83<Ω<0.97处的两条带隙有小幅度上升，且带宽同时变小，频率1.58处也出现一条带隙。另外，由于混合模态第6条能带继续下降，0.4<Ω<0.61处的带隙进一步增大为0.38<Ω<0.79；当半圆的半径r为0.003 m时，由于混合模态第7-12条能带大幅上升，且第13条能带大幅下降，原本1<Ω<1.7和0.83<Ω<0.97处的两条带隙消失，而在频率为1.36和1.39处出现两条极细带隙，在频率为1.7处出现一条稍宽带隙，另外，由于混合模态的第6能带小幅下降，剪切模态的第3条能带小幅上升，使得0.38<Ω<0.79处的带隙增大为0.36<Ω<0.81。

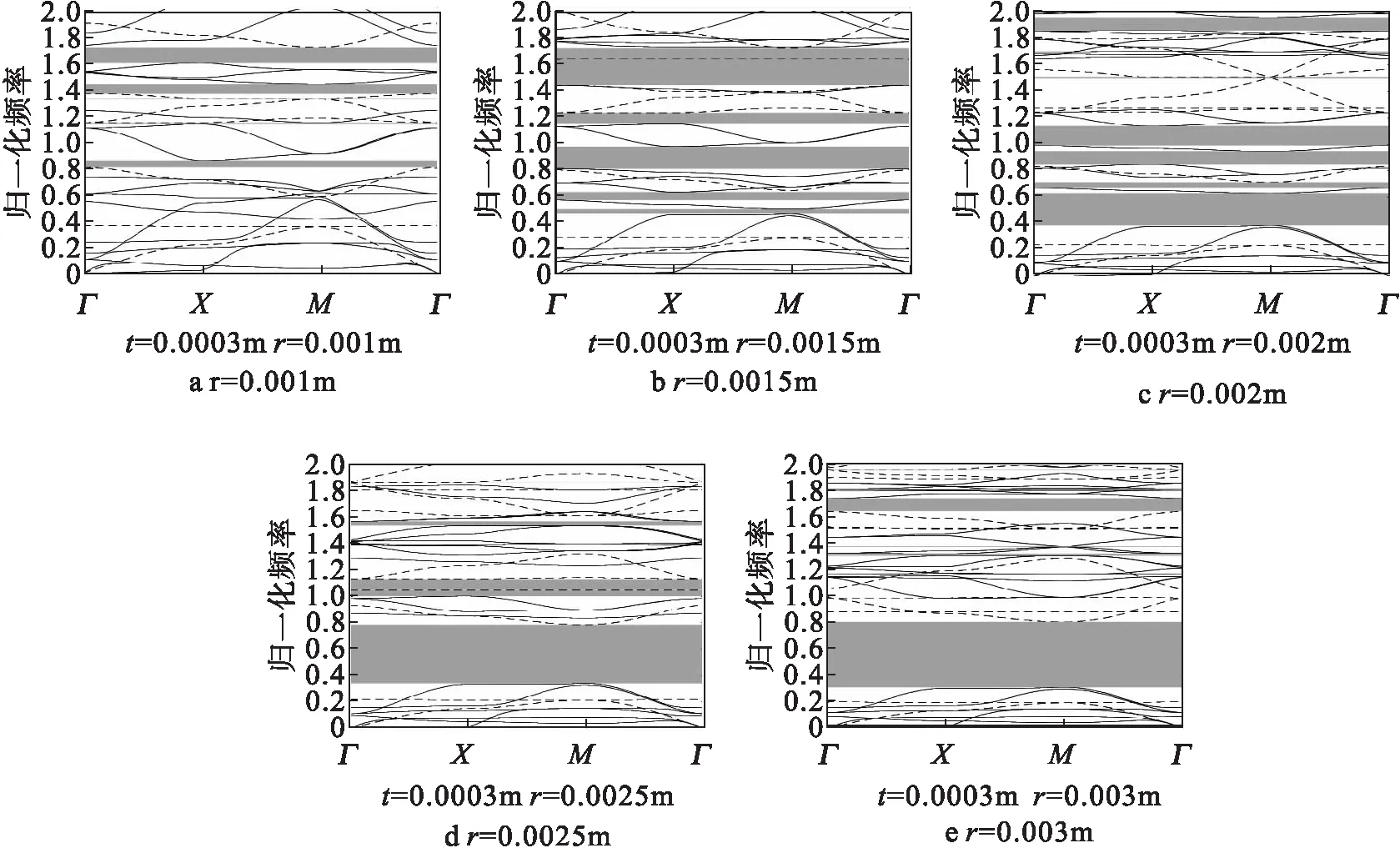
图3 不同半径的能带结构实线和虚线分别代表混合模态和剪切模态

图4 低频带隙边界随半圆半径变化情况

另一方面，由图3可知，低频带隙一般出现在混合模态的第6、7条能带与剪切模态的第2、3条能带之间，因此我们着重讨论这四条能带随半圆半径变化情况。图4显示了低频带隙的边界随半圆半径的变化情况，其中，混合模态与剪切模态分别用“○”和“*”标记，实线为混合模态第7(或剪切模态第3)能带的下边界，虚线为混合模态第6(或剪切模态第2)能带的上边界。只有高阶能带的下边界高于低阶能带的上边界时才会产生带隙。从图4可以看出，当半圆半径取0.001 m时，由于混合模态第6条能带的上边界高于在第7条能带的下边界，因此并未产生完全带隙，这也与图3(a)的结果相吻合。当半圆半径增大到0.001 5 m时开始出现完全带隙，随着半圆半径继续增大，低频完全带隙也逐渐变宽，如图4中阴影部分所示。

为了更好地观察构型尺寸对带隙宽度及位置的影响，本文引入低频相对带宽[18]和总体绝对带宽[22]两种指标对构型进行评价。其中，低频相对带宽考虑第一个禁带带宽尽可能大的情况下频率尽可能低，总体绝对带宽则考虑在一定频率范围内所有禁带的总体宽度。低频相对带宽和总体绝对带宽的目标函数如式(7)和式(8)所示。

(7)

(8)

计算结果如表1所示。结合图3、图4可以看出，当改变半圆的半径时，无论是混合模态还是剪切模态，其能带变化都较为明显。从总体绝对带隙来看，当半径为0.001 m时禁带带宽较小仅为12.3%，但增大半径到0.001 5 m后总体绝对带宽迅速增大到31.7%。尽管进一步增大半径并不能带来绝对带隙的扩宽，但会导致带隙的频率下移，从而使得低频相对带宽逐渐增大，因此，较大的半圆半径成为更优的选择。然而，由于继续增大半圆半径在系统发生振动变形时内部半圆会发生挤压，因此在本文下一部分中取半径为0.003 m进行分析。

2.3 边框宽度影响

图5显示了半径r为0.003 m时不同的边框宽度对带隙分布的影响。可以看出，对比边框宽度t为0.000 5 m的情况，取t为0.000 4 m时,混合模态的第6条能带略有下降，剪切模态的第3条能带略有上升，使得第一条带隙宽度略微增大；当取t为0.000 3 m时混合模态的第6条能带下降较明显，剪切模态的第3条能带依然有部分上升，使得第一条带隙宽度扩大为0.32<Ω<0.8；当取t为0.000 2 m时,混合模态的第6能带继续下降，剪切模态的第3条能带则继续上升，第一条带隙宽度扩大为0.28<Ω<0.82；当取t为0.000 1 m时，混合模态的第6能带虽然有大幅下降，但第7条能带则有更大幅度下降，第8、9、10条能带也有较大幅度下降，因此，第一条带隙被切割为两条完全带隙，两条带隙宽度分别为0.21<Ω<0.51和0.54<Ω<0.77。同时，在高频范围内也出现两条新的完全带隙，其宽度分别为0.99<Ω<1.2和1.27<Ω<1.38，但带隙宽度较小。

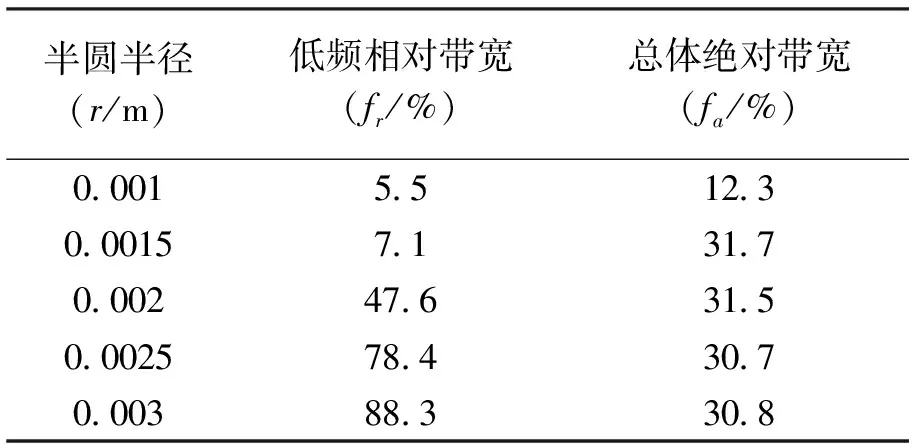
表1 半圆半径对带隙宽度及位置的影响情况

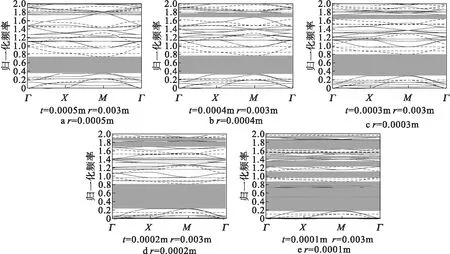
图5 不同边框宽度的能带结构(注：实线和虚线分别代表混合模态和剪切模态)

图6显示了低频带隙的边界随边框宽度的变化情况，同样，混合模态与剪切模态分别用“○”和“*”标记，实线为混合模态第7(或剪切模态第3)能带的下边界，虚线为混合模态第6(或剪切模态第2)能带的上边界。可以看出，随着边框宽度的减小，低频完全带隙逐渐增大，并在0.000 2 m附近时取得最大。当边框宽度进一步减小到0.000 1 m时低频完全带隙再次减小，如阴影部分所示。

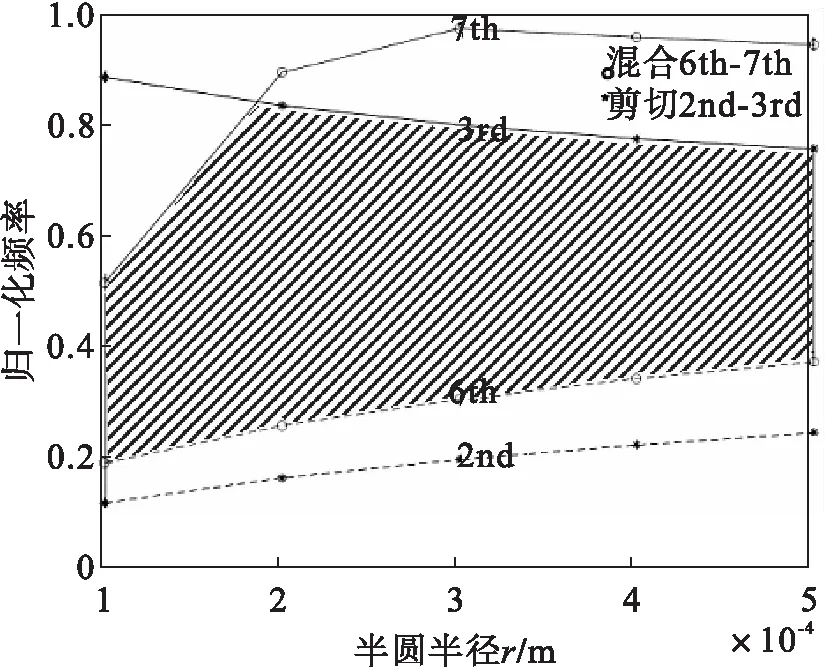
图6 低频带隙边界随边框宽度变化情况

同样的，我们分别计算了不同边框宽度下的低频相对带宽和总体绝对带宽，如表2所示。可以看出，随着宽度的不断减小混合模态的能带依然受到较大影响，低频相对带宽呈逐渐增大趋势，当框架厚度为0.000 1 m时低频相对带宽率减小，这是由于混合模态第7条能带下降过快，低频带隙被切割为两条相对较窄的完全带隙造成的，但总体绝对带宽则一直呈现逐渐增大趋势，由于继续减小框架宽度会在材料制备上存在一定难度，因此不再继续减小框架宽度。

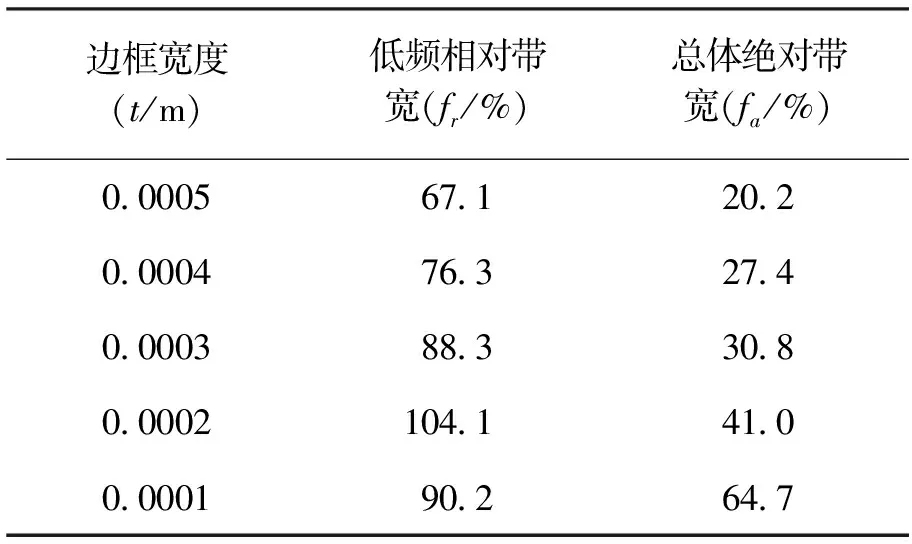
表2 边框宽度对带隙宽度及位置的影响情况

3 结论

本文基于局域共振型声子晶体结构，对一种新型的二维含非凸型孔声子晶体构型的带隙特性进行了分析和研究，并讨论了结构几何参数对带隙性质的影响。结果表明，结构几何参数对系统的带隙特性具有显著的影响，而合理确定几何参数可使该新型声子晶体在低频范围内打开相对较宽的完全带隙，这为声子晶体的带隙设计提供了一定的理论依据。

[1] John S.Strong localization of photons in certain disordered dielectric superlattices[J].Physical Review Letters,1987,58:2486-2489.

[2] 温熙森,温激鸿,郁殿龙,等.声子晶体[M].北京:国防工业出版社,2009.

[3] KUSHWAHA M S,HALEVI P,DOBRZYNSKI L,et al.Acoustic band structure of periodic elastic composites[J].Physical Review Letters,1993,71:2022-2025.

[4] WANG Y S,ZHANG C Z.Bandgaps and directional propagation of elastic waves in 2D square zigzag lattice structures[J].Journal of Physics D:Applied Physics,2014,47:485102.

[5] WEN J H,YU D L,WANG G,et al.The directional propagation characteristic of elastic wave in two-dimensional thin plate phononic crystals[J].Physics Letters A,2007,364:323-328.

[6] LI J,WU F G,ZHONG H L,et al.Tuning the acoustic directional radiation by rotating square rods in two-dimensional phononic crystals[J].Modern Physics Letters B,2014,28(23):1450187.

[7] WANG Y F,WANG Y S,ZHANG C Z.Bandgaps and directional properties of two-dimensional square beam-like zigzag lattices[J].AIP Advances,2014,4(12)：2022.

[8] WANG P,SHIM J,BERTOLDI K.Effects of geometric and material nonlinearities on tunable bandgaps and low-frequency directionality of phononic crystals[J].Physical Review B,2013,88(1):2466-2472.

[9] 陈阿丽.随机失谐和准周期声子晶体中弹性波传播特性研究[D].北京：北京交通大学,2008.

[10]DAVIS B L,HUSSEIN M I.Nanophononic metamaterial:Thermal conductivity reduction by local resonance[J].Physical Review Letters,2014,112(5):055505.

[11]张荣英,姜根山,王璋奇,等.声子晶体的研究进展及应用前景[J].声学技术,2006,25(1):35-42.

[12]徐记伟,张政,黄勇,等.周期性结构材料在隐身中的应用[J].工艺与材料,2009(4):57-61.

[13]赵宏刚,韩小云,温激鸿,等.新型声学功能材料-声子晶体.材料科学与工程学报,2003,21(1):153-156.

[14]LIU Z Y,ZHANG X X,MAO Y W,et al.Locally resonant sonic materials[J].Science,2000,289(5485):1734-1736.

[15]CHEN J,SUN C.Wave propagation in sandwich structure with resonators and periodic cores[J].Journal of Sandwich Structure and Materials,2013,15(3):359-374.

[16]HAN X Y,WEN J H,WEN X S.Flexural wave band gaps in locally resonant thin plates with periodically attached spring-mass resonators[J].Journal of Physics D:Applied Physics,2012,45(19):195401.

[17]柯佼.含共振单元的二维多孔声子晶体带隙特性研究[D].北京:北京交通大学,2012.

[18]王艳锋.含共振单元声子晶体的带隙特性及设计[D].北京:北京交通大学,2015.

[19]LI J B,WANG Y S,ZHANG C Z.Dispersion relations of a periodic array of fluid-filled holes embedded in an clastic solid[J].Journal of Computational Acoustics,2012,20(4):1250014.

[20]甄妮,闫志忠,汪越胜.蜂窝材料的弹性波传播特性[J].力学学报,2008,40(6):769-775.

[21]SU X X,WANG Y F,WANG Y S.Effects of poisson’s ratio on the band gaps and defect states in two-dimensional vacuum/solid porous phononic crystals[J].Ultrasonics,2012,52:255-265.

[22]XU W K,WANG W.Pareto optimal design of layered bandgap materials with multiphase microstructures using evolutionary algorithms[J].Applied Acoustics,2016,102:133-136.