基于非误差建模的高动态GNSS矢量跟踪环路
金 天,杜 越,王晨炎
(北京航空航天大学,北京 100191)
0 引言
随着航空航天技术的发展,矢量多通道联合跟踪因为具有高动态、高灵敏度、抗干扰等优点而受到广泛关注。在传统环路中,各通道对卫星信号的跟踪是相互独立的,不同卫星信号的相关性被忽略,导致信息没有得到充分的利用。矢量算法通过对接收机、卫星位置几何分布信息的利用,将多通道信号的融合滤波与定位解算相结合,提高了接收机的整体工作性能[1-2]。文献[3]介绍了一种建模方法,通过对载体位置、速度进行误差状态量建模,实现对载体位置、速度的定位解算。该模型下,载体加速运动会导致载波环路产生动态应力误差[4]。本文针对此问题,提出了基于非误差建模的高动态GNSS矢量跟踪环路。
1 传统矢量跟踪算法
传统矢量跟踪环路算法结构如图1所示。首先将各个通道的码鉴别器和载波鉴别器输出转化为伪距、伪距率,作为量测量用于环路滤波,然后将滤波得到的伪距、伪距率误差转化为码环、载波误差,对各个通道的跟踪环路进行调整。
传统矢量模型为误差状态量建模,状态量中的各个维度分别表示对应的误差。状态量可表示为Xk=[δx,δvx,δy,δvy,δz,δvz,δt,δf]T。其中,δx,δy,δz为载体的位置误差,δvx,δvy,δvz为载体的速度误差,δt,δf为时钟误差和时钟频率误差。
在误差状态量模型中,由于k-1时刻的状态量误差已得到修正,k时刻的状态量误差预测为零,所以k时刻状态量预测值为Xk|k-1=[0,0,0,0,0,0,0,0]T[5]。
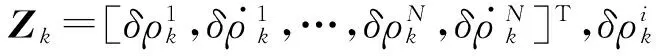
通过状态估计方程,可以求得k时刻的状态量估计值Xk。
Xk=Xk|k-1+Kk[Zk-HkXk|k-1]
(1)
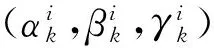
(2)
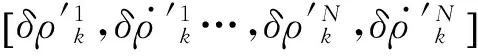
Yk=HkXk
(3)
将卫星伪距、伪距率误差Yk转化成环路的码片、载波误差,即可对数字控制振荡器(NCO)进行修正。
2 非误差建模的矢量跟踪算法
在传统矢量跟踪算法中,模型状态量包括载体的位置和速度,缺少更高的动态维度。原因是在误差状态量模型中,状态量的维度是由量测量决定的,没有更高阶的量测量,就难以对载体更高阶的运动状态建模。传统建模方法的滤波回路如图2所示[6]。
本文采用了一种新的建模方式,在误差状态量模型的基础上增加非误差状态量,将状态量写为X′=[δx,δvx,ax,δy,δvy,ay,δz,δvz,az,δt,δf]T,其中ax,ay,az表示载体的加速度,为非误差状态量。
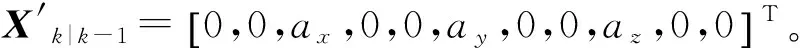
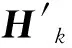
(4)
根据文献[3]所述,载体动态和滤波观测量是与当前的状态估计是线性相关的。因此载波环路的加速度动态应力误差可以直接通过状态量计算。在公式的基础上,加入对加速度动态应力误差的修正,设T为相干积分时间,载波环路的误差为:
(5)
新的滤波回路如图3所示。
与图2相比,误差与非误差建模相结合的矢量跟踪算法有如下改变:1)状态量在位置误差、速度误差的基础上增加了载体加速度维度;2)状态量预测需要对误差量清零,且保持非误差量的不变;3)载波环路的误差计算加入了载体加速度的动态应力误差。
在传统矢量环路中,状态量模型只考虑到速度维度,加速度作为动态应力误差包含在环路误差中,需要载波鉴别器进行误差的反馈[4]。在新的矢量环路中,载体加速度通过状态量得到估计,并对环路进行反馈修正,此时环路的动态应力误差只包含更高阶动态维度的误差。通过这种方法降低了环路的动态应力误差,使载波环路更难到达鉴别器的跟踪门限,从而提高环路的动态性能。
3 仿真测试
采用GNSS中频信号模拟器产生GPS L1频点仿真数据对本文提出的矢量跟踪环进行仿真分析和验证。仿真的基本参数设置为:数字载波中频为4.17 MHz,采样频率为12 MHz,对10颗卫星进行仿真,卫星号(PRN)分别为3,7,13,15,16,19,21,23,25,27,信号的初始载噪比为50 dB,相干积分时间为10 ms。
3.1 静态测试
静态测试仿真时长200 s,在100 s后每2 s增加1 dB的白噪声,以测试接收机的灵敏度性能。
静态测试结果如下,环路误差及失锁门限数据见表1,码环误差、载波误差、位置误差分别见图4、图5、图6。由测试结果可知,新算法的码环误差和载波误差与传统矢量算法性能基本一致。在失锁结果上,二者的失锁门限均为载噪比22 dB。
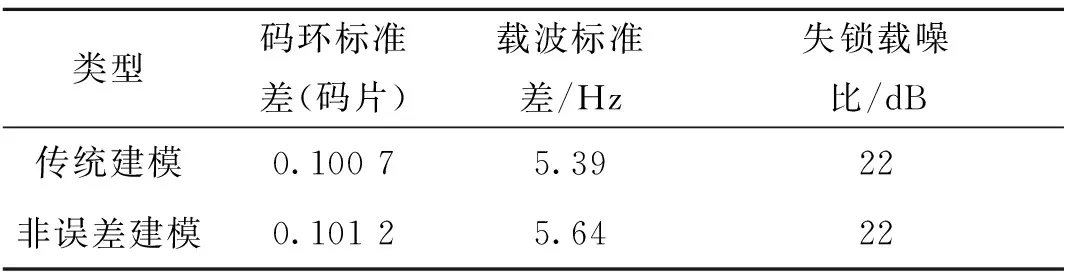
表1 静态测试环路误差及失锁门限(PRN=3)
3.2 动态测试
动态测试仿真时长为300 s,载体的速度、加速度如图7所示。仿真开始时载体保持静止,从100 s开始载体进行往返运动,每往返一次,加速度绝对值增加10g,加加速度50g/s,运行到300 s时载体加速度为200g。高动态的仿真能够对环路的极限性能进行测试,进而比较两种建模方式的动态性能。
动态测试结果中,环路误差及失锁门限数据见表2,码环误差、载波误差、位置误差分别见图8、图9、图10。由测试结果可知,高阶矢量算法可以跟踪加速度200g的载体,而传统矢量算法在载体加速度30g时就已经失锁。定位精度上,新算法的定位误差始终保持在15 m以内,而传统矢量算法在130 s后就因为环路失锁导致了定位结果的发散。
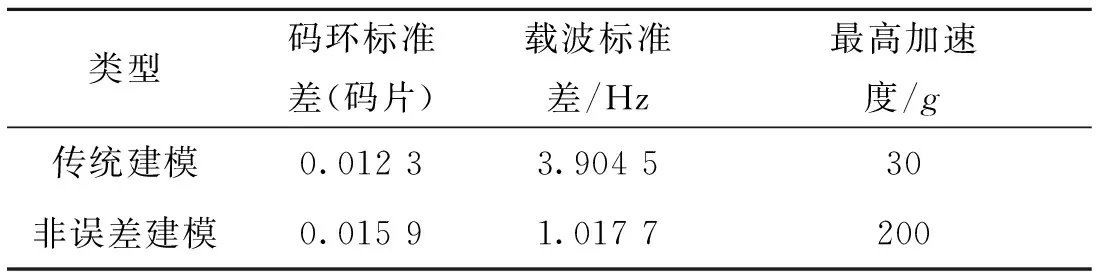
表2 动态测试环路误差及失锁门限(PRN=3)
仿真结果表明,非误差建模的矢量跟踪算法可以准确的估算载体的加速度。通过消除载波环路动态应力误差中的加速度分量,降低了环路误差,从而提高了环路的动态性能。
4 结论
本文提出了基于非误差建模的高动态GNSS矢量跟踪环路。该环路对载体加速度采用非误差状态量建模方式进行估计,消除了载波环路动态应力误差中的加速度分量。仿真测试结果表明,该环路能够在不影响接收机灵敏度的情况下,实现对更高动态载体的跟踪。
[1]Sennott J W, Senffner D. Navigation receiver with coupled signal-tracking channels: US 5 343 209[P]. 1994-8-30.
[2]Kim K, Song J, Jee G, et al. The adaptive vector tracking loop design for high dynamic situations[C]//Proceedings of ENC GNSS 2008. Naplas: 2008.
[3]Lashley M. Modeling and performance analysis of GPS vector tracking algorithms[D]. US: Auburn Unversity, 2009.
[4]Lashley M, Bevly D M, Hung J Y. Performance analysis of vector tracking algorithms for weak GPS signals in high dynamics[J]. IEEE Journal of selected topics in signal processing, 2009, 3(4): 668-669.
[5]Bhattacharyya S. Performance and Integrity Analysis of the Vector Tracking Architecture of GNSS Receivers[D]. US: Universit of Minnesota, 2012.
[6]秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,1998.

