隐身飞机随队干扰对雷达探测性能的影响
刘占强,梁路江,王春阳
(空军工程大学防空反导学院,陕西 西安 710051)
0 引言
隐身战机要完成作战任务,需具备一定的突防生存力,主要凭借独特的隐身优势和较强的电子战能力。目前,该领域的专家、学者主要利用飞机姿态变化与静态RCS相结合的方式,对目标动态RCS的分布特性[1-4]展开研究,并从雷达探测距离和探测概率的角度评价飞机的隐身性能[5]。然而仅从飞机的隐身角度出发,很难全面考虑到飞机的实战情况以及空地对抗中对雷达探测、跟踪性能的影响程度。
美军在考虑隐身飞机的实战化需求后,通过在F-22和F-35战机平台加载电子干扰设备,准备将二者改进为具备先进电子战能力的EF-22和EF-35战机,全面提升隐身战机的作战能力。当前由于客观条件的局限,国内外尚未形成对隐身飞机电子战能力的系统研究和客观评估。文献[6]仅以非隐身战机为研究对象,通过建立飞机敏感性模型,重点研究了非隐身战机的电子战能力。文献[7-9]在对干扰机的随队模式和干扰特点进行分析后,建立了干扰机随队干扰对抗雷达的具体编队方式[10];文献[11-13]对干扰条件下的雷达探测距离进行了详细研究。文献[6-13]是基于非隐身战机所展开的飞机电子战研究,并没有考虑隐身战机的电子战模式。
针对此问题,本文借鉴文献[1-5]中对隐身飞机隐身性能的研究方式,结合文献[6-13]中普通干扰机的电子战情形,建立隐身飞机随队干扰模型,通过解算飞机姿态、获取动态RCS等过程,研究了隐身飞机随队干扰模式下,雷达探测目标机的性能变化。
1 隐身飞机随队干扰模型
1.1 问题描述
考虑图1所示场景:为掩护己方目标机突防作战,装载电子干扰设备的隐身飞机随队飞行掩护。其中,目标机侦测到地面防空雷达的威胁信号后,向隐身飞机交互信息。隐身飞机在确保自身安全的前提下,立即释放干扰,以降低雷达探测性能,确保目标机安全突防作战。其中,Rj是隐身飞机随队干扰的干扰距离;Rmax是地面雷达的最大作用距离;Dj是随队干扰的烧穿距离[14-15]。
上述作战场景的限制因素为:1)目标机与隐身飞机单架组队,雷达无组网形式;2)飞行速度一致,编队位置相对稳定;3)干扰信号主要从雷达主瓣进入;4)干扰样式为噪声压制干扰;5)航迹参数设置考虑烧穿距离限制;6)所处电磁和大气环境理想。
1.2 隐身飞机模块
1.2.1飞机敏感性分析
隐身飞机的RCS是姿态角的敏感函数,是动态变化过程。其中,方位、俯仰和滚转能够反映飞机的即时姿态,确定飞机与雷达的相对视线位置,也可以确定飞机的即时RCS值。因此,通过二维姿态角变化获取飞机的即时RCS值是动态RCS序列生成的常用手段。
1.2.2动态RCS获取步骤
RCS幅度起伏特性是描述目标动态过程的重要应用之一,其获取过程包括航迹参数设置、飞机受力分析、时变姿态解算和电磁仿真计算四个模块,具体流程图2所示。
1.2.3模块设计
(1)编队航迹参数设置
编队飞行航迹具体设置如下:
1)平飞姿态仰角δ=0°,转弯飞行姿态仰角δ<5°; 2)维持飞机转弯的滚转角始终是η=30°;3)编队航迹参数设置具体见表1。

表1 航迹参数设置
依据航迹参数,图3给出了隐身飞机和目标机的飞行航迹及与地面雷达的相对位置关系。
隐身飞机随队航迹图3所示,在整个编队飞行过程中,目标机只有侦测到雷达的发射信号时,隐身飞机才会相应释放干扰,进行干扰掩护。平飞航迹中,目标机尚未进入雷达可探测区域,因此,本文仅考虑转弯航迹的随队干扰情况。
(2)飞机受力分析
图4给出了隐身飞机维持转弯姿态的受力情况。
本文建立了飞机转弯过程的动力学方程组:
(1)
式(1)中,发动机推力T在同一高度的飞行平面上与空气阻力D始终保持平衡。气动升力F的水平分量是转弯飞行的向心力L,垂直分量与重力G相平衡,m是飞机质量,g是一般重力加速度。
(3)时变姿态解算
1)坐标系定义
雷达坐标系(O-XRYRZR):以地面雷达质心为坐标原点O,坐标轴规定如下:XR轴沿O所在的纬度线指东,YR轴沿O所在的经度线指北,XR,YR,ZR满足右手法则。
机体坐标系(O-XTYTZT):以飞机质心为坐标原点O,OXT轴指向机体对称平面的机头方向,OYT轴垂直机体平面向左,XT,YT,ZT满足右手法则,图5所示。
图5中,机体坐标系中的φ,θ,η分别是飞机的方位角、俯仰角和滚转角,具体可由雷达与机体坐标系的转换关系和飞机的具体位置解算。
2)坐标系转换
图6给出了解算视线方位角φ(t)和视线俯仰角θ(t)的解算过程。
雷达坐标系与机体坐标系的转换关系[1-3,16]为:
(2)
式(2)中,坐标(x(t),y(t),z(t))表示雷达坐标系中任意一点的位置;(xT(t),yT(t),zT(t))是点(x(t),y(t),z(t))相应在机体坐标系中的坐标位置;(xR(t),yR(t),zR(t))是飞机所处位置在雷达坐标系中的坐标;T是雷达坐标系到目标坐标系的转换矩阵。根据两个坐标系中方位角、俯仰角和滚转角逆时针旋转变换关系,转换矩阵T可用式(3)表示。
(3)
式(3)中,Tγ、Tθ、Tφ分别是滚转角、俯仰角以及方位角逆时针旋转到目标坐标系中的转换矩阵。将雷达坐标原点(0,0,0)代入式(4),则时变的视线姿态角[17]表示为:
(4)
视线姿态角解算结果如图7所示。
隐身飞机沿转弯航迹飞行共需时间154 s。每一时刻分别对应一组视线方位角和视线俯仰角,以描述飞机的即时姿态。
(4)电磁仿真计算
1)在电磁计算平台FEKO中设置仿真条件(工作频率:5.8 GHz、极化方式:HH),计算某型隐身飞机的全空域静态RCS数据;
2)时变的视线姿态角构成二维数组,在对应静态RCS数据库中提取即时姿态的RCS值;
3)利用Matlab软件编程,按时变姿态角对应的顺序组合即得到动态RCS序列。
图8给出了飞机转弯过程中,在0~154 s内动态RCS的仿真结果。
邻近时间的RCS起伏变化幅度大,没有一定的函数规律可循,起伏随机性较强,说明微小的姿态变化能够导致飞机隐身性能的强弱之别。在0~154 s的时间内,RCS起伏幅度在-35.939~9.203 dBsm范围内。
2 雷达探测性能
雷达探测性能一般由探测距离和探测概率量化评估。理论上分析,随队干扰目的在于采取噪声压制方式,提高干信比,缩减雷达探测距离范围,减小雷达探测概率,从而降低探测性能,掩护目标机突防。因此,评估隐身飞机随队干扰对雷达效能的影响,需从探测距离和探测概率量化研究。
2.1 雷达探测距离
雷达探测距离方程[6]具体描述了探测距离的相关因子及其相关关系。对于某部雷达而言,探测隐身飞机的距离范围具有时间变换性和空间随机性的特点。
1)无干扰状态的雷达探测距离
在设定检测门限,给定虚警概率的前提下,无干扰状态的时变雷达探测距离[18]为
(5)
式(5)中,各参数具体含义如下:Pt表示发射机的峰值功率;Gt=Gr为收发一体天线的主瓣增益;σt为t时刻飞机的RCS值;λ为雷达工作波长;k为波尔兹曼常数;T0为内部噪声温度;Bn为接收机带宽;Fn是接收机的噪声系数;Ls是雷达各部分损耗引入的损失系数;(S/N)min是雷达检测信号所需的最小可检测信噪比。
2)干扰状态的雷达探测距离
随队干扰条件下的时变雷达探测距离[6]为
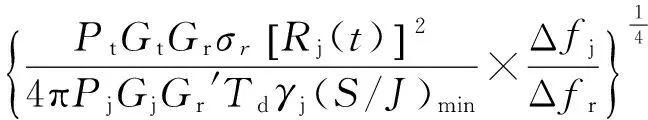
(6)
式(6)中,Pj为干扰设备发射功率;Gj为干扰设备天线增益;Gr′为雷达在干扰方向上的接收天线增益;Rj(t)为t时刻隐身飞机的干扰距离;Δfr为雷达接收带宽;Rd为干扰设备发射机损耗;γj为干扰信号相对雷达天线的极化损失,一般取γj=0.5;Δfj为干扰信号带宽;(S/J)min是最小可检测信杂比。
随队干扰必须充分考虑烧穿距离这一限制因素。烧穿距离是指在干扰条件下,雷达信号质量足够探测跟踪目标时,两者之间的距离。
烧穿距离公式均采用dB形式处理各种物理量。距离以km为单位,频率以MHz为单位,雷达截面积以m2为单位。
对单基地雷达而言,具有收发共用天线。因此,接收机接收到的信号功率[15]为
S=Pt+Gt+Gr-103-20lg(F)-40lg(Dj)+10lg(σ)
(7)
式(7)中,S是接收机输入端的信号功率,dB;F为发射信号频率,MHz。
进入接收机输入端的干扰功率[15]为
J=Pj+gj-32-20lg(F)-20lg(Rj)+Gr′
(8)
式(8)中,J是接收机接收端的干扰功率,dB。
考虑图1设定的隐身飞机随队干扰场景,干扰信号与目标回波信号以相同角度进入天线,此时有:Gr′=Gr,则干信比表示为
J/S=71+Pj-Pt+Gj-Gt-
10lg(σ)-20lg(Rj)+40lg(DJ)
(9)
整理后为:
40lg(Dj)=Pt+Gt+10lg(σ)+
20lg(Rj)-71+J/S-Pj-Gj
(10)
则烧穿距离[15]dj为
dj=10[40lg(Dj)/40]
(11)
对于随队干扰而言,满足dj (12) 上式中,θ0.5为雷达天线主瓣宽度;K是与雷达天线特性有关的常数,一般取K=0.04~0.1;θ为雷达主瓣方向与雷达到干扰机连线方向的夹角。结合式(6)和式(12),隐身飞机某一时刻释放干扰对雷达探测距离的缩减程度图9所示。 图9说明:干扰方向天线增益Gr′是θ的函数,干扰条件下的雷达探测范围是以雷达与干扰机连线为中线,外推延伸的心状曲线。其中,压制后的雷达探测区域称为暴露区;雷达缩减区域是掩护区。且θ=0°方向干扰效果最好,此时干扰机位于雷达主瓣波束内,雷达探测距离最小为Rmin;θ=180°方向干扰效果最差,雷达最大探测距离为Rmax。 所建随队干扰模型中,Gr′=Gr、Rj(t)=Rt,此时θ=0,隐身飞机和目标机始终处于雷达主瓣方向。即随队干扰时,目标机任意时刻的雷达探测距离为最小的Rmin。 1)信噪比-信干比 信噪比(Signal to Noise Ratio, SNR):对式(5)进行变换,可得信噪比计算公式: (13) 信干比(Signal to Interference Ratio, SIR):对式(6)进行变换,可得信干比计算公式: (14) 信(噪声+干扰)比:文献[11]给出了干扰条件下雷达系统中信号与干扰和噪声之和的比值: (15) 2)雷达探测概率 (16) (17) 式(17)中,Q函数积分运算,为简化Pd运算,North提出了近似计算公式(18)。 (18) (19) 3.1.1隐身飞机探测距离 常规体制雷达参数设置见表2。结合表2及隐身飞机转弯的动态RCS序列,图10给出了隐身飞机在0~154 s的转弯过程中,飞机实际空间距离和雷达探测距离的时变情况。 编队转弯过程中,隐身飞机的时变雷达探测距离起伏剧烈,由飞机RCS决定。图10表明,转弯过程中,隐身飞机的即时空间距离远大于雷达探测距离,在距离关系上具备编队飞行掩护目标机的条件。 表2 雷达参数设置 3.1.2目标机探测距离 1)无干扰状态的雷达探测距离 假设目标机的RCS是10 dBsm,依据式(5)可得目标机的雷达探测距离和实际空间距离的即时关系,见图11。 随队的隐身飞机不释放干扰时,0~154 s内目标机的雷达探测距离始终是57.16 km。图11中,0~19.53 s和134.47~154 s时间内,目标机的即时空间距离大于雷达探测距离,即飞机尚未进入雷达探测区域范围;19.54~134.46 s内目标机在雷达探测范围内突防飞行,目标机将可能被地面雷达探测、跟踪到。 2)干扰状态的雷达探测距离 为便于比较分析及描述客观的实战场景,隐身飞机从转弯伊始(0 s)释放干扰,转弯结束(154 s)停止干扰。 隐身飞机随队干扰设备参数设置见表3。 表3 干扰设备参数设置 随队噪声压制干扰需要考虑雷达烧穿距离的限制。图12给出了隐身飞机转弯飞行过程中烧穿距离的时变特点。 雷达烧穿距离的时变范围在1~2 km。显然,dj 依据式(6),得到随队干扰条件下,目标机的实际空间距离与雷达探测距离的时变情况,图13所示。 随队干扰开始后,雷达探测范围基本被压制缩减至40 km以内。且对应干扰状态下每个时刻的雷达探测距离都是最短干扰压制距离Rmin。图13所示,随队干扰的效果是雷达探测距离低于飞机的即时距离,此时雷达将无法正常探测、跟踪目标,目标机突防安全。 设定检测门限(Pfa=10-6),求解分析隐身飞机和目标机在转弯过程中雷达探测概率的时变情况。 3.2.1隐身飞机探测概率 利用转弯过程中的动态RCS序列,结合式(13)及式(18),图14给出了隐身飞机在0~154 s内雷达瞬时探测概率的时变特征。 从图14可以看出,在0~154 s内,雷达可探测到隐身飞机的概率低、时间短、不连续,很难在时空域上形成连续的探测跟踪过程,目标突显时间极短,隐身时域区间长。即隐身飞机满足编队飞行掩护目标机作战的条件。 3.2.2目标机探测概率 比较分析目标机在有无随队干扰状态的探测概率变化,需求解干扰前系统的时变信噪比和干扰后系统的时变信干比数值。 1)信噪比-信干比 信噪比和信干比均是时域函数。根据式(12)和式(13)的计算方法,目标机在转弯飞行时,信噪比和信干比在0~154 s的时变情况图15所示。 图15表明:对于既定体制雷达,转弯航迹中探测10 dBsm的目标机时,当隐身飞机处于随队无干扰状态时,雷达系统信噪比的时变范围在15~30 dB之间;当隐身飞机处于随队干扰状态时,系统信干比的时变范围为-40~-30 dB。 2)雷达探测概率 信噪比反映雷达体制属性,在隐身飞机随队无干扰状态,目标机的雷达瞬时探测概率图16(a)所示;信干比主要表现干扰设备的干扰性能,在隐身飞机随队干扰状态下,结合信噪比和信干比的时变数值,利用式(6),求解目标机的时变信(噪声+干扰)比,然后根据式(19)得到目标机受到干扰掩护时的雷达瞬时探测概率图16(b)。 比较分析图16(a)(b)可知: 1)隐身飞机在转弯航迹中有无进行随队干扰,对目标机的雷达瞬时探测概率影响较大。无干扰状态下,目标机在搜索时间段内能够被雷达探测到,如图16(a)所示,目标机的雷达瞬时探测概率在探测时区内几乎均能达到100%,目标机面临的危险系数提高;干扰状态下,目标机在0~154 s内的雷达瞬时探测概率比无干扰状态降低了6个量级,如图16(b)所示,雷达探测效能基本失效,目标机能够实现安全突防作战的目的。 2)比较图16(a)和(b),隐身飞机随队干扰的前提是编队飞行的目标机面临地面防空系统的威胁时做出的电子对抗行动。与普通干扰机随队干扰不同,隐身飞机以其优越的隐身性能和良好的机动能力,可抵近防空系统随队掩护作战,且能保证自身飞行安全,进而大幅度提高了随队飞行作战的时域和空域范围,在战术上具有突破性。 本文提出了基于隐身飞机随队干扰的雷达探测性能评估模型。该方法建立了编队飞行航迹,设定了目标机的RCS值,通过分析隐身飞机飞行姿态与坐标系转换关系,确定了飞机的动态RCS序列。并依据雷达距离公式和探测概率模型,比较分析了有无随队干扰状态下,目标机的雷达探测距离和探测概率的时变情况,分析结果表明:隐身飞机在随队干扰过程中,在同时满足编队距离以及发现概率的限制条件后,能够缩减雷达的探测距离范围,减小雷达的瞬时探测概率,进而降低雷达的探测性能,提高了目标机的突防生存力,且在实战中为交战双方积累隐身飞机的电子战经验提供了参考。 [1]刘佳,方宁,谢拥军,等.姿态扰动情况下的目标动态RCS分布特性[J].系统工程与电子技术,2015,37(4):775-781. [2]戴崇,徐振海,肖顺平.雷达目标动静态RCS特性差异分析[J].信号处理,2013,29(9):1256-1263. [3]戴崇,徐振海,肖顺平.非合作目标动态RCS仿真方法[J]. 航空学报,2014,35(5):1374-1384. [4]沙文浩,姜秋喜,潘继飞,等.网络雷达对抗系统反隐身有源检测模型[J].探测与控制学报,2017,39(5):102-108. [5]陈世春,黄沛霖,姬金祖.从探测概率的角度评价飞机的隐身性能[J]. 航空学报,2015,36(4):1150-1161. [6]宋海方,肖明清,吴华,等.不同机载电子干扰条件下的飞机敏感性模型[J].航空学报,2015,36(11):3630-3639. [7]陈晓榕,李彦志,刘呈祥,等.随队支援干扰飞机发展历程及作战运用[J].四川兵工学报,2013,34(11):62-65. [8]李文鹏,杨文,廖明飞,等.低速平台随队干扰编队设计及过程分析[J].火力与指挥控制,2015,40(5):175-183. [9]倪天权,王建东,刘以安.随队式干扰对抗组网雷达的目标航路规划研究[J].兵工学报,2010,31(12):1599-1603. [10]梁海朝,王剑颖,孙兆伟,等.多小型飞行器自主编队姿态协同控制方法[J].哈尔滨工业大学学报,2016,48(4):13-19. [11]Shen T Y, Ding JJ, Ding Y, et al. A method of detection performance modeling in jamming condition based on radar network system [C]//Proceedings of 2011 IEEE CIE International Conference on Radar, Chengdu: IEEE, 2011:1366-1369. [12]罗金亮,王雷,王平平,等.航空随队支援干扰掩护区仿真建模研究[J].火力与指挥控制,2016,41(6):173-176. [13]Lv M J, Zhou M, Du Q L. The integrative application of anti-jamming technology for radar[C]//International Workshop on Intelligent Systems & Applications, Wuhan: IEEE, 2010:1-4. [14]修继信,李东海.影响雷达烧穿距离的要素分析[J]. 舰船电子对抗,2008,31(4):51-54. [15]Adamy D.EW101:电子战基础[M].王燕,朱松,译.北京:电子工业出版社,2013:118-124. [16]石章松,刘忠,王航宇,等.目标跟踪与数据融合理论及方法[M].北京:国防工业出版社,2010. [17]袁修久,赵学军,李嘉林.基于航迹的飞机姿态角建模与仿真[J].系统工程与电子技术,2016,38(4):889-894. [18]敖齐,方斌,黄晨.基于实时RCS的雷达探测概率模型[J]. 计算机仿真,2016,33(7):1-5.2.2 雷达探测概率
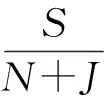
3 仿真分析
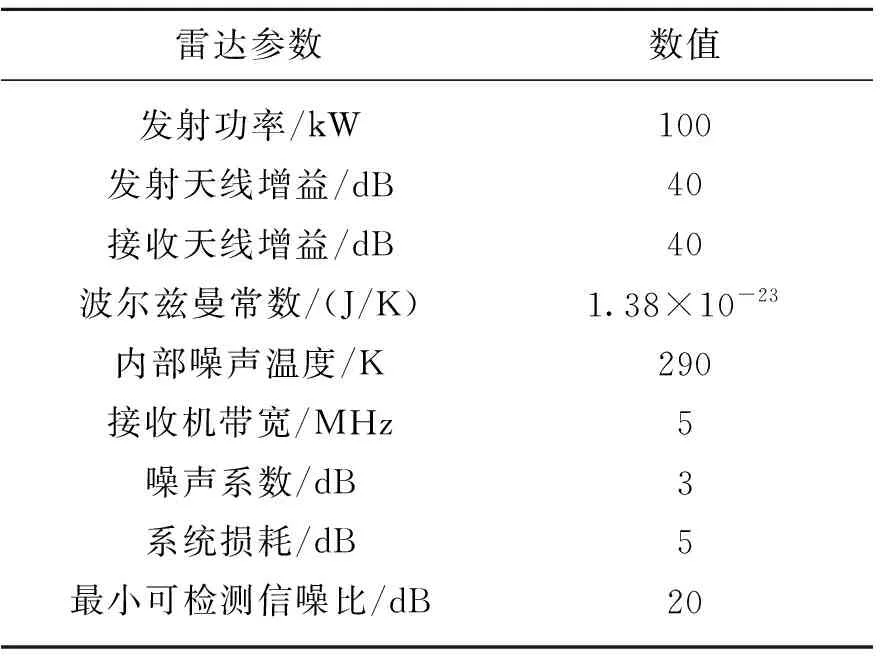
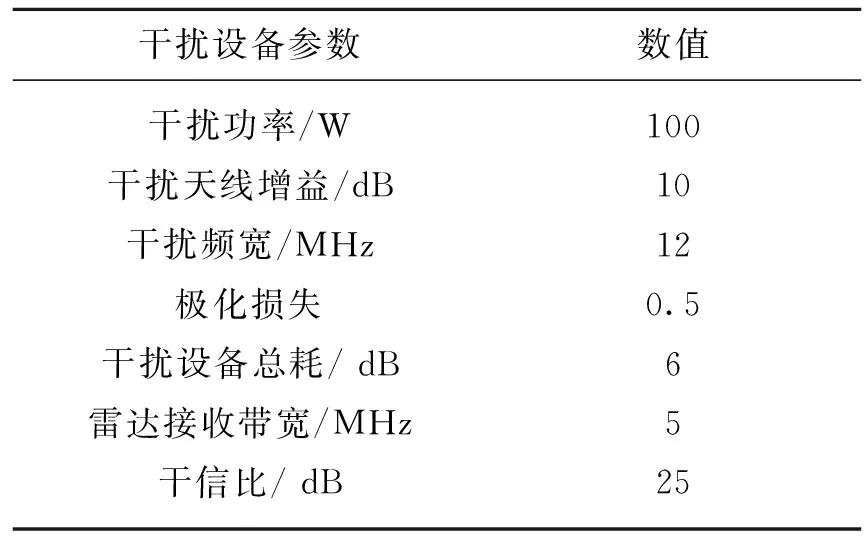
3.1 探测距离
3.2 探测概率
4 结论

