实施学情前测 优化教学过程——以“平行四边形的面积”的教学为例

江苏苏州吴江区程开甲小学 时 坤

学情前测是指教师在开展教学活动之前，在理解和钻研教材的基础上，采用试题检测、调查问卷、学生访谈、操作探究等多种形式，对学生已有的知识基础、学习技能、生活经验、兴趣爱好等进行测试，分析学生在本节课中的学习起点以及存在的困惑，将分析所得的学情与参考目标进行比照，科学合理地安排教学活动，最终让整个教学更具有前瞻性、准确性、层次性和有效性。

一、解读教材，确定可测项目

有效的教学基于教者对教学内容的全面把握，教师能正确地解读教材，理解编者的编排意图，确定教学重难点，乃是教学的根基。因此，笔者在教学之前基于对教材的分析，确定了以下几个前测项目：

（1）“平行四边形的面积”安排在五年级，低年级教材中安排了初步认识平行四边形，学生能从直观上判断一个图形是否是平行四边形。中年级时，学生也掌握了平行四边形的特征以及它的高等相关内容。平行四边形的底和高在本课的教学中有着非常重要的作用，为了了解学生是否明确平行四边形底与高的对应关系，能否熟练地画出相应的高，笔者在前测中设计了第一个问题：你能画出下面两个平行四边形指定底边上的高吗？

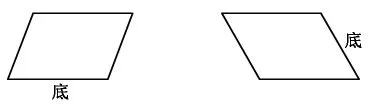
（2）中年级的教材还编写了认识周长、求长方形和正方形的周长、认识面积、求长方形和正方形的面积等内容，学生在之前也掌握了运用数方格、转化的方法求图形周长和面积的经验。这些学习经验为本节课的学习打下了重要基础。但是，也有学生会受到长方形面积计算公式的负迁移影响，误认为求平行四边形的面积就是将两条邻边相乘。为了了解学生真实的学习起点以及他们的创造性思维，笔者在前测中设计了第二个问题：你能求出下面这个平行四边形的面积吗？简要说明你的解题思路。（可以画图，也可以用语言描述）

二、实施前测，把握教学起点

笔者通过课前试题检测和学生访谈的形式，对本校五（7）班49名学生进行学情前测，试图了解他们真正的想法，从而找准学生的学习起点，实施有效的课堂教学。笔者通过前测发现：

在第一个问题中，全班49人中有44名学生较明确平行四边形底与高的对应关系，能熟练地画出相应的高。所以笔者认为，在教学平行四边形的面积计算时，不需要指导学生复习底与高的相关知识，这样可以为后面操作探究提供充足的时间。

在第二个问题中，笔者发现有以下几种情况：

（1）全班有32名学生列式7×4。 其中，有19名学生是将平行四边形沿高剪成一个三角形和一个直角梯形，然后通过移一移、拼一拼的方法转化成长方形，进而求出面积。有3名学生是将平行四边形沿高剪成2个直角梯形，然后转化成长方形计算出面积。还有10名学生并没有说明理由，通过访谈了解他们中有一部分学生看过并记住了平行四边形面积的计算公式，一部分学生不知道如何阐述理由。

（2）有11名学生用邻边相乘,即7×5。

（3）有4名学生列式（7+5）×2，将面积概念与周长概念混淆。

（4）有2名学生列出了没有意义的算式。

从前测的结果看，邻边相乘这种解法在学生首次接触平行四边形面积计算时必然会出现，于是笔者就这种典型问题对学生进行了访谈，试图了解他们问题背后的想法。

生1：我把平行四边形变成长方形，每边的长度相同，这样图形的面积就不会改变，就可以用求长方形面积的方法来求平行四边形的面积了。

生2：因为平行四边形是一种特殊的长方形，所以我觉得应该也用“长×宽”。

生3：通过画图，先画出一个长方形，将长方形的左上角向右推，接着画出平行四边形（如下图），指出：变成平行四边形后，斜着的边不知道长度，但平行四边形的高就是宽，所以可以邻边相乘。

很明显，部分同学由于学习了长方形、正方形面积以及平行四边形的“不稳定性”特征，认为平行四边形可以通过拉动变形成为长方形，所以可以用“长”ד宽”来计算。同时表明大多数学生已有一定图形转化的意识，但是学生心中的转化只是表面形状的变化，并没有真正理解等积变形的转化思想，而这是本节课学习的关键，也是作为后面其他平面图形的面积计算的推导依据。因此在教学时，要直面学生的疑惑，帮助学生理解“为什么要转化、怎样转化”。

三、教在起点，优化教学活动

只有教师正确把握学生学习的出发点并加以利用，才能引导学生进行有效的数学学习，才能做到有备而来，满载而归。

（一）基于前测信息，引入探究

笔者在课前根据前测信息对学生进行分组，把不同层次的学生组合在一起。课上，笔者出示之前通过前测得到的求平行四边形面积的几种主要方法：①7×4=28（平方厘米）；②7×5=35（平方厘米）；③（7+5）×2=24（平方厘米），引导学生判断哪种是求平行四边形面积的正确方法。

生1：（7+5）×2=35（平方厘米），这个算式求的是周长，而不是它的面积。

生2：因为平行四边形是一种特殊的长方形，所以7×5=35（平方厘米）是正确的。

生3：因为将平行四边形沿高剪成一个直角三角形和一个梯形，然后把直角三角形平移到另一边，就能变成一个长方形，所以7×4=28（平方厘米）是正确的。

……

通过这个环节的设计，让学生的困惑一开始就暴露出来，利于帮助学生带着问题进入下一个环节，从而使教学更具有针对性，也变得更有效。

（二）提供学习素材，探究本质

要让学生真正理解转化的本质，首先得修正他们原有的认知错误，于是笔者为每名学生提供长方形框架，引导学生观察在不同倾斜角度下其面积的变化情况，让学生感知“长×宽”的不合理性。接着，通过三个问题的设置，给学生留下充足的操作和交流的时间，引导学生结合手中的学具，自主探索出求平行四边形面积的正确方法，理解转化的本质。

（1）不管是用“剪、拼、移”的方法，还是用拉伸的方法，都是把平行四边形变成了长方形，那他们有什么不同呢？

生：用“剪、拼、移”的方法，得到的长方形面积和原来平行四边形的面积是一样的，而用拉伸的方法所得面积是不一样的。

（2）怎样转化才能使平行四边形的面积不变？

生：只要沿着平行四边形的高剪，那么它的面积就不会发生改变，反过来，高变化了，面积也变了。

（3）把平行四边形剪拼成长方形后，这两个图形之间有什么关系呢？

生：因为平行四边形的高跟长方形的宽是一样，平行四边形的底跟长方形的长也是一样的。长方形的面积公式是“长×宽”，所以平行四边形的面积公式是“底×高”。

（三）经历数学归纳，理解内化

对于新知需要及时组织学生巩固运用，才能起到理解内化的效果。笔者在学情前测中发现本班学生具有很强的好奇心和探索精神，于是结合学生的情感态度，设计习题：是不是所有平行四边形的面积都可以转化成长方形来计算呢？在方格纸上自己画一个任意形状的平行四边形，并验证自己的想法。

通过这道题目的练习，不仅使得研究素材更加丰富，研究活动更具科学性，同时也为学生提供变式，进一步帮助学生归纳总结出平行四边形的面积计算公式，让学生感受学习数学的成就感。

四、教学效果及反思

教学完成之后笔者随即对学生的掌握情况进行了反馈考查，设计如下：

（1）判断：图中哪个平行四边形的面积可以用5×3表示？

（2）你认为下图中两个平行四边形的面积相等吗？为什么？

反馈结果：第一题49人全部答对，正确率为100%；第二题45人答对，正确率为92%。

当堂反馈表明，教学中的难点问题得到有效突破，绝大多数学生能够掌握平行四边形的面积计算公式。新课标一直倡导以学生为主体，真正地将课堂还给学生，而学情前测就是进行高效课堂教学的有力抓手，可以帮助教师真实地了解学生的学习起点、学习需求和学习困惑，进而设计层次分明的教学活动，帮助不同层次的学生在数学学习上得到不同的发展。♪