陪学生做研究
张丽丽
1978年,斯坦福大学心理学教授 Carol Dweck做了一项实验,找来一群孩子玩拼图,观察他们的行为和情绪反应。实验之前,教授就预料到,孩子面对困难时会有不同的反应,事实也确实如此。伴随拼图越来越难,有些孩子开始抗议:“现在一点都不好玩了!”后来实在受不了,坚持要“放弃”,甚至直接将拼图推到地上。但她没预料到的是那些“成功孩子”的表现,当面对特别难的拼图时,一个10岁的男孩拉来一张椅子坐下,搓着双手,大喊一声:“我喜欢这个挑战!”另一个小男孩露出喜悦的表情,斩钉截铁地说:“你知道吗?我期待这个拼图会非常有意思。”
Carol Dweck教授的这项实验引发了笔者对数学教学的思考。这样的情形在我们的数学课堂中何尝不是司空见惯呢?为什么两类学生在面对困难时会有如此大的区别?Carol Dweck教授发现,这些学生之间的差异在于思维模式,她提出,人的思维模式有固定型和成长型两种思维模式。而教师要做的就是通过教学活动和行为,助推不同水平的学生养成成长型思维模式。
小学高年段学生已经具备了一定的认知基础,因此,笔者从三年级开始就以“周作业”的形式,开展学生感兴趣、贴近生活又跟教学内容息息相关的系列综合实践活动,以培养学生养成成长型思维模式。
一、活动主题的确定
数学综合实践活动要凸显出一定的研究性、项目化色彩,在活动中激发学生的探究热情和能力,逐渐形成成长型思维模式,以便为中学的研究性学习、课题学习等奠定良好的基础。
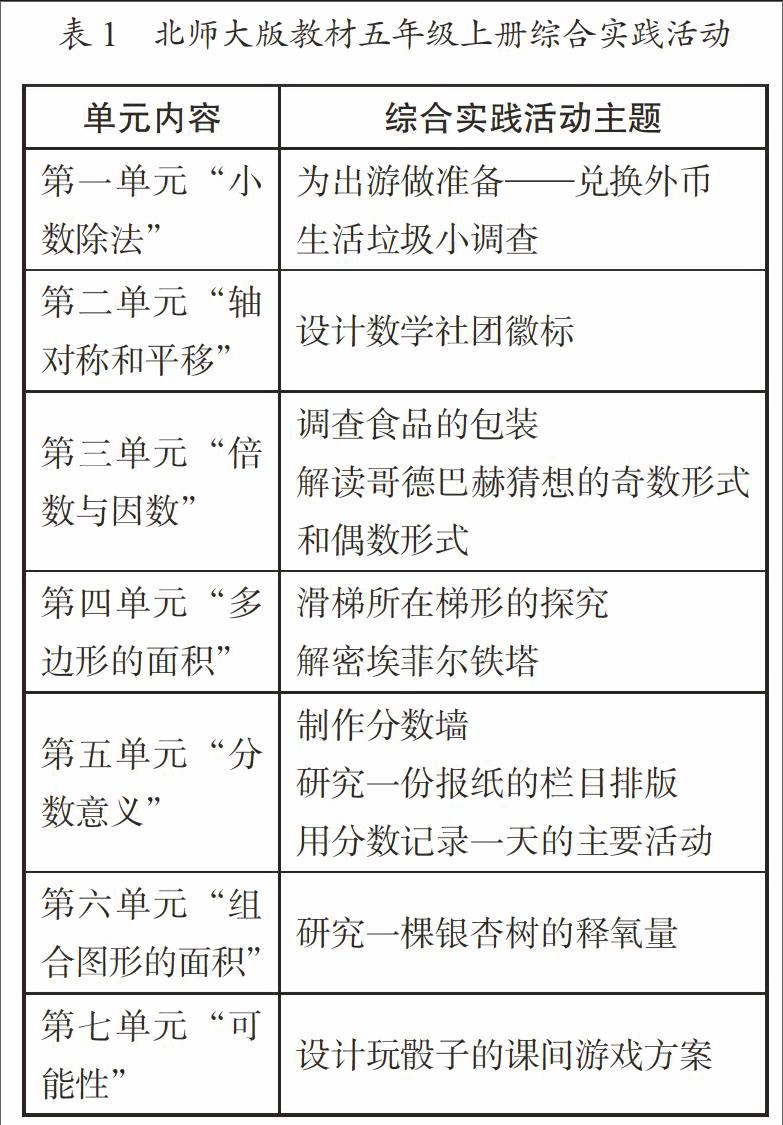
以北师大版教材五年级上册综合实践活动为例(见表1),笔者在教学中,让数学综合实践活动主题拥有一种结构,这种结构具有一定的开放性,结构中的各个部分都是彼此关联的,以便在活动实施过程中,让学生能够在这种“骨架”中,进行有目标、有条理的活动
二、综合实践活动主题来源
荷兰的数学教育以“现实数学教育”(Realistic Mathematics Education)思想而闻名世界。现实数学教育思想的提出受荷兰著名数学家弗赖登塔尔的数学观影响,强调数学必须联系现实,贴近学生的经验和社会生活。因此,每学期的数学综合实践活动主题主要来源于以下几个方面。
第一,现实生活。如笔者将北师大版四年级下册一单元“小数的意义和加减法”的综合实践活动主题确定为“探秘共享单车”,旨在探究如何在数学的角度分析、解读。与学生聊过之后,他们纷纷说出了自己感兴趣的切入点,这一主题活动就确定下来。
第二,教学难点。如笔者将北师大版四年级下册三单元“小数乘法”的综合实践活动主题确定为“生活中的分段计价问题”;将北师大版五年级上册一单元“小数除法”的实践活动主题确定为“为出游做准备—兑换外币”。就以往的教学经验,一部分学生理解分段计价和汇率问题十分困难,难在问题产生过程中数据多,数量关系复杂,所以设计这样的实践活动,一方面是让学生面对这样的问题首先不陌生;另一方面是让学生以主人公身份,从问题产生的第一个环节开始到最后的问题解决,经历“从头至尾”的全過程。对于思维能力弱的学生来说,每一个数据的产生都有其现实意义,不会“厘不清”数量关系。
第三,学习困惑。如笔者将北师大版四年级下册二单元“三角形和四边形”的实践活动主题确定为“力大无比的牙签桥”,学生在肯定三角形稳定性的同时,提出“三角形这一特性到底有多么‘稳固”。最终,当学生通过自己的双手成功搭建的牙签桥,并且站上一个50千克重的自己时,他们感慨三角形原来可以这样力大无穷。再如,笔者将北师大版五年级下册三单元“倍数与因数”的实践活动主题确定为“解读哥德巴赫猜想的奇数和偶数形式”。学生对神秘“质数”产生了非常浓厚的兴趣,提出“难道质数就真的没有规律可言”的质疑,在无数次的猜想、验证、批判、再猜想、再验证的过程中,学生提出,质数都分布在6的倍数左右,有了这样的猜想后,感兴趣的学生进行了更深层次的探索:因为6是2和3的倍数,一个数如果除以6余数会是1、2、3、4、5,当余数是2和4的时候这个数都能被2整除,当余数是3的时候都能被3整除,当余数是1或5的时候很有能就是质数了,余数是1或5时,不就是6的倍数的左右。
学生在这样的综合实践活动中,互相启发,大胆设想,“探秘”数学世界之大,创造了一个又一个的奇迹。
三、综合实践活动的评价
为了鼓励学生,笔者跟他们说:“我未来的数学家们,对于你们的伟大探秘之旅,张老师有物质和精神的鼓励。”
“物质”奖励是指纳入我校综合评价体系的期末成绩中的“能力”这一项的单项评价。根据学生互评和师评,形成能力水平的评价成绩。“精神”奖励是指书,笔者每个学期都会给学生精选适合其年龄段的数学读物,如作为奖励,笔者在五年级下学期订购了《数学阅读》,供学生
借阅。
通过综合实践活动,不同能力水平的学生都会在感兴趣的实践活动中,不断地整装思维模式,探秘数学世界之大。这样的教学行为从孩子三年级开始,历经小学3年,在循序渐进、螺旋式上升的过程中实践着,而笔者也计划在六年级的教学中,将“主题设计”的自主权交给学生,这种自主是在教师“诊学、导学、助学”基础上的自主,从而使学生在活动中形成系统化、结构化的数学思考,发展逻辑思维,培养应用意识和实践能力,经历提出、理解、探索和解决问题的过程,获得全面的活动体验,形成成长型思维模式。
责任编辑:李莎
lis@zgjszz.cnendprint

