引领深度对话 助推思维生长

江苏常熟市星城小学（215505） 顾剑珏

语言是思维的工具，思维是语言的内核。深度对话所追求的是思维的对话，它能帮助学生在对话的过程中积极思考，逐渐逼近数学知识的核心，提升学生的思维品质。在实际教学过程中，由于学生的年龄较小，自我思维体系还不完善，这就需要教师讲究组织对话的策略，智慧引领对话过程，助推学生思维拔节生长。

一、捕捉提炼，聚焦思维热点

对话主题一般以问题的形式呈现。问题是诱发学生主动探索新知的源头，是开展深度对话的有效载体。课堂上随机生成的一些问题最能真实反映学生的思维热点，然而，这些问题往往是多样而又不完整的，思维水平也是有差异的，这就需要教师有高度的敏感性，能及时捕捉学生有价值的想法并迅速聚焦重组，从而挖掘对话的深度。

【案例1】“商不变规律”

当学生填表（如图1），讨论并初步感受到商不变规律时，角落里冒出一个声音：“如果是加上或减去同一个数呢？”教师及时捕捉放大，引导学生通过举例，发现除了加（或减）0商不变，其余都会变。

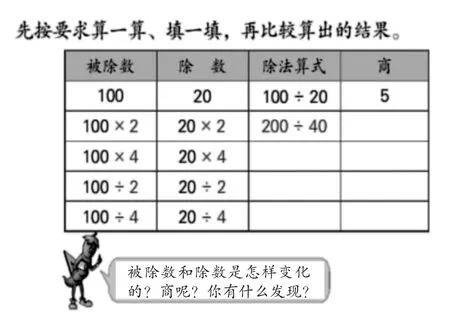
图1

师：只有在加（或减）0这两种特殊情况下商不变，这能不能称为规律？

生（齐）：不能。

师：从表格中我们得出“被除数和除数同时乘或除以同一个数，商不变”，这能不能称为规律？

生1：我觉得也不能，说不定这几个例子也是特殊情况，还需要举更多其他的例子。

（学生举例验证，其中出现了同时乘或除以的数为0的情况）

师：现在你又有什么新的想法？

生2：同时乘或除以的数中，要把0排除掉。

让学生经历合情推理过程，进而发现商不变规律是本课的重要目标。但在以往的教学中，我总觉得验证过程没能贴近学生的实际需要，往往流于形式。此次再教时，恰巧遭遇“意外之音”——“如果是加上或减去同一个数呢？”正是这样一次捕捉放大，使“举例验证”的思想应运而生，触及学生真思维的探究，让学生充分经历研究数学、发现规律的过程，对合情推理也有了更立体、更丰满的体验，思维的严谨性得到了有效提升。

二、掌舵领航，把握思维方向

学生受思维水平限制，课堂对话常常出现方向不明、条理性差的情况，对问题的思考也仅停留在表层。在有些课堂中，出现了“学生想说什么就说什么”“说什么都有道理”的极端现象。对话需要学生大胆地表达，但这不等于就放任学生，在对话的过程中，教师要“掌好舵”，一旦发现学生偏离“航线”，必须及时纠正。

【案例2】“平均数”

师：为了解家里的用水量是偏高还是偏低，我调查了我们小区6户三口之家一个月的用水量。（出示图2）

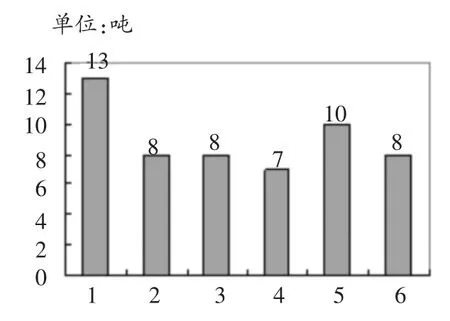
图2

师：每家的用水量都不一样，应该跟谁比呢？

生1：跟7吨比，比7吨少，就说明用水量偏低；比7吨多，就是用水量中等。

生2：8吨才是用水量中等。

生3：如果比13吨多，就说明用水量偏高。

这是某次教学“平均数”公开课中的导入部分，教师意图通过引导学生思考“应该跟谁比”来引出平均数，让学生感受到用平均数作为统计量可以较好地代表一组数据的整体水平。但实际教学结果并不像预期那样，由于三年级的学生缺乏对“平均数”的经验，而教师也没能及时介入引领，致使讨论变得毫无方向。恰恰相反，在案例1中，教师通过对“只有在加（或减）0这两种特殊情况下商不变，这能不能称为规律”“被除数和除数同时乘或除以同一个数，商不变，这能不能称为规律”两个节点处反复叩问，帮助学生适时疏通思维流程，使之朝着正确的方向层层递进。

三、倾听思辨，还原思维困惑

倾听和思辨是一对紧密相连的学习行为，教师组织学生交流自己的想法和观点，能充分暴露学生最原始的思维形态，让课堂对话更具实效，思维也在辨析困惑中走向深刻。

【案例3】“除数是整十数的除法”

教师出示练习：试一试，96÷20=？待学生计算后，教师呈现某学生的典型错误（如图3），全班学生讨论。

生1：16除以20不够商8。

（师顺势呈现第二种典型错误，如图4）

生2：还是不对，4应该写在个位上。

生3：4应该写在十位上，因为是用十位上的9除以十位上的2得来的。

生4：96里面只有4个20，如果把4写在十位上，就变成40个20了。

师：究竟是用96除以20，还是用9除以2？

生5：应该是96除以20，只是在计算时，可以想成9个十除以2个十。

生6：应该把20看成一个整体。9除以20不够除，与6合起来变成96去除以20，已经除到个位了，所以4应该写在个位上。

除数是两位数的除法与除数是一位数的除法在试商时有所不同，本质区别在于需要将除数（20）作为整体来试商，这与学生原有的计算方式不完全相符，从而导致部分学生产生困惑。案例中，教师引导学生围绕错例展开对话，真实暴露学生的错误根源，引发认知冲突，学生通过倾听与思辨逐渐走出计算误区，理解算理，建立起新旧知识稳固的链接，增强了学生质疑探疑的能力。

图3

图4

四、及时点拨，跨越思维障碍

在对话过程中，学生难免出现思维受阻或思维卡壳的情况，这时，就需要教师及时点拨，排除阻断思维的“拦路虎”。通过点拨及时调控教学进程，能积极地发挥教师的组织引导作用，帮助学生突破原有的思维束缚，获得新的发展。

【案例4】“解决问题的策略”

图5

师：（出示图5）你能从表中获得哪些信息？

生1：9:00与7:00比，水位下降12厘米；11:00与7:00比，水位下降24厘米……

生2：水位下降的高度都是“与7:00比”的。

师：怎样理解“与7:00比”的意思呢？请结合观测的时间观察这些下降的高度，你有什么发现？

生3：都是每隔2小时记录一次。

生4：每2小时水位下降12厘米。

从学生的角度来说，仅根据图5提供的数据就发现“每2小时水位下降12厘米”这一规律有一定困难。学生在解读表格信息时，往往只关注了数据纵向的对应，同时又过多强化了表头“与7:00比”这一信息，反而无法触及现象的本质和规律。眼看思维即将“搁浅”，此时，教师及时点拨将学生的目光巧妙引向了数据的横向比较，使学生顺利跨越了思维障碍。

五、有效追问，挖掘思维深度

课堂上，教师在学生思考粗浅处追问，就可以让一部分学生的智慧去启发其他的学生，实现师生、生生之间的思维互动。成功的追问可以巧妙地将问题引向纵深，让学生渐进式地提升认知能力和思维水平。

【案例5】“商不变规律”

师：（出示图6）通过练习，你有什么发现？

先算一算、填一填，再比较算出的结果。

图6

生1：它们的商相同而余数不同。

师：余数的变化有什么规律？结合计算想一想。

生2：被除数和除数同时划掉0，虽然商不变，但余数还是要把划掉的0补上，划了几个0，就要补几个0。

生3：当被除数和除数都乘2时，余数也要乘2。

生4：余数是跟着被除数和除数一起变化的。

通过比较计算结果，学生能感受到余数的变化存在着一定的规律，教师的及时追问将这样的体验进一步放大。随着对话的推进，学生将余数的变化同计算中“划0”的过程联系起来思考，发现被除数和除数同时除以10，余数也跟着除以了10，得出的余数就要乘10，再联系200÷30和 400÷60，发现被除数和除数同时乘 2，余数也要乘2，进而完善了对余数变化的认识。追问让教学由教师“简单的告知”变为学生“深入的发现”，由教师“单向地控制”变为学生“自由地思考”。