带有双滞量的捕食系统的分支分析
李 霞
(河北地质大学<数理学院> 河北 石家庄 050011)
1 引言
由于产期,捕食时间以及食物供给被取代等因素的影响。Volterra[1]等人首先将滞量加入捕食-食饵系统中,这使得新的系统较之原系统呈现出更加复杂的动力学现象,因为当加入滞量后,平衡点将失稳,甚至会使种群密度发生振动的现象,参见文献[2]。
Wu[3]研究了偏泛函微分方程,得到了系统的结论及其可信服的应用实例。Lin[4]等人得到了偏泛函微分方程中心流形的存在性定理。值得注意的是,Faria[5]将她的规范型方法引入偏泛函微分系统中,为研究其Hopf分支及分支方向,分支周期解的稳定性,振幅及其在中心流形上投影的计算公式提供了可靠工具。
在以上文献的基础上,本文着重考虑了具有时滞的捕食系统(1.1),而系统(1.1)乃是熟知的Conway-Smoller常微分系统:

加入时滞之后,将变化为:

在本文中,重点研究(1.2)的稳定性及Hopf分支的存在性。
2 稳定性与分支分析
设条件


那么(2.1)在平衡点附近的线性化部分为:



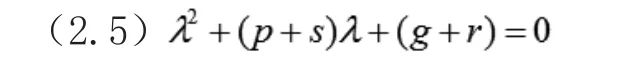
由[6]中给出的关于(2.3)根的分布与横截性条件的结果,可以得到
定理2.1假设 分别为:

那么
既有文献已对(2.1)作了系统研究,当

3 讨论
具有时滞的空间扩散的种群模型遍及至各个邻域。本文仅考虑了捕食系统中的时滞效应,即带有双滞量的泛函与偏泛函微分方程组的稳定性与分支分析。首先给出滞量对强Allee效应常微分系统的影响,通过分析正平衡点的局部稳定性,得到了当滞量穿过一些临界值时系统在经历了Hopf 分支,而进一步分析Hopf分支的方向和分支周期解的稳定性,这将是我们下一步要做的研究工作。
[1] Volterra V.Lecons sur la tlie orie mathematique de la lucte pour la vie [M]. Paris. Gauthiers Villars,1931.
[2] Dai.L.s.Noncontant periodic solutions in predatorprey systems with continuous time delay[J].Math.Biosci,1981,53:149-157.
[3] Wu. J.H.Symmetric functional differential eguations and nural networks with memory Trans.Amer.Math.Soc.1998,350:4799-4838.
[4] Lin.X.So.J W H,Wu.J. H.Center manifolds for partial differential eguations with delays,proc[J].Roy.Soc. Edin.A.1992,122:237-254.
[5] Faria T.Normal Forms and Hopf bifurcations for patial differential eguations with delays[J].Trans.Amer.Math.Soc. 2000,352:2217-2238.
[6] Wei JJ,Ruan S.Stability and bifurcation in a neural network model with two delays[J] Phy,D,1999,130:225-272.

