立体坡面农业四足移动平台姿态控制策略与试验
苏文海,李 冰,袁立鹏,张 辉,谭贺文,息晓琳
立体坡面农业四足移动平台姿态控制策略与试验
苏文海1,李 冰1,袁立鹏2,张 辉2,谭贺文1,息晓琳1
(1. 东北农业大学工程学院,哈尔滨 150030; 2. 哈尔滨工业大学机电学院,哈尔滨 150001)
针对农业四足移动平台在田间行走时的姿态稳定性、负载平稳性差等问题,提出一种立体坡面姿态控制向量策略,在建立四足移动平台运动学模型基础上,通过对一维俯仰、二维横滚坡面姿态姿态向量变化分析,得出立体坡面机身运动姿态角与各腿关节转角的变换方程,而后运用欧拉动力学方程、SLIP理论及次优支撑三角形内稳定裕度理论对四足移动平台平面Trot与坡面Walk步态进行规划。根据Matlab/SimMechanics的坡面姿态仿真试验,对所提出的控制策略进行研究,选择俯仰、横滚姿态变化的限定最小角度;Matlab-Adams虚拟样机仿真试验,验证立体坡面姿态变换方程及其步态规划的可行性,得到四足移动平台在俯仰、横滚均为10°的立体坡面行走时,其俯仰与横滚角变化范围在-2°~2°。通过四足移动平台物理样机进行机身姿态角与关节转角变化关系测试和立体坡面姿态行走试验,试验结果与仿真基本一致,验证立体坡面姿态变换方程及其步态规划的合理性;实现了四足移动平台坡面运动姿态保持水平的目的,提高了立体坡面行走的稳定性;负载平稳性能试验结果表明:该文提出的坡面姿态控制策略,在上、下坡及立体坡面行走时,其负载平稳性与无姿态控制器相比分别提高了15.8%,16.2%和16.0%,增强四足移动平台作为农业移动辅助平台的作业性能,为现代农业移动平台运动姿态控制的设计提供了参考。
农业机械;控制;算法;四足移动平台;姿态角;关节转角;坡面姿态;步态规划
0 引 言
随着现代农业自动化技术的不断提高,农业机器人已成为新的农业机械发展趋势[1-2]。足式机器人作为农业机械的辅助移动平台与其他移动平台相比具有独特的优势,并在农业领域的各个作业场合中得到了广泛的应用[3-6]。
四足机器人具有四足哺乳动物的运动优点,对复杂的地形有着很强的适应性、灵活性,因而逐渐成为众多学者研究的热点[7-10]。四足机器人作为农业机械的辅助移动平台,在坡面行走时,其运动姿态的平稳性直接影响着工作性能。针对运动姿态的平稳性,Sehoon等[11]提出了一种垂直腰关节步行机器人步态分析方法,提高了四足移动平台在坡面行走时的姿态平稳性。冯华山等[12]通过足端轨迹规划和姿态反馈角度对机器人中位各参数进行连续调节来实现坡面稳定行走姿态。韩宝玲等[13]以机器人质心在斜面上的落点到支撑线的距离为判据进行四足机器人坡面运动稳定性分析。孟健等[14]基于NESM判据计算内外倾的稳定裕度并根据其比值进行质心位置调整,实现了四足机器人在坡面地形稳定行走。
综上所述,研究学者以步态规划、姿态反馈和机身质心投影的稳定欲度分析,保证四足机器人在不平路面及坡面行走时的姿态平稳性。但是关于四足机器人在立体坡面行走时保持机身姿态水平,提高其负载平稳性的研究鲜有报道。故而针对立体坡面行走且具有一定负载性能的农业辅助足式移动平台,本文结合四足机器人运动学原理,建立了四足移动平台运动学模型,并对立体坡面姿态控制向量理论进行分析,得到了立体坡面姿态角与腿部关节转角的变换方程,同时规划其行走步态,运用Matlab/SimMechanics、Matlab-Adams仿真及物理样机试验分析验证四足移动平台在坡面行走时的性能。
1 移动平台结构与运动学分析
四足移动平台的结构特点类似于四足机器人,所以在四足移动平台的结构设计上可采用四足机器人的设计方法。同时,根据四足移动平台的结构、拓扑方式及各个关节的相关参数,利用有关连杆坐标运算方法,建立腿部连杆的齐次坐标变换关系并完成运动学的建模。通过四足移动平台各连杆之间的变换关系,得到其运动学的正解和逆解,进而实现四足移动平台足端位置与腿部关节转角的运动学解算。
1.1 结构设计
如图1所示,四足移动平台的结构主要由机身、机节、大腿和小腿组成。四条腿的安装方式采用前肘后膝式的拓扑方式,保证了四足移动平台在行走时的平稳性[15-17]。每条腿包含一个侧摆关节和两个俯仰关节,共由12个伺服电机驱动。其中4个双轴伺服电机安装在侧摆关节负责侧摆驱动,8个单轴伺服电机分别安装在大、小腿关节负责完成其平台在行走时的抬腿高度和前进距离,可实现全方位运动。
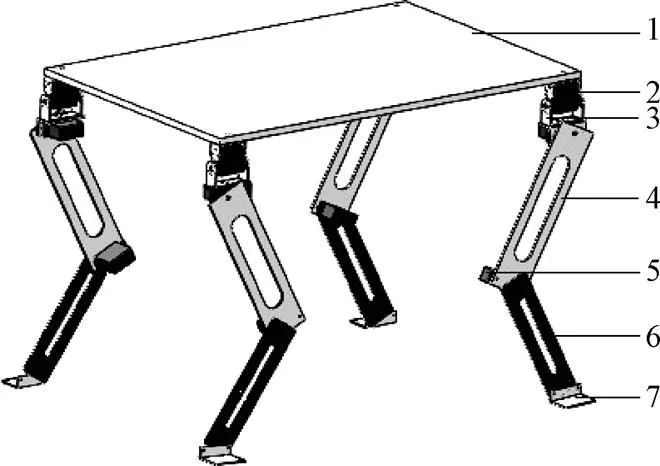
1. 机身 2.双轴伺服电机 3.侧摆关节 4.大腿 5.单轴伺服电机 6.小腿 7.脚板
1.2 运动学方程的建立
建立四足移动平台的运动学模型是求解该移动平台空间运动姿态常用的分析方法。因此,采用D-H法、齐次变换矩阵来描述相邻连杆之间的位姿关系[18-20]。以左前腿为例,建立如图2所示的连杆坐标系。
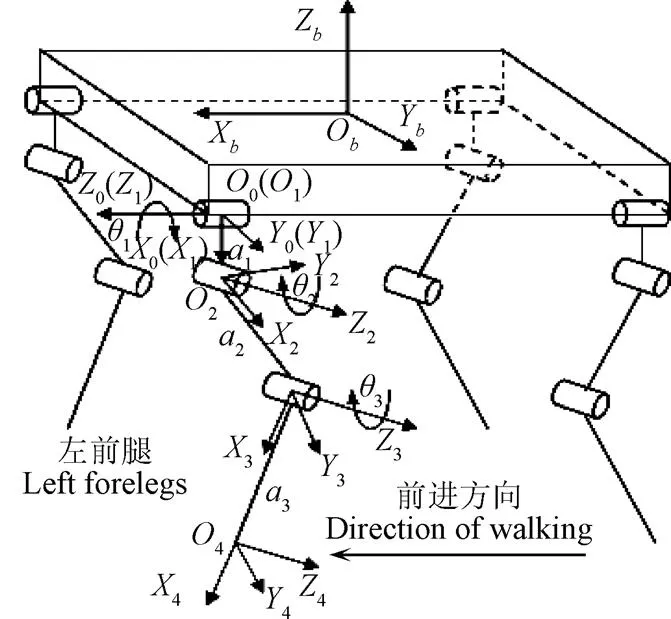
注: ObXbYbZb为机身坐标系;O0X0Y0Z0为基坐标系;O1X1Y1Z1为侧摆关节坐标系;O2X2Y2Z2、O3X3Y3Z3、O4X4Y4Z4分别为大腿关节、小腿关节与足端坐标系;a1为侧摆连杆长度,mm;a2为大腿连杆长度,mm;a3为小腿连杆长度,mm;θ1、θ2、θ3为侧摆、大腿、小腿的关节转角,(°)。
基坐标系建立在侧摆关节上,连杆a坐标系建立在连杆a1的末端上,各连杆坐标Z轴沿着关节轴线方向,X轴沿着连杆方向,其中= 1~4,且足端坐标与小腿坐标方向一致,各连杆变换参数如表1所示。
根据图2建立的运动学坐标及表1定义的参数,采用Paul[21]变换法可以得到
04=01122334(1)
式中01为连杆1相对于基座标的变换矩阵;12为连杆2相对于连杆1坐标的变换矩阵;23为连杆3相对于连杆2坐标的变换矩阵;34为足端位置相对于连杆3坐标的变换矩阵;04为足端位置相对于基坐标的变换矩阵。
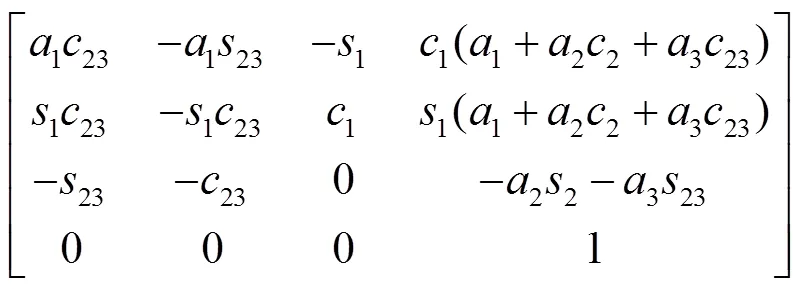
式中1sin1;2sin2;1cos1;2cos2;23sin(23);23cos(23)。
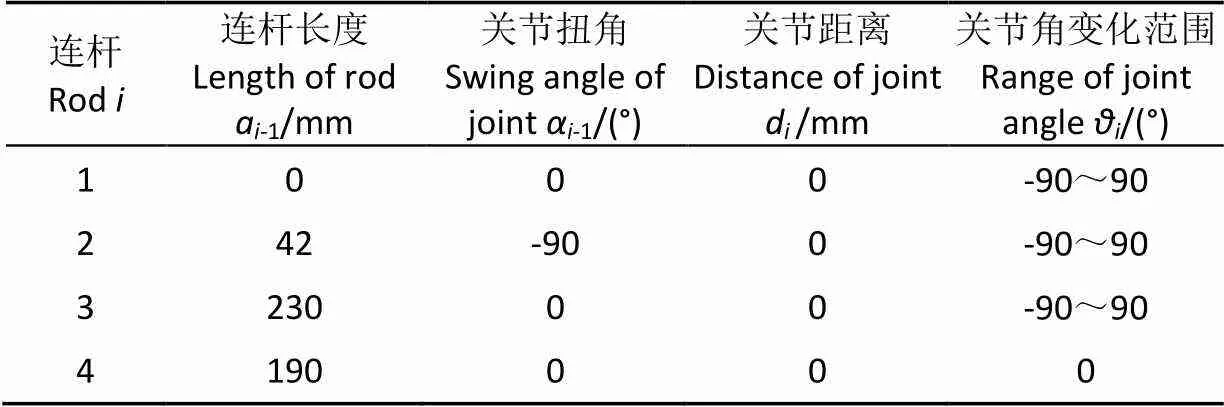
表1 四足移动平台前腿与后腿的D-H坐标参数
1.3 逆运动学分析
由于四足移动平台每条腿有3个自由度,所以在逆运动学方程求解时存在多解,因而采用齐次矩阵反变换法[21]来求解四足移动平台单腿逆运动学方程。根据其运动学正解方程等于四足移动平台足端位置矩阵,设四足移动平台足端位置齐次矩阵为
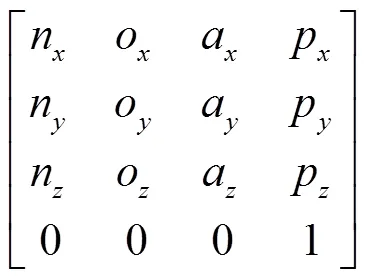
式中n、n、n表示相对于基坐标系的法线矢量元素;o、o、o表示相对于基坐标系的方向矢量元素;a、a、a表示相对于基坐标系的接近矢量元素;p、p、p表示相对于基坐标系的原点矢量元素。
根据运动学正解矩阵(2)与足端位置矩阵式(3)对应相等建立等式方程(4),求解各关节旋转角度θ(=1,2,3)。
04=(4)
将(01)-1和(12)-1左乘式(4)两端,根据矩阵方程两端对应元素相等得出
侧摆关节转角
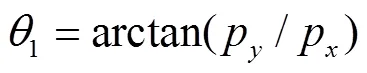
小腿关节转角
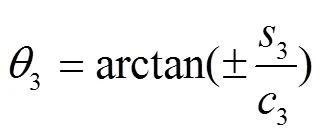
式中“+”表示后小腿关节转角,“−”表示前小腿关节转角;3((pc1+ps1−1)2+p2−22−32)/223;3。
大腿关节转角
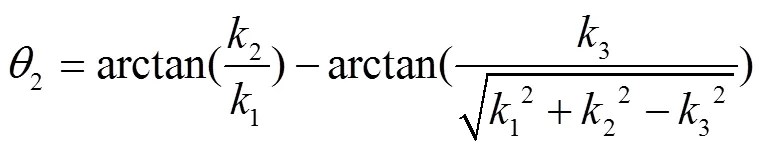
式中1=ps1+pc1−1;2=−p;3=33。
2 立体坡面姿态控制向量理论分析
当四足移动平台在立体坡面行走时要经过俯仰、横滚2个维度进行调整,因此在规划非线性足端轨迹的基础上,通过一维俯仰与二维横滚姿态向量的分析,得出立体坡面姿态变换向量,建立其机身姿态角与各腿关节转角的变换方程。
2.1 非线性足端轨迹设计
为减小四足移动平台的足端在与地面接触时产生的振动,采用分段五次多项式的足端轨迹规划[22]。根据边界条件:1)足端在摆动相开始和结束时速度与加速度均为零。2)足端起始位置为关节角在零位时的初始值。可得足端位置矩阵的原点矢量相对于基坐标的轨迹方程为

式中p、p和p为足端运动相对于基坐标0、0、0轴方向的起始位置;0为初始时刻足端侧向运动的初速度,m/s;1为初始时刻足端向后运动的初速度m/s;t、t、t分别表示相对于基坐标的足端位置处于不同相位时的表示时间,s;为步行周期,s;1、2和为足端在一个运动周期时相对于基坐标系的方向位移,mm。
摆动相:当运动时间≤/2时,t与t等于(s);当≤/4时(抬腿),t等于,/4≤/2时(落腿),t等于(/2)−。支撑相:当/2≤<时,t、t与t分别等于−。
2.2 一维俯仰姿态向量分析
如图3a所示,当四足移动平台处于一维俯仰坡面坡度为1(四足移动平台在前进时,机身上扬为正值)时,机身与坡面平行。在全局坐标系中,其重心轴线较中心轴线的偏置距离Δ为
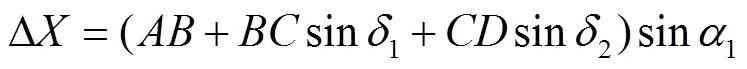
式中为侧摆连杆长度,mm;为大腿连杆长度,mm;为小腿连杆长度,mm;1为俯仰坡度,(°);1与2分别为大腿连杆与机身及小腿连杆与大腿连杆的延长线组成的角度,(°)。
为使四足移动平台的机身与全局坐标系轴保持平行,以前腿为例(如图3b所示),需要对机身以机身中心坐标系Y轴做俯仰旋转1,则前腿足端相对于基坐标系0和0轴的变化方程为
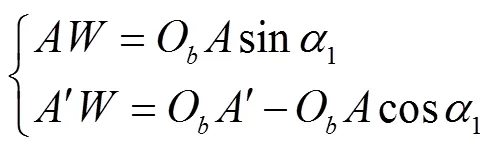
式中OA或OA'为四足移动平台机身长度的1/2。
此时,前腿基坐标系较初始位置下降了距离,相当于足端位置高度增加了,机身水平前移了距离,相当于足端水平向后移动了距离。后腿变换方式与前腿相同,但变换方向相反。
如图3c所示,将变换后的姿态按照机身坐标X轴平移Δ,得到新的变换姿态1111,使机身重心到前、后腿的足端平面投影位置相等。
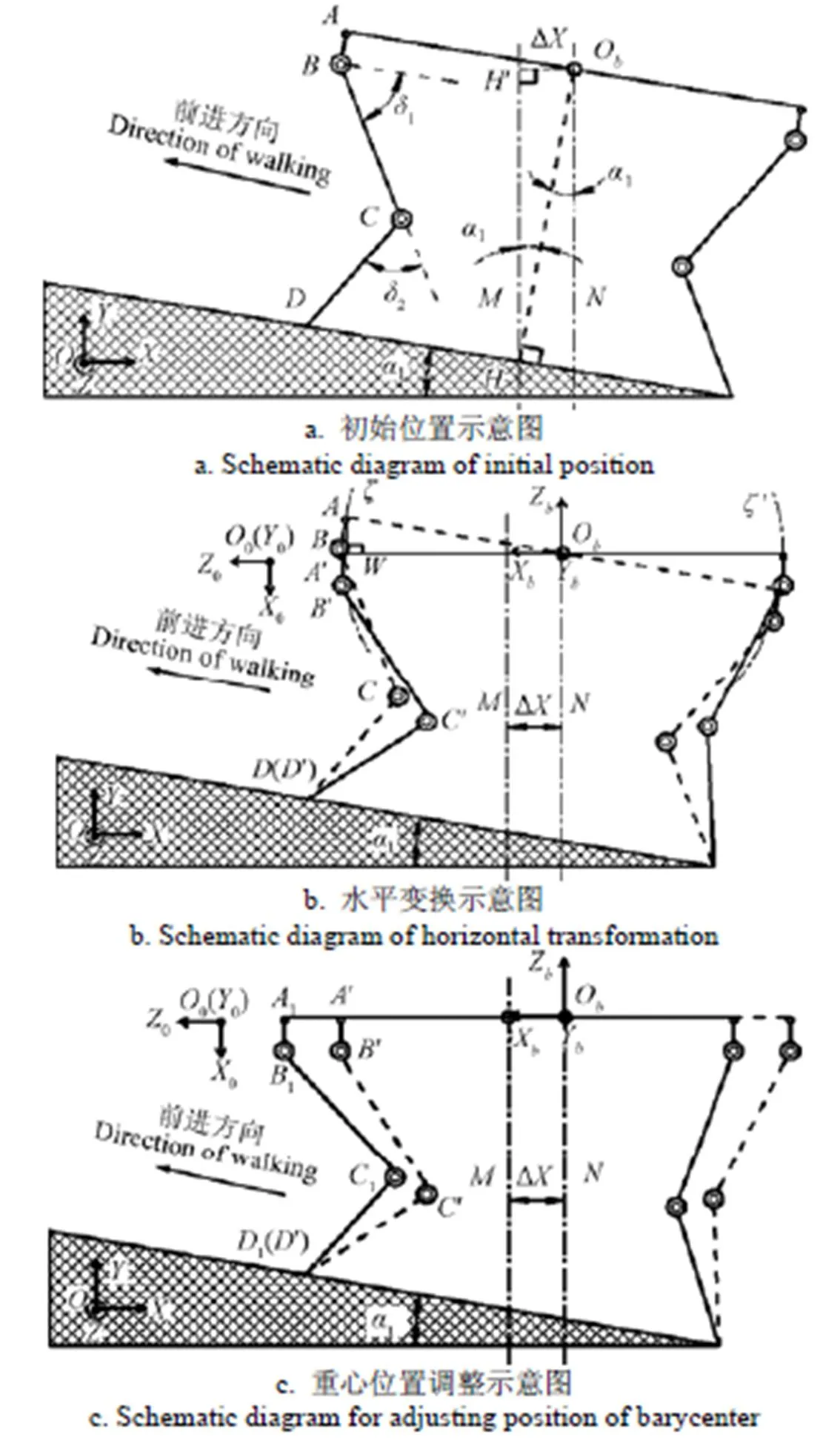
注 :OXYZ为全局坐标系;ObABCD为四足移动平台前端部分;轴线M、N为俯仰坡面足端中心线和机身重心所在直线;线段ObH为机身到俯仰坡面的中垂线,垂足为H;ObH'表示M轴与N轴间的距离ΔX,mm;ObXbYbZb为机身坐标系;ObABCD与ObA'B'C'D'表示在水平变换时机身姿态变换前后的机身位置;ζ和ζ '分别表示以ObA为半径绕机身坐标系Yb轴旋转的前后腿基坐标圆弧轨迹;A1B1C1D1为四足移动平台俯仰变换后最终姿态;δ1与δ2分别为大腿连杆BC与机身及小腿连杆CD与大腿连杆BC的延长线组成的角度,(°)。
将式(9)、(10)带入式(8),且p、p和p及0、1为0时,得到了四足移动平台在俯仰坡面运动时,足端位置矩阵相对于基坐标的原点矢量1=[p1p1p1]T,对应各元素方程表示为
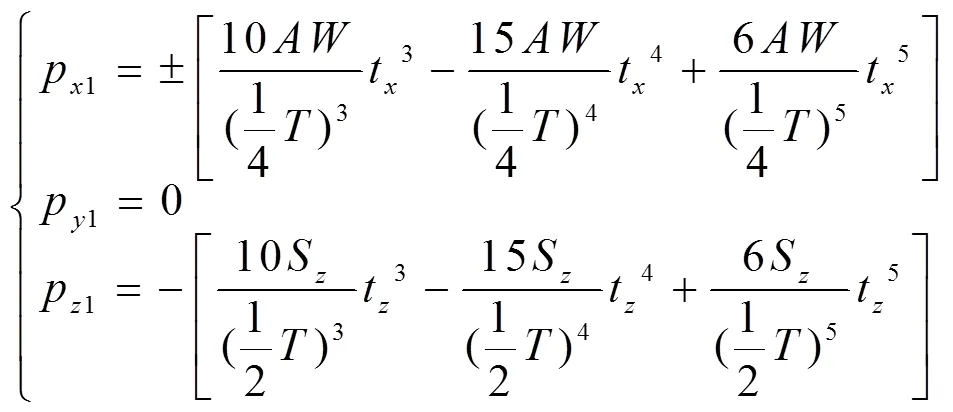
式中p1表示俯仰姿态变换时足端相对于基坐标0轴方向的位移,mm,其中“+”、“−”表示后腿、前腿变换,表示足端相对于全局坐标系方向的位移,mm;p1、p1表示俯仰姿态变换时相对于基坐标0、0轴方向的位移,mm;S=Δ±表示俯仰姿态变换时相对于全局坐标系方向的位移,mm,其中“+”、“−”分别表示前腿、后腿足端沿基坐标0方向位移。
足端相对于基坐标在0方向上的初始位置补偿为±,其中“+”表示足端沿基坐标向下,“−”与其相反。当四足移动平台为下坡时,前、后腿变换方式类似,但变换方向相反。
2.3 二维横滚姿态向量分析
当四足移动平台处于二维横滚坡面时如图4a所示,横滚坡度为2(此时为正值),前进方向沿全局坐标系轴正向运动(以左腿部分为例)。四足移动平台重心所在轴线较足端平面的中心轴线偏置Δ可表示为
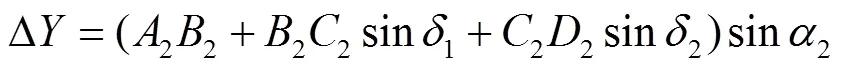
式中22为侧摆连杆长度,mm;22为大腿连杆长度,mm;22为小腿连杆长度,mm;2为横滚坡度,(°)。
从图4a中可以看出,为使四足移动平台的机身姿态与全局坐标系轴保持水平,需要对其机身(KOA2)以机身坐标系X轴横滚2变换到K'OA2a,则左腿足端相对于基坐标系0、0轴的变化方程为
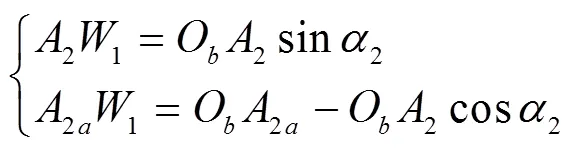
式中OA2或OA2a为四足移动平台机身宽度的1/2。此时,左、右腿基坐标系较初始位置的变化情况与2.2节类似。
如图4b所示,在机身姿态经水平变换后,为了使四足移动平台重心位置轴线与中心位置轴线重合,需要对其机身相对于全局坐标系轴平移。
将式(12)式(13)带入式(8),且p、p和p及0、1为0时,得到左、右足端位置矩阵相对于基坐标的原点矢量2=[p2p2p2]T,对应各元素方程表示为
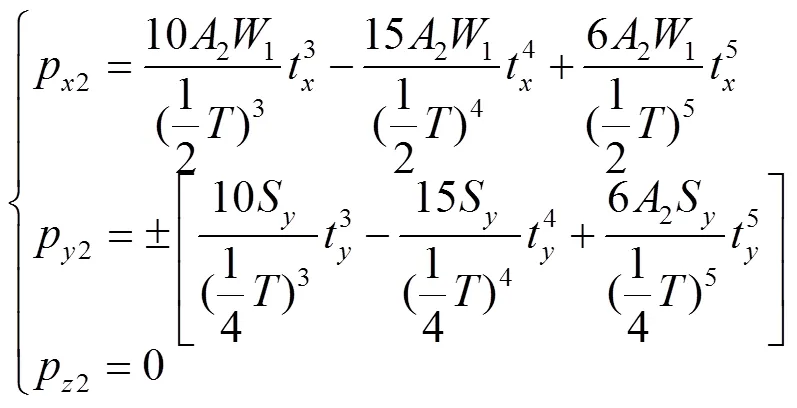
式中p2表示横滚姿态变换时相对于基坐标0轴方向的位移,mm,其中“+”表示右腿变换;“−”表示左腿变换;21表示足端相对于全局坐标系方向的位移,mm;p2、p2表示横滚姿态变换时相对于基坐标0、0轴方向的位移,mm;S=Δ±2a1表示横滚姿态变换时相对于全局坐标系方向的位移,mm,其中“+”、“−”分别表示左腿、右腿足端沿基坐标0方向位移。
注: 轴线1、1为横滚坡面机身重心轴线与足端中心轴线;线段OV为机身到横滚坡面的中垂线,垂足为;、表示以O为圆心,OA2为半径的圆弧;Δ为机身重心轴线1与足端中心轴线1的距离,mm;KOA2222为初始姿态;K'OA2a为横滚坡面水平变换姿态;1为2点到2a的投影点;2222与2222分别为移动平台在横滚坡面的初始位置及变换的最终位置;点画线部分表示机身水平变换后左侧部分位置。
Note: The axis1and1are the barycenter axis of body and the central axis of the foot end on the rolling slope;OVis the perpendicular bisector from the body to the rolling slope,is pedal;andare the arc withOA2as the radius andOas the center; Δisthe distance between the barycenter axis1of body and the central axis1of the foot end, mm;KOA2222is the initially attitude;K'OA2ais the attitude after horizontal transformation on the rolling slope;1is the projection point from2to2a;2222and2222are the initially position and the finally position of the mobile platform after transformation on the rolling slope; The part of stipple line are the left part of the body after the horizontal transformation.
图4 横滚坡面姿态变换示意图
Fig.4 Schematic diagram of attitude transformation on rolling slope
足端相对于基坐标在0方向上的初始位置补偿为±21,其中“+”表示足端沿基坐标向下,“−”与其相反。当横滚坡面角度2为负时,左、右腿变换方式相同,但变换方向相反。
2.4 立体坡面姿态向量分析
根据2.2及2.3的推导,把式(11)、式(14)带入到式(3),得到一维俯仰姿态足端轨迹1及二维横滚姿态足端轨迹2共2个足端位置齐次矩阵。先对机身做俯仰姿态变换,再进行横滚姿态变换,则四足移动平台立体坡面姿态足端轨迹矩阵为3=1×2。因此,当四足机器人处于三维坡面行走时,得到足端位置矩阵相对于基坐标的原点矢量3=[p3p3p3]T,对应各元素方程表示为

式中表示俯仰姿态变换下的足端法线矢量、方向矢量、接近矢量的3×3矩阵变换,各元素数值为俯仰姿态关节转角代入式(2)对应各元素数值;p3、p3、p3分别表示立体坡面姿态变换时相对于基坐标0、0、0轴方向位移,mm。
将(15)式各元素方程带入式(5)、式(6)、式(7),即得出其立体坡面机身姿态角与各腿关节转角的变换方程。
3 四足移动平台的步态规划
由于四足移动平台在平面行走时需要保持一定速度,坡面行走时需要减小速度来提高坡面行走稳定性与负载性能。因此,四足移动平台在平面行走时采用Trot步态[23-26],立体坡面行走时采用Walk步态。
3.1 平面Trot步态的规划
为提高四足移动平台以Trot步态在平面行走时的稳定性,采用改变支撑相足初始位置的方法[27]对其进行规划设计。设支撑足初始支撑位置相对于足端直线轨迹前端的位置系数为=/,且∈[0,0.5],(mm)为单腿跨距,(mm)为支撑足初始后移距离。当四足同时移动距离为时,其机身前进了位移,即相对于传统Trot步态支撑足初始后移距离。图5为平面Trot步态变化示意图。
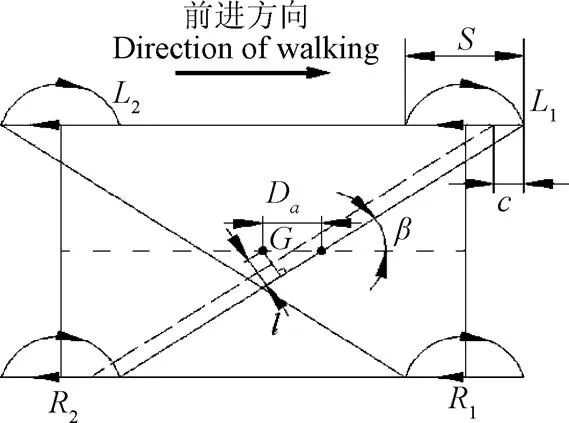
注: β为四足移动平台前进方向与支撑足对角线方向的夹角,(°);G为其重心所在位置;L1、L2、R1、R2分别为其足端位置;S为单腿跨距,mm;c为支撑足初始后移距离; Da为机身中心前移距离,mm;l为机身中心在支撑面上的投影到支撑对角线的垂直距离,mm。
如图5所示,当四足移动平台以Trot步态在平面行走时,机身重心在地面的投影不在支撑足所形成的支撑对角线上,造成移动平台绕支撑轴的横滚,进而影响运动的稳定性[28]。因此,根据欧拉动力学方程[29]Mgl=+×,得到
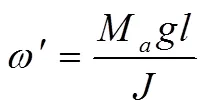
式中M为四足移动平台总质量,kg;为重力加速度,m/s2;为四足移动平台绕支撑对角线的转动惯量,kg·m2;为四足移动平台绕支撑对角线的角加速度,rad/s2;为机身中心在支撑面上的投影到支撑对角线的垂直距离,mm。其中,()为四足移动平台的行走速度关于运动时间的函数
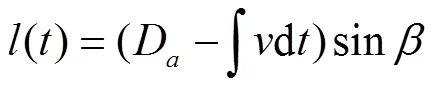
式中D=(0.5);为四足移动平台行走速度,m/s。
将式(17)带入式(16)后,对进行关于时间的2次积分得到横滚角(°)
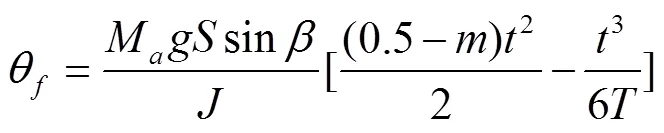
一般情况下,平面Trot步态的占空比为0.5,因此,取=0.5,则横滚角度可表示为
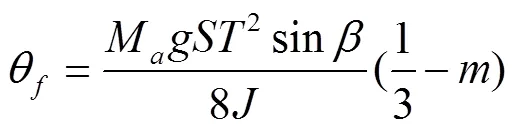
从式(19)可以看出:1)当在1/3附近取值时,其横滚角近似为0,步态规划后的占空比为/(1)。
2)横滚角与3成正比,由于=,根据SLIP理论[22],其行走最低速度应满足
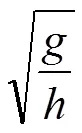
式中为四足移动平台质心距地面的高度,mm;为四足移动平台在支撑腿离地的瞬间质心的位置到中心平衡位置的距离,mm。因此在保证移动平台行走速度一定的情况下,步行周期越小越好。
3.2 立体坡面Walk步态的规划
四足移动平台立体坡面行走采用Walk步态,能够保持三条腿支撑坡面,提高机身在立体坡面行走时的稳定性。如图6(1)所示,如果四足移动平台进入立体坡面后有一条腿抬起,机身重心的位置在其余三足所组成的支撑三角形斜线附近,易引起横滚。因此,如图6(2)需要在其内部求取最优稳定点,当1处于摆动时,122构成三角形,并将点调整至最大稳定裕度点,称Δ122为次优三角形,其最大稳定裕度点为该三角形的内心。根据次优支撑三角形内稳定裕度理论进行分析[23],得到四足移动平台在立体坡面行走时的侧向平移p公式。

式中w为左右腿间距离,mm;l为前后腿间距离,mm。
当四足移动平台进入爬坡阶段时,先调平机身姿态,再按如图6所示的步态时序进行坡面行走。
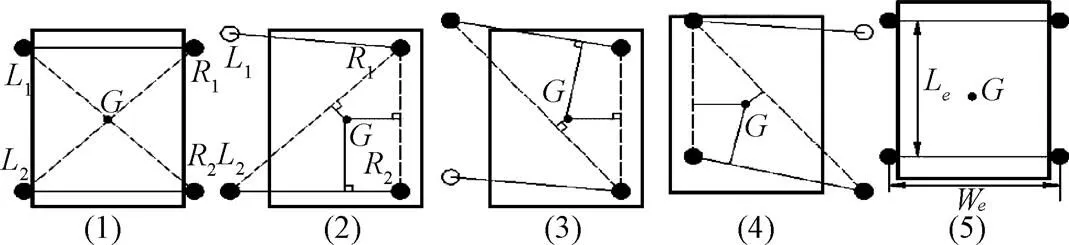
注 :G表示机身重心;黑点、空心圆分别表示支撑足与摆动足;图(1)~图(5)分别表示Walk步态的起始、左前腿运动、左后腿运动、右前腿运动及回位时序图。
4 立体坡面姿态理论与坡面行走仿真试验
为验证立体坡面姿态控制向量策略和步态规划的可行性,采用Matlab/SimMechanics模块进行理论测试及Matlab-Adams进行坡面行走仿真分析。
四足移动平台各部件尺寸依据常州迪华科技中心设计的四足机器人的0.4倍对所建立模型参数进行设置(如表2所示)。其中大腿连杆与机身、大腿连杆延长线与小腿连杆组成的锐角1和2分别为60°。立体坡面角度为(俯仰角度为±10°、横滚角度为10°)。
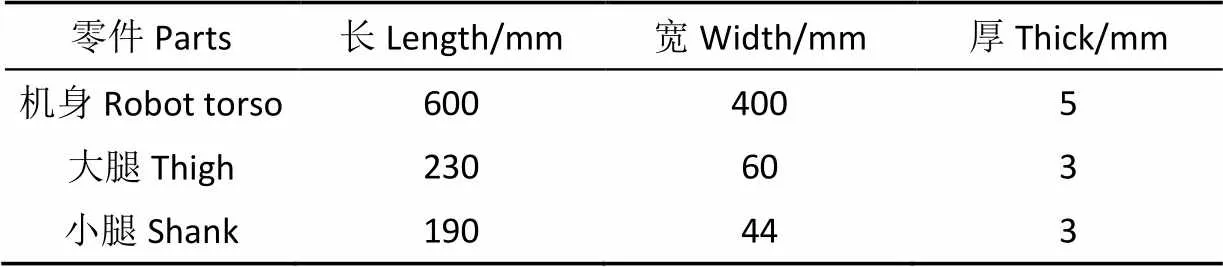
表2 四足移动平台结构参数
4.1 立体坡面姿态理论仿真分析
根据上述理论测试四足移动平台机身运动姿态角与其腿部各关节转角的变化规律,采用Matlab/Stateflow并根据2.4节推导编写立体坡面姿态控制器程序,同时利用Matlab/SimMechanics模块搭建四足移动平台的简化模型进行仿真测试。
用斜坡响应信号作为立体坡面机身变化角对立体坡面姿态理论的输入信号,测其各关节转角的变化情况,观察机身姿态是否水平,仿真时间为10 s,仿真步长设置为0.01 s。仿真过程如图7所示。
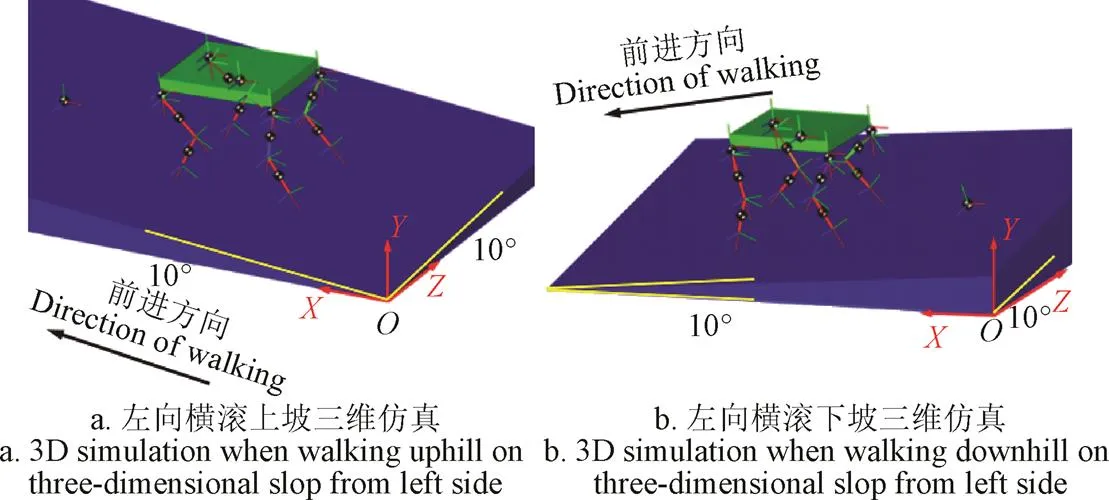
图7 Matlab/SimMechanics仿真截图
当机身与面平行时记录仿真测试结果。得到四足移动平台姿态角与腿部关节转角的理论仿真曲线、曲面(以左前大、小腿关节为例)如图8所示。

注: 图8a、8b为图7b时的结果;图8c表示横滚坡度为零时图7a的结果;图8d表示俯仰坡度为零时图7a的结果。
从图8可看出,当俯仰、横滚姿态角变化范围分别在±1°~±2°、±1°~±4°时,四足移动平台各腿关节转角变化较小,之后则关节转角变化较为明显。因此采用俯仰、横滚姿态角在±3°、±4°作为限定最小角度。当四足移动平台在行走时的机身姿态变化超过限定最小角度2个Trot步态周期时,先做姿态变换,再进行步态切换(Trot到Trot步态),可保证步态切换平稳。
4.2 坡面行走仿真试验分析
四足移动平台坡面行走仿真试验采用Matlab与Adams联合仿真模式[30-31]。坡面步态仿真试验参数按照上述理论及文献[32]合理选取如表3所示。

表3 四足移动平台虚拟样机仿真参数
注: Walk步态的行走速度符合SLIP理论,因此选择单腿跨度与Trot步态一致,占空比取5/6,步态周期为Trot的4倍;仿真时间以开始爬坡为分界点。
Note: The walking speed is consistent with the SLIP theory, so we choose the span distance of single leg of walking gait is same as the Trot gait and the duty cycle is 5/6. The walking gait cycle is 4 times of Trot gait. And the simulation begin at the demarcation point of slope.
采用Matlab/simulink编写驱动程序并对四足移动平台虚拟样机进行坡面行走仿真测试,观察从平面到坡面行走时的姿态变化过程。仿真结果如图9所示,由图9a可知,四足移动平台在0~6 s时处于平面行走状态,机身俯仰角与横滚角均保持在−2°~2°之间;在6~11 s时处于上坡阶段,机身俯仰姿态角开始增大,且在3°~4°范围连续变化,共有6段峰值。在12 s开始进行俯仰坡面行走,机身的运动姿态保持稳定。四足移动平台下坡行走仿真如图9b,仿真结果与俯仰上坡仿真一致。
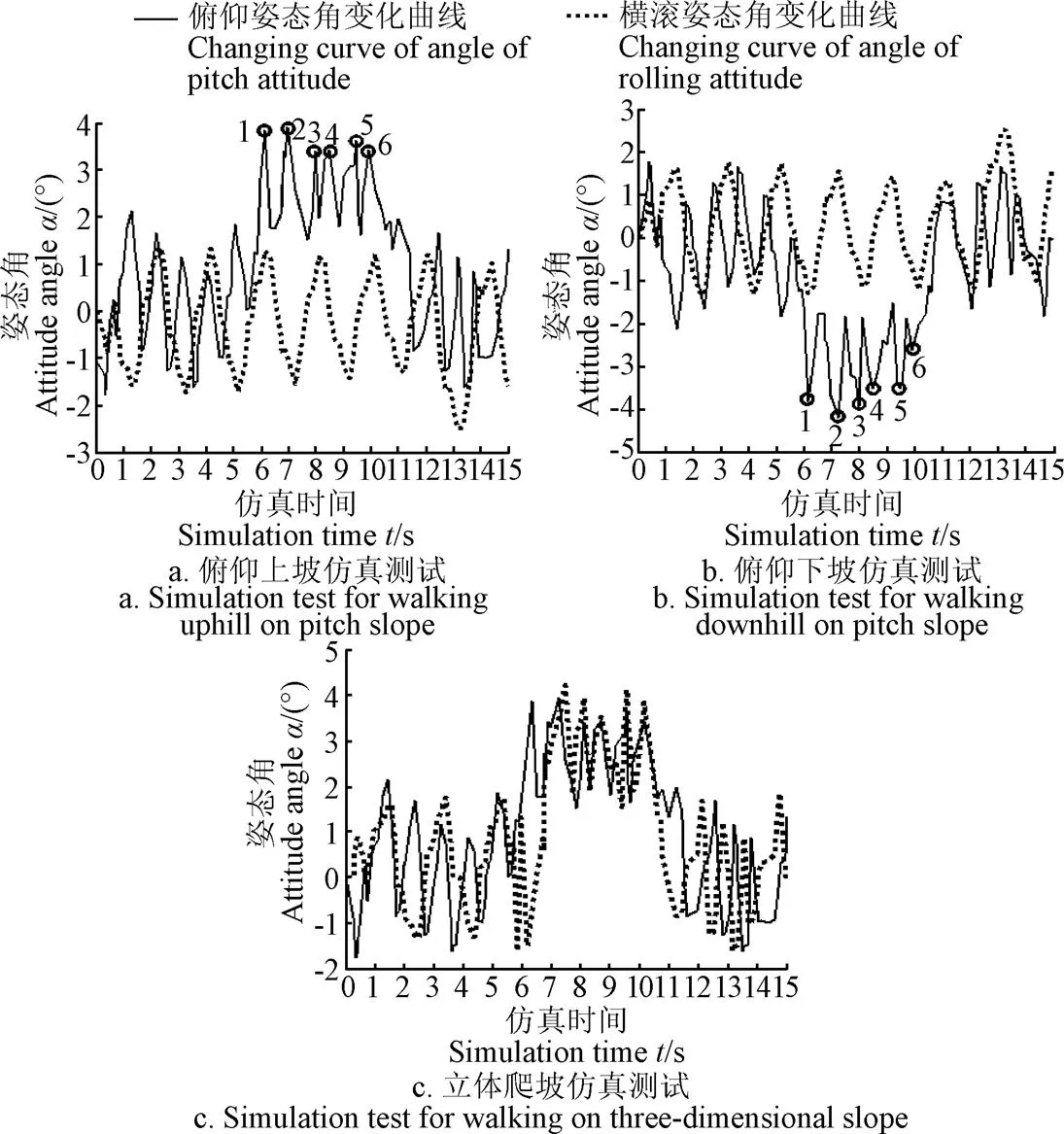
注: 图中标有1~6表示峰值点。
图9c为立体爬坡仿真测试,从开始至6 s时处于俯仰姿态变换,在7 s时横滚坡度到达4°,其俯仰、横滚姿态角同时连续变化,俯仰角变化峰值共有6段,横滚角变化峰值共有5段,且平面、立体坡面行走过程较平稳。
通过Matlab-Adams进行四足移动平台虚拟样机联合仿真试验,验证了2.4节建立的立体坡面姿态变换方程与平面Trot步态、坡面Walk步态规划及步态参数选取的可行性,得到了四足移动平台在上、下坡行走时的机身俯仰角曲线与横滚角度曲线,为物理样机试验测试提供了理论依据。
5 物理样机试验研究
为验证上述理论对农业四足移动平台在坡面行走时的工作性能,根据Solidworks所建立的三维模型制成工程图,利用东北农业大学工程实训中心对物理样机进行加工制造,并在中国黑龙江省农业机械工程科学研究院的室内土槽中进行调试与试验,以模拟四足移动平台作为农业移动辅助平台在农田的作业情况。其结构参数如表2所示,步态参数的选择与仿真一样。
5.1 控制系统介绍
当农业四足移动平台在平面及坡面行走时,控制系统根据姿态传感器采集当前的机身姿态变化角度,对其腿部关节进行角初始位置补偿,以保持机身水平,提高四足移动平台的作业平稳性。
四足移动平台物理样机控制系统采用上、下位机结构。计算机作为上位机,Arduino(UNOR3)作为下位机。用Simulink/Support Package for Arduino Hardware模块定义了Arduino(UNOR3)控制板各个引脚的输入与输出,通过串口通讯连接方式使Matlab与Arduino(UNOR3)之间实现数据传递;伺服电机驱动采用STM32F103芯片模块,可将转角信号转换成PWM脉宽信号驱动伺服电机;伺服电机采用KST-BLS825,扭矩30 kg·cm,用来驱动四足移动平台腿部关节,其旋转范围为±135°;姿态传感器采用君悦智控-MPU6050型六轴采集模块,姿态测量精度 0.01°,能够准确输出四足移动平台当前姿态。
5.2 俯仰姿态角与关节转角变化关系测试
如图10所示为物理样机在俯仰上坡时机身姿态角与关节转角的变化关系测试,验证所设计立体坡面姿态变换方程的有效性,将物理样机放在木板上,木板的前端用航车吊起,另一端用量角器测量木板与地面间的角度。调整挂起位置,使之每按一下控制按钮,其坡度值变化一度,并让木板逐渐抬起。当物理样机在测试俯仰下坡的变化情况时,则调整情况与上坡时相反。
将旋转姿态传感器分别安装在前大腿关节、前小腿关节、后大腿关节以及后小腿关节处,并依次变化木板与地面之间的角度,其中上坡、下坡角度变化范围分别为3°~10°和−3°~−10°。

1. 关节转角测试仪 2.量角器
试验中,对上、下坡面姿态对应的前大腿关节、前小腿关节、后大腿关节和后小腿关节共分8组进行,每组试验重复3次取平均数并记录试验数据如图11所示。
由图11可知,当机身俯仰姿态角在5°~7°及−5°~−7°时,试验值与理论值开始出现误差,其试验值与理论值的最大误差值为2.96°。产生误差的原因主要有:1)零件加工尺寸存在误差;2)对旋转角度传感器传回的数据进行滤波、修正处理存在调整偏差。但试验值与理论值变化趋势基本一致,验证了立体坡面姿态变换方程的有效性。
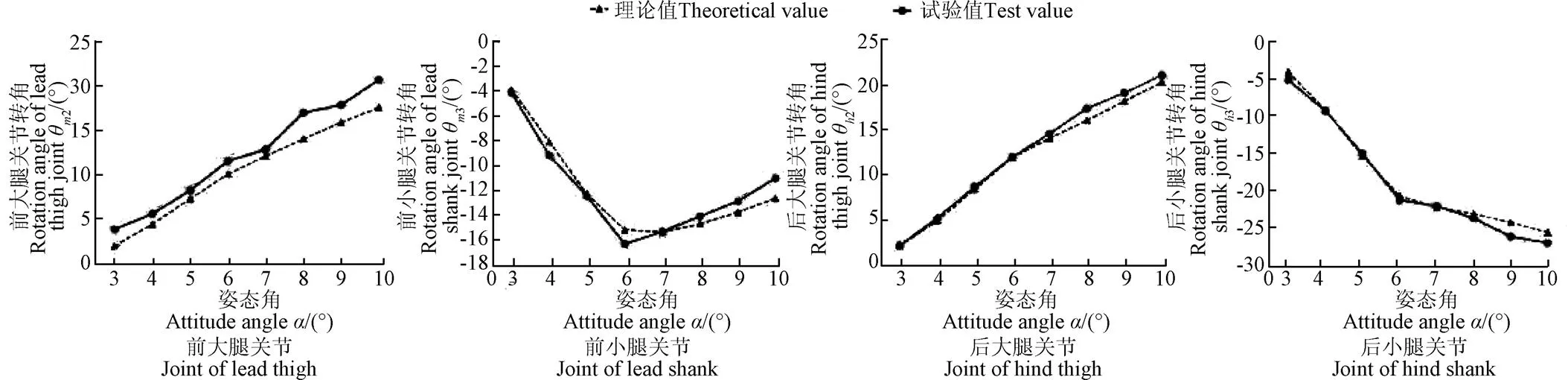
a. 上坡时腿部关节转角变化
a. Changing of rotation angle of legs joint on uphill
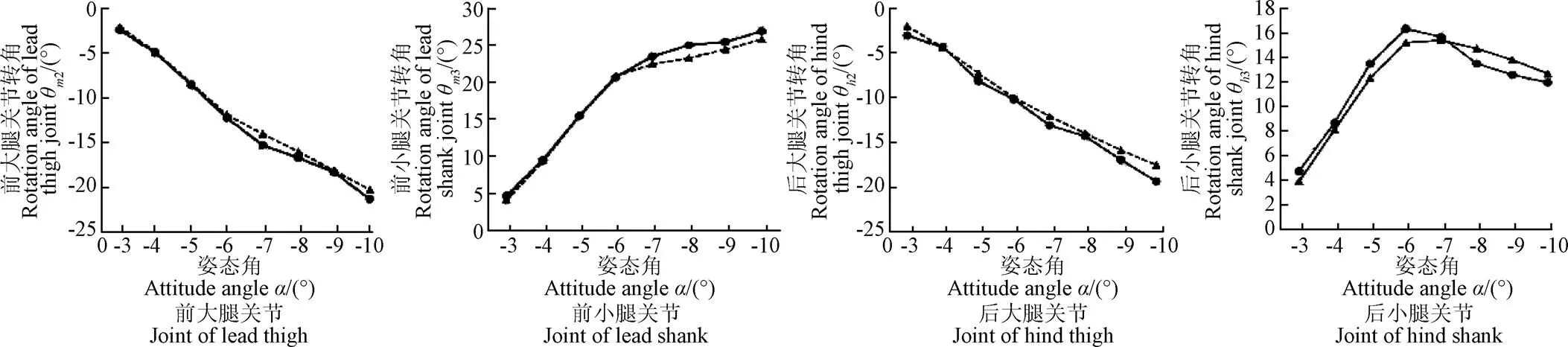
b. 下坡时腿部关节转角变化
5.3 立体坡面姿态行走测试
为研究农业四足移动平台在坡面行走时的姿态稳定性,如图12所示对四足移动平台物理样机进行俯仰、立体坡面姿态行走测试。试验步态参数与仿真一致,俯仰坡面角度分别为±10°,立体(俯仰、横滚坡面角度)为10°。通过试验观察,物理样机在坡面行走时能够对机身姿态做连续水平调整,步态运行平稳。同时,根据姿态传感器记录下物理样机在上、下坡面及立体坡面行走时的机身俯仰角度和横滚角度。图13为俯仰角度与横滚角度试验曲线。

图12 坡面姿态行走试验
如图13a所示为四足移动平台物理样机在俯仰上坡时的姿态角度变化曲线,从图中可以看出,物理样机从开始到5 s处于行走状态,机身俯仰角与横滚角保持在−2°~2°之间变化,在运行5~10 s处于上坡状态,俯仰姿态角在2°~5°之间连续变化,且峰值共有6段,当四足移动平台运行到11~15 s时,其俯仰姿态逐渐恢复到开始阶段,机身姿态保持水平。图13b为物理样机在俯仰下坡行走时的姿态变化曲线,移动平台从开始到3 s处于行走状态,在3~8 s处于下坡状态,8~15 s处于下坡行走状态,其姿态变化过程与俯仰上坡行走测试一致。
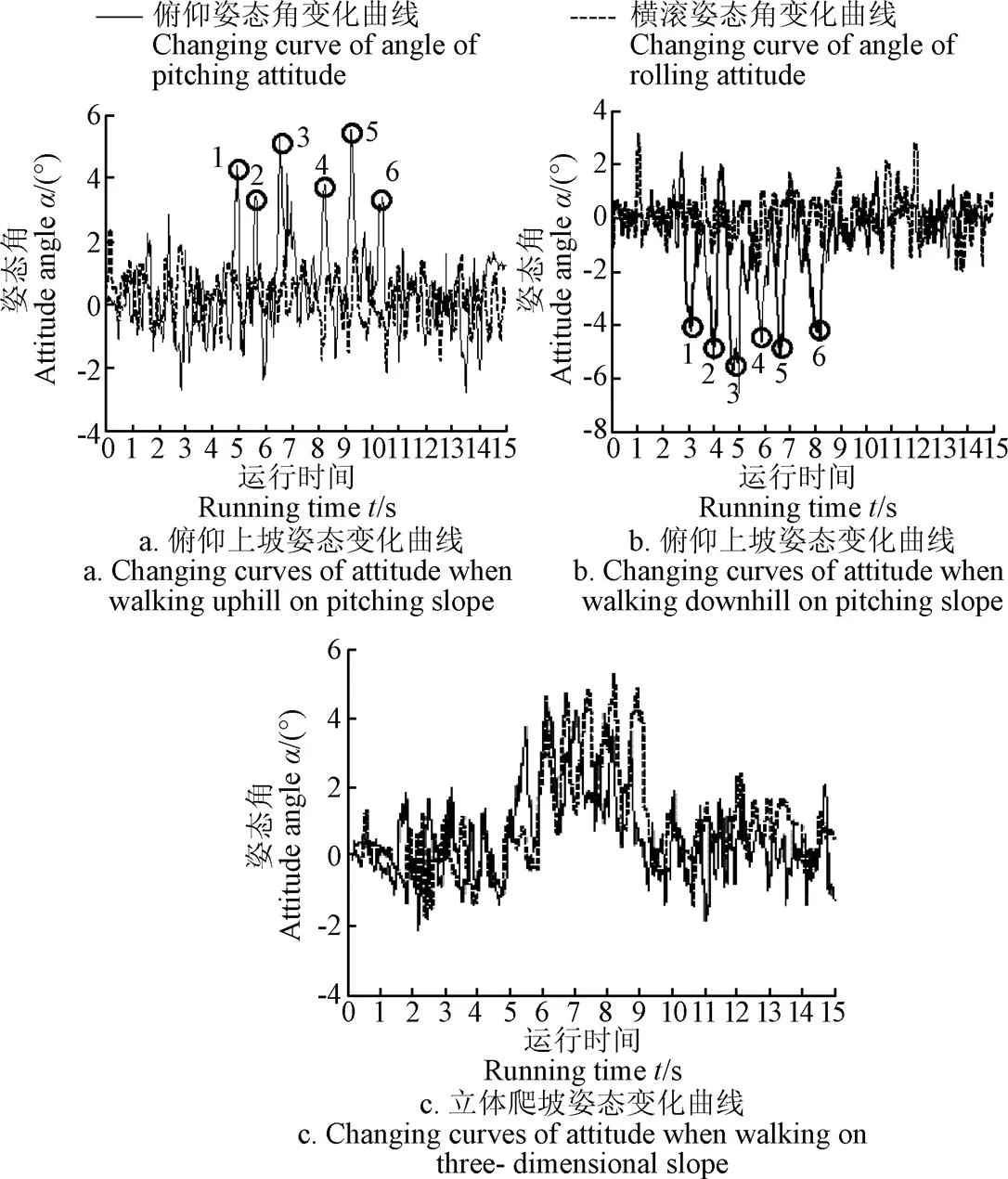
注: 图中标有1~6表示峰值点。
图13c所示为物理样机在立体坡面爬坡姿态角度变化曲线,从开始至5 s时处于俯仰姿态变换,在6 s时横滚坡度到达4°时,机身俯仰、横滚姿态角同时连续变化,俯仰峰值共有6段,横滚峰值共有5段。进入坡面后,其姿态运行较为平稳,试验结果与仿真基本一致。
由于土槽路面土壤颗粒较大,造成物理样机在行走时出现滑动,但可由控制器进行微调,使物理样机在平面、坡面行走时机身姿态角的变化幅度与仿真基本一致,验证了立体坡面姿态变换方程及其步态规划的合理性。
5.4 坡面负载平稳性测试
农业四足移动平台作为农业移动机械的辅助平台,在田间作业时,需要具备一定的负载平稳性。因此,验证所设计的四足移动平台负载性能试验关键在于有、无姿态控制时的负载质量随坡度变化的相对负载误差作为评价指标。其计算公式为

式中为相对负载误差,%;为无姿态控制坡面行走时的负载质量,kg;′为姿态控制坡面行走时的负载质量,kg;max为负载总质量,kg。
首先测试其静承载能力,将四足移动平台物理样机处于站立姿态,同时将玉米逐渐放入平台上。当伺服电机出现振动时,测其质量作为最大静承载能力。然后分别对Walk与Trot步态作行走承载测试,每组分10次。测试过程是先将四足移动平台加载到最大静承载质量,通过其Walk与Trot步态行走时,逐步取出玉米,直到伺服电机无振动时停止,同时记录其剩余负载质量。测试结果如图14所示。
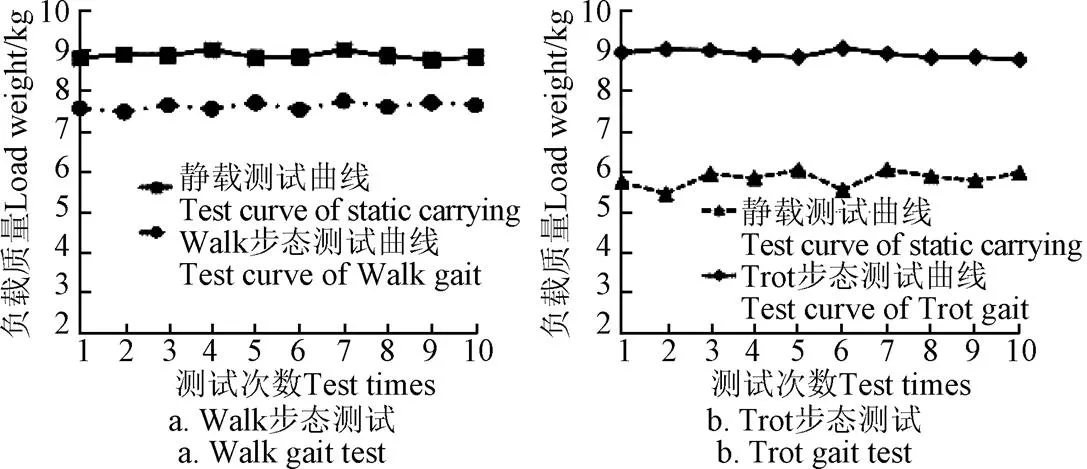
图14 承载能力测试曲线
将每组的试验结果取平均数,分别得到最大静承载质量范围在8.89~8.92 kg,Walk步态承载质量约为7.63 kg,Trot步态承载质量约为5.83 kg。
坡面负载平稳性测试应根据Trot步态的承载能力并考虑测试误差等因素,选择质量约为5 kg的玉米作为物理样机的负载行走测试目标,在土槽中对坡面分别板垫起俯仰角度为4°、6°、8°、10°以及俯仰和横滚为10°的立体坡面。
试验包括有、无姿态控制下的平地、俯仰上、下坡和立体坡等负载行走平稳性测试,试验共分10组,每组试验重复10次,将每组测得的试验数据分别取平均数并记录,结果如表4所示。
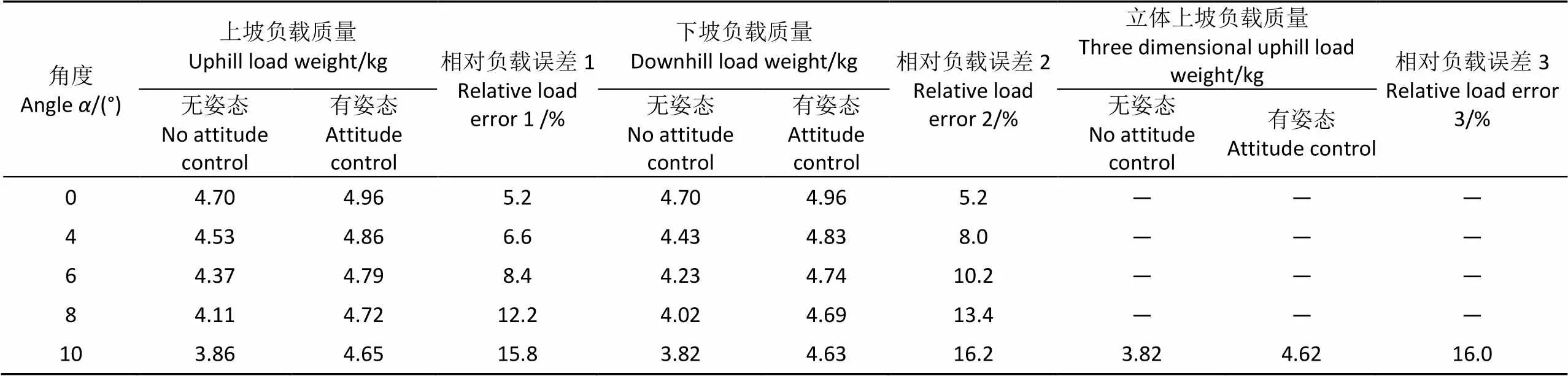
表4 坡面负载行走平稳性测试结果
注:0°时四足移动平台为正常平面行走。
Note: The quadruped mobile platform is walking on the flat surface when the slope is 0°.
由表4可知,平地行走时,四足移动平台物理样机在有姿态控制器比无姿态控制器的相对负载误差为5.2%。随着坡度的增加,四足移动平台负载相对误差逐渐增大。当上、下坡度为10°时,其上坡相对误差为15.8%,下坡相对误差为16.2%。在立体坡面行走时,其相对负载误差为16.0%,说明所设计的立体坡面姿态控制策略能够提高坡面行走时的负载平稳性能。
6 讨 论
1)本文是基于传统构型基础上进行立体坡面姿态分析研究,采用软件仿真与土槽试验相结合,验证了所提出的控制策略的合理性,实现了农业四足移动平台坡面运动姿态保持水平的目的,进而为后续对农业四足移动平台在田间不规则路面、坡面及更大坡度路面行走平稳性与提高负载质量(采用液压伺服驱动方式)等方面进行分析研究提供理论基础,对开展和探索新构型的农业四足移动平台具有参考意义。
2)本文根据机器人运动学原理对农业四足移动平台的立体姿态控制策略及步态规划进行研究,使其在立体坡面行走时,控制系统根据姿态传感器采集机身当前的姿态变化角度,对腿部关节进行角初始位置补偿来调整机身姿态,同时进行合理的步态选择,使机身的坡面行走姿态保持水平,提高行走平稳性、负载稳定性,是静力学、动力学分析的前提和基础。因此,后续将结合静力学、动力学分析农业四足移动平台的承载能力,深入研究农业四足移动平台在坡面行走时负载力与关节驱动力之间的变换关系并对机身平稳性的影响。该研究对四足移动平台在坡面行走时保持机身姿态水平,提高其负载平稳性等问题提供参考。
7 结 论
1)提出农业四足移动平台立体坡面姿态控制向量策略分析方法,在建立运动学模型基础上,通过对一维俯仰、二维横滚坡面姿态向量变化分析,得出其立体坡面机身姿态角与各腿关节转角的变换方程。
2)运用欧拉动力学方程、SLIP理论及次优支撑三角形内稳定裕度理论对四足移动平台平面Trot与立体坡面Walk步态进行规划,为其步态参数的选择提供了理论依据。
3)通过Matlab/SimMechanics的坡面姿态仿真试验,对所提出的控制策略进行研究,选择俯仰、横滚姿态变化的限定最小角度为±3°、±4°。Matlab-adams虚拟样机仿真试验,验证了立体坡面姿态变换方程、平面Trot步态及坡面Walk步态规划的可行性,得到了四足移动平台在10°的立体坡面行走时,其俯仰角与横滚角变化范围在−2°~2°。
4)进行农业四足移动平台物理样机进行机身姿态角与关节转角变化关系测试和立体坡面姿态行走试验,试验结果与仿真基本一致,验证了立体坡面姿态控制向量理论分析方法及其步态规划的合理性,实现了农业四足移动平台坡面运动姿态保持水平的目的,提高了坡面行走的稳定性;坡面负载平稳性能试验结果表明,在上、下坡及立体坡面的负载平稳性与无姿态控制器相比分别提高了15.8%、16.2%和16.0%,增强了四足移动平台作为农业移动辅助平台的作业性能。
[1] 赵匀,武传宇,胡旭东,等. 农业机器人的研究进展及存在的问题[J]. 农业工程学报,2003,19(1):20-24.
Zhao Yun, Wu Chuanyu, Hu Xudong, et al. Research progress and problems of agricultural robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2003, 19(1): 20-24. (in Chinese with English abstract)
[2] Avital Bechar, Clement Vigneault. Agricultural robots for field operations. Part 2: Operations and systems[J]. Biosystems Engineering, 2017, 153: 110-128.
[3] 荣誉,金振林,曲梦可. 三自由度并联机械腿静力学分析与优化[J]. 农业工程学报,2012,28(20):41-49.
Rong Yu, Jin Zhenlin, Qu Mengke. Statics analysis and optimal design of 3-DOF parallel mechanical leg[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(20): 41-49. (in Chinese with English abstract)
[4] 张金柱,金振林,陈广广. 六足步行机器人腿部机构运动学分析[J]. 农业工程学报,2016,32(9):45-52.
Zhang Jinzhu, Jin Zhenlin, Chen Guangguang. Kinematic analysis of leg mechanism of six-legged walking robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(9): 45-52. (in Chinese with English abstract)
[5] 牛雪梅,高国琴,刘辛军,等. 三自由度驱动冗余并联机构动力学建模与试验[J]. 农业工程学报,2013,29(16):31-41.
Niu Xuemei, Gao Guoqin, Liu Xinjun, et al. Dynamics modeling and experiments of 3-DOF parallel mechanism with actuation redundancy[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(16): 31-41. (in Chinese with English abstract)
[6] 纪超,冯青春,袁挺,等. 温室黄瓜采摘机器人系统研制及性能分析[J]. 机器人,2011,33(6):726-730.
Ji Chao, Feng Qingchun, Yuan Ting, et al. Development and performance analysis on cucumber harvesting robot system in greenhouse[J]. Robot, 2011, 33(6): 726-730. (in Chinese with English abstract)
[7] 李贻斌,李彬,荣学文,等. 液压驱动四足仿生机器人的结构设计和步态规划[J]. 山东大学学报:工学版,2011,41(5):32-36.
Li Yibin, Li Bin, Rong Xuewen, et al. Mechanical design and gait planning of a hydraulically actuated quadruped bionic robot[J]. Journal of Shandong University: Engineering Science, 2011, 41(5): 32-36. (in Chinese with English abstract)
[8] 柴汇,孟健,荣学文,等. 高性能液压驱动四足机器人SCalf的设计与实现[J]. 机器人,2014,36(4):385-391.
Chai Hui, Meng Jian, Rong Xuewen, et al. Design and implementation of SCalf, an advanced hydraulic quadruped robot[J]. Robot, 2014, 36(4): 385-391. (in Chinese with English abstract)
[9] 张皓然,戈振扬,于英杰,等. 除草用四足机器人稳定性的判定与分析[J]. 湖南农业大学学报,2015,41(3):340-344.
Zhang Haoran, Ge Zhenyang, Yu Yingjie, et al. Stability analysis and judging of the quadruped robot for weeding[J]. Journal of Hunan Agricultural University, 2015, 41(3): 340-344. (in Chinese with English abstract)
[10] 张皓然. 四足除草机器人的静态步行及稳定性研究[D]. 昆明:昆明理工大学,2015.
Zhang Haoran. Static Walking and Stability of a Quadruped Weeding Robot[D]. Kunming: Kunming University of Science and Technology, 2015. (in Chinese with English abstract)
[11] Sehoon Park,Yun-Jung Lee. Gait analysis of a quadruped walking robot with vertical waist-joint on slope[J]. Original Research Article IFAC Proceedings Volumes, 2009, 42(13): 507-512.
[12] 冯华山,王润孝,赵国斌,等. 四足机器人坡面静步态平衡方法研究[J]. 机械科学与技术,2009,28(4):436-441. Feng Huashan, Wang Runxiao, Zhao Guobin, et al. Abalance method for the Static Gait of a quadruped robot over a slope[J]. Mechanical Science and Technology for Aerospace Engineering, 2009, 28(4): 436-441. (in Chinese with English abstract)
[13] 韩宝玲,贾燕,李华师,等. 四足机器人坡面运动时的姿态调整技术[J]. 北京理工大学大学学报,2016,36(3):242-246.Han Baoling, Jia Yan, Li Shihua, et al. Posture adjustment for quadruped robot trotting on a slope[J]. Transactions of Beijing Institute of Technology, 2016, 36(3): 242-246. (in Chinese with English abstract)
[14] 孟健,李贻斌,柴汇,等. 连续不规则台阶环境四足机器人步态规划与控制[J]. 机器人,2015,37(1):85-93.
Meng Jian, Li Yibin, Chai Hui, et al. Gait planning and control of quadruped robots in continuous irregular steps environment[J]. Robot, 2015, 37(1): 85-93. (in Chinese with English abstract)
[15] Zhang X, Zheng H, Xu G, et al. A biological inspired quadruped robot: structure and control[C]//IEEE International Conference on Robotics and Biomimetics. IEEE, 2005: 387-392.
[16] Meek S, Kim J, Anderson M. Stability of a trotting quadruped robot with passive, underactuated legs[C]// IEEE International Conference on Robotics and Automation. IEEE, 2008: 347-351.
[17] 李冰,苏文海,息晓琳,等. 仿生四足机器人自适应粒子群优化控制[J]. 农机化研究,2018,40(5):24-29.
Li Bing, Su Wenhai, Xi Xiaolin, et al. Adaptive particle swarm optimization control of bionic quadruped robot[J]. Journal of Agricultural Mechanization Research, 2018, 40(5): 24-29. (in Chinese with English abstract)
[18] 蔡自兴. 机器人学[M]. 北京:清华大学出版社,2009.
[19] 权龙哲,彭涛,沈柳杨,等. 立体苗盘管理机器人的机械臂参数优化与试验[J]. 农业工程学报,2017,33(7):10-19.
Quan Longzhe, Peng Tao, Shen Liuyang, et al. Parameter optimization and experiment of manipulator for three-dimensional seedling tray management robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(7): 10-19. (in Chinese with English abstract)
[20] 权龙哲,张冬冬,查绍辉,等. 三臂多功能棚室农业机器人的运动学分析及试验[J]. 农业工程学报,2015,31(13):32-38.
Quan Longzhe, Zhang Dongdong, Zha Shaohui, et al. Kinematics analysis and experiment of multifunctional agricultural robot in greenhouse with three arms[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(13): 32-38. (in Chinese with English abstract)
[21] Paul R P. Robot manipulators: Mathematics, Programming, and Control: The Computer Control of Robot Manipulators[M]. Massachusetts: Richard Pual, 1981.
[22] 张志宇. 基于ADAMS的四足机器人虚拟样机仿真及刚柔耦合分析[D]. 哈尔滨:哈尔滨工业大学,2016.
Zhang Zhiyu. Virtual Prototype Simulation and Rigid- Flexible Doupling Analysis of Quadruped Robot Based on Adams[D]. Harbin: Harbin Institute of Technology, 2016. (in Chinese with English abstract)
[23] 王立鹏,王军政,汪首坤,等.基于足端轨迹算法的液压四足机器人步态控制策略[J].机械工程学报,2013,49(1):39-44.
Wang Lipeng, Wang Junzheng, Wang Shoukun, et al. Strategy of foot trajectory generation for hydraulic quadruped robots gait planning[J]. Journal of Mechanical Engineering, 2013, 49(1): 39-44. (in Chinese with English abstract)
[24] 丁庆鹏. 基于阻抗控制的四足仿生机器人稳定步态理论及实验研究[D]. 哈尔滨:哈尔滨工业大学,2016.
Ding Qingpeng. Theory and Experimental Research on Stable Gait of Quadruped Robot Based on Impedance Control[D]. Harbin: Harbin Institute of Technology, 2016. (in Chinese with English abstract)
[25] 韩晓建,商李隐,杨涌. 四足机器人启动步态设计及稳定性分析[J]. 机械科学与技术,2016,35(8):1169-1175.
Han Xiaojian, Shang Liyin, Yang Yong. Start gait design and stability analysis of a quadruped robot[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(8): 1169-1175. (in Chinese with English abstract)
[26] 谢惠祥,尚建忠,罗自荣,等. 四足机器人对角小跑中机体翻转分析与姿态控制[J]. 机器人,2014,36(6):676-682.
Xie Huixiang, Shang Jianzhong, Luo Zirong, et al. Body rolling analysis and attitude control of a quadruped robot during trotting[J]. Robot, 2014, 36(6): 676-682. (in Chinese with English abstract)
[27] 刘蕊,俞志伟,王鹏,等. 仿生四足机器人对角步态规划及稳定性分析[J]. 科学技术与工程,2013,13(36):10852-10856.
Liu Rui, Yu Zhiwei, Wang Peng, et al. Trotting gait planning and stability analysis for a biomimetic quadruped robot[J]. Science Technology and Engineering, 2013, 13(36): 10852-10856. (in Chinese with English abstract)
[28] 何冬青,马培荪,曹冲振,等. 四足机器人对角小跑起步姿态对稳定性的影响[J]. 上海交通大学学报,2005,39(6):880-883.
He Dongqing, Ma Peisun, Cao Chongzhen, et al. Effects of the initial stance of quadruped trotting on stability[J]. Journal of Shang Hai Jiao Tong University, 2005, 39(6): 880-883. (in Chinese with English abstract)
[29] 刘蕊. 基于力传感器的四足机器人多步态规划及初步维稳控制[D]. 南京:南京航空航天大学,2014.
Liu Rui. Mulit gait Planning and Preliminary Maintenance of Stability Controlling Based on Quadruped Robot With Force Sensor[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014. (in Chinese with English abstract)
[30] 王建明,赵彦,朱彦防,等. 基于ADAMS与MATLAB的四足机器人的trot步态联合仿真[J]. 机床与液压,2015,43(3):57-59.
Wang Jianming, Zhao Yan, Zhu Yanfang, et al. Coordinated simulation of trot gait for quadruped robot based on ADAMS and MATLAB[J]. Machine Tool and Hydraulics, 2015, 43(3): 57-59. (in Chinese with English abstract)
[31] 赵彦. 基于ADAMS和MATLAB的四足机器人联合仿真[D]. 济南:山东大学,2014.
Zhao Yan. The Simulation of Quadruped Robot Based on Matlab and Adams[D]. Jinan: Shandong University, 2014. (in Chinese with English abstract)
[32] Koopman B, van Asseldonk E H F, van der Kooij H. Speed-dependent reference joint trajectory generation for robotic gait support[J]. Journal of Biomechanics, 2014, 47: 1447-1458.
Strategy and experiment of attitude control for quadruped mobile platform walking on three-dimensional slope used for agriculture
Su Wenhai1, Li Bing1, Yuan Lipeng2, Zhang Hui2, Tan Hewen1, Xi Xiaolin1
(1.150030,; 2.150001,)
With the continuous improvement of modern agricultural automation technology, agricultural robots have become the new trend of agricultural machinery. As an auxiliary mobile platform of agricultural machinery, robots with feet have unique advantages compared with other mobile platforms and have been widely used in various fields of agriculture. The quadruped robot has the advantages of movement pattern of four-legged mammals and very strong adaptability and flexibility to complex terrain. Therefore, the quadruped robot has gradually become an magnet of new area. As an auxiliary mobile platform for agricultural machinery, the smooth motion posture of quadruped robot directly influence on its work performance when walking on a slope. In order to improve the stability and smoothness with load of the quadruped mobile platform while walking on the farmland, a vector control strategy of the three-dimensional slope is proposed in this paper. First of all, according to the structure, topological mode and parameters of each joint of the four-legged mobile platform, the coordinate transformation of the link of the leg is established and the kinematics is modeled. Based on the transformation relationship between the four-legged mobile platforms, the kinematic positive and inverse solutions are carried out, then the kinematic solution of the foot-end position and the leg joint angle of the four-legged mobile platform is achieved. The second, based on the kinematics model of quadruped mobile platform, the transformation equations between the angle of body and the swing angle of the leg joints on the three-dimensional slope were reduced, by analyzing the change of attitude vector on two-dimensional (pitch and roll) slope. Then, the Walk gait planning on three-dimensional slope and Trot gait planning on flat surface of the agricultural quadruped mobile platform were carried out, by using the Euler dynamic equation, SLIP theory and the stability margin theory of sub optimal support triangle. According to simulation result of slope attitude by Matlab/SimMechanics, we studied its control strategy, select pitch and roll attitude change as the limit of minimum angle. The third, the result of Matlab-adams virtual prototype simulation verify the practicability of this method about the three-dimensional attitude transformation equations and the gait planning. We can get the conclusion that the pitch and roll angle changes in the range of -2°−2°, when the mobile platform walking on the three-dimensional slope with pitch and roll are both 10°. The last, the walking experiment on three-dimensional slope was carried out. The experiment results were basically consistent with the simulation; This results verify the rationality of this three-dimensional slope attitude transformation equation and gait planning; This method not only achieve the aim of maintaining the upper platform on the level surface, but also improve the walking stability, when the quadruped mobile platform is walking on the slop; For the four-legged mobile platform load stability experiment, the static load capacity will be tested. According to the relative load error of load quality with slope changes with or without attitude control, and as an evaluation index, the results show that: The proposed attitude control strategy for slopes improves the load stability by 15.8%, 16.2% and 16.0% respectively compared with the non-attitude controller when walking on the upper and lower slopes or three-dimensional slopes. It enhanced the performance of four-legged mobile platform as the agricultural mobile . The performance of the auxiliary platform provides a reference for the design of the motion attitude control of the modern agricultural mobile platform.
agricultural machinery; control; algorithms; quadruped mobile platform; attitude angle; rotation angle of joint; slope attitude; gait planning
2017-09-08
2018-01-04
国家科技支撑计划项目(2013BAH57F01);国家自然基金青年科学基金项目(51205057)
苏文海,副教授,博士,主要从事机电智能控制及液压伺服特性的研究。Email:250577403@qq.com
10.11975/j.issn.1002-6819.2018.04.010
TP242.6
A
1002-6819(2018)-04-0080-12
苏文海,李 冰,袁立鹏,张 辉,谭贺文,息晓琳. 立体坡面农业四足移动平台姿态控制策略与试验[J]. 农业工程学报,2018,34(4):80-91.doi:10.11975/j.issn.1002-6819.2018.04.010 http://www.tcsae.org
Su Wenhai, Li Bing, Yuan Lipeng, Zhang Hui, Tan Hewen, Xi Xiaolin. Strategy and experiment of attitude control for quadruped mobile platform walking on three-dimensional slope used for agriculture[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(4): 80-91. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2018.04.010 http://www.tcsae.org

