DSMC计算中碰撞对取样和时间推进环节的高效处理方法
屈 程, 王江峰(1. 中国飞行试验研究院, 陕西 西安 710089; . 南京航空航天大学 航空宇航学院, 江苏 南京 10016)
0 引 言
DSMC方法是Bird从流动的物理模拟出发发展的一种直接模拟蒙特卡洛方法[1],是模拟过渡领域真实气体流动问题最成功的方法之一[2-5]。然而,DSMC方法的较大缺点是其对较高密度稀薄流问题的模拟能力不强,并且计算耗时太长,这大大限制了该方法的大规模应用。为克服上述缺点,研究者们发展了多种方法,如采用多线程并行计算[6-7]、设计高效率分子搜索算法[7]、更改DSMC方法中的数据结构[8]、引入碰撞距离思想[9-10]、发展自适应当地时间步长方法[11-12]等。
DSMC方法中,计算网格起两种作用[13]。第一种是对流场宏观流动参数进行空间离散,第二种是促进碰撞分子碰撞对的选择,使其满足基本的几何接近。为了保证模拟结果的正确性,DSMC数值模拟中需要保证网格尺寸不超过当地分子平均自由程的三分之一。高超声速稀薄流场中激波区域密度相对较大,分子平均自由程相对较小,而其它区域密度相对较低,分子平均自由程相对较大,在数值模拟过程中很难保证全流场满足上述网格尺寸要求[10];同时,为了对密度相对较大的区域有较高的平均自由程和碰撞频率的分辨率,流场时间步长必须取得非常小,这会降低流场整体计算效率[11]。
为了放宽DSMC方法对网格尺寸的限制,文献[7]在选择分子碰撞对时引入了碰撞距离的思想,预先给定分子碰撞距离,以第一个分子的位置为圆心(或球心),以碰撞距离为半径做圆(或球),在分子所在网格与圆(或球)的公共区域选择第二个分子,该方法在每次分子碰撞对选择时都需要进行公共区域判定及区域内模拟分子标记,这必然会带来较大的计算消耗。文献[10]将自适应碰撞距离的思想引入虚拟子网格方法,能够避免上述处理带来的计算消耗,但是该文献采用常数作为分子碰撞对选取的最大循环次数,常数值过小会对计算精度造成影响,而过大又会降低计算效率;并且,当循环结束仍未找到满足要求分子碰撞对时,该文献直接采用随机选择的分子对进行碰撞处理,这会降低较疏网格情况下的计算精度。本文发展了一种基于自适应碰撞距离的分子碰撞对选取方法,能够在程序中动态设定适合于每个网格单元的分子碰撞对最大循环次数,同时对于循环结束仍不能找到满足碰撞距离要求分子碰撞对的情况也做了针对性处理。
为了加快流场的时间发展历程,研究者们发展了自适应当地时间步长方法,通过构造流场探测器,在流场计算中动态更新每个网格单元内的时间乘数因子Ti,网格单元i内的模拟分子在Ti倍基时间步长间隔内只处理一次。本文结合自适应当地时间步长方法和DSMC方法数据结构特点,发展了一种自适应分子时间步长方法,能够以模拟分子为最小时间步长调整单位,为其分配适当的时间步长。
1 计算方法
1.1 DSMC方法介绍
DSMC方法使用大量的模拟分子模拟真实的气体,用一个模拟分子代表一定数量的真实气体分子,整个模拟中分子之间以及分子和物面之间不断进行能量交换,在充足的模拟时间后,通过采样统计得到每个网格的宏观流场结果[14-15]。本文采用非结构贴体网格,计算中采用可变硬球(Variable Hard Sphere,VHS)分子模型,采用恒温边界条件,物面采用完全漫反射条件,使用Larsen- Borgnakke唯象论模型处理模拟分子间的能量交换。
1.2 自适应碰撞距离碰撞对选取方法
为了在保证计算精度的同时降低DSMC方法对网格尺寸的限制,本文引入碰撞距离的思想,发展了一种自适应碰撞距离的分子碰撞对选取方法,网格单元i中的自适应碰撞距离di由下式确定:
di=min(Hi,ref,λi/3)
(1)
其中,Hi,ref为网格单元i的特征尺寸,λi为单元i中的局部分子平均自由程,数值模拟过程中每隔400步对网格单元i中的λi和di进行一次更新,式(1)使碰撞距离限制在三分之一局部自由程之内。
分子碰撞对选取的主要处理步骤如下:
1) 给定碰撞对中第二个分子选取的最大循环次数pi=max[1,int(NUMi/2)],其中NUMi为网格单元i中的模拟分子数,集合{1,2,3...,NUMi}中的每个正整数对应网格单元i中的一个模拟分子;
2) 首先在集合{1,2,3...,NUMi}中随机选取一个正整数,并找到与之对应的模拟分子M;
3) 采用步骤2中的方法随机选取第二个模拟分子L,计算并存储M和L之间的距离dML;
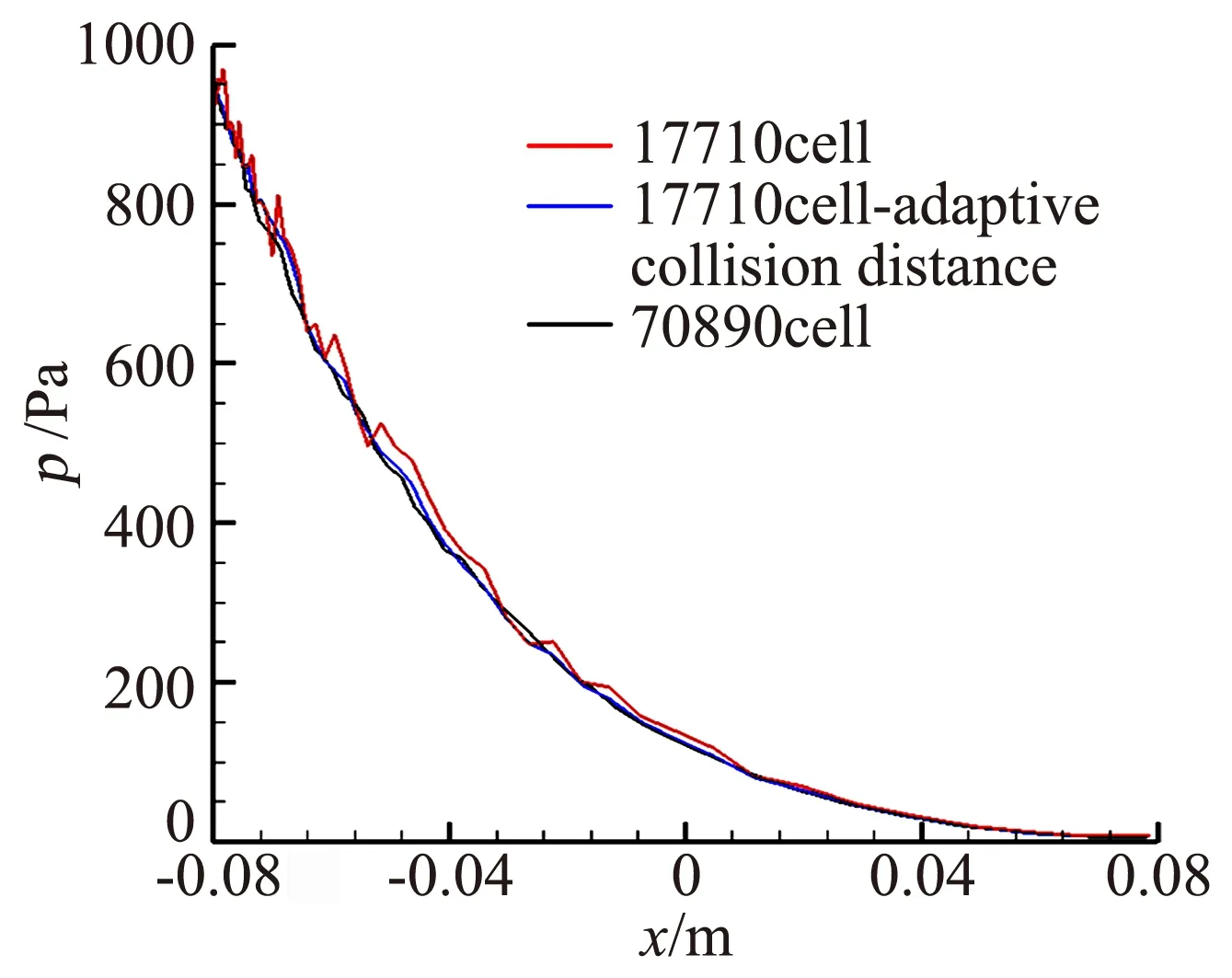
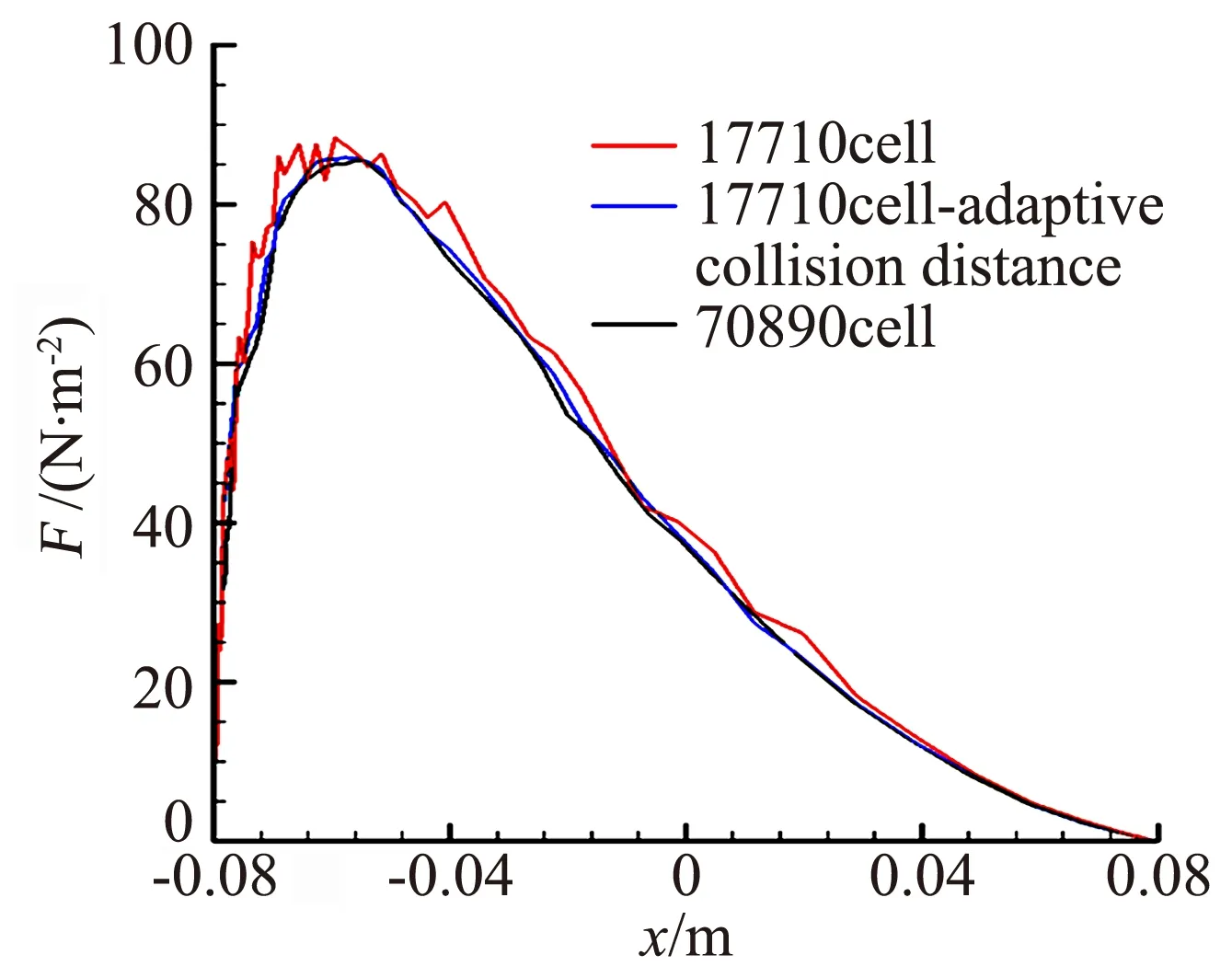
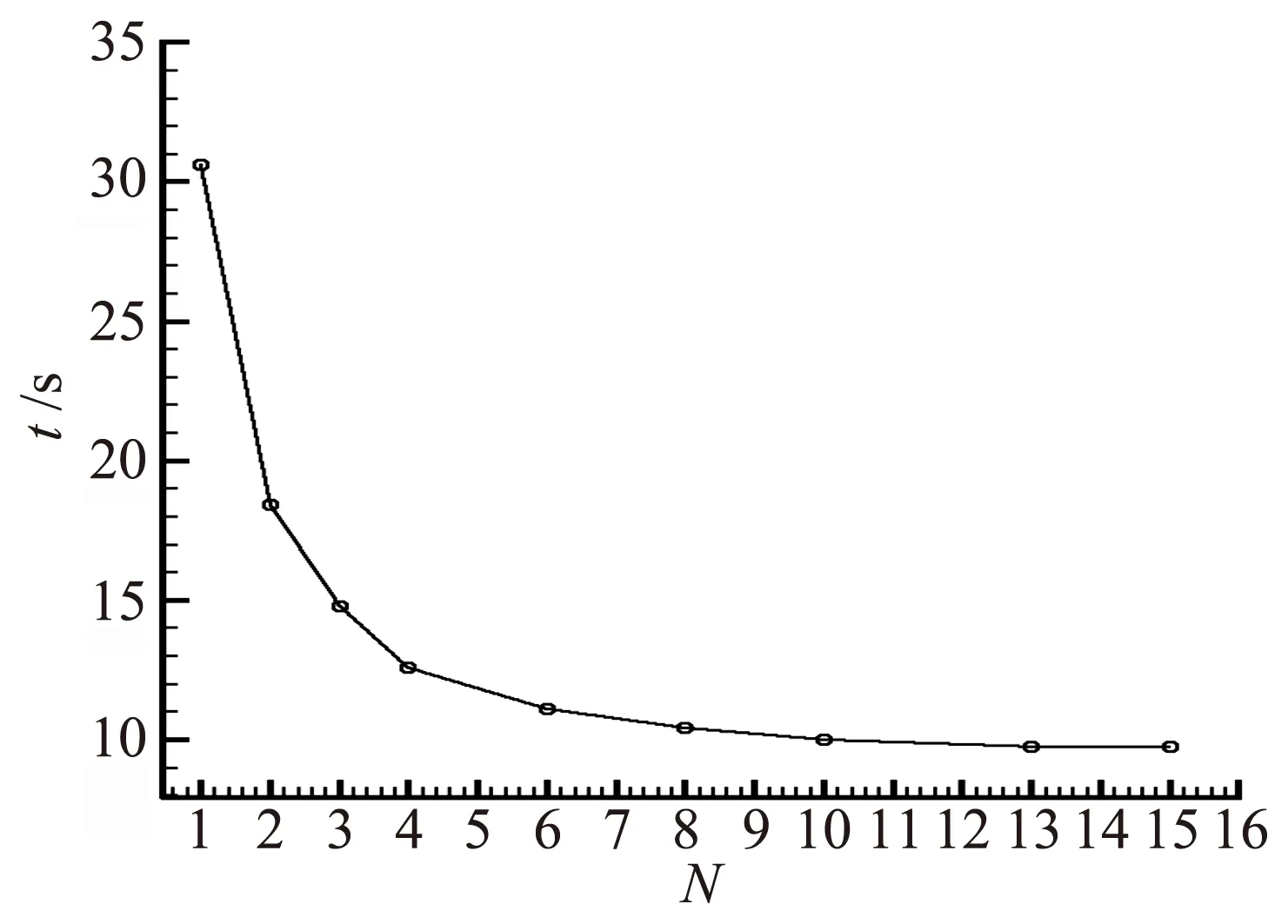
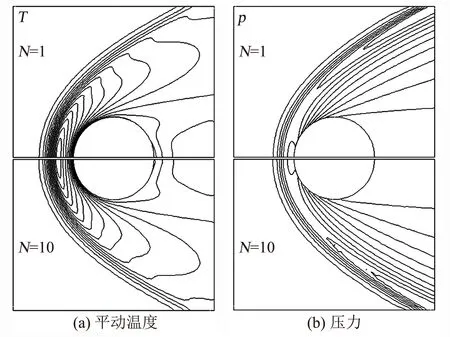
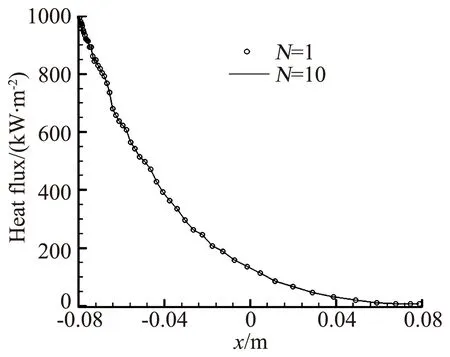
4) 判断0 上述处理步骤中采用与网格单元i中分子数相关的max[1,int(NUMi/2)]作为碰撞对中第二个分子选取的最大循环次数,采用这种方式能够获得较高的碰撞对选取效率,引入max()函数是为了保证循环顺利进行。步骤4中,达到pi次循环后仍未找到满足需求的分子时,直接选取循环过程中距离M最近的分子与之构成分子碰撞对,这样处理可以在尽量满足计算精度的同时保证计算效率。 采用DSMC方法进行流场模拟时,需要记录每个分子的性质信息,包括速度、内能、位置、所在网格单元以及分子组分等。经过分析可以发现,如果在DSMC模拟中额外存储每一个分子的时间乘数因子信息,并参照自适应当地时间步长的思想,利用分子速度大小和与分子所在网格单元相关的特征长度构造时间乘数因子,则可以发展出一种以模拟分子为最小时间步长调整单位的自适应分子时间步长方法,主要思想如下: 首先定义模拟分子所在网格单元的特征长度: Hk,locate,ref=min(Hi,ref,λi/3) (2) 特征长度与1.2节中的自适应碰撞距离大小一致,同样随流场宏观参数变化而改变。这样可以保证自适应分子时间步长方法和自适应碰撞距离碰撞对选取方法的兼容,且适用于较疏网格。 调整编号为k分子的时间乘数因子Tk需要确定3个参数:最大允许时间乘数因子N,各分子初始时间乘数因子Tk,0,以及基时间步长Δt。最大允许时间乘数因子由人为设定,初始时间乘数因子设定为1,本文基时间步长选取由下式决定: (3) 其中,Href为网格单元的等效尺寸,V∞为来流速度,V∞为来流分子碰撞频率。 k编号分子的时间乘数因子Tk的调整方法为: 1) 保存当前的时间乘数因子,Tk,old=Tk; 2) 由分子速度大小Vk及分子所在单元特征长度Hk,locate,ref,确定其适合的时间乘数因子Tk,id= int(Hk,locate,ref/(VkΔt)),若Tk,id 如果当前时间步Nk,t满足mod(Nk,t,Tk)=0,则开始处理编号为k的分子,该分子下一次运动和碰撞的时间步长Δtp通常可以简单地表示为Δtp=TkΔt,但由于分子可能在下一次被处理前已经产生时间乘数因子的更新,此时Δtp≠TkΔt,因此,分子k下一次运动的时间步长可以表示为Δtp=[mod(Nk,t,Tk,old)+Tk,new-mod(Nk,t,Tk,new)]Δt,即为时间乘数因子调整以前剩余的运动时间步长mod(Nk,t,Tk,old)Δt和时间乘数因子调整以后的剩余时间步长[Tk,new-mod(Nk,t,Tk,new)]Δt之和。 DSMC方法的本质是在近似小的时间步长内,将分子的运动和分子间的碰撞进行解耦,采用自适应分子时间步长方法时,同一个单元内不同编号分子的时间乘数因子不尽相同,在Nk,t时间步、i单元中只有满足mod(Nk,t,Tk)=0的分子才进行了运动模拟,因此,不能直接采用NTC法对i单元中的所有分子进行碰撞对取样,需要作出适当调整,本文的做法是在每个基时间步都对i单元中满足mod(Nk,t,Tk)=0的分子进行标记和数目统计,根据满足上述条件的分子计算碰撞数,并在其中进行分子碰撞对选取,通过上述方式保证单元中碰撞频率与实际一致。 采用不同网格尺寸下的圆柱外形对发展的自适应碰撞距离分子碰撞对选取方法进行了计算分析。圆柱半径R=0.08 m,来流气体摩尔百分比为N2∶O2=0.763∶0.237,分子数密度为n=3.84×1020/m3,来流速度7500 m/s,来流温度为Tinf=186 K,物面温度为Twall=1000 K,采用统一时间步长。 为了对自适应碰撞距离碰撞对选取方法进行验证,本文选取了两种不同尺寸的非结构网格进行了计算分析:第一种为较密的网格(物面附近网格尺度为来流分子平均自由程的六分之一,远场网格尺度为来流分子平均自由程的三分之一),网格单元数为70890;第二种为较疏的网格,网格单元数为17710。对第二种网格分别采用自适应碰撞距离方法与不采用该方法两种工况进行了计算分析。 图1、图2和图3分别给出了两种网格尺寸下物面热流、压力以及摩阻分布,从中可以看出,17710个单元的较疏网格在采用自适应碰撞距离方法后能够得到与70890个单元的较密网格符合较好的物面热流、压力以及摩阻分布结果,不采用自适应碰撞距离方法的较疏网格与较密网格结果吻合得相对较差,圆柱外形算例表明本文发展的自适应碰撞距离碰撞对选取方法能够一定程度放宽DSMC方法对网格尺寸的限制,在相对较疏的网格下取得相对令人满意的结果。 图1 不同网格下物面热流密度分布Fig.1 Heat flux on the surface at different grid sizes 图2 不同网格下物面压力分布Fig.2 Pressure on the surface at different grid sizes 图3 不同网格下物面摩阻分布Fig.3 Friction on the surface at different grid sizes 以算例2中的圆柱外形为例,选用网格单元数为17710的较疏网格,在采用自适应碰撞距离碰撞对选取方法的基础上,进行采用自适应分子时间步长方法和采用统一时间步长的对比计算,基时间步长取为2×10-7s,计算条件与算例2保持一致,流场模拟分子总数趋于稳定后约为28万。对比计算是在一台配置为Intel(R) Core(TM)2 2.80GHz,2.00GBRAM的微机上进行,运动和碰撞模拟共进行100000步,流场参数统计进行1000步。 图4给出了采用不同最大时间乘数因子每执行100步运动和碰撞模拟所用时间的比较,N=1表示采用统一时间步长。从图4可以看出,随着N的增大,计算时间下降较快,当N>8时,计算时间趋于平稳,这主要是由于局部分子碰撞频率控制了局部分子时间步长的自适应过程,致使计算时间不能继续下降,该趋势与文献[7]一致。本算例中最大时间乘数因子取N=10的计算时间为3.12 h,采用统一时间步长的计算时间为8.92 h,加速比为2.86。因此,采用本文发展的自适应分子时间步长方法可以显著缩短模拟所需的计算时间。 图4 每100步计算时间比较Fig.4 Comparison of computing time every 100 steps 图5为采用统一时间步长(N=1)的结果和N=10的流场平动温度和压力等值线对比图,等值线图按完全相同的参数绘制,从图中可以看出,两种方法下流场等值线几乎完全一致。图6为N=1和N=10的物面压力和热流密度的对比图,同样符合很好。图5、图6表明采用本文发展的自适应分子时间步长方法对计算结果几乎不产生影响。 图5 不同最大时间乘数因子对流场结构影响的比较Fig.5 Comparison of field structure with different N (a) 压力 (b) 热流密度 本文研究了DSMC计算中的高效处理方法,在碰撞对取样环节引入碰撞距离的思想,发展了一种自适应碰撞距离的分子碰撞对选取方法;在时间推进环节以模拟分子为最小时间步长调整单位,发展了一种自适应分子时间步长方法。对圆柱外形验证算例的计算分析表明在DSMC计算中采用本文发展的高效处理方法能够在相对较疏的网格下得到与传统DSMC计算相一致的结果。本文的方法能够一定程度放宽DSMC方法对网格尺寸的限制,并且能够大幅度缩短流场达到稳定需要的计算时间。 [1]沈青. 稀薄气体动力学[M]. 北京: 国防工业出版社, 2003 [2]樊菁. 稀薄气体动力学: 进展与应用[J]. 力学进展, 2013, 43(2): 185- 201 [3]Boyd I D. Computation of hypersonic flows using the direct simulation Monte Carlo method[C]//21st AIAA Computational Fluid Dynamics Conference, San Diego, CA, June 24-27, 2013 [4]Qu C, Wang J F. Hybrid grid DSMC method for chemical nonequilibrium with rarefied flow heating[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2015, 32(4): 409-414 [5]Moss J N, Glass C E, Greene F A. DSMC simulation of Apollo capsule aerodynamics for hypersonic rarefied conditions[R]. AIAA 2006-3577 [6]Kim M G, Kim H S. A parallel cell based DSMC method with dynamic load balancing using unstructured adaptive meshes[R]. AIAA 2003-1033 [7]王学德. 高超声速稀薄气流非结构网格DSMC及并行算法研究[D]. 南京: 南京航空航天大学, 2006 [8]Matthias L. Optimization and parallelization of the DSMC method on unstructured grids[R]. AIAA 97-2512, 1997 [9]Lebeau G J, Boyles K A, Lumpkin F E. Virtual sub-cells for the direct simulation Monte Carlo method[R]. AIAA 2003-1031 [10]黄飞, 陈智, 程晓丽, 等. 一种基于自适应碰撞距离的DSMC虚拟子网格方法[J]. 空气动力学学报, 2014, 32(4): 506-510 [11]Matthias L. Local time stepping with automatic adaptation for the DSMC method[R]. AIAA-98-2670, 1998 [12]朱荣丽. 过渡区DSMC数值模拟的一种自适应当地时间步长新方法[J]. 宇航学报, 2008, 29(4): 1142-1146 [13]Gallis M A, Torczynski J R, Rader D J, et al. Convergence behavior of a new DSMC algorithm[J]. Journal of Computational Physics, 2009, 228: 4532- 4548 [14]Bird G A. Molecular gas dynamics and the direct simulation of gas flow[M]. Oxford: Clarendon Press, 1994 [15]陈伟芳, 吴明巧, 赵玉新, 等. 超声速平板绕流DSMC/EPSM混合算法研究[J]. 空气动力学学报, 2002, 20(4): 441-445.1.3 自适应分子时间步长方法
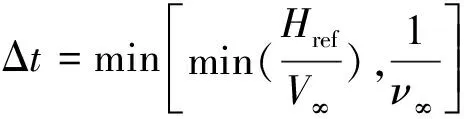
2 算例验证1:自适应碰撞距离碰撞对选取

3 算例验证2:自适应分子时间步长

4 结 论

