水下垂直发射航行体空泡流动研究
唐一华
(中国运载火箭技术研究院,北京 100076)
0 引言
水下垂直发射指航行体利用布置在水下运动平台上的垂直发射装置弹射入水后,依靠惯性在水中做无控运动,并以一定的速度穿越水面的过程。垂直发射与水平发射、倾斜发射方式相比,具有全方位攻击、装载量大等特点,是水下发射技术领域的重要发展方向。
在水下垂直发射过程中,航行体从运动的平台上发射出筒,经历水中航行、穿越自由液面后进入空中飞行,通常将整个运动过程分为出筒段、水中段和出水段3个阶段,水下垂直发射航行体运动过程见图1。出筒段,航行体从位于水下一定深度,并以一定速度运动的发射平台上实施发射,发射装置在航行体与发射筒之间的空间产生高温高压燃气,形成作用在航行体尾部的推力,使得航行体不断加速出筒进入水中,至航行体全部进入水中时,已经具有较高的运动速度;水中段,航行体无控制向上运动,受到阻力、浮力、重力等共同作用,轴向运动速度不断减小,同时受到平台牵连运动影响和法向力作用存在横向速度,在水动力矩作用下航行体姿态不断变化;出水段,航行体跨介质飞行,从头到尾依次穿越自由液面。

图1 水下航行体垂直发射运动过程Fig.1 Vertical launch process of the underwater vehicle
为了保证航行体出水后姿态,垂直发射航行体一般采用较高的水下运动速度。由于水介质绕流的作用,在航行体表面形成局部低压区,当压力小于水的饱和蒸汽压力时,航行体周围的水介质将汽化而产生附体空泡。同时,航行体离开发射筒后,筒内高温高压燃气附着在航行体尾部形成尾空泡。空泡流是水下垂直发射重要的流动现象之一,与航行体的运动过程密切相关,是水下发射技术研究的重点和难点。
1 水下垂直发射的特点与难点
同其他水下发射方式相比,由于发射的独特方式,水下垂直发射空泡流涉及的流动问题具有动基座发射、非定常流动、跨界面运动和多影响因素等4个方面的特点。
1.1 水下动基座发射
由于发射过程中发射平台存在一定的速度,并通过发射筒传递到航行体上,航行体在轴向运动的同时还存在横向运动,使得流体动力呈现出较为明显的不对称性,并对航行体的载荷和姿态造成显著影响。
1.2 非定常空泡流动
垂直发射航行体在水下高速运动时,附体空泡的产生与航行体的头型、来流速度、环境压力等因素密切相关。当航行体采用钝锥形头型时,易在肩部形成附体空泡;当航行体采用流线形头型时,流场结构比较稳定,只有在速度较高或环境压力较小的情况下才能形成空泡。一般用空化数σ来描述空化现象,其常见的表达形式为:

针对水下航行体而言,不断变化的运动条件与周围环境使得空泡流存在明显非定常现象,空泡整体尺度不断变化。研究表明,空泡流在外界扰动的作用下呈不稳定流动状态[1-4],空泡的非定常性常常表现为空泡自由表面的脉动及失稳、空泡非定常溃灭及其脱落。例如,图2(a)的空泡非稳定被限制在一个相对小的区域内,从大尺度范围来看是稳定的;而图2(b)是非稳定的局部空泡,其非稳定效应影响整个空泡。
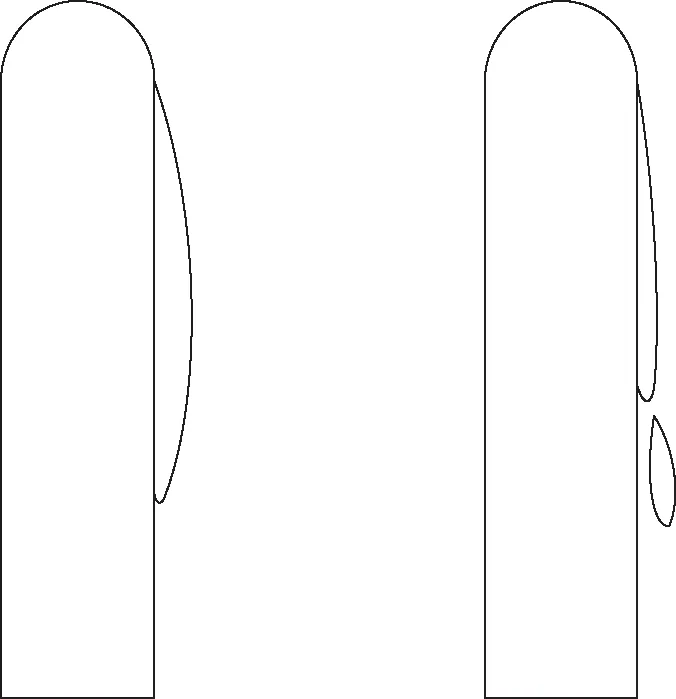
(a)相对稳定的空泡 (b)不稳定空泡图2 稳定与非稳定的局部空泡Fig.2 Stable partial cavity and instable partial cavity
1.3 跨界面运动
水下航行体由水下穿越自由液面进入空气中的“跨界面”运动过程中,由于水的密度是空气密度的800倍,短时间内流场中的介质属性、流动特征等存在突变,特别是存在空泡流动时,还会伴随出水空泡的溃灭,作用在航行体表面的力急剧变化,无论从流场特征随时间和空间的分布,还是航行体表面压力随时间和空间的分布来讲,水下航行体跨界面运动过程受力特征均是一个十分复杂的非线性问题。
1.4 水下流体动力影响因素复杂
航行体水下垂直发射受多因素耦合影响,空泡流体动力更加复杂。如发射水深、平台运动、出筒速度等发射条件及海浪、海流等复杂发射环境均会对水下发射航行体空泡流动产生影响,且各种影响因素之间存在一定的耦合,海浪、海流与平台运动的耦合、发射水深与出筒速度的匹配、尾空泡对附体空泡的耦合影响等众多因素交叉在一起,使得问题的复杂程度和研究难度均较大。
2 水下垂直发射重点关注的几个问题
通过准确把握水下垂直发射过程中航行体受力,确保航行体水下运动弹道稳定及结构完整,对工程研制具有重要意义,水下航行体水下垂直发射需要重点关注以下几个方面的问题。
2.1 附体空泡产生、发展及溃灭
在一定的头型、运动速度和外部环境条件下,当航行体表面的局部压力低于饱和蒸汽压力时,在航行体表面形成附体空泡。随着航行体的运动,空泡形态不断发展演化:一方面,随着航行体运动速度和发射深度的变化,空泡形态不断变化,特别是在有攻角的情况下,迎流面空泡与背流面空泡不对称,空泡形态呈现出较为明显的三维特征;另一方面,由于空泡末端闭合区回射流导致空泡区域和沾湿流区域之间存在一个驻点压力,这个压力为空泡末端的回射压力,水下垂直发射空泡流回射现象见图3。随着空泡长度增加,空泡回射压力向航行体后端移动,形成移动脉冲载荷,见图4。在有攻角的情况下,迎、背水面的回射压力峰值和作用区域不相同,由此使得在空泡末端形成回射压力差,压差在轴向上的作用位置和量值大小随运动过程不断变化,是影响航行体载荷与弹道特性的主要因素之一。
航行体在出水过程中,在大气和空泡内压力的压差作用下,附着水拍击航行体表面形成空泡溃灭,并呈现出逐渐向航行体尾部推进的特征。

图3 水下垂直发射空泡流回射现象Fig.3 Cavity re-entrant jet of underwater vertical launch
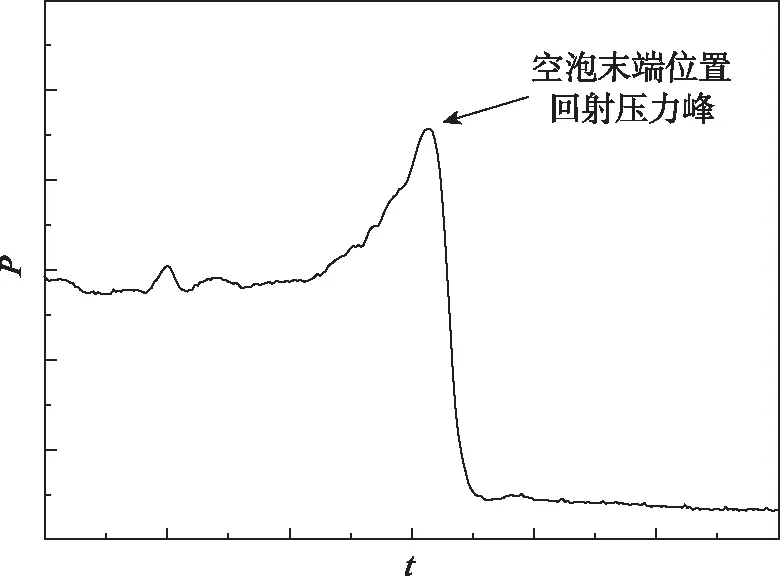
图4 航行体某截面位置处的回射压力Fig.4 Re-entrant jet pressure on the vehicle surface
2.2 尾空泡的非定常发展
不同的尾部形状会使得航行体尾部空泡形成状态具有明显的差异。若航行体尾部为凹面,则有利于弹射燃气跟随航行体运动并形成体积较大的尾空泡,泡内压力基本维持在尾部位置处的静压附近;若航行体尾部为凸面,则不利于弹射燃气的跟随,且受到来流冲刷的作用尾空泡内的燃气量不断减小,泡内压力要低于尾部位置处的静压,呈现负压状态,会导致航行体所受阻力增大。
随着航行体不断运动,尾空泡形态受到发射水深、出筒速度、发射筒口压力分布特征等因素的影响,且伴随着复杂的膨胀、收缩、脱落过程。尾空泡压力是航行体轴向运动速度设计的重要输入,其周期性变化过程对航行体运动特征具有明显的影响。同时,尾空泡内压力的振荡过程也会对附体空泡产生影响。
航行体尾部出水后尾空泡溃灭,产生向上射流冲击航行体尾部形成高压,出现航行体出水尾涌效应,是分析尾部出水过程受力特征需要重点考虑的因素。
2.3 复杂海洋环境影响
航行体水下垂直发射时,海流和波浪等对水质点的扰动形成相对速度,进而对航行体形成附加攻角,速度的切变使得空泡壁面附近的速度沿水深方向产生差异,对空泡形态产生影响,外界干扰的存在会影响和加剧空泡界面的不稳定程度,从而使得流场特征发生变化。
波浪对航行体的影响主要体现在近水面和出水过程中。波高、相位及浪向对航行体位置处静压及攻角均存在明显影响,从而使得空泡推进规律、不对称性存在一定的差异。由于波浪引起的水质点速度随水深分布特性,以及波浪相位点的时变性,使得分析研究波浪对航行体影响的过程具有一定难度和复杂性。
海流表现为不同水深处垂直于航行体轴线的平面内海水流动,可分解为法向海流和横向海流。均匀海流条件下,航行体在水下运动时的攻角发生变化,会造成空泡的不对称性发生变化,进而影响水下运动和载荷特性。当存在流切变时,空泡附近的局部流场也会发生变化。
2.4 运动及载荷特性预示
基于对航行体运动时空泡流特征的认识,掌握影响水下运动参数和载荷的主要因素,建立与之适应的水下运动参数及水载荷预示方法,实现对航行体非定常流体动力、运动参数、载荷的准确预示,为航行体运动稳定性、结构可靠性设计提供依据。在工程实践中,可以通过优化设计,改变空泡流动参数,达到改善流体动力特性的目的,满足航行体运动参数与载荷设计要求。
2.5 小结
水下垂直发射过程中,在航行体表面伴随着复杂的流动现象,其中在航行体表面形成的空泡流改变了航行体表面压力的时间和空间分布特征,直接决定了水下垂直发射过程中的运动和载荷响应,是水下垂直发射航行体最为重要的物理现象,成为水下垂直发射研究的重点和关键。
3 解决水下垂直发射空泡流问题的技术途径
航行体水下垂直发射过程中具有跨介质、非定常、多影响因素的特点,研究难度极大。特别是空泡流的存在,使得航行体表面的受力特征更加复杂,空泡的稳定性、均匀性对水下垂直发射过程具有重要影响,实现对空泡流的调节与控制是解决水下垂直发射问题的核心,目前解决空泡流问题的主要技术途径有以下3个方面。
3.1 水下航行体头型优化技术
头型优化技术是指利用不同头型下的流体动力特点,对水下垂直发射航行体头型进行优化选择,以实现较好的航行体抗空化性能、运动性能的技术。目前水下垂直发射航行体的头型主要可以分为3类,见图5。1)锥型头型,通过选取合适的头锥角,可以获得较好的水下运动特性,航行体稳定性较好;但航行体高速运动状态下往往伴随附体空泡,流体动力相对复杂。2)尖拱型头型,这种头型具有良好的抗空化的能力,水下运动过程中避免自然空泡现象的发生;但由于水的密度远大于空气,此种头型下航行体易出现大姿态变化,运动稳定性差。3)综合锥型和尖拱型优点的流线型头型,这种头型往往需要经过严格的头型优化,以获得良好的抗空化性能和运动稳定性。

(a)锥型 (b)尖拱型 (c)流线型图5 不同的水下航行体头型方案Fig.5 Different headform of the underwater vehicle
3.2 水下垂直发射通气技术
通气技术是通过布置在航行体表面的通气装置向其表面通气以改变其表面流体动力分布特性、优化水下环境的技术手段。通气技术主要有主动空泡技术和被动通气技术。其中主动空泡技术是指利用产气火箭,向已有的航行体肩部空泡内通气的方法,改变空泡内压力,提升空泡的稳定性,优化流体动力特征。被动通气技术是指航行体级间段等腔内携带的气体在腔体内外压差的驱动力作用下,由布置在航行体表面的缝隙结构向航行体外排气,在航行体表面形成气泡以改善航行体水下环境的通气技术。
3.3 水下垂直发射主动控制技术
航行体水下垂直发射过程中,受到发射平台牵连运动、复杂海洋环境的影响,空泡流不稳定发展,流动结构不对称,对水下流体动力产生较大影响。通过采用水下发射主动控制技术增强航行体姿态稳定性,减小外部扰动对空泡稳定性的影响。目前水下垂直发射主动控制技术主要有水下点火技术和栅格翼技术。
水下点火技术是一种依靠发动机推力矢量提高航行体水下发射稳定性的技术方案,能够实现航行体发射平台在大水深、变深度、变航速以及全天候条件下发射。水下点火技术主要利用出口气流改变流向来提供控制力,也称为推力矢量控制技术[5]。
栅格翼是由一组薄的栅格壁镶嵌在边框内组成的蜂窝式结构多面翼,与传统平板翼相比,具有结构轻、升力特性好、铰链力矩小、控制效率高的优点,且栅格翼弦向尺寸小,便于在水下航行体表面紧贴主体折叠安装。栅格翼技术主要通过改变航行体的流体动力特性实现稳定控制,也称为流体动力控制技术。
4 水下垂直发射航行体空泡流研究方法
针对航行体水下发射复杂空泡流动问题,国内外研究人员长期以来开展了理论分析、数值计算和试验研究,取得了一系列的研究成果。
4.1 空泡流势流理论
从18世纪起,基于Helmholtz 和Kirchhoff 提出的自由流线理论(Free Stream-line Theory)和速度图法(Hodograph Method),开启了空泡理论研究的进程。势流理论立足于在无黏流动的范围内解决空泡流问题,把主要精力集中在解决物体附近以及近尾流区外侧的流动,而把复杂的尾流用模型来代替,主要有Riabouchinsky影像模型[6]、开式模型[7]、回射流模型[8]。其共同的假设为空泡内部为等压区,空泡面为自由流线,均未涉及空泡内部流动,空泡尾流闭合的轮廓线示意图见图6,A点即为空泡闭合点。

图6 空泡尾流闭合的轮廓线Fig.6 Outline of the cavitation wake flow closure
Rayleigh在1917年提出了单个球形空泡的动力学方程,为单个空泡发展演化研究提供了途径[9]。自建立可压缩流中球形空泡的运动方程以来,许多学者不断完善和发展空泡溃灭理论。对于偏离球形形状不大的气泡,Benjamin等对空泡壁面作球面函数展开,获得了不可压缩理想流体条件下的近似方程,对非球形空泡溃灭过程也分别开展了理论研究和数值计算[10-14]。在带空泡航行体出水空泡溃灭研究方面,相关学者将三维附体空泡简化为二维圆形空泡的独立溃灭过程,按照球形气泡运动的分析方法建立了空泡溃灭运动的数学模型,通过获取有限厚度水层冲击航行体表面的速度进而获得空泡溃灭的压力。
20世纪50年代,Logvinovich基于势流理论和能量守恒定律提出的空泡截面独立膨胀原理,对轴对称空泡的研究具有十分重要的意义。在理想流体框架内,空泡截面独立膨胀原理认为空泡的每一个横截面按照同一个规律几乎独立于航行体的运动而膨胀收缩,这种规律仅与流场与空泡内部压力之差、航行体运动速度、航行体外形及阻力有关,空泡截面独立膨胀原理示意图见图7。空化器S0为带锐缘的盘形回转体,它的轴线坐标为h,平面Σ垂直于轴线坐标h,t0、t1、t2、t3分别为航行体不同的运动时刻,轴对称空泡起始于空化器锐缘处并逐渐发展。
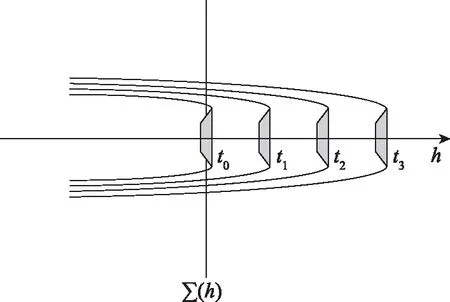
图7 空泡截面独立膨胀原理示意图Fig.7 Schematic diagram of the principle of logvinovish of the cavity sections expansion
空泡流的理论研究基于势流理论、Rayleigh球形空泡运动方程以及独立膨胀原理,这些方法忽略了黏性的影响,对空泡初生、发展、脱落、溃灭等非定常发展过程模拟上缺乏有效的手段,同时对于一些简单空泡流动问题虽然可以获得解析结果,但面临复杂问题时求解难度很大[15]。
4.2 空泡流数值计算
随着计算机技术和计算流体力学的发展,流场数值模拟在空泡流中广泛应用,数值计算得到的水下垂直发射航行体空泡流场图见图8。与通常的流体流动类似,垂直发射航行体流体动力流数值模拟的关键在于准确确定相界面的位置和运动过程,确定各时刻流场区域内各空间位置的物性参数以及发展一套稳健的数值仿真方法。当前关于水下垂直发射流体动力数值仿真研究主要集中在数学模型研究和数值仿真方法研究等。在数学模型方面,通过对不同多相流模型、湍流模型及空化模型下航行体空泡流的数值模拟,研究适用的多相流模型、湍流模型和空化模型;在数值仿真方法方面,主要研究复杂边界下的网格策略、数值求解方法等方面。经过近些年的发展,数值仿真在航行体水下垂直发射多相流研究中的应用越来越广泛。

(a)T1 (b)T2 (c)T3图8 数值计算获得的典型时刻流场图Fig.8 Typical map of the flow field by CFD
4.2.1 数学模型
根据对待流场中不同相的处理方式,数学模型通常可以分为多流体模型和单流体模型[16]。在多流体模型中,认为每一相同时存在于流场中的每一点,各相均独立地满足一组微分方程,通过定义空隙率表征每一相所占的比例。各相的流动参数在界面上发生间断,相界面上存在相的质量、动量和能量传递。多流体模型的控制方程组最为复杂,可以用来分析流场的局部特征。Markatos应用这种方法进行了空泡模拟[17]。由于控制方程复杂,计算量大,当前多流体模型应用并不广泛。单流体模型又称为均相模型或无滑移模型,将计算区域内的多相介质看成是均匀混合的单一介质,物性参数取各相介质对应参数的某种加权平均,采用单相流的研究思路来处理水下垂直发射多相流动问题。
4.2.2 数值计算方法
根据水下垂直发射多相流研究中界面处理思路的不同,研究方法可分为基于空泡面的界面追踪法和基于全流场的界面捕捉法[16]。界面捕捉方法主要包括MAC(Marker And Cell, 标记和单元)方法、Level Set(水平集)模型和VOF(Volume Of Fluid,流体体积法)模型。在界面追踪法中,认为两相之间互不掺混,具有明确的分界面。由于相界面的形状和位置事先未定,因此必须通过界面的运动学或动力学条件,用迭代方法(定常问题)或时间步进方法(非定常问题)确定;界面捕捉法基于全流场Euler方程或N-S方程,通过流场区域中的相分布确定界面位置,是当前多相流研究应用最广泛的方法。国外有关学者采用VOF方法对航行体的水下运动及出水过程进行了数值模拟,获得了自由面变化、空泡流动结构,计算结果与试验结果定性符合[18-19]。
4.3 水下垂直发射试验技术
试验研究是认识水下垂直发射流动物理现象、获得流场特征的重要手段。针对水下垂直发射空泡流与跨界面运动过程中的重要物理现象,水下垂直发射试验技术主要包括空泡流机理试验和跨界面机理研究试验两个方面。
4.3.1 绕航行体空泡流机理试验
空泡流问题作为水下垂直发射的重要物理现象,国内外学者在空泡流机理试验方面开展了大量的研究。Oba等借助LDV(Laser-Doppler Velocimetry,激光多普勒测速)和高速摄像观察了绕圆柱产生的超空泡流情况,尤其仔细分析了脱体点附近的超空化现象[20]。上海交通大学谢正桐、何友声等开展了小攻角下轴对称细长体的通气附体空泡试验,并将测量结果与仿真结果进行了比较[21]。中国船舶科学研究中心易淑群等研究了锥柱组合体模型在轴向约束加速运动中,通气量对加速过程中超空泡形态的影响及变化规律[22],北京理工大学黄彪等利用水平水洞对绕平头回转体的空泡初生开展了实验研究[23]。以上研究大多基于水平水洞开展小尺度试验,见图9所示。在一定流速和压力条件下,测量获得不同攻角、通气参数下的航行体模型受力、航行体表面压力等水动力相关参数,观测通气空泡流动形态的试验。试验的主要目的是了解水下垂直发射多相流动机理,增加对多相流动的感性认识,因此通常缩比尺度较小,在1∶40~1∶80之间,可采用连续通气获得稳定状态下的流场信息。
20世纪50年代,美国加州理工学院等开展了水下轴对称航行体空泡形态和空泡水动力试验研究,并建立了经验预报公式[24]。美国弗吉尼亚理工学院开展了水下高速运动航行体形成的空泡流场的高速PIV(Particle Image Velocimetry, 粒子图像测速)测量研究[25],测量主要集中在航行体模型的出筒过程及其水下运动过程。通过试验,获得了出筒和水下带空泡运动过程中航行体周围速度场的变化、空泡涡环的演变、流场涡量的变化等。在水下航行体研制过程中,美国建立了水下发射平台、高速水槽、高速水洞、高压模拟舱等研究设施,进行了大量的试验研究,涵盖了从缩比模型到全尺寸航行体模型的各种尺度模型。

图9 水平水洞示意图Fig.9 Sletch diagram of cavitation tunnel
4.3.2 航行体跨界面试验
在航行体跨界面机理研究方面,苏联在1960年就建造了大型弹道水池,使用水下拖车和气动弹射器进行出水水动力试验研究。于莫斯科大学、马科耶夫航行体设计局建设大型水洞和弹射水池等试验设施,在水下航行体研制过程中进行了大量的水洞试验和弹射试验。
法国针对出筒过程航行体尾空泡发展进行了大量的模型试验研究,研究内容包括发射气体参数对尾空泡收缩时间和空泡拉断产生的回射流强度的影响等。同时,通过激光片光源结合示踪粒子得到了尾空泡收缩断裂时产生的回射流图片。在水下航行体研制过程中,法国建设了一系列综合试验设施,包括用于弹射试验的水下试验平台、地面发射台和圆形水池等。
国内哈尔滨工程大学、北京理工大学和中科院力学所等均建设了机理研究的弹射试验水槽,对航行体跨界面运动过程中的流场结构进行观测,获得了航行体水下及出水运动过程中的流场结构演化过程和航行体水下运动参数。
5 未来发展趋势
如上文所述,水下垂直发射航行体空泡流是水下航行体研制的核心和关键技术,对未来水下航行体总体性能指标的提升至关重要,其主要的发展趋势主要体现在以下3个方面。
5.1 自由面大变形影响下空泡流数值计算方法
与一般多相流不同的是,水下垂直发射过程受跨波浪自由面运动过程的影响,出水过程中空泡的溃灭过程伴随着大量的飞溅、卷曲等流动现象,局部流动结构复杂,对水下航行体流体动力影响较大。针对波浪自由面影响,需要针对跨界面空泡多相流动过程中多相介质相互作用的特点,发展适用于自由液面大变形状态下的多相流模型,目前比较流行的主要有光滑粒子流体动力学(Smoothed Particle Hydrodynamics, SPH)方法和格子Boltzmann方法(Lattice Boltzmann Method, LBM)。
SPH方法在计算空间导数时不需要使用网格,从而避免了高维拉氏差分网格法中的网格缠结和扭曲,在处理冲击和大变形问题方面具有优越性。该方法能够模拟液滴与液面碰撞、破碎、融合等水流现象,也能表现出水流飞溅、卷曲等复杂的自由表面特征。
LBM基于统计物理学,具有独特的粒子特性,其微观动力学背景使得它具有许多其他基于N-S方程的数值方法所没有的独特优点,LBM方法更能够有效处理大量细小、分散截面的飞溅流动问题、高速入水问题等。
5.2 复杂环境的适应能力研究
海浪是海水运动的重要形式之一,自由面波浪作用下海水的质点运动对水下航行体水中和出水运动过程空泡流均有较大影响。近年来,随着对水下垂直发射航行体性能的要求不断提高,水下垂直发射航行体空泡流对复杂海洋环境的适应能力受到越来越多的关注。然而自然界中存在的海浪变化特性十分复杂,海浪呈现出不规则的特征,海洋环境对空泡发展的影响研究难度较大。
计算机技术和数值计算方法的飞速发展为水下垂直发射航行体空泡流复杂环境适应能力研究提供了技术手段。目前对数值仿真中波浪的处理作为理想的规则波模型,对随机海浪谱特性下航行体数值仿真计算尚未涉及,难以考虑波浪随机性对空泡流发展的影响,后续应结合高精度的数值计算模型和波浪谱方法,建立波浪要素对航行体流体动力特征的理论预示模型,形成随机海浪谱下航行体空泡多相流数值仿真计算方法。
5.3 考虑空泡影响的流固耦合研究
对垂直发射水下航行体而言,在水下航行阶段和穿越水面的过程中,空泡流水动力的作用使航行体产生弹性振动,影响周围流场的变化,致使航行体结构物的附加质量、阻尼特性发生变化,空泡形态及其溃灭特性也随之发生变化,从而形成航行体水下运动的流固耦合问题。
当前对流固耦合问题的研究主要有数学解析、实验分析和数值计算3种方法。其中数学解析方法要将含有流固互动的对象用统一的数学模型来描写,求解十分困难;实验分析方法成本较大,实验条件要求很高,某些极端情况可能用实验较难实现;目前最常用的是数值计算方法,主要采用CFD(Computational Fluid Dynamics,计算流体动力学)与CSD(Computational Structural Dynamics,计算结构动力学)的方法,具有成本低、开发周期短的特点,通过更改参数设置,就可以对多种工况进行研究,是实验分析方法强有力的补充和支撑。
6 结语
水下垂直发射航行体空泡流研究是水下航行体研制的核心与关键,由于水下垂直发射跨界面、跨介质的运动过程,空泡多相流体动力具有非定常、非线性的特征,影响因素复杂。通过采用头型优化技术、水下垂直发射通气技术和水下主动控制技术实现对空泡流的调节与控制,基于势流理论、数值仿真和试验模拟开展空泡多相流研究,揭示水下垂直发射空泡多相流动机理,为解决水下垂直发射空泡流作用下的结构响应和运动姿态问题奠定基础。针对水下垂直发射空泡的技术难点,未来应从自由面大变形影响下空泡多相流数值仿真方法、复杂海洋环境适应能力研究和流固耦合技术等方面开展空泡多相流的机理性、基础性和探索性研究,以更好地提升水下航行体总体性能,创新研发新型水下发射技术方案,牵引水下发射相关基础学科发展。
[1] Brennen C E. Cavitation and bubble dynamics[M]. Oxford University Press,1995.
[2] Franc J P. Partial cavity instabilities and re-entrant jet[C]. Proceedings of the 4thInternational Symposium on Cavitation, California, USA: Lecture 002,2001.
[3] Franc J P, Michel J M. Fundamentals of cavitation[M]. Springer Science & Business Media, 2006.
[4] 刘桦, 刘庆华, 胡天群. 带空泡轴对称细长体水动力脉动的实验研究[J]. 水动力学研究与进展: A 辑, 2004, 19(6): 794-800.
[5] 蔡廷湘. 水下点火与水下发射[J]. 舰载武器, 1999 (4): 7-12.
[6] Riabouchhinsky D. On steady flow motions with free surfaces[J]. Proceedings of the London Mathematical Society, 1920, 19: 206-215.
[7] Wu T Y T. A wake model for free-streamline flow theory part 1:fully and partially developed wake flows past an oblique flat plate[J]. Journal of Fluid Mechanics, 1962, 13(2): 161-181.
[8] Kreisel G. Cavitation with finite cavitation number[M]. Admirally Res. Lab. Rep.,R1/H/36,1946.
[9] Rayleigh L. On the pressure developed in a liquid during the collapse of a spherical cavity[J]. Philosophical Magazine Series,1917, 34: 94-98.
[10] Benjamin T B, Ellis A T. The collapse of cavitation bubbles and the pressures thereby produced against solid boundaries[J]. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 1966, 260(1110): 221-240.
[11] Shima A. The behavior of a spherical bubble in the vicinity of a solid wall[J]. Journal of Basic Engineering, 1968, 90(1): 75-89.
[12] Mitchell T M, Hammitt F G. Asymmetric cavitation bubble collapse[J]. Journal of Fluids Engineering, 1973, 95(1): 29-37.
[13] Hsieh D Y. Varitational method and dynamics of nonspherical bubbles and liquid drops[C]. Finit-Amplitude Wave Effects in Fluids, Proceedings of the 1973 symposium, Copenhagen, 1974.
[14] Bevir M K, Fielding P J. Numerical solution of incompressible bubble collapse with jetting in moving boundary problems in heat flow and diffusion[M]. Clarendon Press, 1974.
[15] 陈鑫. 通气空泡流研究[D]. 上海: 上海交通大学, 2006.
[16] 车得福, 李会雄. 多相流及其应用[M]. 西安: 西安交通大学出版社, 2007.
[17] Markatos N C. Modelling of two-phase transient flow and combustion of granular propellants[J]. International Journal of Multiphase Flow, 1986, 12(6): 913-933.
[18] Meier M, Yadigaroglu G, Smith B L. A novel technique for including surface tension in PLIC-VOF methods[J].European Journal of Mechanics-B/Fluids, 2002, 21(1): 61-73.
[19] Hirt C W, Nichols B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J].Journal of Computational Physics, 1981, 39(1): 201-225.
[20] Oba R, Ikohagi T, Yasu S. Supercavitating cavity observations by means of laser velocimeter[J]. Journal of Fluids Engineering, 1980, 102(4): 433-438.
[21] 谢正桐, 何友声. 小攻角下轴对称细长体的充气肩空泡试验研究[J].实验力学, 1999, 14(3): 279-287.
[22] 易淑群, 惠昌年, 周建伟, 等. 通气量对轴向加速过程超空泡发展规律影响的试验研究[J]. 船舶力学, 2009(4): 522-526.
[23] 黄彪, 王国玉, 权晓波, 等. 绕平头回转体非定常空化流体动力特性研究[J]. 实验流体力学, 2011, 25(2): 22-28.
[24] Kiceniuk T. An experimental study of the hydrodynamic forces acting on a family of cavity-producing conical bodies of revolution inclined to the flow[R].Hysrodynamics Laboratory California Institute of Technology, Pasadena, California, 1954.
[25] 申功炘, 张永刚, 曹晓光, 等. 数字全息粒子图像测速技术(DHPIV) 研究进展[J].力学进展, 2007, 37(4): 563-574.

