超声磨削表面三维形貌建模与试验研究

李 虎，陆忠东,2

(1.上海理工大学 机械工程学院，上海 200093；2.上海电机学院，上海 201306)

随着机械、电子、信息、能源、航空航天、国防等领域高端装备的不断发展，出现了一大批性能要求越来越高的零部件[1]。这些零部件对硬脆性材料、难加工材料和新型先进材料的需求日益增多，对关键零件的加工效率、加工质量和加工精度提出了更高的要求。传统加工方法是超精密磨削和单点金刚石切削，产生较大的磨削力以及磨削热，引起工件表面、亚表面损伤以及砂轮寿命低；严重制约着零件加工精度及加工效率，迫切需要新的磨削工艺来解决此类问题。最近发展起来的超声磨削就是解决此类问题的方法之一。

超声磨削加工是在传统磨削过程中对砂轮或工件施加超声振动，改变磨粒和工件的干涉过程，从而获得更好的加工效果。文献[1]对改性氧化铝陶瓷进行超声磨削形貌研究，结果表明加工表面上可以观测到晶粒细化现象,几乎没有破碎发生,材料去除模式主要为塑性去除。文献[2～10]研究了不同砂轮粒度、各磨削用量对超声磨削的粗糙度和磨削力的影响规律。文献[11]研制了一种新型的超声磨削装置，并且实验证明该装置超声磨削单晶硅时磨削力下降20%，表面粗糙度下降30%。

本文利用分析了超声磨削磨粒运动轨迹和磨削表面形貌形成机理，建立了超声磨削三维形貌模型。通过进行超声振动辅助磨削实验，验证了超声辅助磨削表面三维形貌模型的正确性。

1 砂轮表面三维形貌建模

砂轮制造过程中，粒度号和组织号是其主要的特征参数，分别表示了磨粒的大小和分布浓度。马尔金[12]通过对不同型号砂轮进行了统计分析，给出了磨粒平均直径dav、砂轮浓度Vg与粒度号和组织号之间关系式

dav=68M-1.4

(1)

Vg=2(32-S)/100

(2)

式中，M为砂轮粒度号；S为组织号。

由磨粒平均直径dav和砂轮磨粒浓度Vg可计算出磨粒平均间隔距离lr关系为[13]

(3)

初始条件时，磨粒按照间隔lr均匀放置，随后根据正态分布随机改变每个磨粒直径，并对磨料的坐标进行随机移动。为防止磨粒之间干涉，需使任意两个磨粒之间的距离大于其半径之和，否则重新赋予随机移动量，公式为

(4)

式中，xkn、ykn和zkn分别为第K个磨粒第N次移动后坐标。xk0、yk0和zk0为第N-1次移动后坐标。δx、δy和δz为x、y和z方向随机移动量δx、δy、δz∈(-lr,lr)。

为了提高磨粒的随机分布程度，需要对齐进行多次随机移动，经过随机移动后得到直径服从正态分布，空间位置随机分布的磨粒，其表层磨粒能表征砂轮的表面形貌[14]。为提取表层磨粒，假定磨粒随机移动前，表层磨粒的中心平面为零基准平面，随机移动后与零基准平面干涉的磨粒即为表层磨粒，得到砂轮表面形貌如图1所示。

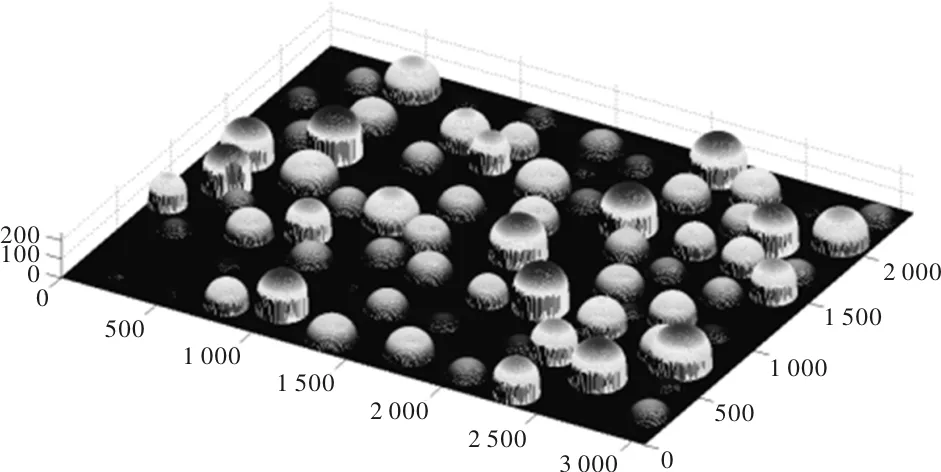
图1 WA60K10V砂轮表面形貌

砂轮表面形貌通常用拓扑矩阵表示，即将砂轮表面离散为点集，拓扑矩阵中元素位置表征离散点在砂轮圆周面上位置，即图1中的x、y坐标值；元素值表征离散点的高度值，即图1中的z坐标值。为砂轮表面形貌离散点间距，将mesh L基准平面和表层磨粒表面以Lmesh大小离散为点集，可生成砂轮表面形貌拓扑矩阵G0(m,n)。其中m，n为离散点坐标x、y值相关，z值为矩阵元素值。为方便磨削过程中磨粒运动轨迹的分析，需将砂轮表面离散点高度值加上砂轮半径作为描述砂轮表面初始形貌拓扑矩阵Gint(m,n)的元素值，如式(5)所示。

Gint(m,n)=G0(m,n)+rs

(5)

式中，rs为砂轮的基准半径。

2 超声振动辅助磨削表面三维形貌模型

2.1 超声振动辅助磨削磨粒运动模型

工件表面形貌是磨粒在工件上划擦、耕犁和切除的综合作用的结果。在仿真模型中需对问题进行简化，即假设磨粒与工件干涉时，都去除材料。本文研究的超声振动为加载在工件上的轴向振动，设某一磨粒位于坐标原点，初始时刻t0为零，超声振动相位角为零，则在t1时刻砂轮上该磨粒的运动轨迹可分解为：砂轮旋转的运动、工作台进给运动和超声振动运动，在直角坐标系中磨粒轨迹方程如式(6)所示。

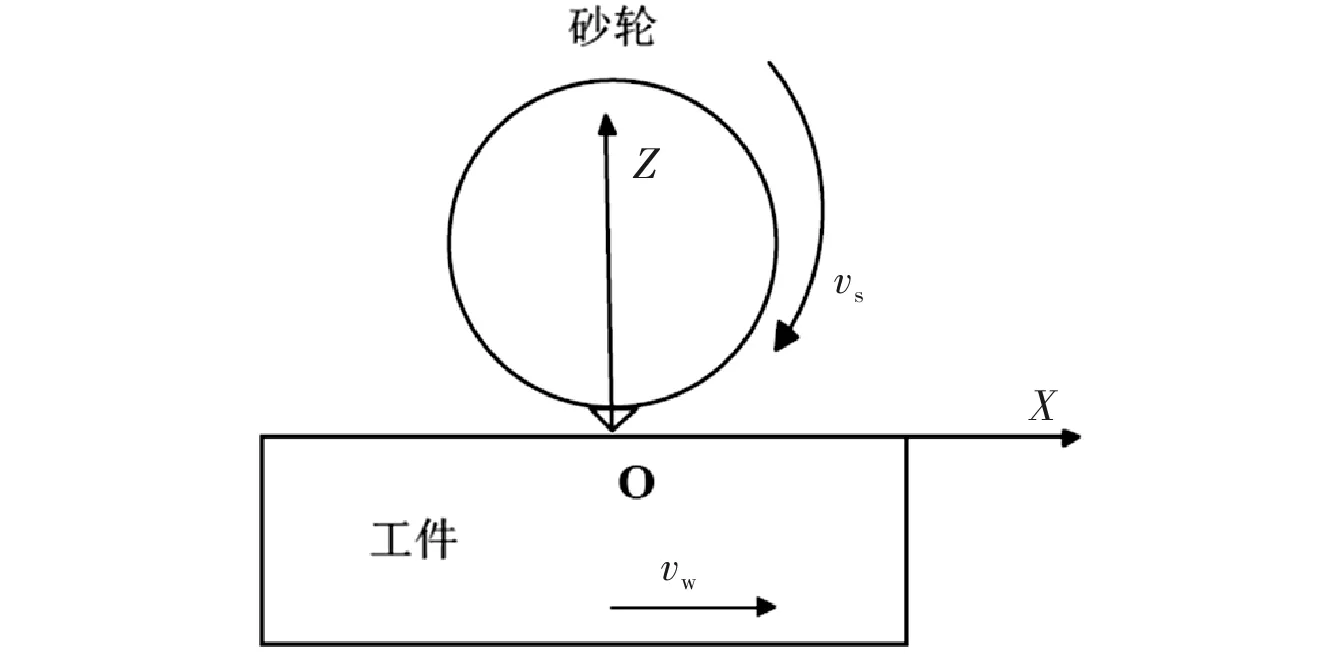
图1 磨粒运动示意图

(6)

式中，vw为工作台速度；rg为该磨粒在Gint相应位置的元素；ws为角速度(ws=vw/rs)；A为超声振动辅助；ω为超声振动频率。

根据磨粒运动轨迹方程，对轴向超声振动辅助磨削磨粒的运动轨迹仿真如图2所示。

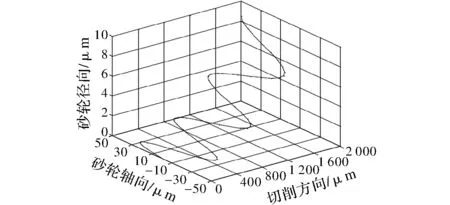
图2 轴向超声振动单颗磨粒运动轨迹

从图2中可以看出，在单颗磨粒切削过程中，在轴向方向进行正弦曲线振动，大量磨粒经过时，从而增加了磨粒与工件的干涉，使工件表面沟槽变宽、峰值降低，实现粗糙度的降低。

2.2 磨粒轨迹离散

工件表面形貌通常也采用拓扑矩阵表示。设坐标系原点建立在磨削前的工件表面上，设此时初始时间为零，超声振动相位为零，磨削方式为逆磨，磨粒a位于坐标系原点，磨粒a的运动轨迹如图3所示。

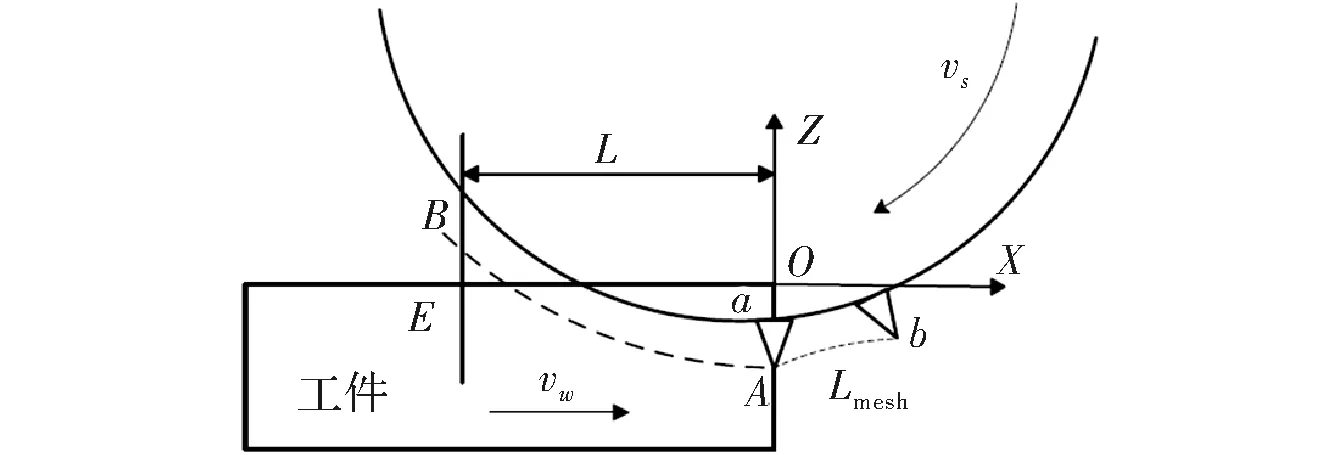
图3 磨粒a运动轨迹

为计算长度为L的OE区间内磨削后表面三维形貌，需计算出经过该区间内所有磨粒的轨迹，可求得磨粒a经过OE之间弧长用时间tL：例如磨粒a接触到工件的轨迹为弧线AB。由式(6)中第一个公式，可知逆磨时磨粒a经过OE之间弧长所用时间tLa与L之间关系为

L=-vwtLa-rgsim(wstLa)

(7)

将tL均分200份为tLn，得到磨粒a经过OE范围时每个时间点数值tga，分别依次代入式(6)，即调整坐标系后可求出该磨粒a经过轨迹AB时的x、y和z坐标[15]。

(8)

式中xan,yan,zan为磨粒a运动轨迹离散后的x,y,z坐标，rg为磨粒a在砂轮形貌拓扑矩阵Gint相应位置的元素。rmax为砂轮形貌拓扑矩阵中最大值，下一个磨粒b的轨迹如图4所示。

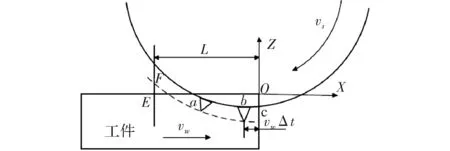
图4 磨粒b运动轨迹

由式(6)可知，不同磨粒经过OE范围内所用时间tL可近似看做相等，即tL=tLa。记tL均分200份为tLn，磨粒a转到磨粒b时间为Δt,当计算b磨粒在x轴上O～E范围之间轨迹时，将轨迹坐标原点平移到磨粒b所在位置。

(10)

xb=-vwtLn-rgbsin(wstLn)-vwΔt

(11)

同时计算磨粒b的时间范围tLn需要磨粒a基础上提前Δtg。

(12)

(13)

因此对于第k个磨粒在X轴上O～E范围之间轨迹离散后坐标可求出

(14)

2.3 最小值包络面求解模型

根据砂轮表面轮廓形貌矩阵Gint和式(14)可计算出各个磨粒的运动轨迹点坐标，取其最小值的包络面就是磨削后工件表面形貌[11]。由于砂轮线速度和工作台速度的速度比很大，需要计算大量的磨粒轨迹及其坐标位置，而且轨迹坐标数据的x和y不均匀分布，不易实现轨迹坐标值之间比较，因此需要一种简便的算法来实现最小值包络面的构建。如图5所示，求出砂轮轴向一列的运动轨迹。在xy平面上划分10 μm×10 μm网格，将曲线投影到xy平面，用3个矩阵Ax，Ay和Az用来储存每次计算的坐标。

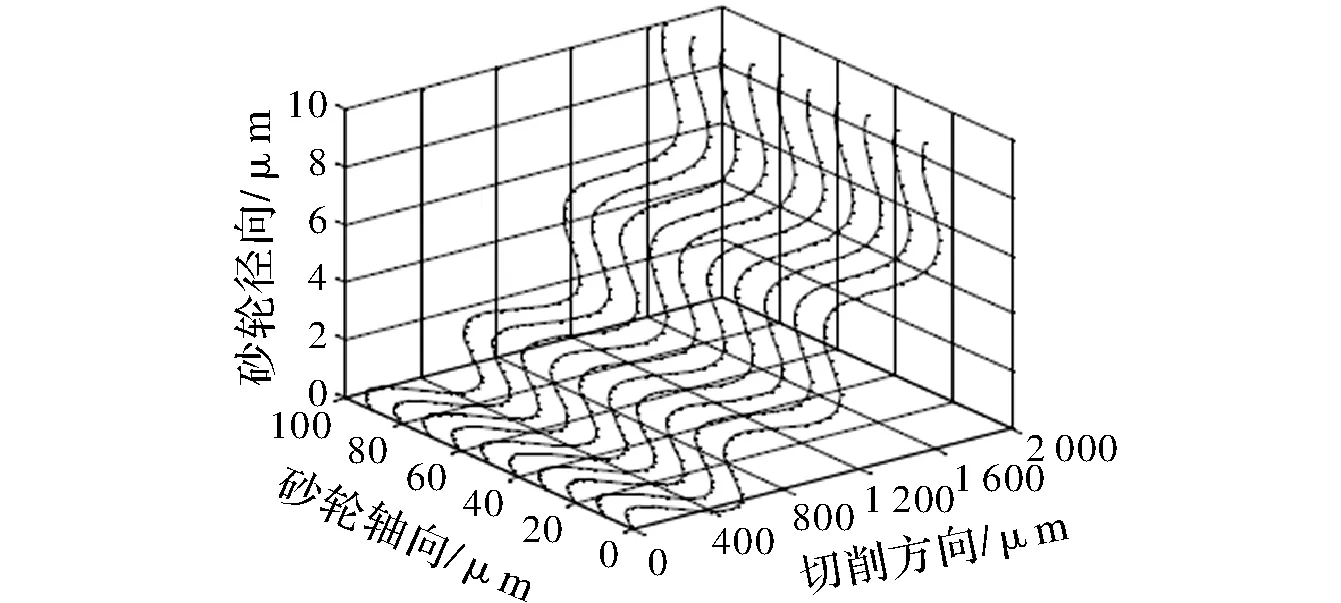
图5 轴向一列磨粒运动轨迹

当砂轮上磨粒k的轨迹上第n点坐标为xkn,ykn和zkn

m=ykn/10
n=xkn/10

(10)

对m,n进行向上取整数后，有

(11)

对砂轮轴向下一列磨粒运动轨迹坐标进行计算，同理赋值到矩阵Ax1,Ay1和Az1中，从而得到另一列磨粒的磨削过后的工件表面轮廓数据[12]。将该相邻的两列磨粒的轨迹矩阵对比，取高度值z较小的元素。最终可得到所有磨粒轨迹的最小值在各自网格内的最小值，通过三角插值算法，就可以得到磨粒运动轨迹的最小值包络面。设超声振幅A为零时，可得到普通磨削时的工件表面形貌。

3 超声辅助磨削试验

3.1 实验设备及条件

为了验证超声辅助表面形貌模型的正确性，在自行设计的超声辅助磨削工作台的上进行了磨削试验。磨削试验在斯来福临K-P48T平面磨床进行，砂轮型号为WA46H10V，砂轮外径220 mm，宽度50 mm。工件材料为轴承钢Gcr15，尺寸长宽高为：80 mm×20 mm×35 mm。磨削方式为逆磨。粗糙度是在Taylor粗糙度仪上测量的，表面形貌是在Taylor白光干涉仪上进行的。

3.2 实验方案

实验分别进行普通磨削和超声振动辅助磨削，以此来验证磨削表面形貌模型真正确性，并研究超声振动辅助磨削对磨削表面形貌的影响与磨削参数之间的关系。

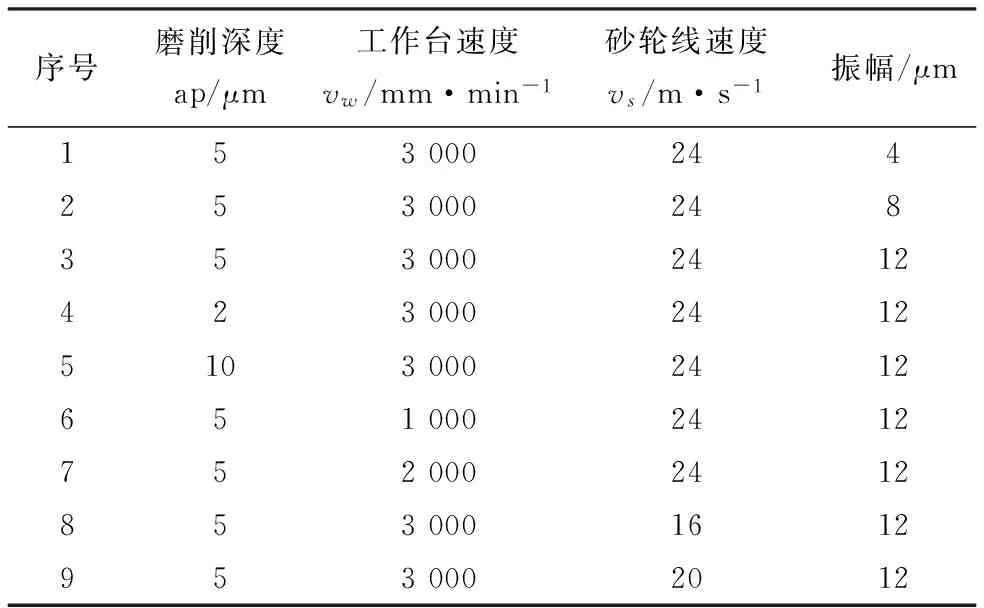
表1 磨削用量

3.3 结果与分析

通过白光干涉仪对相同磨削参数下普通磨削和轴向超声振动辅助磨削的工件表面形貌进行了测量，工件三维形貌对比如图6所示。

图6 普通磨削和超声磨削的工件表面三维形貌

从图6可以看出，普通磨削时工件表面轮廓峰高和轮廓谷深差值较大，而轴向超声振动辅助磨削的工件表面，轮廓峰谷数量增多，峰高和谷深差值减小，表面形貌高度值更加均匀。白光干涉仪对工件表面粒子数进行统计分析表明，普通磨削时表面形貌的突出高度大多集中在3.25 μm附近，而超声振动辅助磨削表面突出高度大多集中在2 μm 附近，由此可以看出超声振动辅助磨削时磨粒的轴向振动增大磨粒与工件的相互干涉切削，使轮廓峰高部分被切削去除，使表面形貌高度值更加均匀。

3.4 表面三维形貌仿真结果分析

为验证超声振动辅助磨削表面三维形貌模型的有效性，利用Matlab编程生成了磨削表面三维形貌，仿真所使用砂轮直径、磨粒参数、磨削深度、工件速度和砂轮线速度都和实际试验参数一致。由于砂轮线速度与工作台速度之比过大，磨削时大量磨粒经过工件表面，要仿真较大面积的磨削表面三维形貌需要大量的计算资源，本文仿真三维形貌大小为1 mm×1.2 mm。在仿真过程中，进行一次磨削，会留下未切除量，影响仿真的准确性，仿真时至少切除两次。表面形貌的散点位置坐标不规则，散乱的分布在三维空间内，需要进行插值来生成表面三维形貌。仿真出的三维形貌图和实测图如图7所示。

图7 普通磨削/超声磨削的仿真与实测图对比

由图7(a)和图7(b)的普通磨削实验和仿真对比可知，仿真模型能反应磨削表面的基本形貌特征，但由于磨粒被简化为规则的球形，导致表面沟槽十分规则，不能精确模拟磨粒随机切削的过程。由图7(c)和图7(d)超声振动辅助磨削时实验测试结果和模型仿真结果对比可知，超声振动辅助表面三维形貌模型能够模拟轴向超声振动去除沟槽峰值的能力，有助于理解轴向超声振动磨削表面形貌生成的机理。

4 结束语

(1)本文分析了轴向超声振动辅助磨削时磨粒与工件的相对运动轨迹，提出了大量随机分布磨粒切削工件路径的离散算法和随机离散点最小高度值包络曲面提取算法，实现了超声振动辅助磨削表面三维形貌模型的建立；(2)通过白光干涉仪对普通磨削和轴向超声振动辅助磨削的工件表面进行了测量，对比两者发现轴向超声振动辅助磨削工件表面沟槽深度明显小于普通磨削工件的表面。同时对轴向超声振动辅助磨削表面三维形貌模型生成的工件形貌和实验测量表面进行对比，验证了超声振动磨削表面三维形貌模型的有效性。

[1] 郭东明,孙玉文,贾振元.高性能精密制造方法及其研究进展[J].机械工程学报,2014,50(11):119-134.

[2] 张洪丽.超声振动辅助磨削技术及机理研究[D]. 济南:山东大学,2007.

[3] 闫艳燕,栗成杰, 赵波,等.二维超声磨削纳米氧化锆陶瓷的磨削力特性研究[J].中国机械工程,2008,14(19):1270-1274.

[4] 吴雁,朱训生,赵波.工件横向施振超声振动磨削力特性实验研究[J].机械科学与技术,2006,25(2):146-148.

[5] 曲云霞,关颉文.超声振动磨削对工件表面粗糙度的影响[J].河北工业大学学报,1997,26(3):99-104.

[6] 吴春兰,韩晓红.3D 打印技术对我国制造业带来的机遇探讨[J].兰州交通大学学报,2014(2):128-130.

[7] 谭德远.黄金树结构两种节点可选方案的性能比较[J].钢结构,2002,17(59):19-20.

[8] 孙光永,李光耀,陈涛,等.多目标粒子群优化算法在薄板冲压成形中的应用[J].机械工程学报,2009,45(5):153-159.

[9] Agarwal S,Venkateswara P.Predictive modeling of force and power based on a new analytical undeformed chip thickness model in ceramic grinding[J].International Journal of Machine Tools & Manufacture,2013,18(65):68-78.

[10] 冯继伦.磨削表面粗糙度及其概率统计问题[J]. 机械设计与制造,1982,34(4):34-38.

[11] Azarhoushang B,Tawakoli T.Development of a novel ultrasonic unit for grinding of ceramic matrix composites[J].The International Journal of Advanced Manufacturing Technology,2011,57(5): 945-955.

[12] 马尔金.磨削技术理论与应用[M].蔡光起,巩亚东,宋贵亮,译.沈阳:东北大学出版社,2002.

[13] Xun Chen,Rowe W Brian.Analysis and simulation of the grinding process,part I:generation of eht grinding wheelsurface[J].International Journal of Machine Tools Manufact,1996,36(8):871-882.

[14] 刘月明,巩亚东,曹振轩.基于数值建模的砂轮形貌仿真与测量[J].机械工程学报,2012,48(23):184-190.

[15] Hou Zhenbing,Komanduri R.On the mechanism of the grinding process-part1 stochastic nature of the grinding process[J].International Journal of Machine Tools & Manufacture,2003,43(15):1579-1593.