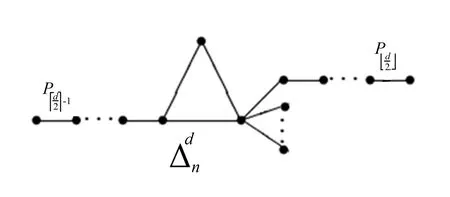
具有固定直径单圈图的Estrada指标

杨迎迎, 常 安

(福州大学数学与计算机科学学院,福建 福州 350116)

0 引言

本研究所讨论的图均为简单图. 设G是一个n阶图,其顶点集为V(G)={v1,v2, …,vn}. 图G的邻接矩阵是一个n阶(0, 1)-矩阵,记为A(G)=(aij). 其中,如果顶点vi和vj相邻,那么aij=1,否则aij=0.G的特征多项式为P(G,λ)=det[λI-A(G)],其中I是n阶单位矩阵.P(G,λ)=0的根即为图G的特征值,记为(λ1(G),λ2(G), …,λn(G)).

1 预备知识

设G、 H是两个点不交的连通图,v1、 v2分别是图G、 H的两个顶点,将v1和v2粘合在一起形成一个新点u,称这一过程为图的粘合[7], 所得的图记为G(v1)∘H(v2)或者H(v2)∘G(v1). 下面是证明本研究主要结论所需要的几个引理.

引理1[4]设G和H是两个点不交的连通图,u, v∈V(G),z∈V(H),并且 |V(H)|≥2. 记G1=G(u)∘H(z),G2=G(v)∘H(z). 如果对任何正整数k都有Mk(G; u, u)≥Mk(G; v, v),并且至少有一个k0满足Mk0(G; u, u)>Mk0(G; v, v),则EE(G1)>EE(G2).

(a) G′ (b) G″图1 引理2中的图G′和G″Fig.1 G′ and G″ in Lemma 2

(a) G1 (b) G2 (c) G3图2 引理3中的G1,G2和G3Fig.2 G1, G2 and G3in Lemma 3

引理2[4]设G1和G2是两个连通图,且u∈V(G1),v∈V(G2). 图G′表示将点u和点v用一条边连接得到的图,图G″表示将点u和点v粘在一起,并且在这个公共点u(v)上增加一条悬挂边得到的图,如图1所示. 如果dG1(u)≥2,dG2(v)≥2,则EE(G″)>EE(G′).

引理3[1]设G、G′、G″是三个点不交的连通图,u,v∈V(G),u′∈V(G′),u″∈V(G″). 图G1、G2、G3是由图G、G′、G″构造出来的图. 其中,G1是分别将点u和点u′,点v和点u″粘在一起得到的图； 图G2是将u、u′、u″三点粘在一起得到的图； 图G3是将v、u′、u″三点粘在一起得到的图,如图2所示. 则EE(G2)>EE(G1)或EE(G3)>EE(G1).更进一步,如果dG(u)≥dG(v),有EE(G2)>EE(G1)； 如果dG(v)≥dG(u),有EE(G3)>EE(G1).

设Cn表示n个顶点的圈.Cn上的顶点按顺时针顺序标为u1,u2, …,un.

引理4[1]设G是一个连通图,并且Cl是图G上圈长为l≥5的圈. 如果在Cl上存在一个度数为2的点(设为ul),并且点ul-2与点u1不相邻,则存在另外一个图G′=G-u1ul+u1ul-2,图G′中有一个圈长为l-2的圈,并且EE(G′)>EE(G).

引理5[7]设图G中有两个顶点u,v,设wi∈V(G),uwi∉E(G),vwi∉E(G)(i=1, 2, …,k). 定义Eu={uwi,i=1, 2, …,k},Ev={vwi,i=1, 2, …,k}.Gu=G+Eu,Gv=G+Ev. 如果(G;u,u)<(G;v,v)并且(G;u,wi)≤(G;v,wi)(i=1, 2, …,k),则有EE(Gu)

2 主要内容

证明 首先证明在图G中,对任意正整数k,都有Mk(G;u,u)≥Mk(G;v,v). 显然M1(G;u,u)=0,M1(G;v,v)=0；M2(G;u,u)≥2,M2(G;v,v)=2；M3(G;u,u)≥0,M3(G;v,v)=0. 当k≥4时,对于∀wk(G;v,v)∈Wk(G;v,v),分两种情况考虑.

图3 从G到H的转换Fig.3 The transformation from G to H

(a) 形式1 (b) 形式2图图类中的两种形式

证明 下面分两种情况讨论.

图5 引理7中图的转换Fig.5 The transformation of graph in lemma 7

图

由引理6～7的结论,即可得到下面主要结果.

[1]BAMDADH,ASHRAFF,GUTMANI.LowerboundsforEstradaindexandLaplacianEstradaindex[J].AppliedMathematicsLetters, 2010, 23(7): 739-742.

[2]FATH-TABARGH,ASHARFIAR.NewupperboundsforEstradaindexofbipartitegraphs[J].LinearAlgebraandItsApplications, 2011, 435(10): 2607-2611.

[3]DUZB,ZHOUB.TheEstradaindexofunicyclicgraphs[J].LinearAlgebraanditsApplications, 2012, 436(9): 3149-3159.

[4]WANGL,FANYZ,WANGY.MaximumEstradaindexofbicyclicgraphs[J].DiscreteAppliedMathematics, 2015, 180(10): 194-199.

[5] 滕海滨. 单圈图的匹配与Estrada指标[D]. 合肥： 安徽大学,2013： 1-30.

[6]CVETKOVICDM,DOOBM,SACHSH.Spectraofgraphstheoryandapplication[M].NewYork:AcademicPress, 1980.

[7]WANGWH,XUWW.GraphswiththemaximalEstradaindices[J].LinearAlgebraanditsApplications, 2014, 446(1): 314-328.