基于四元数互补滤波算法的前臂假肢手部自平衡系统设计

王传江 王栋 侯鹏亮 袁振 张远来

（1山东科技大学机器人研究中心，山东青岛,266590； 2山东省机器人与智能技术重点实验室，山东青岛，266590；3山东大学控制科学与工程学院，济南,250061）

0 引言

目前，市场上大部分前臂假肢多为装饰假肢，仅仅起到美观、装饰的作用，并不能真正实现其代偿功能。为了满足前臂截肢者端水等基本日常生活需要，本文设计了一种两自由度电动前臂假肢手部自平衡系统，通过控制前臂旋转和手腕俯仰，使得患者前臂假肢在运动过程中其假肢末端手部虎口处始终与水平面保持平行。

前臂假肢手部自平衡系统主要包括姿态解算和手臂控制两部分，由于人类在运动时所做动作的复杂性和不确定性，因此要使假肢手部能够在运动时始终保持平衡，姿态解算则是实现该系统自平衡的关键问题之一。

姿态解算的速度和精度会直接影响整个系统的稳定性和可靠性，是实现手臂控制的重要前提和基础。姿态解算需要依靠惯性测量器件，而MEMS器件由于具有小体积、低成本、低功耗等特点，因此成为前臂假肢惯性测量器件的首选。但是，由于MEMS器件容易受温度和外界噪声的影响，需根据姿态解算算法对其进行多传感器的数据融合，才能得到实时准确的姿态。

目前，常用的多传感器姿态解算算法有基于四元数的卡尔曼滤波[1]、基于四元数的扩展卡尔曼滤波[2]、欧拉角法等。其中，卡尔曼滤波所需计算量较大，在低频处理器上运行，其输出姿态的实时性和可靠性较低；而欧拉角法则存在万向节死锁的问题。

针对上述问题，本文采用了互补滤波算法对前臂假肢手部进行姿态估计，实验表明，该算法通过对加速度计和陀螺仪进行互补融合，有效地消除了漂移误差，能够快速、可靠地跟踪手部姿态，并且实现前臂假肢手部的自平衡。

1 硬件系统设计

本文设计的前臂假肢除了能够实现手部自平衡，还可实现手部的张合、内外转动等动作，为了使假肢使用者能够更加简单、有效地对其进行操控，该前臂假肢采用LD3320语音识别模块来接收使用者的控制指令。LD3320语音识别精度高、功耗低，可对多条关键词进行识别，能够满足该前臂假肢设计需要。

惯性测量单元采用MPU6050传感器，其集成了3轴加速度计和3轴陀螺仪，免除了组合加速度计与陀螺仪时间轴之差的问题。前臂假肢硬件系统结构示意图如图1所示。

图1 前臂假肢硬件结构

在该系统中，MPU6050传感器安装在前臂旋转电机固定支架上，前臂假肢机械结构示意图如图2所示。初始条件下，MPU6050传感器应与手部虎口处保持平行。当主控芯片STM32接收到语音识别单元的“自平衡”指令后，前臂假肢进入自平衡模式，此时STM32通过采集MPU6050的原始数据进行姿态解算，然后根据解算姿态计算出舵机所需控制角度，并通过RS485通信把控制量发送给舵机，从而使手部虎口处始终与水平面保持水平。

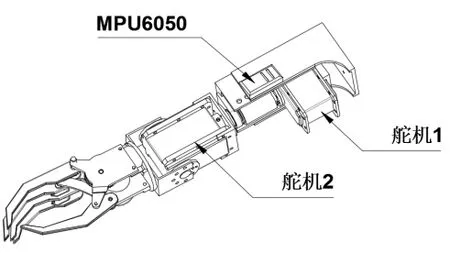
图2 前臂假肢机械结构

2 互补滤波姿态估计算法

2.1 坐标系描述

为了描述前臂假肢手部的姿态信息，本文定义了2个不同的空间三维坐标系，分别为参考坐标系 和载体坐标系 ，如图3所示。

图3 参考坐标系与载体坐标系的关系

2.2 坐标系间的转换关系

式（1）中， 为坐标转换矩阵，也称为姿态矩阵[3-4]，欧拉角所表征的 表达式为：

式（2）中所表示的姿态矩阵，由于计算量大，在微控制器中运行效率低，无法满足姿态的实时性要求，所以本文采用四元数法进行姿态解算。四元数定义为 ：

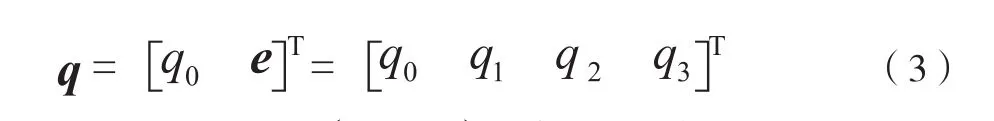
式（3）中， ，其为四元数 的矢量部分；为四元数 的标量部分。由四元数运算法则可知，四元数 满足的归一化约束条件为：

则坐标系 和 之间四元数转换矩阵为[5]：

由式（2）和式（4）可得载体姿态角为：

2.3 四元数姿态更新算法

由四元数性质可知，四元数的更新本质就是求解四元数微分方程，四元数微分方程表示为[6]：

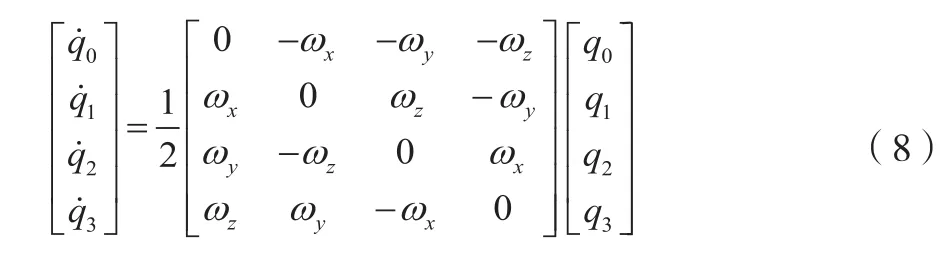
假设系统采样周期为T，在(t，t+T)时间间隔内，角速度 、 、 为三轴陀螺仪的输出，采用一阶龙格库塔法求解四元数微分方程为：

根据公式（9）和公式（10），可得t+T时刻的四元数(t+T)，将(t+T)代入公式（6）可得t+T时刻的三轴欧拉角

2.4 互补滤波姿态融合

综上可知，姿态更新算法主要是对陀螺仪数据进行迭代运算。虽然陀螺仪的动态性能好，短时间内数据精度高，但随着时间的延长，其容易受外界环境、温度等影响而产生随机漂移[8]，出现积分误差。而加速度计虽然短时间内精度差，但长时间测量不会产生积分误差，所以可通过重力加速度在当前载体坐标系的分量与加速度计测得的当前重力加速度分量做向量积运算，修正陀螺仪引起的误差[9]。其中由公式（1）和公式（5）可得：

加速度计所测重力加速度经单位化后为 ，则加速度计对陀螺仪的修正误差为：

3 实验结果与分析

3.1 姿态解算实验结果分析

为便于控制器安装在前臂假肢上，本文所设计的前臂假肢手部自平衡系统将STM32、MPU6050、RS485等器件均集成在一块PCB电路板上，其实物图如图4所示。

图4 硬件实物图

为了测试互补滤波算法的性能，本文分别在静态和动态环境下对有/无互补滤波进行了姿态解算算法的测试和对比。

1）静态测试：将控制电路板水平静止放置在桌面上，采集姿态解算输出数据并对数据进行波形绘制，如图5所示。分别为比例系数和积分系数。

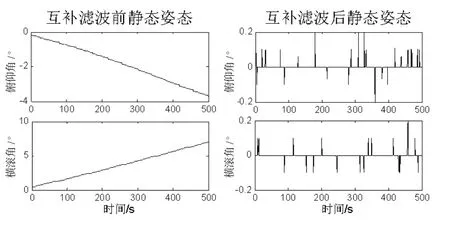
图5 互补滤波前后的静态测试对比

由图5可知，互补滤波前的姿态角会随着时间漂移，而互补滤波后的姿态角虽然有小范围波动，但基本保持在水平位置。

2）动态测试：将控制电路板进行俯仰和翻滚转动后水平放置在桌面上，其动作姿态波形如图6所示。

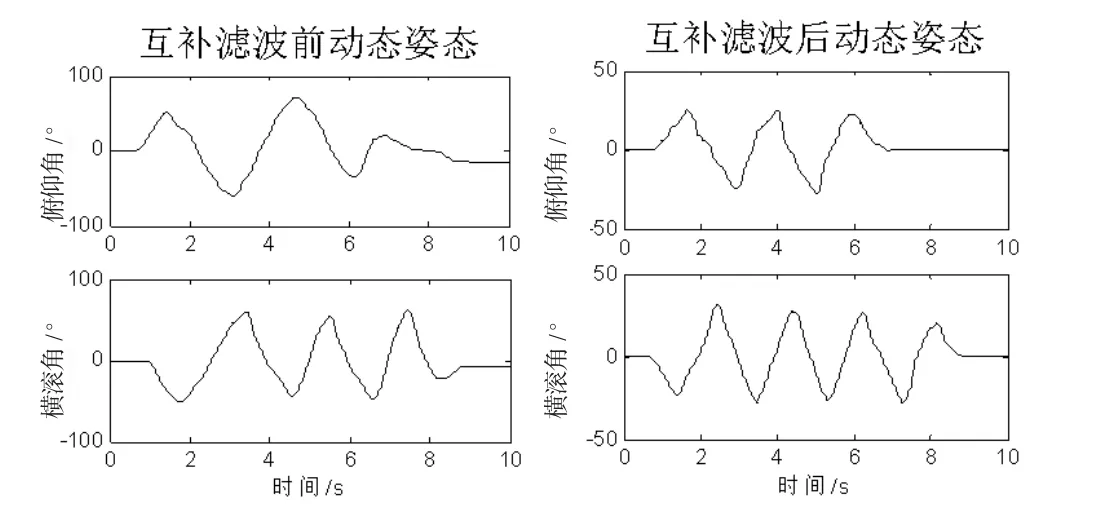
图6 互补滤波前后的动态测试对比

由图6可知，互补滤波前的姿态角经过一段时间转动后不能回到水平初始角度，而互补滤波后的姿态角经过一段时间转动后均能保持在水平初始角度。

3.2 前臂假肢手部自平衡系统实验结果分析

在上述实验的基础上，将控制电路板安装在前臂假肢上，对手部进行自平衡控制调试。调试步骤如下：首先向语音识别模块发出“自平衡”指令，指示灯点亮，前臂假肢进入手部自平衡模式，然后对假肢进行俯仰、横滚动作，观察手部虎口处是否处于水平状态。

经过测试，前臂假肢在进行俯仰、横滚动作时，手部虎口处一直保持水平状态，实验结果如图7所示。

图7 前臂假肢俯仰、横滚测试实验

4 结论

本文所介绍的前臂假肢手部自平衡系统采用互补滤波姿态估计算法，将加速度计和陀螺仪的数据进行互补融合，有效地补偿了因陀螺仪漂移造成的姿态误差，从而得到了精确、实时、可靠的姿态角度，并通过对前臂假肢姿态的跟踪和控制，成功实现了前臂假肢手部自平衡动作。

[[1]薛亮,苑伟政,常洪龙,等.用于微小型飞行器姿态估计的四元数扩展卡尔曼滤波算法[J].纳米技术与精密工程,2009,7(2)∶163-167.

[2]贾瑞才.基于四元数EKF的低成本MEMS姿态估计算法[J].传感技术学报,2014(1)∶90-95.

[3] 宋宇,翁新武,郭昕刚.基于四元数EKF算法的小型无人机姿态估计[J].吉林大学学报(理学版), 2015,53(3)∶511-518.

[4]梁延德,程敏,何福本,等.基于互补滤波器的四旋翼飞行器姿态解算[J].传感器与微系统,2011,30(11)∶ 56-58,61.

[5]邓正隆.惯性技术[M].哈尔滨∶哈尔滨工业大学出版杜,2006∶14-164.

[6]秦永元.惯性导航[M].北京∶科学出版社,2006∶287-305.

[7]关越魏,何波贤,于仁清,等.基于四元数解算陀螺仪姿态角算法的实现[J].电脑编程技巧与维护, 2015(9)∶32-34.

[8]樊炳辉,张凯丽,王传江,等.基于四元数的前臂假肢手部自平衡的设计[J].电子技术应用,2016,42(5)∶78-81.

[9]王立,章政,孙平.一种自适应互补滤波姿态估计算法[J].控制工程,2015,22(5)∶881-886.

[10]孙金秋,游有鹏,傅忠云.基于自适应显式互补滤波的姿态解算方法[J].测控技术,2015,34(4)∶24-27,31.