一种小型无人机动态磁罗盘校准方法评估

管沁朴 王田苗

(北京航空航天大学机械工程及自动化系，北京，100191)

0 引言

近年来，小型无人机以其结构简单、机动性能好、适应性强等特点，在航空摄影、电力巡线、地质勘查、农业植保及测绘等行业领域得到越来越广泛的应用[1]。目前，在有关测量小型无人机航向角的研究中，绝大部分采用磁罗盘方案来实现无人机的自主飞行及航线控制，磁罗盘通过测量地磁场为无人机提供方向信息。磁罗盘虽然存在测量精度低、对磁场环境较为敏感等缺点，但是由于其成本低、响应快、体积小、功耗低等优点，在精度要求不苛刻的小型无人机中得到了非常广泛的应用[2]。

由于磁罗盘容易受到环境以及无人机机体自身的电磁干扰，并且在制造过程中难免产生一定的误差，所以无人机在机体发生改变或环境发生变化时，都需要进行磁罗盘校准。传统的磁罗盘校准方法主要有3类[3]：采用神经网络方法与基准航向对比实现校准、采用冗余传感器等方式实现校准和采用磁罗盘自校准的方式。其中，磁罗盘自校准方式主要包括swing方法和椭圆（球）拟合法。

在上述3类传统的磁罗盘校准方法中，第一类方法很难在外场找到高精度航向基准；第二类方法则会大大增加系统成本；第三类方法中的椭圆（球）拟合法以其能在完全不增加成本的情况下实现高精度的校准，得到了广泛的应用。

小型无人机由于旋转方便，可以很方便的实现椭圆拟合方法，但是对操作要求较高，实际应用中很容易因为地磁方向的偏差和操作失误，造成校准结果偏差较大，导致无人机实际飞行时航向误差增大。

针对上述问题，本文在传统椭球拟合校准法基础上提出了一种动态评估校准进度的磁罗盘校准方法，能够有效规避由于操作不规范带来的校准失败风险，提高了校准结果的精度。

1 校准方案

目前，最常用的微型磁传感器主要由异向性磁阻传感器（Anisotropic MagnetoResistive,AMR）构成，该感应器件将敏感轴上的磁场强度转换成电压变化量，再由惠斯通桥测量出该电压的值，进而得到与磁场强度在敏感轴上分量成正比的测量结果。小型无人机由于经常需要做出一些大姿态机动动作，两轴磁罗盘不足以满足其使用要求，所以通常使用三轴传感器分别测量三个轴向的磁场强度，从而得到更精确的航向信息。

对于水平放置的磁罗盘来说，俯仰角和滚转角均不需要考虑，机体的磁航向角Ψ(使用标准机体坐标系，即x轴指向飞机正前方；y轴正方向指向飞机正右方；z轴指向飞机正下方)可用如下公式表示：

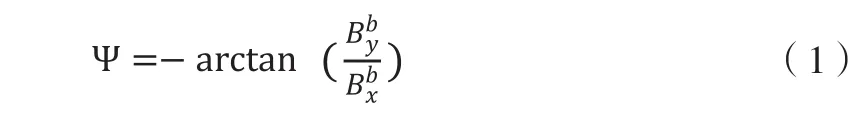
其中 代表飞机在机体坐标系下测量的y轴方向的磁感应强度(B)， 代表x轴方向分量。对于三轴磁罗盘，一般不能等效为水平放置，因此需要考虑俯仰角 和滚转角的影响。考虑到标准本体坐标系到导航坐标系的变换[4]，结合公式(1)，最终三轴磁罗盘航向角计算公式为：

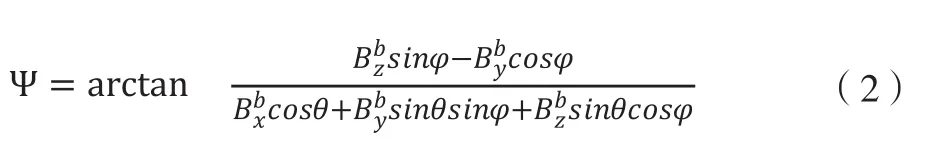
由公式(2)计算得到机体相对于地磁场的方向，与地理北方相差一个磁偏角常量。根据地磁图或插值法[5]查到当地磁偏角 后，可根据如下公式计算得到飞机的真北航向角：

一般小型无人机飞行距离较近，磁偏角不会在飞行过程中发生明显变化，因此该变量可以看作常量，由于其变化产生的误差不做进一步分析。

2 校准误差分析

由于磁罗盘在实际使用过程中会受到一系列不同类型的误差引起的干扰，从而造成测量结果出现一定的偏差，对无人机飞行及航线控制造成了不利影响。这些误差主要分为5类[6]：（1）测量比例系数误差 ，（2）测量轴安装角误差 ，（3）测量轴零偏误差 ，（4）硬磁干扰软磁干扰这些误差的产生原理及表现形式分别如图1和图2所示。

1）测量比例系数误差是由于不同传感器对于磁感应强度等比变换系数不一致而出现的误差，该系数体现了传感器对所测量磁场强度的灵敏度系数。对于三轴磁罗盘来说，该误差为一个3x1的向量。

2）测量轴安装角误差 是由于传感器三个测量轴在安装时不能保证绝对互相垂直，使得某一轴的测量结果中包含了其他轴上的分量。该误差为一个3x3的矩阵。

3）测量轴零偏误差 是由于传感器在外接磁感应强度为零时仍然输出非零值，从而造成测量结果偏移。该误差为一个3x1的向量。

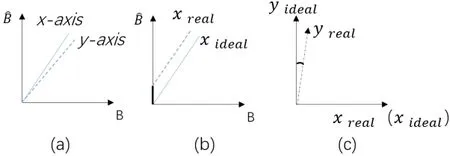
图1内部误差产生原理

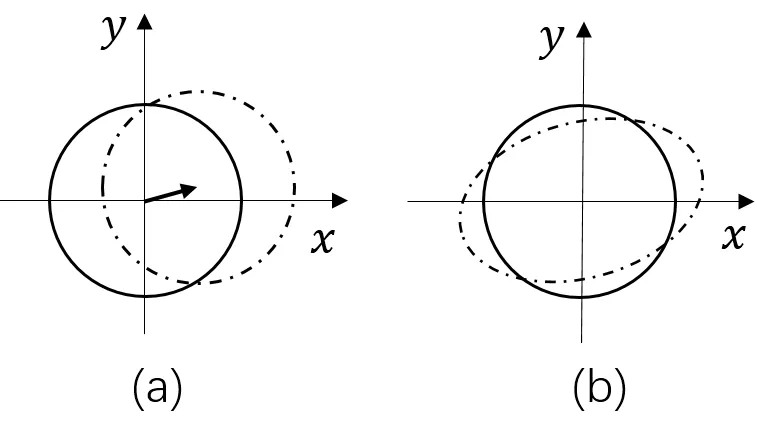
图2误差表现形式

图2 中两轴对应椭圆，三轴对应椭球。(a)表示硬磁干扰及零偏产生的干扰，表现为测量结果为偏置的正圆(球)；(b)表示软磁干扰及不同轴比例不同产生的干扰，表现为测量结果为椭圆(球)。

通过对上述误差进行分析，得到最终的观测公式为：

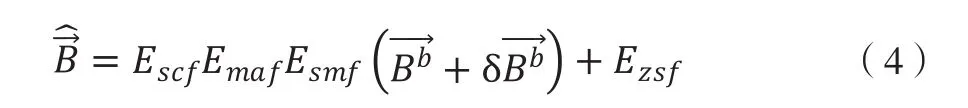
3 校准方法分析

通过对公式(4)进行分析总结，不能且没必要从观测结果区分零偏和硬磁干扰分别带来的偏移，因此可以用分别代表三个轴的测量结果零偏分别代表三个轴的总比例误差。在不考虑测量轴安装角度误差时，测量值可满足如下方程：

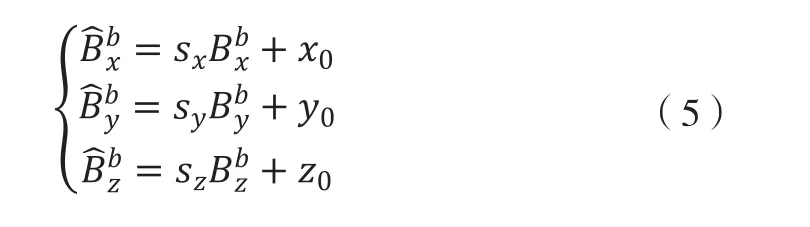
假设当地地磁场强度为 ，则满足如下方程：

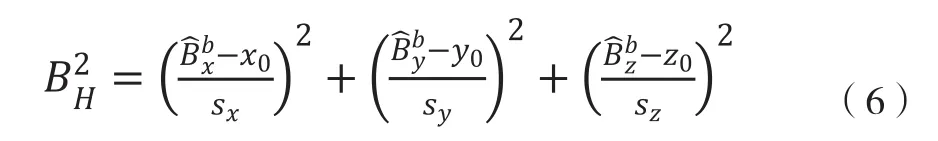
考虑到安装角度误差，假设x轴方向跟设定方向相同，y轴同x轴安装角误差为 ；z轴同x-z平面安装角误差为；z轴同y-z轴安装角度误差为 ，如图3所示。则式(5)可表示如下：

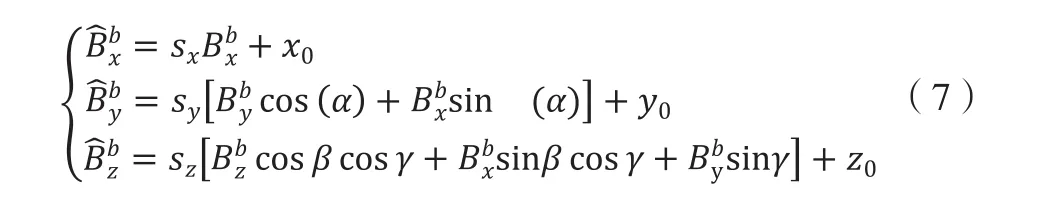
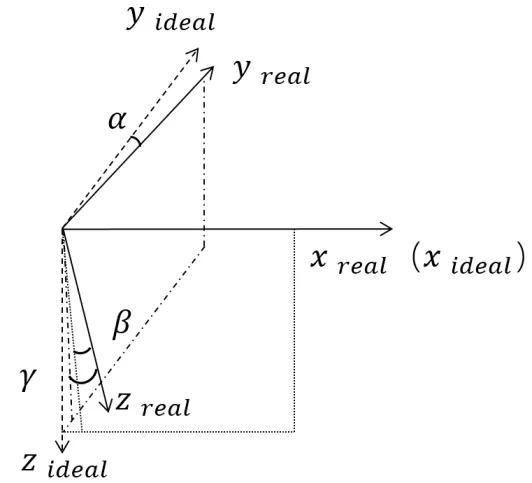
图3 安装角误差

将式（7）代入式（6）中，可以表示为如下变形椭球形式：

最终校准目标即找到一个最合适的 … 的估计值。为了方便计算，将式（8）改变为矩阵形式，如式（9）所示。

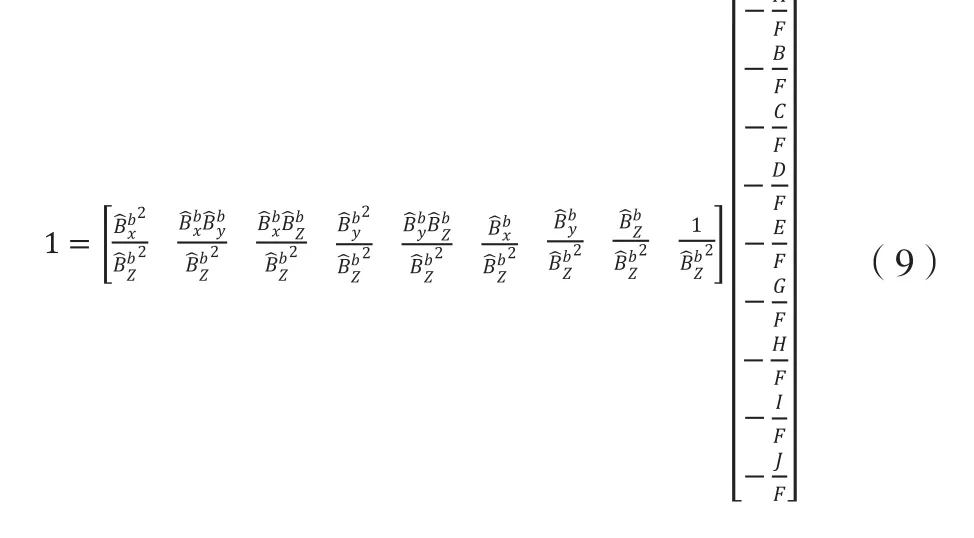
在同一次校准中，所有A-J参数都是常数，因此将所有的k次测量值均写成一个大的矩阵形式：

其中X为观测结果组成的矩阵，每一行由一次观测结果构成：

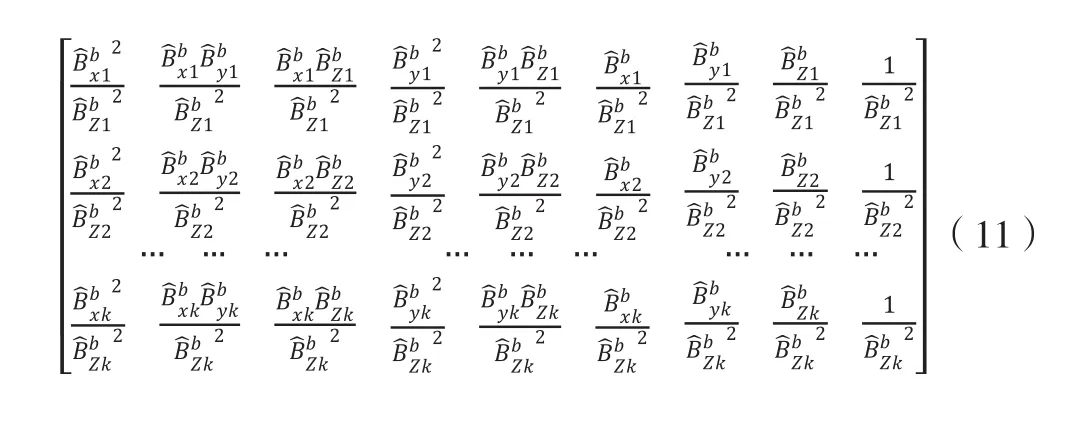
P为需要计算的椭球参数矩阵：

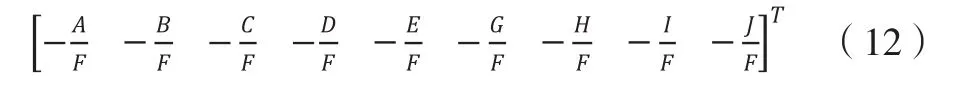
W为全1向量：

最后，按照最小二乘法估计的结果，椭球参数估计结果P 可按照如下方法进行计算：

现在，只需要采集至少9个测量点即可实现计算，得到P 值，进而计算得出和，将公式（7）简化后得到最终校准矩阵，如式（15）所示。其中代表校准后的测量数据；代表原始测量数据；代表软磁标准矩阵；为硬磁校准向量。

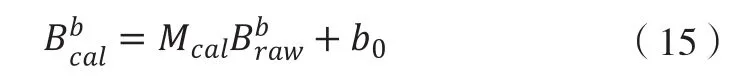
但在实际操作中，如果采集的点过于集中，则会出现估计结果偏差较大甚至校准失败的问题。为了解决该问题，并适当降低计算量，本文制定了以下策略进行数据的采集和评估。

1）将采集的数据按照形心分为8个卦限，设定每个卦限最少数据量。

2）将采集数据加入已有的数据组中。

3）更新已有数据形心，评估目前8个卦限中是否都满足设定的最小数据量要求。

4）如果某个卦限达到要求则不再添加数据；如果卦限数据量不足则继续进行步骤2；全满足则进行下一步。

5）根据公式（14）计算拟合椭圆的代数方程，进而得到校准矩阵，校准结束。

6）利用公式（15）对采集到的数据进行计算，得到校准后的数据，进而利用公式（3）算出飞机的真北航向角。

4 实验结果分析

4.1 校准实验

针对本文设计的校准步骤，首先通过模拟磁罗盘数据生成过程并加入误差生成仿真数据，再选取一定数量的测试点进行校准计算，然后对比计算结果、验证算法的可行性以及选取校准数据量对校准精度的影响。

通过对仿真数据进行校准计算，进而生成原始数据，如图4所示，测量结果有一定误差且分布在一个椭球体表面附件。

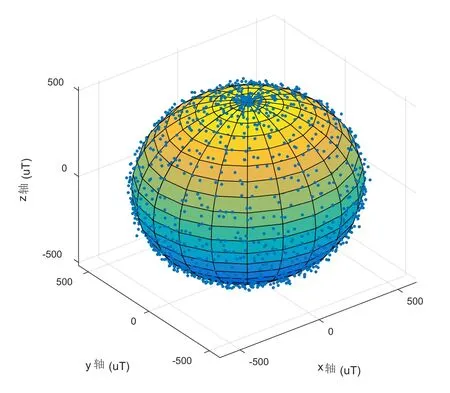
图4 通过模拟生成的直接测量结果

4.2 校准结果

根据本文提出的计算策略，设定不同的数据量对飞机航向角进行校准，校准后得到飞机航向角误差对比如图5所示。

通过对校准结果进行对比表明：在数据量较少的情况下，由于每个卦限都保证有一定数量的点，依然能准确计算出飞机航向角(均值误差在1°以内）；适度提高选取的数据量，可以在一定区间内显著提高飞机航向角计算结果的准确性和稳定性；选取足够多的数据量之后再增加数据量，飞机航向角计算结果的精度没有明显提升。

5 结论

本文设计的磁罗盘校准方法能够有效地实现小型无人机的校准精度，防止因操作不当、采集数据过于集中而出现校准误差过大；通过对不同校准数据量进行对比，选取最优区间，提高了校准结果的精度。最后，通过仿真分析及实验，验证了该方法的可行性和有效性。

图5 不同校准结果计算得到的航向角误差对比

[1]蔡健.各国无人机应用及发展概览[J].中国安防, 2016(9)∶91-103.

[2] 王恺.小型固定翼无人机飞行控制系统的实现[D].北京：北京工业大学,2013.

[3]孙宏伟,房建成,李艳.椭圆拟合方法在磁罗盘罗差校准中的应用[J].光学精密工程,2009,17(12)∶3034-3039.

[4]蔡体菁,刘莹,宋军,等．嵌入式/GPS/MIMU磁罗盘组合导航系统[J]．仪器仪表学报,2010,31(12)∶ 2695-2699.

[5]周伟静,沈怀荣．一种利用磁偏角地磁图自动计算磁偏角的方法[J]．测绘工程,2007,16(1)∶51-54.

[6] Foster C C, Elkaim G H.Extension of a Two-StepCalibration Methodology toIncludeNonorthogonalSensorAxes.IEEE Transactions on Aerospace and Electronic Systems[J].2008,44(3)∶1070-1078.