加劲环和子午肋对超大型冷却塔施工过程风致稳定性能和极限承载力的影响

柯世堂，徐璐，朱鹏



加劲环和子午肋对超大型冷却塔施工过程风致稳定性能和极限承载力的影响

柯世堂，徐璐，朱鹏

(南京航空航天大学 土木工程系，江苏 南京，210016)

为研究内部加劲环和外部子午肋对超大型冷却塔施工过程风致稳定性的影响，以国内某电厂在建的高度为220 m的超大型冷却塔为研究对象，针对光滑塔、加肋塔、加环塔和加肋加环塔4种设计方案，分别进行考虑内吸力、施工荷载、混凝土龄期实时变化的冷却塔施工全过程整体、局部稳定性及极限承载力对比分析。在此基础上，研究加劲环和子午肋对施工期超大型冷却塔风致稳定性能的影响规律。研究结果表明：加劲环可有效提高冷却塔施工全过程的屈曲稳定性，但对结构的局部稳定性不利；布设子午肋导致结构施工全过程屈曲稳定性和极限承载力降低，但可提高结构的局部稳定性；布置加劲环和子午肋可显著改善冷却塔整体、局部和施工全过程屈曲稳定性能及极限承载力。

超大型冷却塔；加劲环；子午肋；极限承载力

随着火力发电设备容量的不断增大，与之配套的冷却塔规模也日益增大，进而涌现出一批超规范高度限值[1−2](190 m)的超大型冷却塔。伴随着冷却塔高度和直径的增加，风致稳定性问题愈加突出。因此，如何通过改变冷却塔构造以提高结构的稳定性能和承载力成为冷却塔抗风设计亟待解决的问题之一[3−6]。与此同时，超大型冷却塔施工周期和难度也日益增大，混凝土强度及弹性模量随着施工进度而实时变化，导致整个施工和运营阶段其稳定性和承载力也随施工进度不断改变，因此，有必要对此类超大型冷却塔施工过程中的材料和结构性能进行深入分析。自1965年英国渡桥电厂冷却塔风致倒塌事故以来，人们采用有限元法[7−10]对大型冷却塔的局部和整体稳定性进行了大量研究，为同时期冷却塔结构的抗风设计提供了技术支持。此前，柯世堂等[11]基于风洞试验和有限元方法对开孔的超大型排烟冷却塔采取了有效的加固方案，并计算了整体线性稳定性和施工状态极限承载力，其研究结果可为超大型排烟冷却塔稳定性分析提供参考。周旋等[12]分析了英国渡桥电厂冷却塔倒塌的塔型因素，对比了塔型对冷却塔风致响应的影响规律，为此类冷却塔塔型的选取提供依据。邹云峰等[13]研究了超大型冷却塔单塔外表面风荷载三维效应，将风洞试验获得的三维风压下冷却塔的屈曲模态与规范风压下冷却塔屈曲模态进行对比，为后续冷却塔屈曲分析提供技术支持。然而，已有研究并未系统地分析加劲环和子午肋对超大型冷却塔风致稳定性能影响的规律，特别是针对超大型冷却塔施工全过程整体稳定性能和极限承载力的研究较少。为此，本文作者以西北地区某在建220 m超高大型冷却塔为研究对象，采用4种设计方案分别进行整体、局部和施工全过程稳定性及极限承载力分析，研究加劲环和子午肋对超大型冷却塔风致稳定性能和承载力的影响规律，为此类超大型冷却塔加环和加肋措施的选取提供参考依据。

1 工程概况

该在建超大型冷却塔位于西北地区，属于B类地貌，50年一遇基本风压为0.35 kN/m2，相应的风速为23.7 m/s。冷却塔塔高为220 m，喉部高度为165 m，进风口高度为30.75 m，塔顶中面直径为128.10 m，喉部中面直径为123.00 m，底部直径为185.00 m；塔筒壁厚沿高度呈指数变厚，最小壁厚为0.38 m，最大壁厚为1.85 m。

本文采用4种设计方案，分别为光滑塔、加肋塔、加环塔和加肋加环塔。其中加环塔塔筒喉部以下共设置3道加劲环，沿高度方向厚度均为0.40 m；沿半径方向厚度分别为0.71，0.72和0.74 m；加劲环所处高度分别为72.75，94.80以及139.43 m。加肋塔共沿塔筒环向均匀布置104条子午向加劲肋，肋条梯形截面高度和宽度分别为0.150 m和0.175 m，具体结构示意图如图1所示。

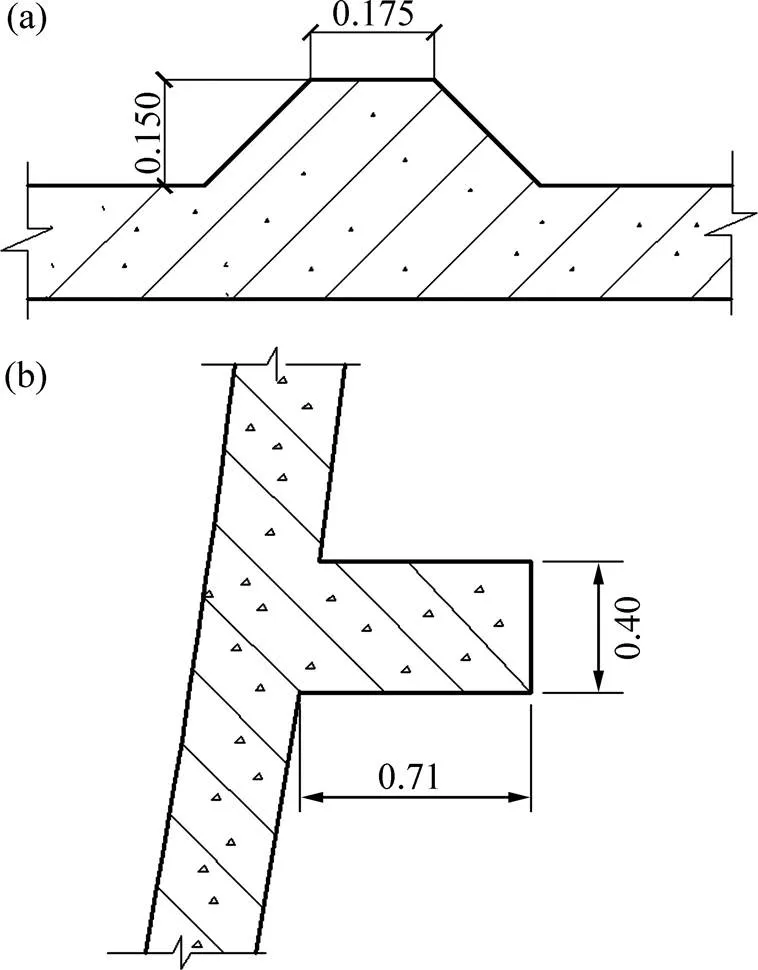
(a) 子午肋；(b) 加劲环

2 整体稳定性分析

根据“工业循环水冷却设计规范”[2]，冷却塔整体临界风压的计算公式如下：

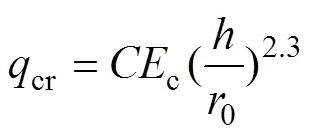
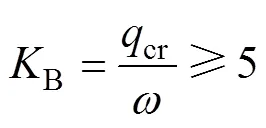
式中：cr为四塔塔筒屈曲临界压力；为经验系数，=0.052；c为混凝土弹性模量；为塔筒喉部壁厚；0为塔筒喉部半径；B为塔筒整体稳定安全系数；为塔顶风压标准值；H为风压高度变化系数；为风振系数；g为塔群系数；0为基本风压。

本研究中冷却塔塔筒混凝土强度等级为C40，其余条件如下：c为3.25×1010Pa；0为61.50 m，塔筒喉部壁厚为0.38 m；50年一遇基本风压为 0.35 kN/m2，相应风速为23.7 m/s。计算得到cr为14.03 kPa，B=6.55(大于5.00)，满足规范要求。

实际上，由于4种设计方案冷却塔均采用相同线型和壁厚，因此，基于规范获得的塔筒整体稳定安全系数一致，但这与实际情况不符。因为增设加劲环后塔筒整体刚度必然提高，其稳定性也将有所变化，故后续有必要通过有限元分析进行冷却塔的施工全过程屈曲稳定性、局部稳定性和极限承载力分析。

3 施工全过程屈曲稳定性分析

3.1 有限元建模及动力特性分析

建立6个典型施工高度的冷却塔有限元模型，分别为工况1(15层模板)、工况2(35层模板)、工况3(55层模板)、工况4(75层模板)、工况5(95层模板)和工况6(128层模板)。其中，塔筒采用Shell63单元，环向和子午向分别划分为256和128个单元；环基及与环基连接的64对X型柱均采用Beam188单元；X型支柱与塔筒下部连接采用节点自由度耦合的方式，每个环基下部采用Combin14单元，每根桩基均采用3个力弹簧单元和3个力矩弹簧单元以分别模拟桩沿竖向、环向、径向、绕竖向、绕环向和绕径向的作用。弹簧单元一端与环基刚性连接，另一端固结约束。加劲环和子午肋均采用Shell63单元。

基于有限元模型对4种设计方案冷却塔进行动力特性分析。图2所示为4种设计方案中冷却塔不同施工高度下前100阶频率分布及6个典型施工高度下的冷却塔有限元模型图。由图2可知：不同施工高度下4种类型冷却塔自振频率变化趋势基本一致，但随施工高度的增加自振频率逐渐减小。其中，在工况1中的施工高度处，不同阶数自振频率波动较大，而自35层模板高度以上自振频率波动较小且呈线性趋势增长；同时，自35层模板高度以上，4种类型冷却塔自振频率出现差异，布设加劲环的2座冷却塔自振频率明显高于光滑塔和加肋塔的自振频率。

(a) 工况1；(b) 工况2；(c) 工况3；(d) 工况4；(e) 工况5；(f) 工况6

3.2 施工全过程屈曲稳定分析

在施工过程中，冷却塔混凝土强度随时间逐步增长，新浇筑的混凝土强度较弱[14−15]，因此，需要对在施工过程中风荷载及施工荷载作用下的冷却塔稳定性进行研究，以控制施工进度。在计算过程中，施工速度均按每天建1层模板考虑，并根据规范[2]按照如下标准选取不同龄期的混凝土弹性模量：

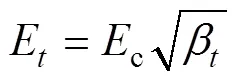
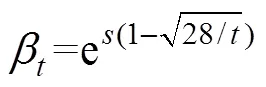
对不同施工阶段的冷却塔分别施加光滑和加肋塔后2种粗糙度下的规范风压，如图3所示。考虑塔群系数(D=1.2)，分别进行屈曲分析并获取该工况下冷却塔整体失稳的屈曲系数，进而获得对应施工高度下冷却塔的极限承载能力即临界风速。

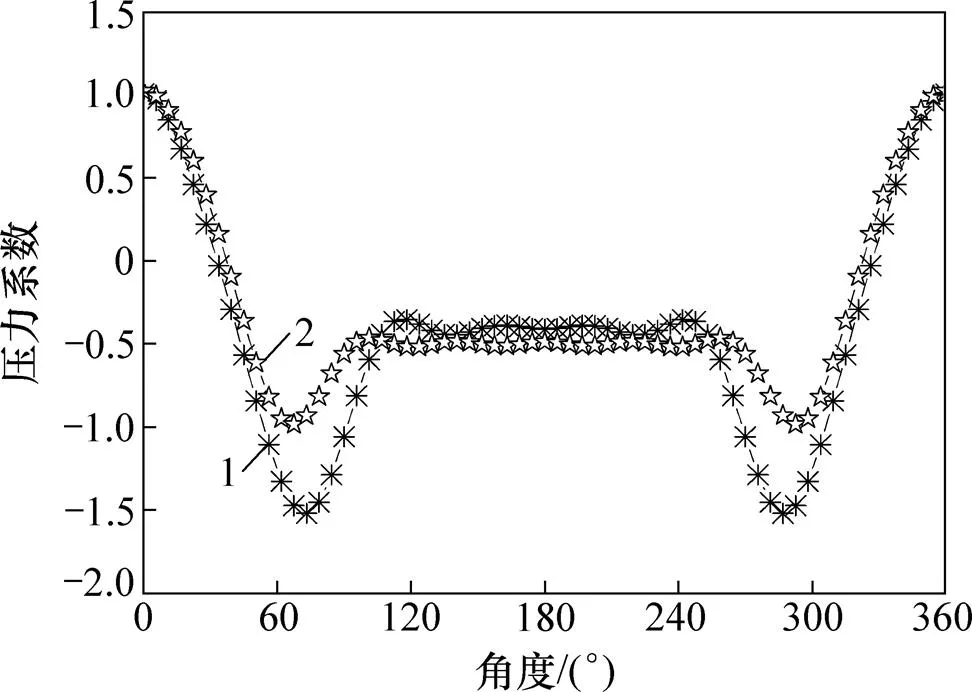
1—规范无助塔压力系数曲线；2—规范加肋塔压力系数曲线。

现行规范只要求在验算结构局部稳定时考虑内吸力，并未提及在验算施工全过程稳定性时需考虑内吸力。本文以光滑塔为例，分别对考虑内吸力和混凝土龄期及施工荷载、考虑内吸力不考虑混凝土龄期及施工荷载、不考虑内吸力考虑混凝土龄期及施工荷载、不考虑内吸力和混凝土龄期及施工荷载的冷却塔进行施工全过程屈曲稳定验算，获得不同工况下光滑塔临界风速和最大位移，如图4所示。

表1所示为4种冷却塔典型高度最大位移对比。由表1可知同时考虑内吸力和混凝土龄期及施工荷载为屈曲稳定的最不利工况，故后面4种设计方案冷却塔将以最不利工况(考虑内吸力和混凝土龄期)作为研究对象，以分析加劲环和子午肋对冷却塔施工全过程屈曲稳定的影响。

图5所示为4种冷却塔考虑内吸力和混凝土龄期及施工荷载下不同施工高度屈曲临界风速及屈曲模态对比。表2所示为4种冷却塔典型高度临界风速对比。由图5和表2可知：1) 加劲环有利于提高结构施工过程稳定性，增大屈曲临界风速，减小风致响应；子午肋导致结构屈曲临界风速减小，使得风致响应大幅增加，不同高度下冷却塔最大位移变化趋势发生改变。2) 4种塔屈曲临界风速均随施工模板层数增加而减小，但自喉部至塔筒顶部临界风速降幅增大，加肋塔和加肋加环塔降幅均在10%左右，光滑塔和加环塔降幅超过11%。3) 加肋塔和加肋加环塔风致响应最大值的出现区域随施工高度的增加而从支柱与塔筒连接区域逐渐上移至塔筒顶部，且风致响应位移最大值也逐渐增加；但光滑塔和加环塔风致响应最大值的出现区域随施工高度的增加而由支柱与塔筒连接区域逐渐上移至喉部附近，且风致响应位移最大值也逐渐增加，但自喉部至塔顶位置逐渐减小。

1—考虑内吸力和龄期的临界风速；2—考虑内吸力的临界风速龄期最大位移；3—考虑内吸力不考虑龄期的临界风速；4—考虑内吸力不考虑龄期最大位移；5—不考虑内吸力考虑龄期的临界风速；6—不考虑内吸力考虑龄期最大位移；7—不考虑内吸力不考虑龄期的临界风速；8—不考虑内吸力不考虑龄期最大位移。

表1 4种冷却塔典型高度最大位移对比

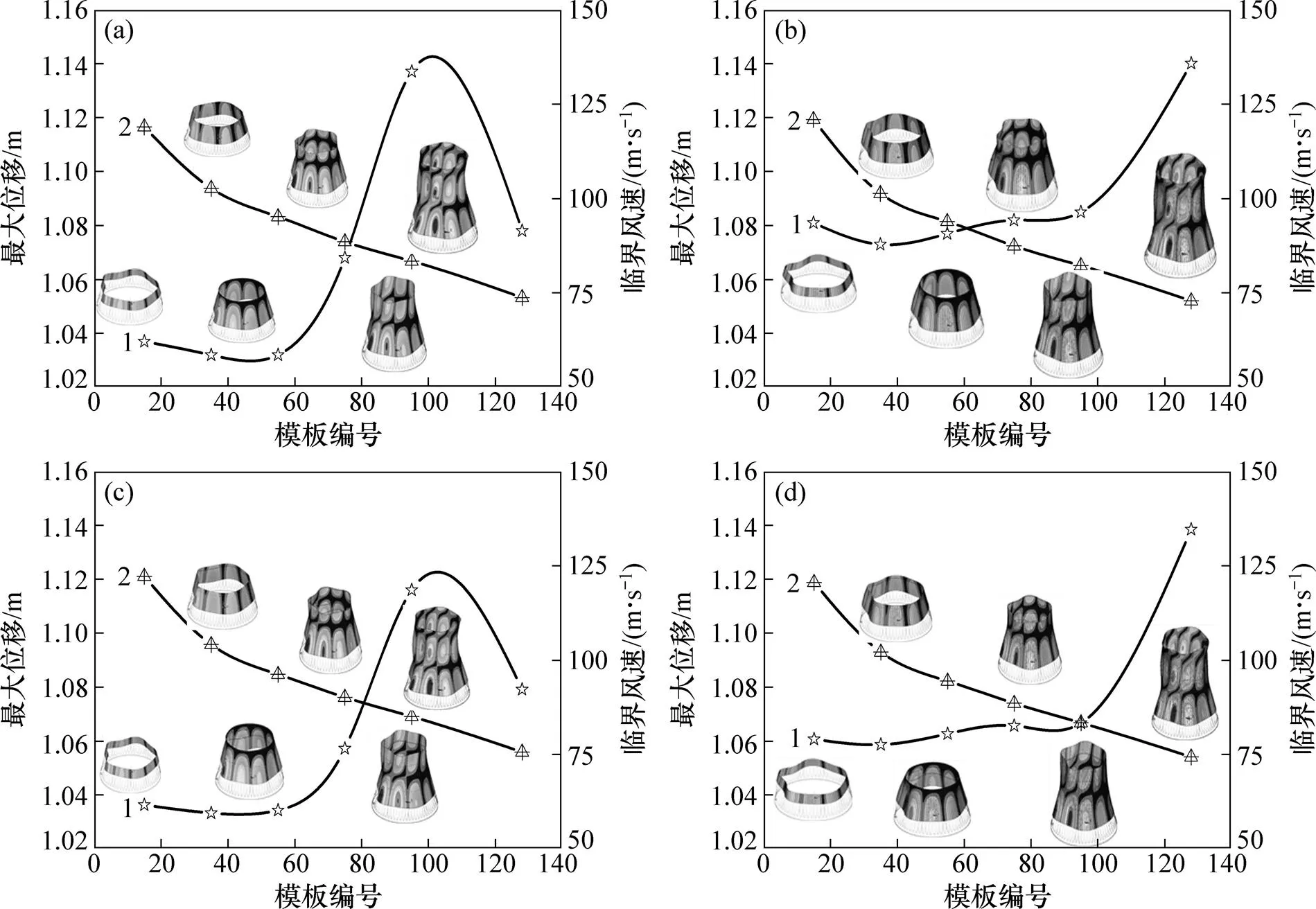
(a) 光滑塔；(b) 加肋塔；(c) 加环塔；(d) 加肋加环塔

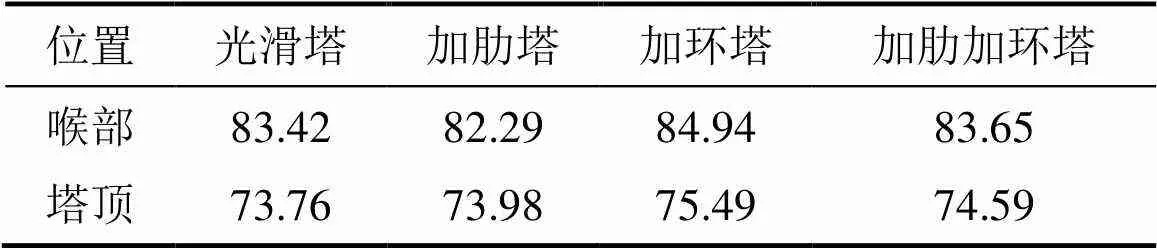
表2 4种冷却塔典型高度临界风速对比

4 极限承载力分析

比较多种工况条件下冷却塔施工全过程在风荷载作用下的极限承载力，并以光滑塔为例计算考虑混凝土龄期和内吸力时的结构极限承载力。图6所示为不同计算工况下光滑塔最大位移及位移梯度随风速变化示意图。在不同风速下同时考虑混凝土龄期和内吸力的冷却塔最大位移最大，故后续以最不利工况(考虑混凝土龄期和内吸力)为例进行分析。以10 m高度处23.7 m/s的初始风速为基础进行逐级加载，加载风速步长为1~20 m/s。当风速增大至混凝土受拉破坏(C40混凝土抗拉强度tk≥1.71 MPa)时，局部区域混凝土开裂，钢筋受拉；随着风速进一步增大，塔筒受压区接近极限受力状态(C40混凝土抗压强度ck≥19.1 MPa)，冷却塔风致响应显著增大，此时可由最大位移随风速变化确定极限承载状态。

图7所示为冷却塔各典型施工阶段最大位移及位移梯度随风速变化示意图。由图7可知：子午肋对冷却塔极限承载力影响显著，各工况下布设子午肋的冷却塔在不同风速下的最大位移均小于光滑塔和加环塔的最大位移，说明子午肋在改变塔筒风压分布模式的同时使得塔筒变形显著减小，但加肋塔冷却塔的极限承载力明显低于未加肋冷却塔的极限承载力。布设加劲环对冷却塔塔筒最大位移影响微弱，随施工高度增加，其极限承载力与加肋塔的越接近，失稳临界风速显著减小。成塔时为极限承载力最不利工况，加环塔和加肋塔失稳临界风速降低至120 m/s，而加肋加环塔临界失稳风速为140 m/s，加肋塔的位移梯度较加环塔位移梯度小，但在成塔状态下，加肋加环塔失稳临界风速最大，位移梯度最小，承载性能最佳。

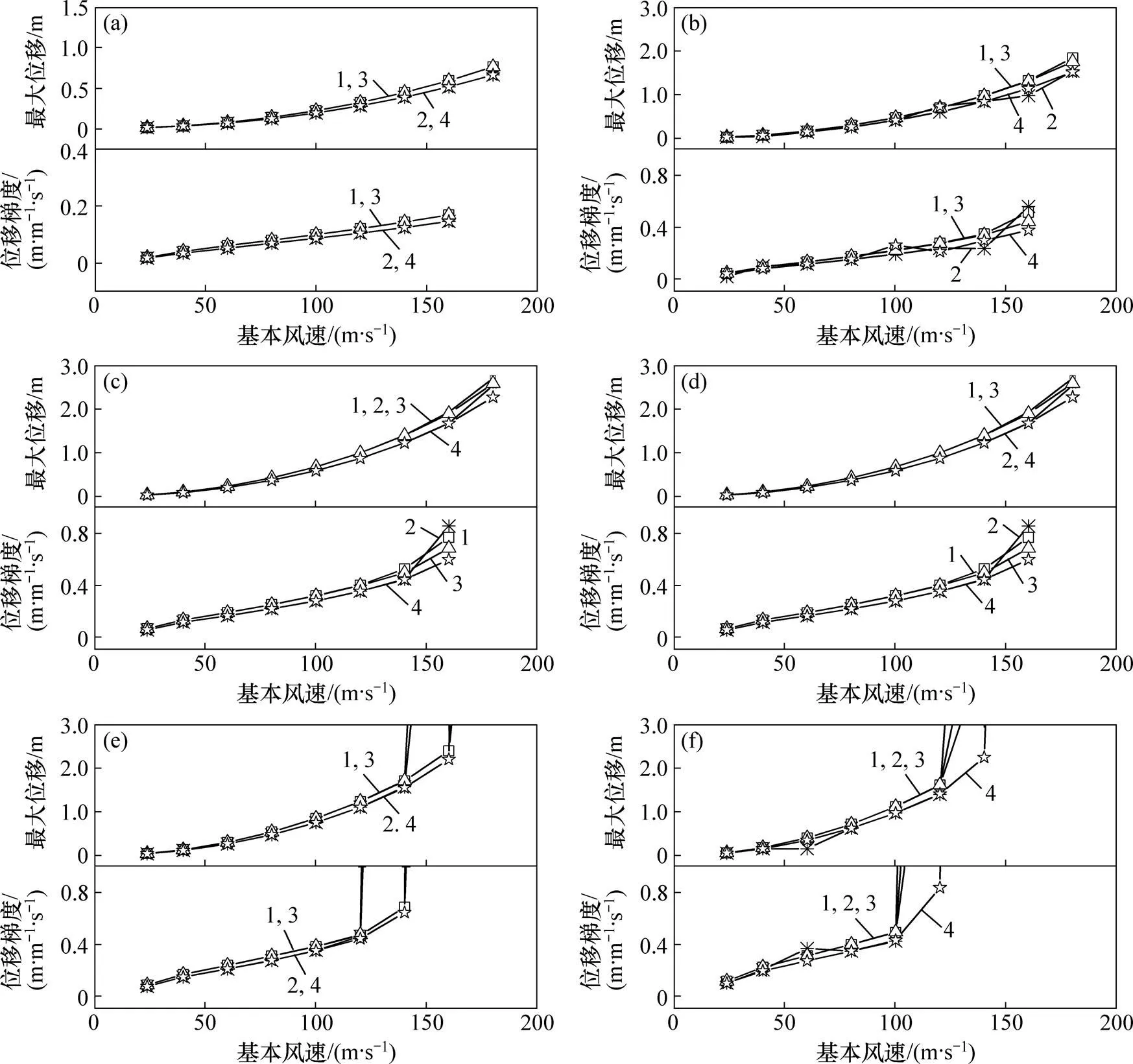
(a) 工况1；(b) 工况2；(c) 工况3；(d) 工况4；(e) 工况5；(f) 工况6

5 局部稳定性分析

冷却塔是一种空间薄壳结构，其稳定性是设计必须考虑的因素，根据“工业循环水冷却设计规范”[2]，冷却塔的局部稳定性计算公式如下：

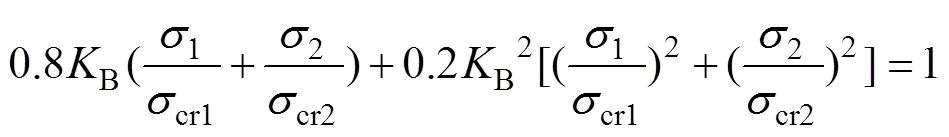
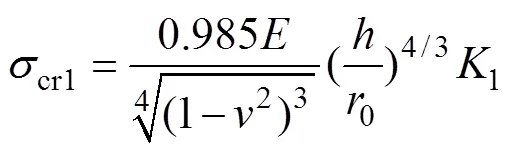
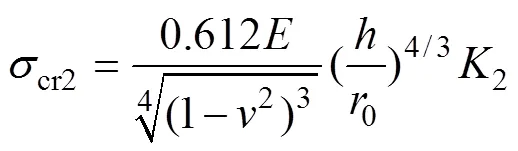
式中：1和2为不同荷载组合工况下的环向和子午向压应力；cr1为环向临界压力，cr2为子午向临界压力；和分别为壳体混凝土的弹性模量和泊松比；1和2可根据塔筒计和参数插值得到，本文4座冷却塔取1=0.232 3，2=1.250 6；B为局部稳定因子，规范要求B需大于5.00。

现行规范[2]要求局部稳定验算需考虑内吸力。图8所示为不考虑混凝土龄期及施工荷载下4种冷却塔局部稳定因子对比，图9所示为4种冷却塔不同高度最小局部稳定因子三维等势线图。由图8~9可知：考虑和不考虑混凝土龄期及施工荷载时4种冷却塔最小局部稳定因子变化规律一致，但考虑混凝土龄期及施工荷载时4种冷却塔局部稳定因子均大于未考虑混凝土龄期及施工荷载的4种冷却塔的局部稳定因子，故后续将以最不利工况(不考虑混凝土龄期及施工荷载)进行冷却塔的局部稳定性分析。

由图8可知：4种冷却塔的最小局部稳定因子在喉部以下较小且处于临界状态，而自喉部至塔顶位置逐渐增大，故后续只分析塔筒喉部以下的最小局部稳定因子。图10所示为4种冷却塔最小局部稳定因子三维等势线图。由图10可知：1) 4种冷却塔不同高度下的最小局部稳定因子均以0°子午线为中心呈对称分布。塔底局部稳定因子较大，随高度增加局部稳定因子逐渐减小。2) 加肋塔和加肋加环塔最小局部稳定因子三维等势线分布规律一致，未布设子午肋的其他2种冷却塔的分布规律也一致。布设子午肋是导致冷却塔背风面分布出现差异的主要原因，最小局部稳定因子显著增大。3) 加劲环的布设不利于结构的局部稳定性，加环塔整塔最小局部稳定因子(5.82)比光滑塔(5.86)的小；子午肋的增设可提高结构的局部稳定性，加肋塔整塔最小局部稳定因子(6.19)较光滑塔的增大5.6%；4) 4种设计方案冷却塔最小局部稳定因子对应的角度较接近，均出现在50~140 m处，由此可以看出冷却塔中下部是导致失稳的关键位置，但加肋塔最小局部稳定因子对应的高度比其余3种冷却塔的大。

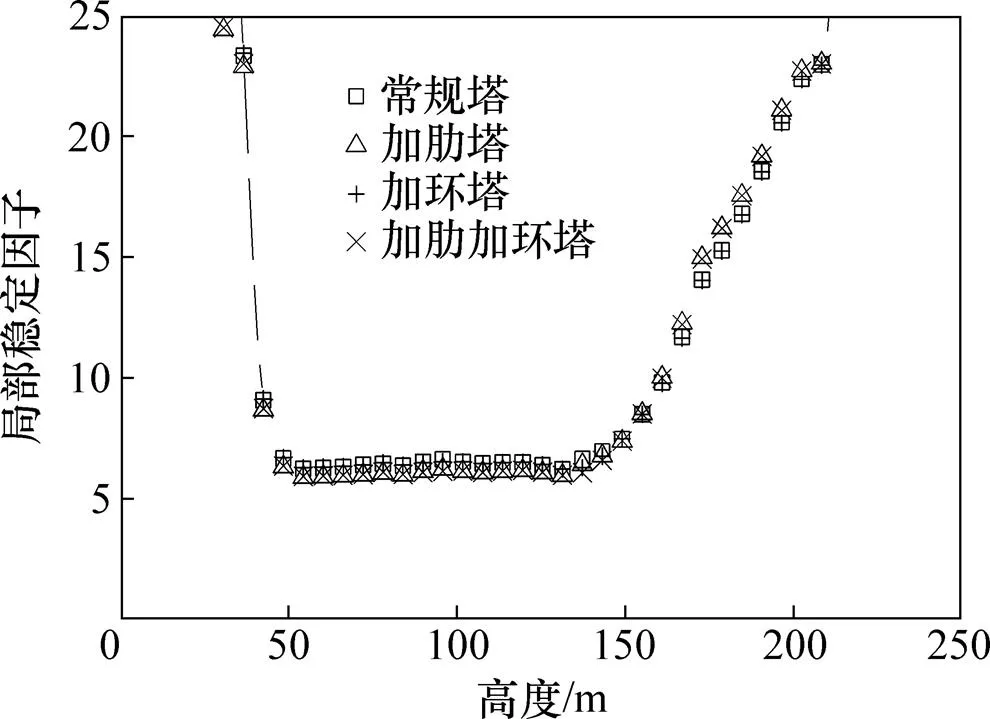
图8 不考虑混凝土龄期及施工荷载下4种冷却塔局部稳定因子对比

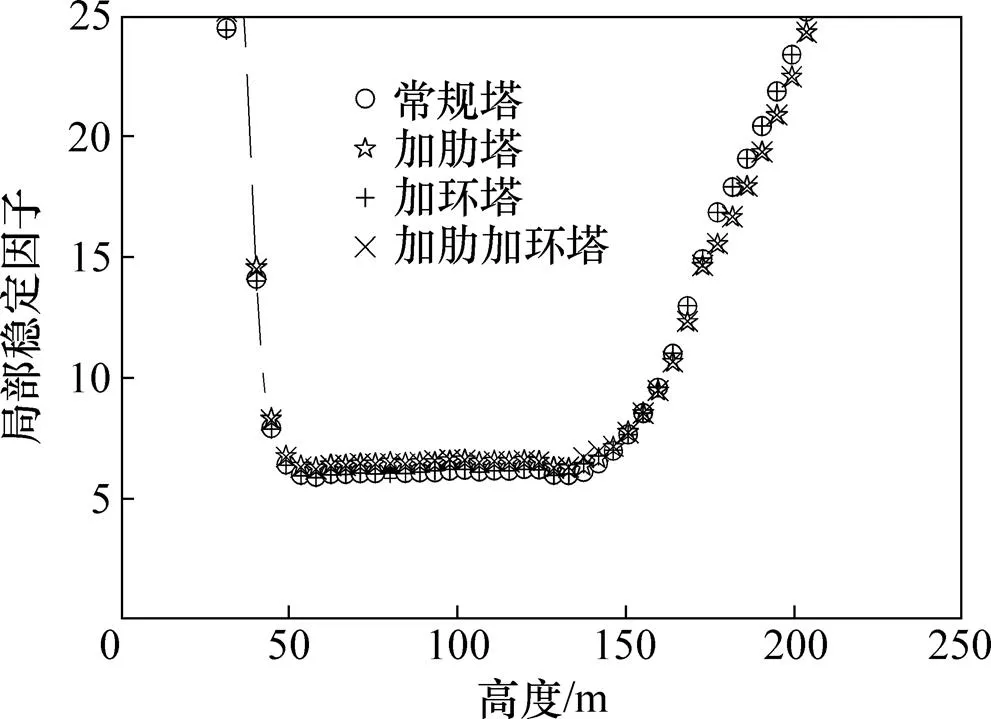
图9 考虑混凝土龄期及施工荷载下4种冷却塔局部稳定因子对比

(a) 光滑塔；(b) 加肋塔；(c) 加环塔；(d) 加肋加环塔

6 结论

1) 4种冷却塔自振频率受施工高度影响较大，随着施工高度增加其增幅逐渐减缓。加劲环可显著提高结构自振频率，而子午肋会导致结构自振频率降低。

2) 4种冷却塔基于文献[2]获得的塔筒整体稳定安全系数一致(B=6.55，B大于5.00)，考虑到增设加劲环后塔筒整体刚度必然提高，其稳定性也将相应增大，故需通过有限元方法对冷却塔的施工全过程屈曲稳定性和局部稳进行定性分析。

3) 考虑内吸力、混凝土龄期及施工荷载导致冷却塔整体屈曲稳定性降低，增设加劲环对结构的屈曲稳定性产生有利影响，但子午肋的布设导致结构屈曲临界风速减小，并提高风致响应最大值发生高度。综合认为加环塔的整体屈曲稳定性最好，加肋加环塔次之，加肋塔为最不利方案。

4) 加肋塔和加环加肋塔在不同风速下最大位移均比光滑塔和加环塔的小，但其失稳临界风速相对较小。随施工高度增加，加环塔的极限承载力与加肋塔的越接近，加肋加环塔承载性能最佳。

5) 在不同高度下，最小局部稳定因子均以0°子午线为中心呈对称分布，加肋塔和加环加肋塔最小局部稳定因子三维等势线分布规律一致，未布设子午肋的2种冷却塔的分布规律也一致。加劲环的布设不利于结构的局部稳定性，但子午肋的增设可提高结构的局部稳定性。经综合认为加肋塔局部稳定性最好，加肋加环塔次之，加环塔为最不利方案。

[1] DL/T 5339—2006, 火力发电厂水工设计规范[S]. DL/T 5339—5339, Power plant hydraulic design specification[S].

[2] GB/T 50102—2014, 工业循环水冷却设计规范[S]. GB/T 50102—2014, Industrial circulating water cooling design specification[S].

[3] 柯世堂, 杜凌云. 不同气动措施对特大型冷却塔风致响应及稳定性能影响分析[J]. 湖南大学学报(自然科学版), 2016, 43(5): 79−89. KE Shitang, DU Lingyun. Different aerodynamic measures of super large cooling tower wind-induced response and stable performance impact analysis[J]. Journal of Hunan University(Natural Science Edition), 2016, 43(5): 79−89.

[4] 张军锋, 葛耀君, 赵林. 基于风洞试验的双曲冷却塔静风整体稳定研究[J]. 工程力学, 2012, 29(5): 68−77. ZHANG Junfeng, GE Yaojun, ZHAO Lin. Study on global aerostatic stability of hyperboloidal cooling towers based on the wind tunnel tests[J]. Journal of Engineering Mechanics, 2012, 29 (5): 68−77.

[5] 卢红前. 大型双曲线冷却塔施工期风筒强度及局部稳定验算[J]. 武汉大学学报(工学版), 2007, 40(S1): 414−419. LU Hongqian. Large hyperbolic cooling tower construction intensity of ram and local stability calculation[J]. Journal of Wuhan University (Engineering Science), 2007, 40(S1): 414−419.

[6] 秦文科, 陈明祥, 周剑波. 基于有限元的双曲线型冷却塔结构强度及稳定性分析[J]. 武汉大学学报(工学版), 2012, 45(S1): 209−212. QIN Wenke, CHEN Mingxiang, ZHOU Jianbo. Based on the elliptic cooling tower structure strength and stability of the finite element analysis[J]. Journal of Wuhan University (Engineering Science), 2012, 45(S1): 209−212.

[7] KE S T, GE Y J, ZHAO L, et al. Stability and reinforcement analysis of super large exhaust cooling towers based on a wind tunnel test[J]. Journal of Structural Engineering, 2015, 14(12): 601−615.

[8] LANGHAAR H L, BORESI A P, MILLER R E, et al. Stability of hyperboloidal cooling tower[J]. Journal of the Engineering Mechanics Division, 1970, 96(5): 753−779.

[9] MANG H A, FLOEGL H, TRAPPEL F, et al. Wind-loaded reinforced-concrete cooling towers: buckling or ultimate load[J]. Engineering Structures, 1983, 5(3): 163−180.

[10] 赵林, 李鹏飞, 葛耀君. 等效静风荷载下超大型冷却塔受力性能分析[J]. 工程力学, 2008, 25(7): 79−86. ZHAO Lin, LI Pengfei, GE Yaojun. Equivalent load no super large cooling tower under the force bearing performance analysis[J]. Journal of Engineering Mechanics, 2008, 25(7): 79−86.

[11] 柯世堂, 赵林, 张军锋, 等. 电厂超大型排烟冷却塔风洞试验与稳定性分析[J]. 哈尔滨工业大学学报, 2011, 43(2): 114−118. KE Shitang, ZHAO Lin, ZHANG Junfeng, et al. Power plant large exhaust cooling tower wind tunnel test and stability analysis[J]. Journal of Harbin Institute of Technology, 2011, 43(2): 114−118.

[12] 周旋, 牛华伟, 陈政清, 等. 大型冷却塔风荷载干扰系数的取值方法[J]. 中南大学学报(自然科学版), 2014, 45(10): 3637−3644. ZHOU Xuan, NIU Huawei, CHEN Zhengqing, et al. Large cooling tower wind load value of interference coefficient method[J]. Journal of Central South University (Science and Technology), 2014, 45(10): 3637−3644.

[13] 邹云峰, 牛华伟, 陈政清. 超大型冷却塔单塔外表面风荷载三维效应及其设计取值[J]. 振动与冲击, 2013, 32(24): 24−30. ZOU Yunfeng, NIU Huawei, Chen Zhengqing. Super large cooling tower three-dimensional effect and a single pylon outside surface wind load design value[J]. Journal of Vibration and Shock, 2013, 32(24): 24−30.

[14] 黄刚, 陈朝. 某火力发电厂9000 m2冷却塔施工期整体稳定性分析[J]. 特种结构, 2015, 32(6): 27−29. HUANG Gang, CHEN Chao. A coal-fired power plant 9000m2cooling tower construction overall stability analysis[J]. Journal of Special Structure, 2015, 32(6): 27−29.

[15] 李辉, 李龙华, 彭旭军. 双曲线冷却塔施工过程塔筒整体稳定分析[J]. 武汉大学学报工学版, 2012, 45(S1): 191−193. LI Hui, LI Longhua, PENG Xujun. Hyperbolic cooling tower construction process of the whole tower drum stability analysis[J]. Journal of Wuhan University of Technology, 2012, 45(S1): 191−193.

(编辑 伍锦花)

The influence of stiffening rings and meridian ribs on the wind-induced stable performance of super large cooling towers

KE Shitang, XU Lu, ZHU Peng

(Department of Civil Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

To study the influence of internal meridian rib and external stiffening ring on the wind-induced stable performance responses of super large cooling towers, a super large cooling tower under construction with the world’s highest height of 220 m in a domestic power plant was taken as an example. Four design schemes including smooth tower, meridian ribbed tower, stiffening ring tower, and meridian ribbed and stiffening ring tower were proposed. The overall stability, local stability and ultimate bearing capacity of cooling tower during construction were compared and analyzed considering the internal suction, construction load and concrete age. Then, the influence rule of stiffening ring and meridian rib setting on the wind induced stability of super large cooling tower was studied. The results show that setting stiffening ring improves the global stability of the structure by reducing wind-induced response, but it will significantly weaken the local stability of the structure. At the same time, setting radial on results in the decrease of structural overall stability and ultimate bearing capacity, but enhances the local stability of the structure. In addition, setting stiffening ring and meridian rib on the cooling tower significantly improves the whole, local buckling and construction whole process stability and ultimate bearing capacity of the cooling tower.

super large cooling tower; stiffening ring, meridian rib; ultimate bearing capacity

10.11817/j.issn.1672−7207.2018.02.022

TU279.7+41

A

1672−7207(2018)02−0422−09

2017−03−26；

2017−05−28

国家自然科学基金资助项目(51208254)；江苏省优秀青年基金资助项目(BK20160083)；博士后科学基金(2013M530255, 1202006B)；江苏高校‘青蓝工程’资助项目(2017)；江苏省六大人才高峰高层次人才计划项目(JZ-026)(Project(51208254) supported by the National Natural Science Foundation of China; Project(BK20160083) supported by the Outstanding Youth Fund of Jiangsu Province; Projects (2013M530255, 1202006B) supported by China Postdoctoral Science Foundation; Project(2017) supported by the Qing Lan Project in Jiangsu Province; Project(JZ-026) supported by the Six Talent Peaks Project in Jiangsu Province)

柯世堂，博士，副教授，从事结构工程与风洞试验研究；E-mail：keshitang@163.com