直排式真空预压法下竖井地基的非线性固结解析解

郭霄，谢康和，卢萌盟，邓岳保，黄廷



直排式真空预压法下竖井地基的非线性固结解析解

郭霄1, 2，谢康和1，卢萌盟3，邓岳保4，黄廷5

(1. 浙江大学 滨海和城市岩土工程研究中心，浙江 杭州，310058；2. 浙江省交通规划设计研究院，浙江 杭州，310006；3. 中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州，221116；4. 宁波大学 岩土工程研究所，浙江 宁波，315211；5. 浙江公路水运工程咨询公司，浙江 杭州，310004)

针对现有直排式真空预压法固结解未同时考虑土体非线性和逐渐加载这2个因素的不足，基于竖井内的真空负压沿深度方向呈线性分布的假设，同时考虑堆载引起的附加应力随时间的变化，采用非线性渗透和压缩模型，推导直排式真空预压法下竖井地基固结的通用解。在通用解的基础上，针对瞬间加载、线性加载和多级线性加载这3种特殊加载模式给出详解。研究结果表明：土体的渗透指数与压缩指数之比(c/k)、最终有效应力与初始有效应力之比以及堆载随时间的变化会对直排式真空预压法下的竖井地基固结度产生较大影响；当c/k＜1.0时，最终有效应力与初始有效应力之比越大，固结速率越快；当c/k＞1.0时，最终有效应力与初始有效应力之比越大，固结速率越慢；线性加载和分级线性加载可有效降低土体中的最大超静孔压；土体中的最终超静孔压为负压，在数值上与竖井内的真空负压相等。

直排式真空预压法；竖井；固结；土体非线性；解析解

真空预压法广泛用于机场跑道、高速公路、港口、码头等各类工程，是一种有效的软土地基加固方法[1]。真空预压法通常与竖井(目前主要为塑料排水板)结合使用。虽然早在20世纪50年代，国外研究者就已经提出真空预压法，但直到20世纪80年代末，随着高质量的塑料排水板和密封膜生产工艺的成熟，真空预压法才在世界范围内得到广泛应用。在国外，结合竖井的真空预压按其施工工艺的差别主要分为2大 类[2−3]：一类称为密封膜法，另一类称为真空井法或无密封膜法。CHAI等[4−6]介绍了真空井法的工作原理，总结其优点并在实际工程中进行了应用[4−6]。真空井法的主要特点是取消砂垫层，直接以覆土作为密封层，采用特制的接头把竖向塑料排水板与真空排水管网直接相连，因此，真空管产生的负压可直接作用于塑料排水板。国内对真空预压没有特别分类，大部分工程都采用密封膜和砂垫层，其实质与国外密封膜法一致，由于其应用广泛，国内也有研究将这类方法称为常规真空预压法[7]。近年来，直排式真空预压法逐渐被用于国内软土地基的处理，特别是在缺乏砂石材料的地区[7−10]。这种方法原理上与国外的真空井法或无密封膜法类似，下面统一称为直排式真空预压法。直排式真空预压法更多地应用于高含水率、高压缩性、高孔隙比淤泥土或吹填土地基的处理。目前，关于真空预压法固结的解析解研究主要针对常规真空预压法，如文献[11−12]中的解。常规真空预压法和直排式真空预压法主要区别在于：前者顶面(砂垫层)是透水性边界；后者的顶面是不透水边界，土体中的水只能通过塑料排水板与真空管接头处排出。而基于直排式真空预压法固结推导的解析解研究较少。CHAI等[4]针对直排式真空预压法的特点，假定单井顶面、底面为不透水层，且仅在真空管与竖井连接点给定真空负压的条件下，基于HANSBO单井理论[13]的假设和思路，得出了超静孔压解。但HANSBO理论[13]基于堆载预压模型，未考虑真空预压下竖井内的真空负压随深度的衰减。INDRARATNA等[14−15]的研究表明，直排式真空预压下竖井内的真空负压会在较短时间内达到稳定态，即对于直排式真空预压法，可假设真空负压沿深度方向线性衰减。GENG等[3]针对常规真空预压和点排式真空预压的不同特点，同时考虑堆载随时间的变化，得出相应的解析解，并对这2类真空预压进行了对比研究，但其解析解需采用傅里叶逆变换求解，较难在实际工程中应用。以上解析解均假设土体的渗透系数和压缩模量为常数。但事实上，土体是非线性的，土的渗透系数、孔隙比和有效应力存在非线性关系。RAYMOND等[16−19]指出，−lg渗透模型对于常见的软黏土都是普遍适用的，其表达式为=0+klg(/0)(其中，k为渗透指数，0和0分别为初始孔隙比和初始渗透系数，和分别为任一时刻土的孔隙比和渗透系数)。MESRI等[20]进一步指出−lg渗透模型的优点在于：考虑土体初始状态0和0，同时渗透指数k易于测定，对天然软黏土具有较好的代表性。有关渗透指数k的测定方法见文献[21]。

土的非线性压缩特性对土的固结变形性状有重要的影响。−lg压缩模型是目前最为常用的软黏土非线性压缩模型，其表示式为=0+clg(/0)(其中，c为压缩指数，0和分别为土体初始有效应力和任一时刻有效应力)。由于直排式真空预压法多应用于高含水率、高压缩性、高孔隙比的淤泥土或吹填土，假设渗透系数和压缩模量为常数，在实际过程中会产生较大的误差。综上所述，虽然直排式真空预压固结的解析解研究已取得一定进展，但均未同时考虑土体非线性和逐渐加载的影响。为此，本文作者假设竖井内的真空负压沿深度方向呈线性分布，同时考虑堆载引起的附加应力随时间的变化，并采用孔隙比和有效应力、渗透系数之间的半对数线性关系，推导出适应于直排式真空预压法固结的通用解析解。在此基础上，进一步详细给出瞬时加载、线性加载和多级线性加载3种特殊加载模式下的解。最后，对直排式真空预压下固结特性参数进行分析。

1 固结基本方程及求解

图1所示为直排式真空预压法固结的计算简图。其中：为竖井计算长度，即软土层厚度；h为地基水平向渗透系数；s为竖井周围涂抹区的水平向渗透系数；w为竖井渗透系数；s为涂抹区半径；w为竖井半径；e为竖井影响区半径；()为随时间变化的顶面堆载；和分别为径向及竖向坐标；−v()为真空负压在竖井中沿深度的传递函数。根据直排式真空预压特点，竖井地基顶面和底面考虑为不透水边界，因此，直排式真空预压时不发生竖向渗流，仅发生径向渗流。主要假设如下。

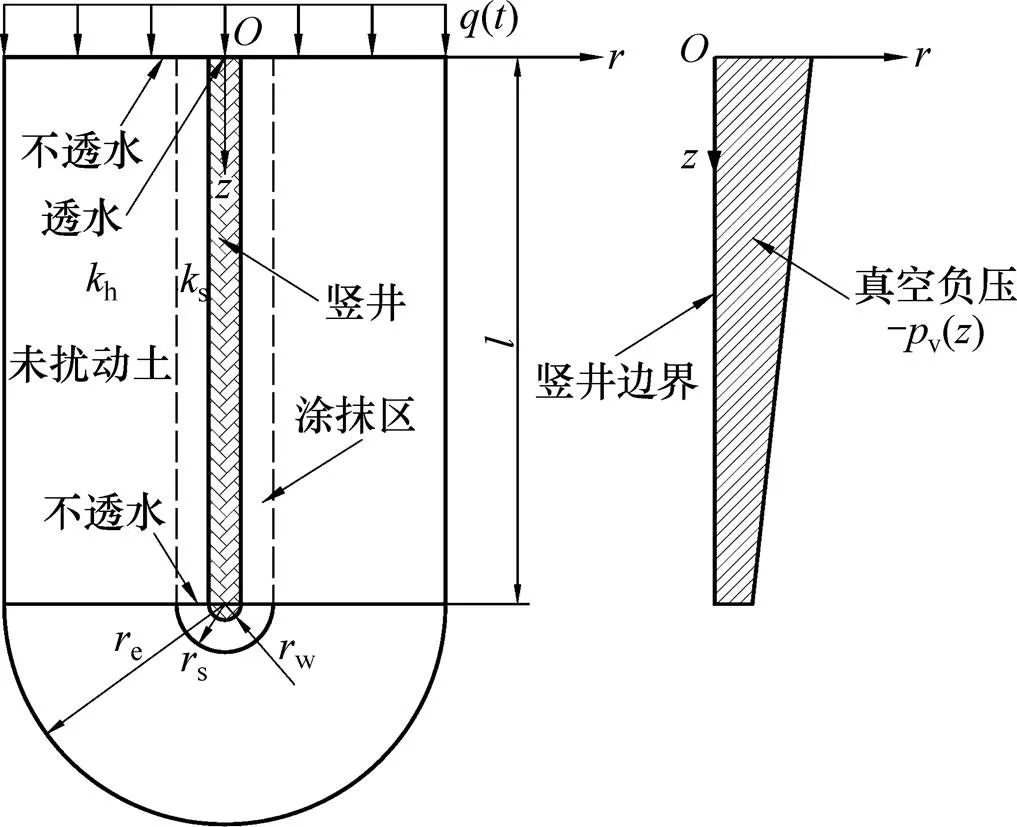
图1 直排式真空预压法竖井地基固结计算简图

1) 等应变条件成立[22]。即竖井影响区范围内同一水平面上各点的竖向变形是相等的。

3) 真空负压瞬时施加。在实际工程中大多假设−v()分布沿竖井深度方向线性衰减(见图1)。

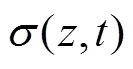
其余假设与文献[22]和[23]中的相同。

等应变径向固结方程如下：

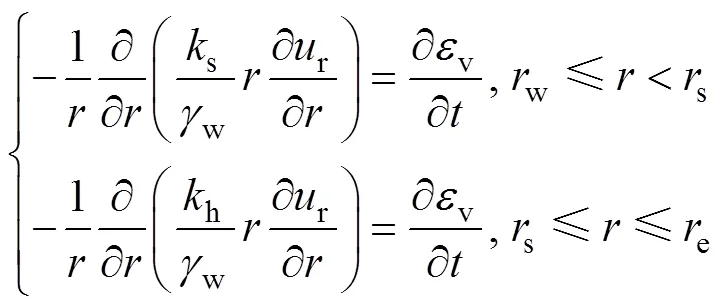
其中：r为影响区土体内任一点的(超静)孔压；v为影响区内任一点的体积应变(与垂直应变相等)；w为水的重度；为时间。

式(4)的边界条件和初始条件如下：

根据文献[23]中的推导思路，对式(2)进行积分并结合边界条件1)~2)可得：

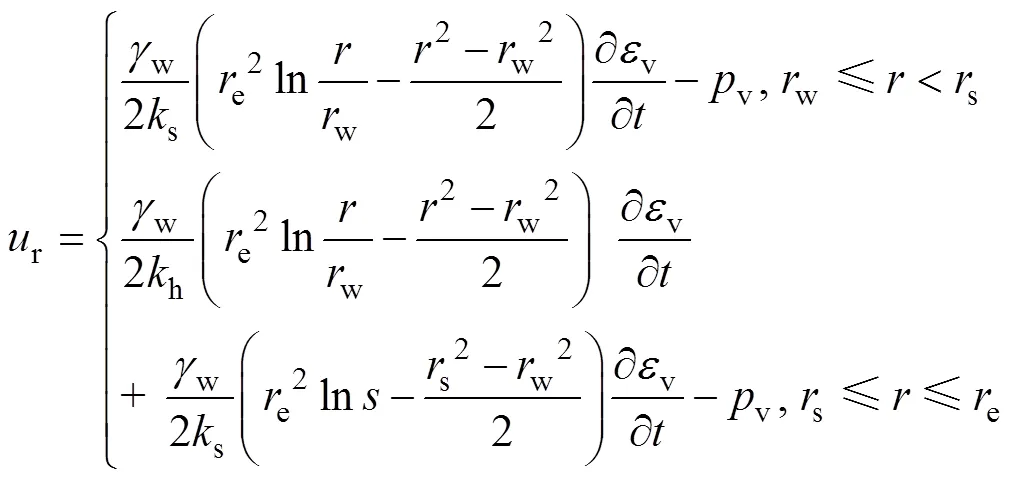
式中：sw。

任一深度平均孔压可表示为

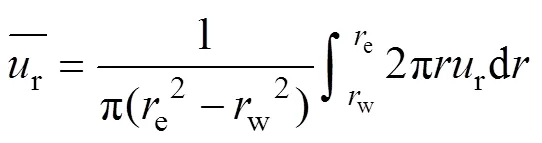
将式(3)代入式(4)，积分后得

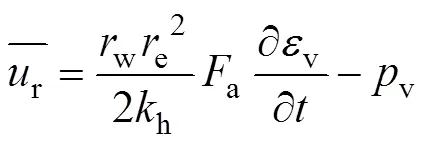
式中：

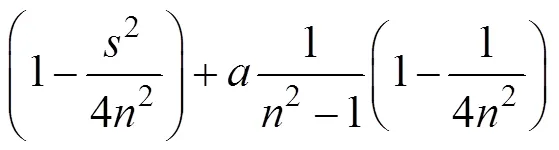
为井径比，ew；hs，假设其值在固结过程中不变。

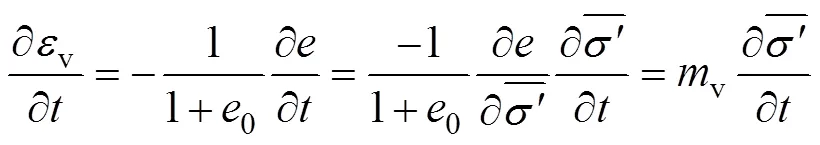
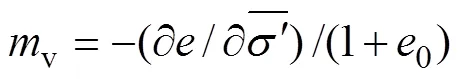
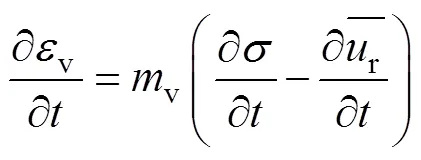
将式(7)代入式(5)可得

根据式(1)，土的固结系数h和初始固结系数h0可表示为

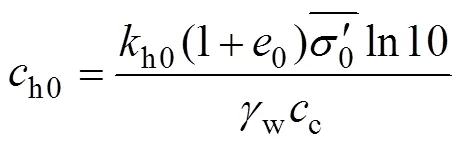
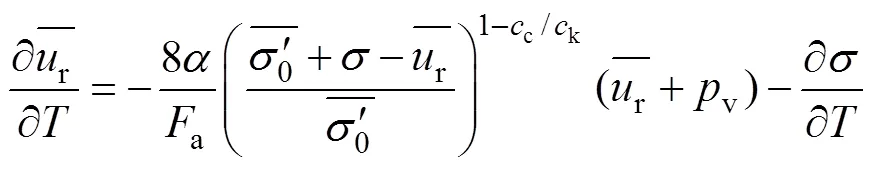
式中：可表示为

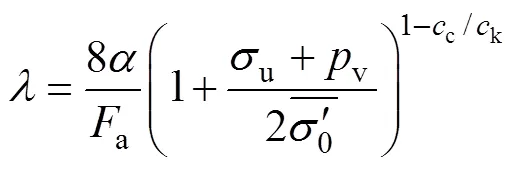
式(12)为常系数一阶线性微分方程，其通解为

其中为待定常数。结合初始条件3)，式(14)可表 示为

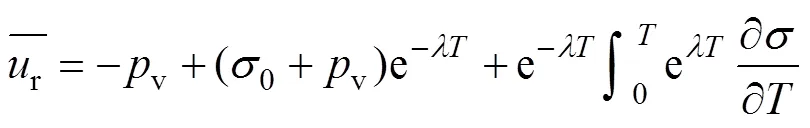
按应力定义的总平均固结度r可表示为

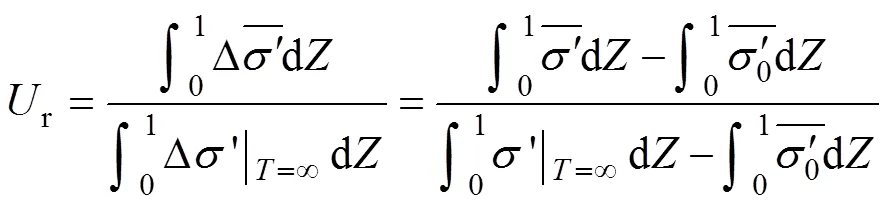
根据有效应力原理并将式(17)代入式(16)可得

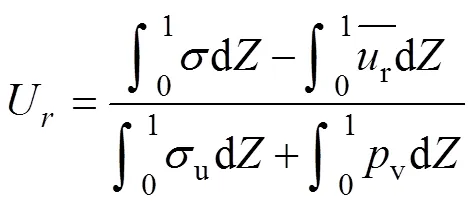
按应变定义的总平均固结度s可表示为

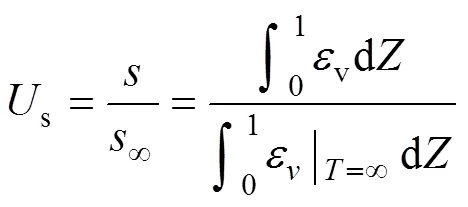
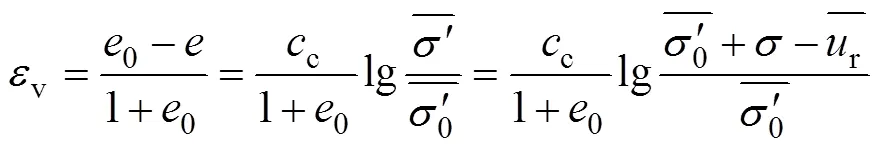
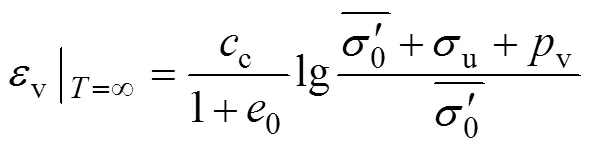
将式(20)~(21)代入式(19)，可得

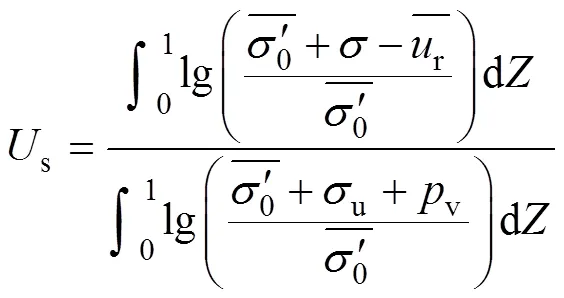
式(15)，(18)和(22)即为直排式真空预压法固结的通用解析解。

2 3种特殊加载情况下的平均孔压解

2.1 瞬时加载

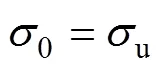
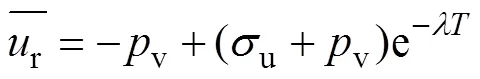
2.2 单级线性加载

单级线性加载是常见的加载方式，通常假设其引起的附加应力也是单级线性增加，如图2(b)所示。其表达式如下：

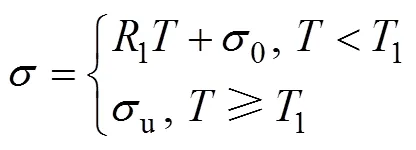
将式(24)代入式(15)，可求出在真空预压下附加应力单级线性增加的平均超静孔压解，即

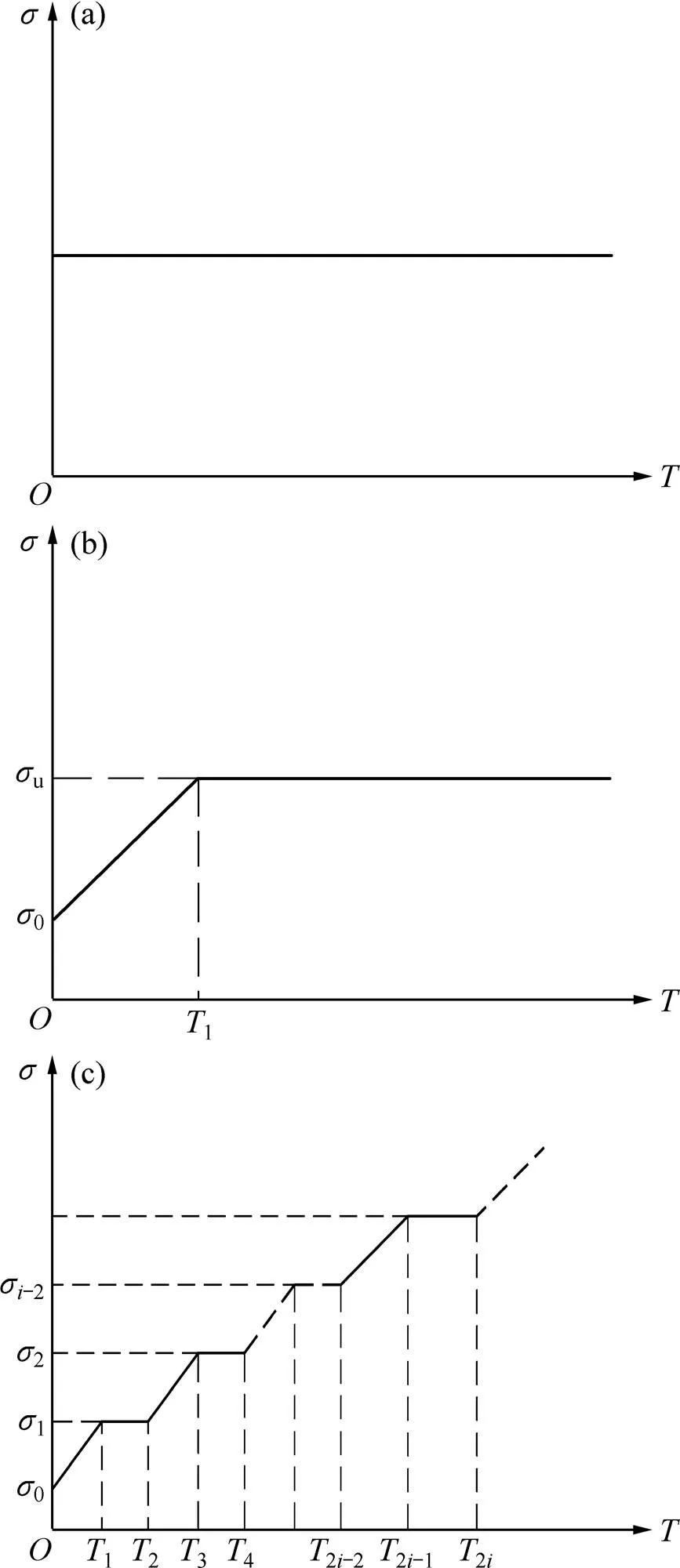
(a) 瞬时加载；(b) 单级线性加载；(c) 多级线性加载

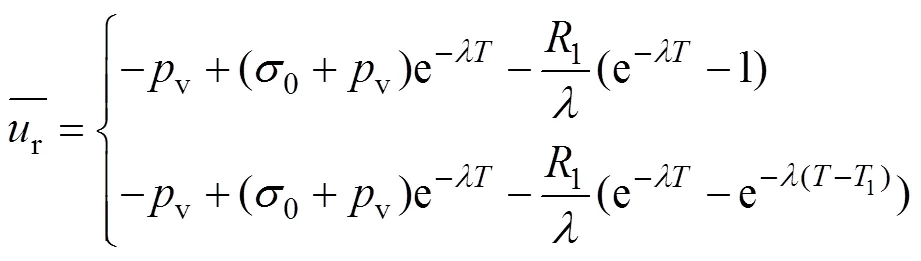
2.3 多级线性加载

由于直排式真空预压法常应用于含水量大、初始固结程度低的吹填土，一次性堆载易发生失稳，因此，在实际施工中常使用逐级堆载方式，等到土体有效应力增加到一定程度后，再加载下一级。在这种情况下，同样可以假设其引起的附加应力也是逐级线性增加，如图2(c)所示，应力表达式如下：

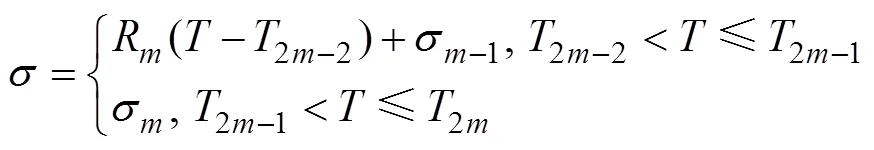
将式(28)代入式(17)，可求出在真空预压下附加应力多级线性增加的超静孔压解，即

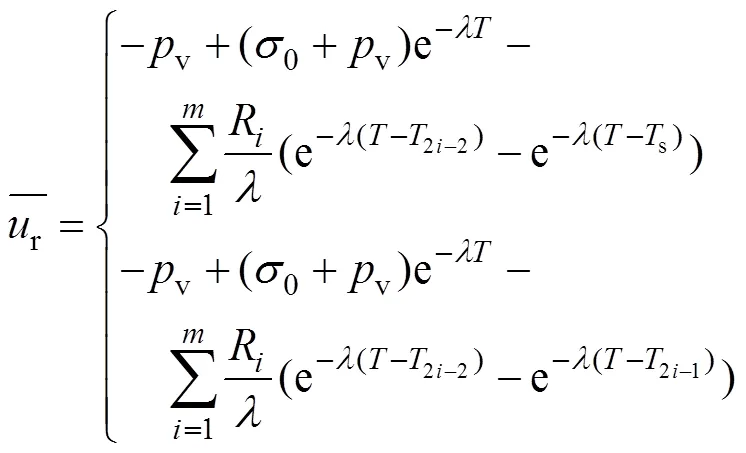
3 固结计算及分析

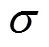
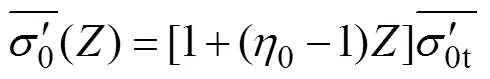
附加应力分布函数可表示为

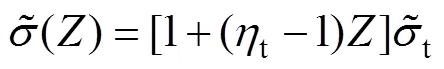
(a) 真空负压分布；(b) 初始有效应力分布；(c) 附加应力分布

图3 真空负压、平均初始有效应力和附加应力沿土体深度分布

Fig. 3 Variation of vacuum pressure, average effective stress and additional stress in soil along depth

图4所示为真空负压、堆载历时对土体固结度的影响。从图4可以看出：在瞬时加载情况下，真空负压对固结速率几乎无影响。当在线性加载，且在加载历时相同的情况下，真空负压越大，土体的固结速率越快。

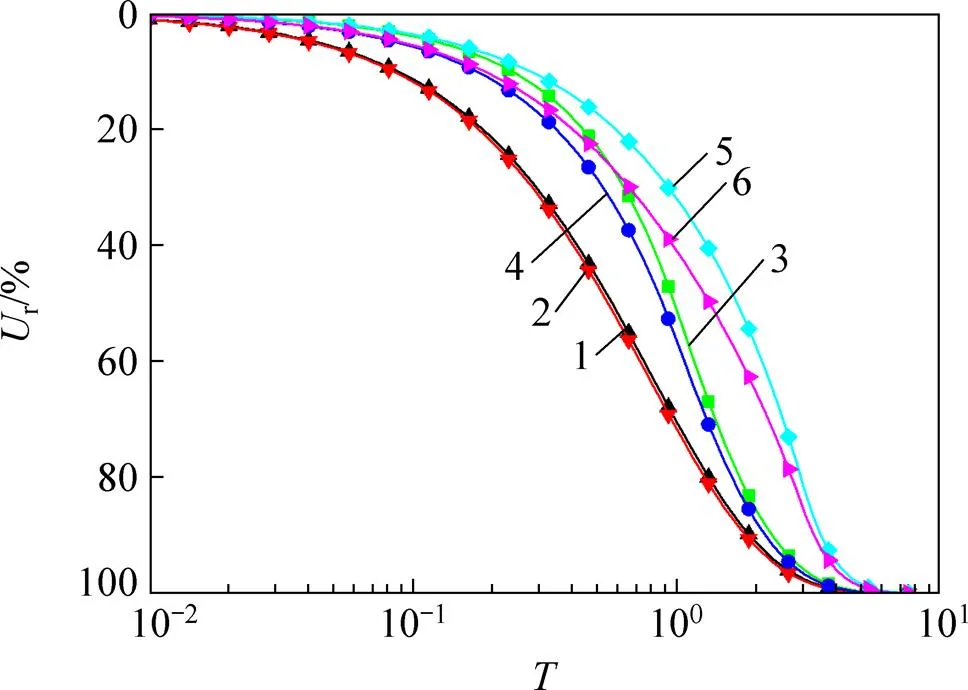
ηv=0.5；=50；η0=2；n=15；s=5；kh/ks=5；cc/ck=0.75

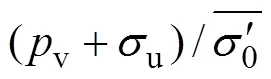
n=15；s=5；kh/ks=5；cc/ck=0.5；pvt=50；ηv=1.0；σut=150；ηt=1.0 ：1—4.0；2—2.0；3—1.0；4—0.5。

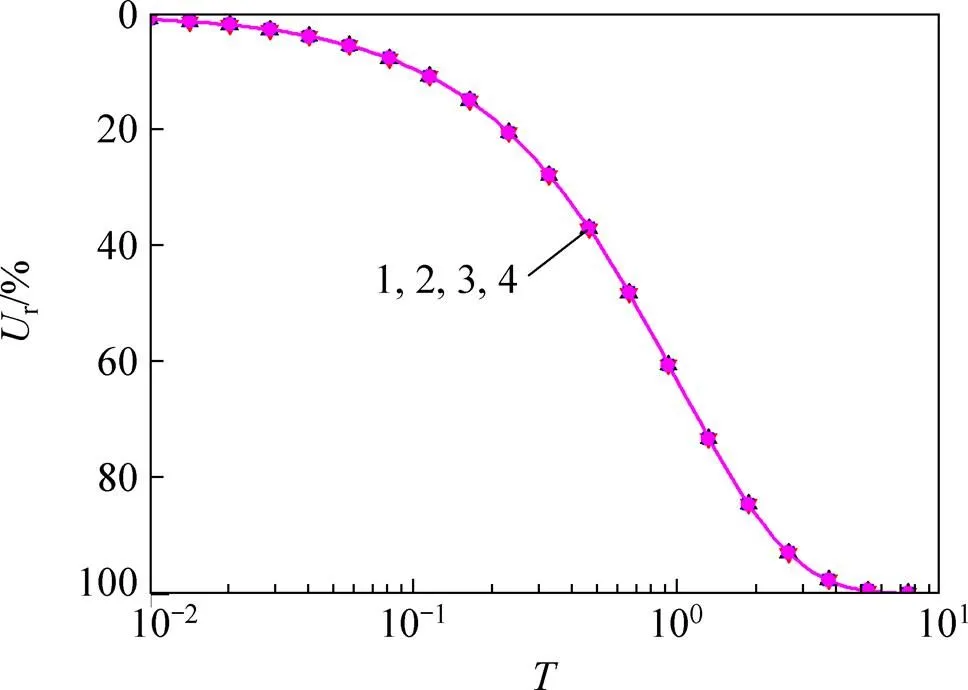
n=15；s=5；kh/ks=5；cc/ck=1.0；pvt=50；ηv=1.0；σut=150；ηt=1.0 ：1—4.0；2—2.0；3—1.0；4—0.5。

图6所示为当c/k=1.0时，最终有效应力与初始有效应力之比与平均固结度的关系。从图6可以看出：当c/k=1.0时，最终有效应力与初始有效应力之比对固结速率无影响。这一点从式(13)可以得到验证。

图7所示为当c/k=2.0时，最终有效应力与初始有效应力之比与平均固结度的关系。从图7可以看出：当c/k=2.0时，最终有效应力与初始有效应力之比越大，固结速率越慢。

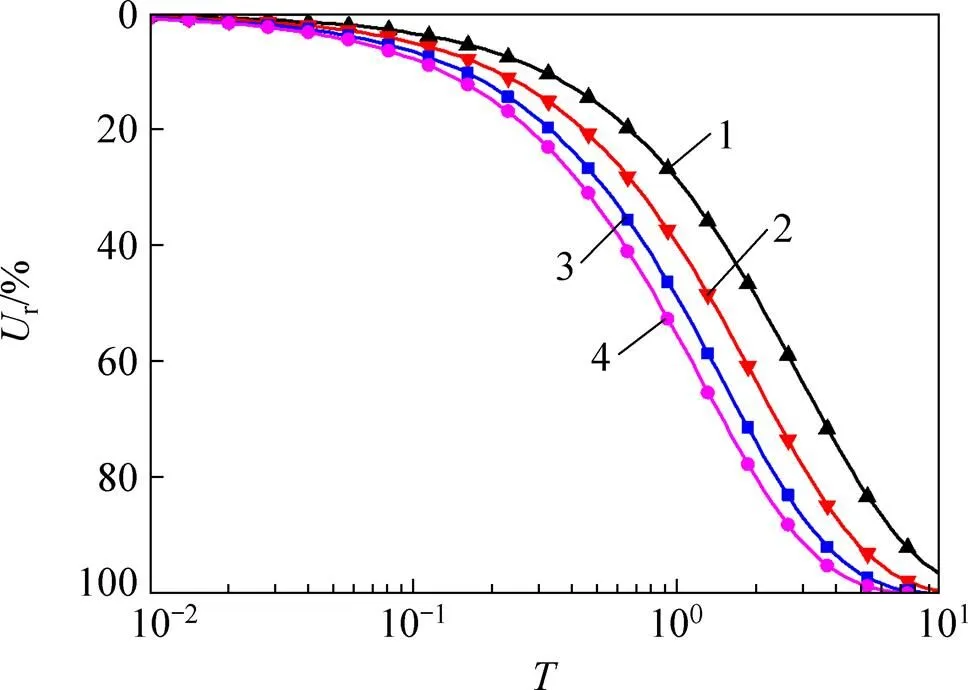
n=15；s=5；kh/ks=5；cc/ck=2.0；pvt=50；ηv=1.0；σut=150；ηt=1.0 ：1—4.0；2—2.0；3—1.0；4—0.5。

从图5~7可以看出：当c/k＜1.0时，最终有效应力与初始有效应力之比越大则固结速率越快；当c/k＞1.0时，最终有效应力与初始有效应力之比越大，固结速率反而越慢。因此，除土体的固结系数外，c/k对土体的固结有着重要的影响。

图8所示为二级线性加载下参数c/k对固结度的影响。从图8可以看出：c/k越大，固结的速率越慢。

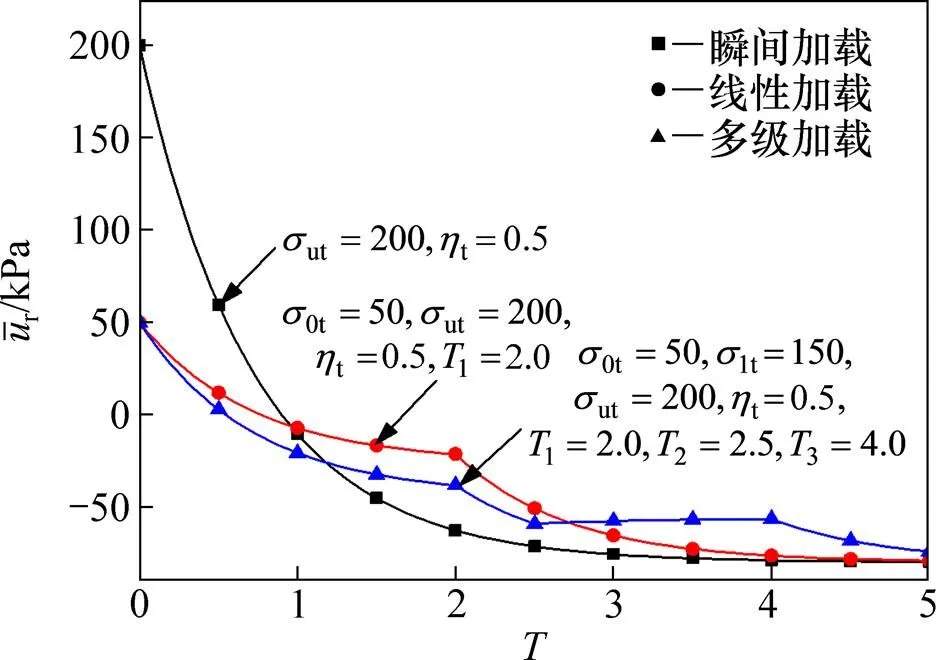
图9所示为3种加载模式下，=处的平均超静孔压随时间的变化。从图9可以看出：在最终附加应力相同的情况下，瞬时加载时土体中将产生最大的超静孔压，而线性加载或多级线性加载可有效减小固结过程中超静孔压。在真空预压下最终土体中的超静孔压为负，数值上等于竖井内的真空负压。真空预压结合合理的堆载时序，可减小最大超静孔压，提高处理过程中地基的稳定性。

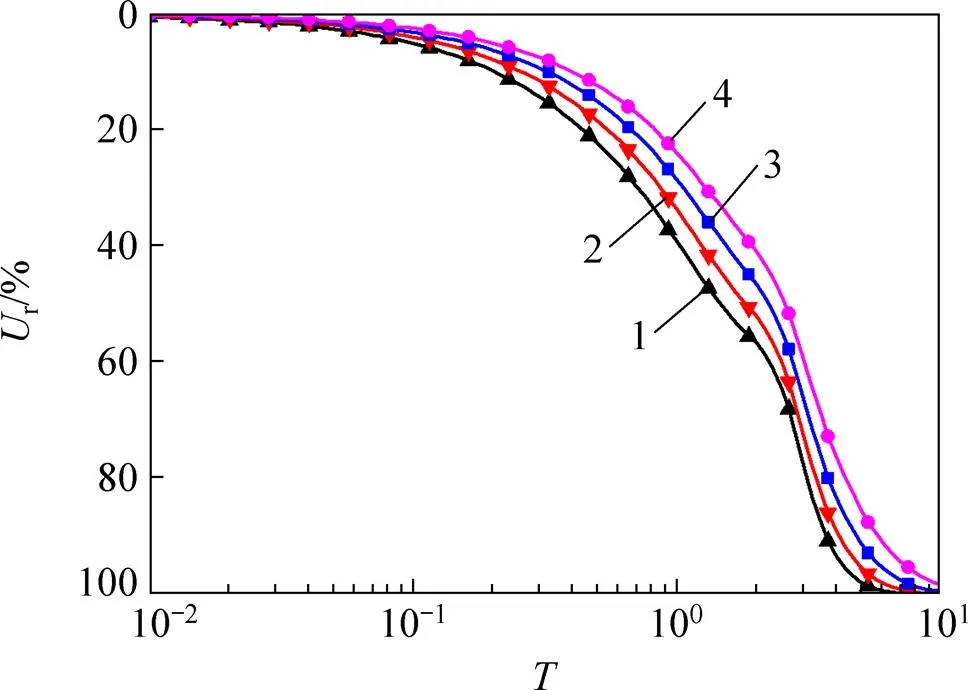
n=15；s=5；kh/ks=5；pvt=50；ηv=0.5；σ0t=40；σ1t=100；σut=200；T1=1；T2=2；T3=3；ηt=0.5；=50；η0=0.5 cc/ck：1—0.5；2—1.0；3—1.5；4—2.0。

pv=80，ηv=1/2，=50，η0=2.0，n=15，s=5，kh/ks=5，Z=Z/l=0

4 结论

1) 建立同时考虑土体非线性和逐渐加载的直排式真空预压法固结方法。

2) 在瞬时加载情况下，真空负压对固结速率几乎无影响。在线性加载，加载历时相同的情况下，真空负压越大，土体的固结速率越快。

3) 当c/k＜1.0时，最终有效应力与初始有效应力之比越大，固结速率越快；当c/k＞1.0，最终有效应力与初始有效应力之比越大，固结速率反而越慢。在其他参数一致的情况下，c/k越大，则固结速率 越慢。

4) 采用瞬时加载，土体中将产生较大的超静孔压，而线性加载或多级线性加载可有效减小固结过程中的超静孔压。在真空预压下，最终土体中的超静孔压为负，数值上等于竖井内的真空负压。

[1] INDRARATNA B. Recent advances in the application of vertical drains and vacuum preloading in soft soil stabilization[J]. Australian Geomechanics Society, 2010, 45(2): 1−43.

[2] CHAI J C, CARTER J P, LIU M D. Methods of vacuum consolidation and their deformation analyses[J]. Proceedings of the Institution of Civil Engineers Ground Improvement, 2013, 166(1): 35−46.

[3] GENG X Y, INDRARATNA B, RUJIKIATKAMJORN C. Analytical solutions for a single vertical drain with vacuum and time-dependent surcharge preloading in membrane and membraneless systems[J]. International Journal of Geomechanics, 2012, 12(1): 27−42.

[4] CHAI J C, CARTER J P. Deformation analysis in soft ground improvement[M]. Springer, 2011: 1−247.

[5] CHAI J C, MIURA N, BERGADO D T. Preloading clayey deposit by vacuum pressure with cap-drain: analyses versus performance[J]. Geotextiles and Geomembranes, 2008, 26(3): 22−230.

[6] CHAI J C, HONG Z S, SHEN S L. Vacuum-drain consolidation induced pressure distribution and ground deformation[J]. Geotextiles and Geomembranes, 2010, 28(3): 525−535.

[7] 夏玉斌, 陈允进. 直排式真空预压法加固软土地基的试验与研究[J]. 工程地质学报, 2010, 18(3): 376−384. XIA Yubin, CHEN Yunjin. Experimental study and research on straight-line vacuum preloading method to reinforce soft soil[J]. Journal of Engineering Geology, 2010, 18(3): 376−384.

[8] 夏玉斌, 陈健, 陈允进. 直排式真空预压软基加固效果及经济性分析[J]. 水运工程, 2011(9): 224−229. XIA Yubin, CHEN Jian, CHEN Yunjin. Effect and economic analysis of direct vacuum preloading method for consolidation of soft ground[J]. Port & Waterway Engineering, 2011(9): 224−229.

[9] 王旭, 刘强, 芦志强. 直排式真空预压工艺创新实践[J]. 水运工程, 2014(4): 164−167. WANG Xu, LIU Qiang, LU Zhiqiang. Innovative practice of straight-line vacuum preloading[J]. Port & Waterway Engineering, 2014(4): 164−167.

[10] 王军, 蔡袁强, 苻洪涛，等. 新型防淤堵真空预压法室内与现场试验研究[J]. 岩石力学与工程学报, 2014, 33(6): 1257−1268. WANG Jun, CAI Yuanqiang, FU Hongtao, et al. Indoor and field experiment on vacuum preloading with new anti-clogging measures[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(6): 1257−1268.

[11] 董志良. 堆载及真空预压砂井地基固结解析理论[J]. 水运工程, 1992(9): 1−7. DONG Zhiliang. Analytical consolidation theory of sand drain ground under preloading with vacuum preloading[J]. Port and Waterway Engineering, 1992(9): 1−7.

[12] 彭劼, 董江平, 宋恩润, 等. 考虑加载过程的真空预压轴对称解析解[J]. 岩土力学, 2010, 31(S1): 79−85. PENG Jie, DONG Jiangping, SONG Enrun, et al. Axisymmetric analytical solution of vacuum preload considering the loading process[J]. Rock and Soil Mechanics, 2010, 31(S1): 79−85.

[13] HANSBO S. Consolidation of fine-grained soils by prefabricated drains[C]//Proceedings of 10th International Conference on Soil Mechanics and Foundation Engineering. Rotterdam, Netherlands: August Aimé Balkema, 1981: 677−682.

[14] INDRARATNA B, RUJIKIATKAMJORN C, AMERATUNGA J, et al. Performance and prediction of vacuum combined surcharge consolidation at port of Brisbane[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(11): 1007−1018.

[15] INDRARATNA B, SATHANANTHAN I, RUJIKIATKAMJIORN C, et al. Analytical and numerical modeling of soft soil stabilized by prefabricated vertical drains incorporating vacuum preloading[J]. International Journal of Geomechanics 2005, 5(2): 114−124.

[16] RAYMOND G P. Laboratory consolidation of some normally consolidated soil[J]. Canadian Geotechnical Journal, 1966, 4(4): 217−234.

[17] MESRI G, ROKHASR A. Theory of consolidation for clays[J]. Clay and Clay Mineral, 1974, 19(3): 151−158.

[18] BALASUBRAMANIAM A S, CHOWDARY A R. Deformation and strength characteristics of soft Bangkok clay[J]. Journal of Geotechnical Division, ASCE, 1978, 104(9): 1153−1167.

[19] 谢康和, 庄迎春, 李西斌. 萧山饱和软粘土的渗透性试验研究[J]. 岩土工程学报, 2005, 27(5): 591−594. XIE Kanghe, ZHUANG Yingchun, LI Xibin. Laboratory investigation of permeability characteristics of Xiaoshan clay[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(5): 591−594.

[20] MESR G, TAVENAS F. Discussion: Permeability and consolidation of normally consolidated soils[J]. Journal of Geotechnical Engineering, ASCE, 1983, 109(6): 873−878.

[21] 齐添. 软土一维非线性固结理论与试验对比研究[D]. 杭州: 浙江大学建筑工程学院, 2008: 9−15. QI Tian. Theoretical and experimental studies on one-dimensional nonlinear consolidation of soft soil[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2008: 9−15.

[22] BARRON R A. Consolidation of fine-grained soils by drain wells[J]. Transaction of the American Society of Civil Engineers, 1948, 113: 718−754.

[23] 谢康和, 曾国熙. 等应变条件下的砂井地基固结解析理论[J]. 岩土工程学报, 1989, 11(2): 3−17. XIE Kanghe, ZENG Guoxi. Consolidation theories for drain walls under equal strain condition[J]. Chinese Journal of Geotechnical Engineering, 1989, 11(2): 3−17.

[24] LU M M, WANG S Y, SLOAN S W, et al. Nonlinear radial consolidation of vertical drains under a general time-variable loading[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(1): 51−62.

(编辑 伍锦花)

Nonlinear analytical solution for consolidation of vertical drains by straight-line vacuum preloading method

GUO Xiao1, 2, XIE Kanghe1, LU Mengmeng3, DENG Yuebao4, HUANG Ting5

(1. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;2. Zhejiang Provincial Plan Design and Research Institute of Communications, Hangzhou 310006, China;3. State Key Laboratory for Geomechanics and Deep Underground Engineering,China University of Mining and Technology, Xuzhou 221116, China; 4. Institute of Geotechnical Engineering, Ningbo University, Ningbo 315211, China; 5. Zhejiang Highway & Water Transportation Engineering Consulting Corporation, Hangzhou 310004, China)

Considering that current analytical solutions for straight-line vacuum preloading method do not take the nonlinear property of soil and the time-dependent loading into account simultaneously, a general analytical solution was proposed. The solution was based on the assumption that the vacuum pressure distributes linearly along the depth of vertical drains, and additional stress caused by a general time-dependent loading was also considered. Detailed solutions were studied for three special loading schemes, i.e. instantaneous loading, ramp loading and multi-stage loading. The results show that consolidation degree is significantly affected by the variational ratio of compressibility index to permeability index(c/k), the ratio of ultimate effective stress to initial effective stress, and the loading time. When the ratio ofc/kis less than 1.0, a high ratio of the ultimate effective stress to the initial effective stress leads to a rapid consolidation rate. However, when ratio of indicesc/kis higher than 1.0, the case is reversed. In addition, the maximum induced excess pore water pressure can be reduced by applying the load in stages. At the end of consolidation, a negative excess pore water pressure occurs, the value of which equals to vacuum pressure in vertical drain.

straight-line vacuum preloading method; vertical drains; consolidation; nonlinear property of soil; analytical solution

10.11817/j.issn.1672−7207.2018.02.017

TU375.4

A

1672−7207(2018)02−0384−09

2017−03−02；

2017−05−06

国家自然科学基金资助项目(51179170，51278453，51308309)(Projects(51179170, 51278453, 51308309) supported by the National Natural Science Foundation of China)

谢康和，教授，博士生导师，从事岩土工程研究；E-mail：Zdkhxie@Zju.edu.cn