不同伴随流条件下的集束射流流场特性

赵飞，孙冬柏，朱荣，杨凌志



不同伴随流条件下的集束射流流场特性

赵飞1，孙冬柏1，朱荣2，杨凌志3

(1. 北京科技大学 国家材料服役安全科学中心，北京，100083；2. 北京科技大学 冶金与生态工程学院，北京，100083；3.中南大学 资源加工与生物工程学院，湖南 长沙，410083)

针对不同伴随流参数条件下的集束射流和普通超音速射流流场特性进行数值模拟和试验研究。研究结果表明：伴随流气体影响喷管出口温度和压力，导致超音速主射流速度和温度出现重复波动；高温、大流量伴随流气体形成的低密度和高速环境可保护超音速射流，降低射流径向的扩展率和轴向速度的衰减速率；伴随流气体温度越高，流量越大，射流速度和温度核心段长度越长。与普通超音速射流相比，伴随流气体改变射流半速度宽度和涡量的分布；伴随流温度越高，流量越大，射流在更长的距离内保持较低的湍流强度。

伴随流；超音速射流；流场特性

超音速氧气射流广泛应用于转炉和电弧炉炼钢。高速氧气射流进入熔池中与钢液发生化学反应，通过气流对熔池的搅拌作用而加速冶炼过程。考虑到氧气射流的冲击深度，超音速射流马赫数一般为2.0左 右[1−2]。超音速射流在运动过程中会卷吸周围环境气体，导致射流沿径向直径的扩展和轴向速度的衰减，减少射流对熔池的冲击力[3−4]。集束射流技术可降低射流动量的损失并延长射流核心段的长度[5]。集束射流技术的原理是在普通超音速射流的基础上环绕火焰，利用火焰的封套作用减少超音速射流对周围环境气体的卷吸，抑制超音速射流速度的衰减。多年来，MAHONEY等[6−7]对集束射流特性进行了广泛的研究：LIU等[8]研究了CH4作为伴随流气体条件下集束射流对金属熔池的搅拌力；MEIDANI等[9]通过水模试验研究了伴随压缩空气条件下的超音速射流；ALAM等[10]模拟计算并对比了有无环绕气体和火焰条件下普通射流和集束射流特性；LIU等[11]通过模拟和试验研究了不同环境温度和主氧温度条件下集束射流流场特性。上述研究主要针对不同伴随流燃料和氧气流量条件下的集束射流流场特性，但无法表征具体伴随流参数对超音速射流流场特性的影响。最近，ODENTHAL等[12]提出了利用高温气体代替火焰包裹形成集束射流的方法，并对此进行了模拟研究。本文作者针对不同温度和流量的伴随气体，从射流轴线速度、静温、涡量和湍流强度等方面研究高温高速伴随气体温度和流量对集束射流流场特性的影响。

1 试验装置和数值模拟

1.1 试验装置

集束射流试验装置如图1所示。Laval喷管产生不同伴随流参数条件的超音速射流，喷管出口设计马赫数为2.1，流量为0.2 kg/s，喉口和出口直径分别为10.85 mm和14.70 mm。利用固定在夹具上的皮托管和热电偶测量射流的压力和温度，通过夹具的前后移动测量轴线不同位置上主射流的参数。

图1 试验装置图

射流速度、压力和温度的关系如下[13]：

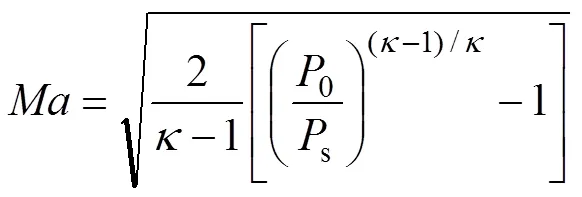
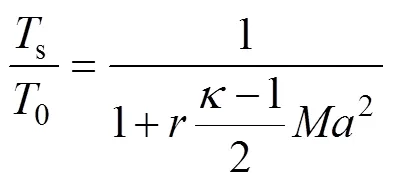
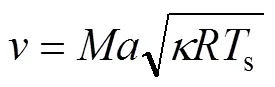
式中：0和0分别为测量得到的射流总压力和总温度；s为测量得到的射流静压；s为射流静温；和分别为射流马赫数和速度；为气体比热容比；为气体常数；为气体恢复系数，即气体动能实际转化为热能的比例。

1.2 数值模拟

基于雷诺平均N-S方程[14]，连续性、动量和能量方程如下[15]：

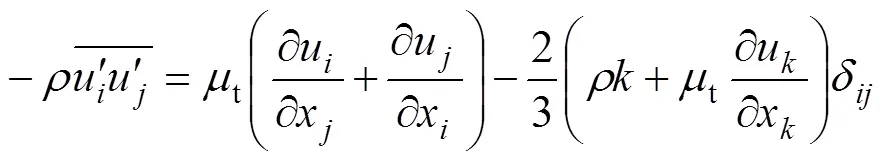
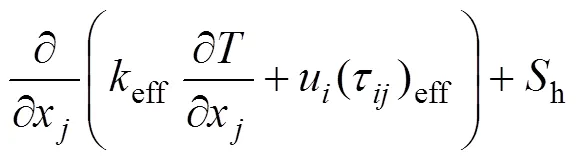
本研究选用的湍流模型为SST−模型[16]，是由Menter提出的双方程模型，在射流远场使用自由射流的−模型，近壁面采用−模型[17−19]，其输运方程如下：

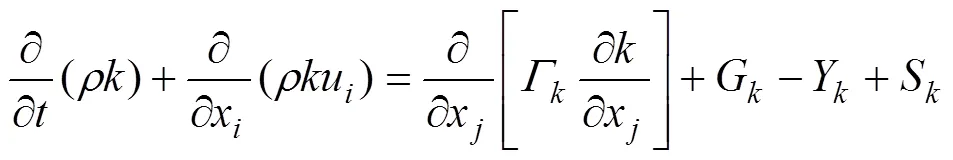
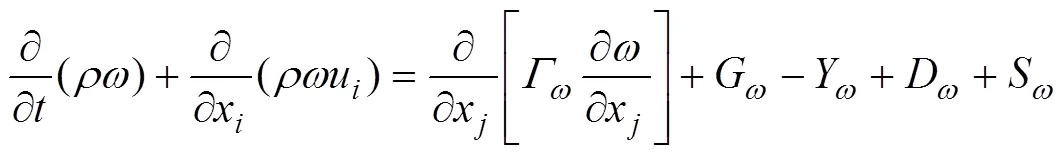
表1 边界条件

式中：为流体密度；t为湍流黏度；u为速度在方向上分量；G为由平均速度梯度而产生的湍流动能；G为由耗散率产生的湍流动能；Y和Y分别为由于湍流而引起的和的耗散；Г和Г分别为和的有效扩散率；D为阻尼交叉扩散项；S和S分别自定义源相。

1.3 边界条件

数值模拟使用的计算域和边界条件如图2所示。计算域包括Laval喷管、伴随流喷管和射流扩展区域。Laval喷管和伴随流喷管入口边界条件为压力入口边界条件，射流扩展区域为压力出口边界条件，长度为102e(e为喷管出口直径)，宽度为20e。考虑到计算精度和边界条件的合理性，整个流体计算域采用三维几何模型，并选用COUPLE算法和二阶迎风格式提高计算精确度。具体边界条件如表1所示。

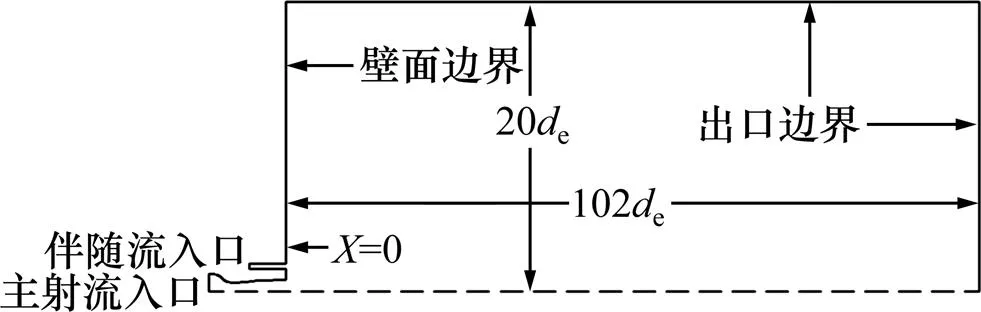
图2 计算域和边界条件

1.4 网格无关性验证

计算网格划分的质量会直接影响计算结果的精确性。网格质量越好，计算结果越准确，但同时也会导致计算成本的增加，因此，计算网格的划分要综合考虑计算结果准确性和计算时间。本文分别在无伴随流条件下对3种不同精度的网格进行计算。不同精度网格划分条件下射流速度沿轴向的分布情况如图3所示。其中低密度网格的总数为85 300个，中密度网格数量为195 000个，高密度网格数量为262 000个。采用中密度网格与低密度网格计算得到的射流速度分布差值约为8%，而中密度网格与高密度网格计算的结果相差无几。因此，选用中密度网格作为计算网格，在保证计算结果精度的同时可缩短计算时间。

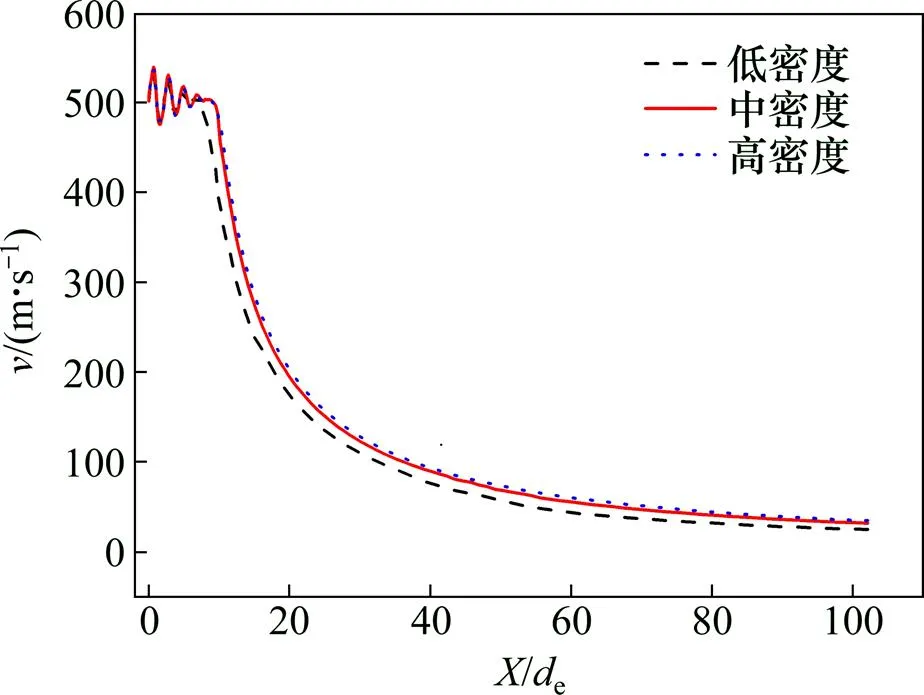
图3 不同精度网格条件下射流轴线速度

2 结果与讨论

2.1 轴线速度分布

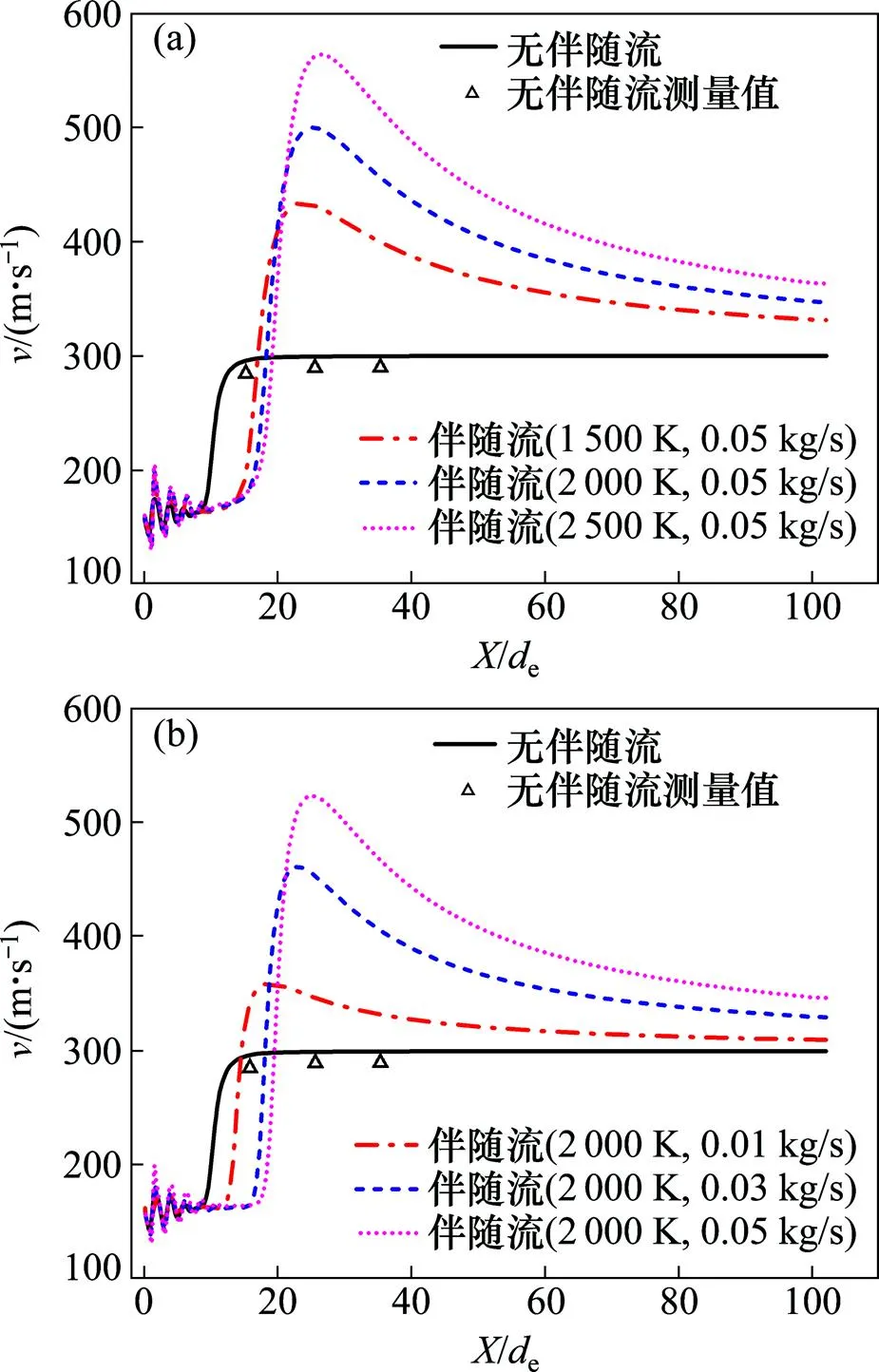
不同伴随流温度和流量条件下集束射流速度沿轴线分布趋势如图4所示。射流在离开喷管出口之后，速度出现重复波动，随后射流速度沿轴线不断减小。在不同温度伴随流条件下，喷管出口速度波动程度基本相同，但强度均高于无伴随流条件下的速度波动强度。无伴随流条件下的射流速度波动是喷管实际尺寸与理论设计尺寸的误差导致的，但在环绕伴随流之后，喷管出口压力和温度受到伴随流的影响，从而导致射流波动加剧。从图4(a)可以看出：集束射流条件下射流轴线速度的衰减迟于普通超音速射流轴线速度的衰减。普通超音速射流在距离喷管出口平面10e处开始衰减，而在环绕伴随气体温度分别为1 500，2 000和2 500 K的条件下，射流速度开始衰减的位置分别延长至15e，16e和17e。随着伴随流气体温度升高，射流速度核心段变长。伴随流气体温度越高，气体密度越低，超音速主射流对伴随气体的卷吸量减少。因此，高温伴随气体条件下超音速射流轴线速度的衰减迟于普通超音速射流的衰减。

从图4(b)可以看出：在不同伴随流流量条件下，射流在离开喷管出口之后，速度同样出现重复波动；随着伴随气体流量增大，一方面，射流速度波动变强，振幅变大；另一方面，射流稳定段变长，速度衰减缓慢；伴随流流量越大，速度越快，伴随流与超音速主射流的速度差越小，伴随流对超音速流卷吸过程的阻碍作用减弱。数值模拟结果和试验结果吻合度较高，二者平均差值约为5%。产生这种差异的部分原因是模拟过程中所涉及的不确定因素，包括湍流模型的选择和计算网格的划分。但总体来说，这种不确定性产生的差异低于数值模拟结果与试验结果的差异。

(a) 不同温度伴随流；(b) 不同流量伴随流

图5所示为不同伴随流温度和流量条件下射流半速度宽度(1/2)的分布趋势。射流半速度宽度是指射流在其横截面上速度达到轴线速度一半时对应的宽度。从图5(a)可以看出：不同伴随流条件下的半速度宽度的分布趋势是相同的，但在射流离开喷管出口的初始阶段有很大不同。普通超音速射流的半速度宽度的变化分为2个阶段：首先从喷管出口缓慢增加直至10e，随后以较高速率增长。而集束射流条件下射流的半速度宽度变化分为3个阶段：1) 从离开喷管出口后快速增长，伴随流温度越高，增加速率越快。这是因为环绕的高温气体在超音速射流周围形成低密度区，降低主射流卷吸伴随流的难度，加速两者之间的混合，导致半速度宽度快速增长。2) 在=2e之后射流半速度宽度基本保持不变，其长度与射流稳定段长度基本一致。3) 半速度宽度以较高速率线性增长，且在不同伴随流温度和流量条件下的增长速度相同。不同伴随流流量条件下射流半速度宽度分布趋势与图5(a)所示的相同。随着伴随流流量增大，伴随流速度增大，与超音速流的速度差减小，有利于二者之间的混合。

(a) 不同温度伴随流；(b) 不同流量伴随流

2.2 轴线静温分布

图6所示为不同伴随流温度和流量条件下超音速射流静温沿轴线的分布。射流离开喷管后出现重复波动，然后快速升温并趋近于环境温度。射流静温波动原因与射流速度波动原因相同，即伴随流影响了喷管出口的压力和温度。射流的静温是高速气体自身的温度，加上射流速度转化的温度就是射流的总温。与图4相比，射流静温的波动与射流速度的波动相反。超音速射流在运动过程中不断与周围气体发生热量交换，伴随流温度越高，超音速射流升温速度越快，静温越高。另一方面，随着伴随流温度的升高，超音速射流静温快速升高的位置不断延后，这是因为伴随流气体对超音速射流起包裹作用，能够减少超音速气流与周围气体的热交换。在不同伴随流流量条件下，超音速射流静温分布类似于不同伴随流温度条件下射流静温分布。伴随流流量越大，速度越快，对超音速主射流的封套作用越好，射流静温快速升高的位置距离喷管出口越远。

图7所示为不同伴随流温度和流量条件下超音速射流的静温分布云图。从图7可以看出：伴随流使超音速射流与外界环境隔绝，对超音速射流起封套作用，从而延迟超音速射流与外界环境的热量交换，使超音速射流维持较低的静温。

2.3 涡量和湍流强度

涡量是衡量流体单元在流场中旋转的指标，同时也是衡量流体混合程度物理量。涡量越大，混合程度越高。超音速射流在遇到周围环境气体时，在射流的边界由于速度梯度的存在而出现旋流。图8所示为在不同伴随流温度和流量条件下/e=1，7和13处沿径向()的涡量分布。在/e=1处，普通超音速射流直接与周围静止气体混合，在径向距离轴线0.5e处涡量达到最大值。但当环绕不同高温伴随流时(见图8(a))，集束射流涡量沿径向方向呈现“三段式”分布，出现3个波峰：1) 超音速主射流与周围伴随流气体混合，涡量达到第1个峰值。由于高温伴随流气体产生的低密度环境，减少超音速主射流与周围气体的混合效应，使超音速主射流的涡量小于普通超音速射流的涡量。2) 伴随流气体与超音速主射流发生混合，出现第2个峰值，伴随流气体温度越高，涡量峰值越大。3) 最外层第3个峰值是伴随流气体与周围静止气体发生混合，因此，其涡量较大。当环绕不同流量伴随流时(见图8(b))，小流量的伴随流气体(0.01 kg/s)不仅使得超音速主射流涡量降低，而且使涡量沿径向向外平移，但随着伴随流流量的不断增加，涡量曲线朝着“三段式”分布发展，在伴随流流量增大的过程中，伴随流速度变大，其与周围气体混合的效应不断增大。随着射流不断向前运动，在/e=7和13处，超音速主射流与伴随流气体充分混合，射流涡量分布沿径向向外移动，集束射流与普通超音速射流的涡量分布趋于 一致。

(a) 不同温度伴随流；(b) 不同流量伴随流

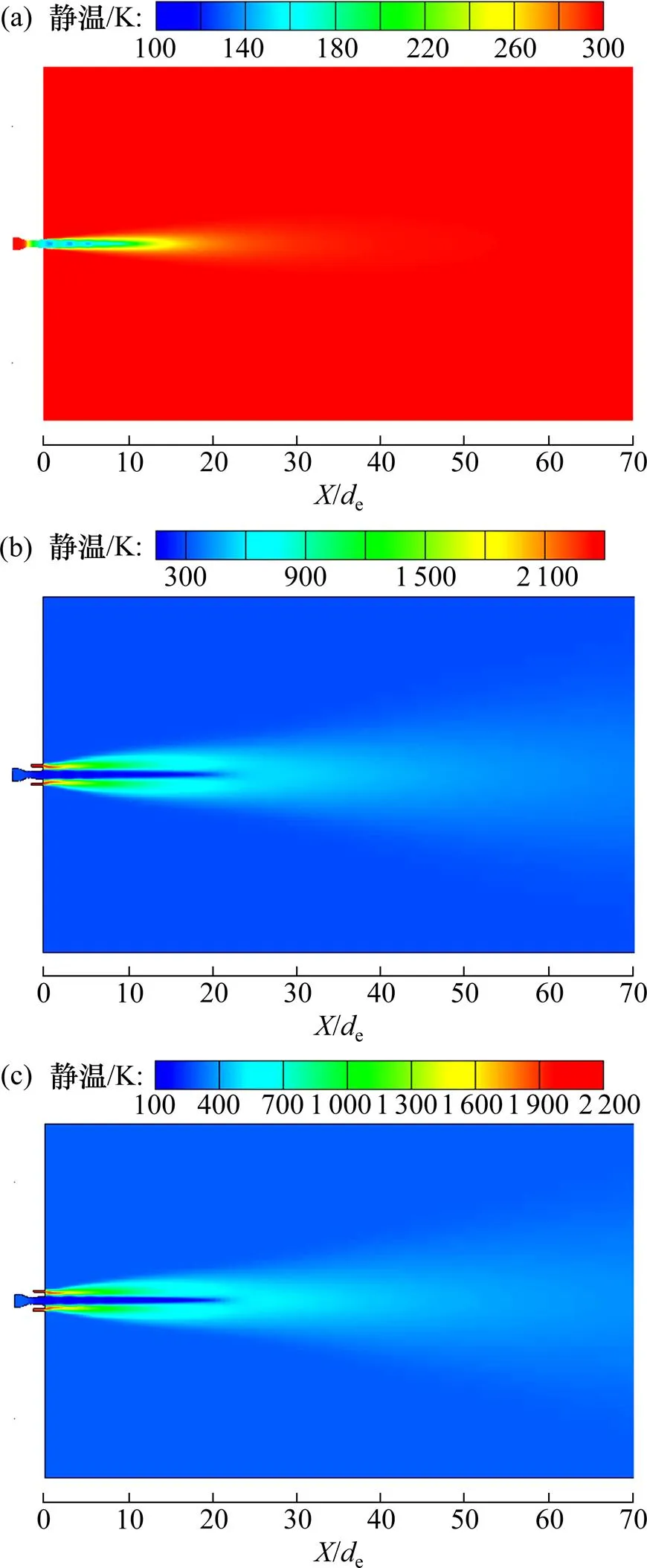
(a) 无伴随流；(b) 伴随流(2 500 K，0.05 kg/s)；(c) 伴随流(2 000 K，0.05 kg/s)

图9所示为不同伴随流温度和流量条件下超音速射流湍流强度的云图。超音速射流离开喷管出口后与周围气体发生混合，在射流向前运动过程中湍流强度不断增大。在无伴随流条件下，超音速主射流在10e之前保持较低的湍流强度(见图9(a))，而在集束射流条件下，超音速主射流可在20e范围内保持低湍流强度(见图9(b)~(c))。在环绕伴随流条件下，超音速主射流首先与伴随流发生混合作用，导致两者交界处气流湍流强度较大；伴随流温度越高、流量越大，湍流强度越大，范围也越大。高温和大流量伴随流能够有效抑制超音速主射流与外界环境气体的混合，使超音速主射流的湍流强度维持在较低水平。

(a) 不同温度下X/de=1处涡量分布；(b) 不同温度下X/de=7处涡量分布；(c) 不同温度下X/de=13处涡量分布；(d) 不同流量下X/de=1处涡量分布；(e) 不同流量下X/de=7处涡量分布；(f) 不同流量下X/de=13处涡量分布

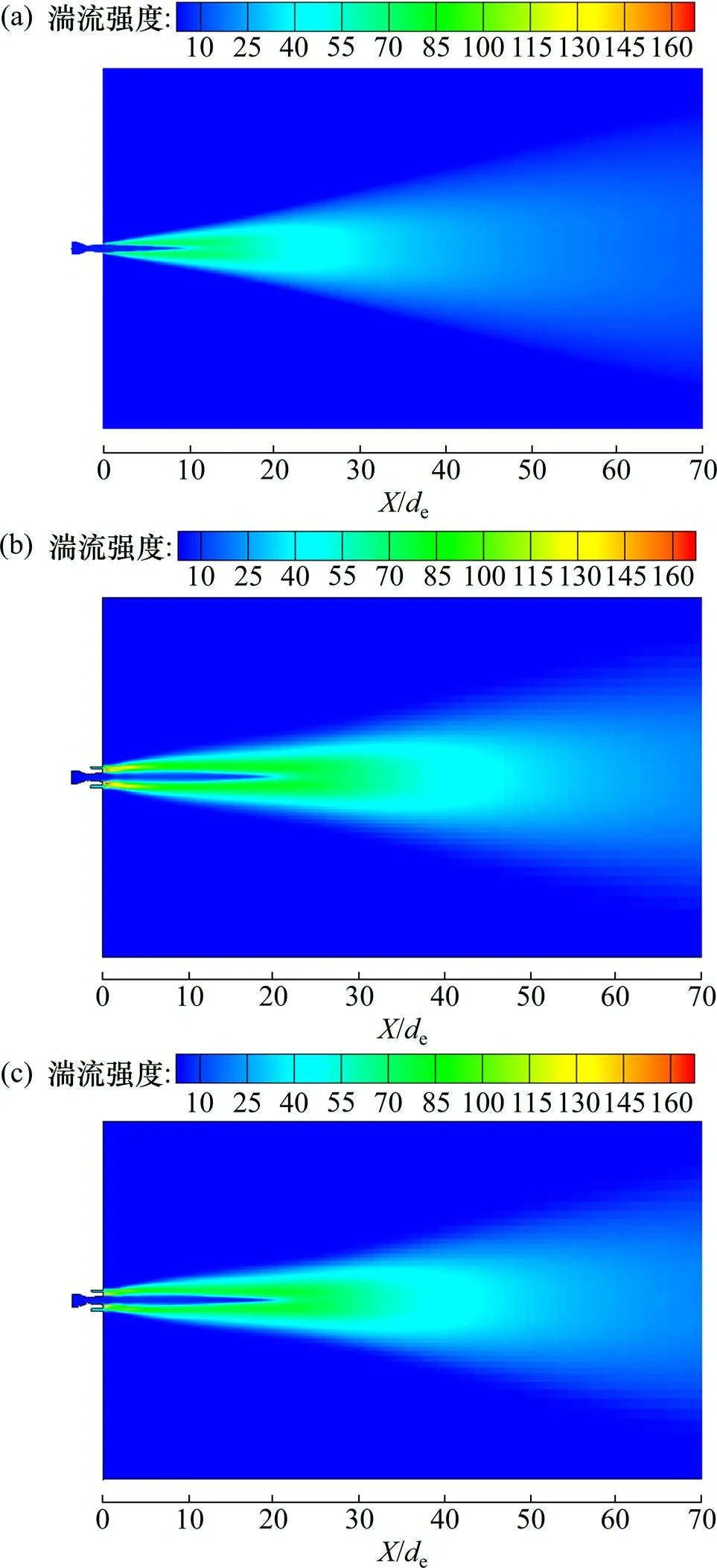
(a) 无伴随流；(b) 伴随流(2 500 K，0.05 kg/s)；(c) 伴随流(2 000 K，0.05 kg/s)

3 结论

1) 伴随流气体影响喷管出口温度和压力参数导致超音速射流速度和温度出现重复波动。与普通超音速射流相比，集束射流速度稳定段长度由10e增大到15e以上，且随着伴随流气体温度的升高，射流速度和温度稳定段长度不断变大。

2) 在伴随流条件下，集束射流半速度宽度的分布不同于普通超音速射流的分布，分为3个阶段：首先，从离开喷管出口后快速增长，伴随流温度越高、流量越大，增加速率越快；然后，在2e后射流半速度宽度基本保持不变，其长度与射流稳定段长度基本一致；最后，以较高速率增大。

3) 伴随流气体对超音速主射流起到封套作用，能够改变超音速射流涡量和湍流强度的大小和分布，减少超音速主射流与周围气体的混合效应，降低主射流的涡量，并在更长距离内保持较低的湍流强度。

[1] DEO B, BOOM R. Fundamentals of steelmaking metallurgy[M]. New jersey, USA: Prentice-Hall, 1993: 35−40.

[2] NAITO K, OGAWA Y, INOMOTO T, et al. Characteristics of jets from top-blown lance in converter[J]. ISIJ International, 2000, 40(1): 23−30.

[3] TAGO Y, HIGUCHI Y. Fluid flow analysis of jets from nozzles in top blown process[J]. ISIJ International, 2003, 43(2): 209−215.

[4] WANG W, YUAN Z, MATSUURA H, et al. Three-dimensional compressible flow simulation of top-blown multiple jets in converter[J]. ISIJ International, 2010, 50(4): 491−500.

[5] MATHUR P C. Fundamentals and operating results of Praxair CoJet technology[J]. Iron & Steelmaker, 1999, 26(3): 59−64.

[6] MAHONEY W J, DENEYS A C, VARDIAN G T. High mach number, sub-atmospheric, coherent jets and their application in vacuum metallurgy[J]. Vacuum, 2008, 1: 8−11.

[7] SUMI I, KISHIMOTO Y, KIKUCHI Y, et al. Effect of high-temperature field on supersonic oxygen jet behavior[J]. ISIJ International, 2006, 46(9): 1312−1317.

[8] LIU Fuhai, SUN Dongbai, ZHU Rong, et al. Effect of shrouding CH4flow rate on flow field and stirring ability of coherent jet in steelmaking process[J]. Springer Plus, 2016, 5(1): 1613−1626.

[9] MEIDANI A R N, ISAC M, RICHARDSON A, et al. Modelling shrouded supersonic jets in metallurgical reactor vessels[J]. ISIJ International, 2004, 44(10): 1639−1645.

[10] ALAM M, NASER J, BROOKS G, et al. Computational fluid dynamics modeling of supersonic coherent jets for electric arc furnace steelmaking process[J]. Metallurgical and Materials Transactions B, 2010, 41(6): 1354−1367.

[11] LIU Fuhai, ZHU Rong, DONG Kai, et al. Effect of ambient and oxygen temperature on flow field characteristics of coherent jet[J]. Metallurgical and Materials Transactions B, 2016, 47(1): 228−243.

[12] ODENTHAL H J, BADER J, NÖRTHEMANN R, et al. The optimized SIS Injector for EAF Application[C]. AISTech 2014: The Iron & Steel Technology Conference and Exposition, Indianapolis, USA. 2014: 5−8.

[13] 袁章福, 潘贻芳. 炼钢氧枪技术[M]. 北京: 冶金工业出版社, 2007: 27−53. YUAN Zhangfu, PAN Yifang. Oxygen lance technology for steelmaking[M]. Beijing: Metallurgical Industry Press, 2007: 27−53.

[14] VERSTEEG H K, MALALASEKERA W. An introduction to computational fluid dynamics: the finite volume method[M]. New York, USA: Pearson Education, 2007: 46−52.

[15] WILCOX D C. Turbulence modeling for CFD[M]. La Canada, CA: DCW Industries, 1998: 38−43.

[16] BALABEL A, HEGAB A M, NASR M, et al. Assessment of turbulence modeling for gas flow in two-dimensional convergent-divergent rocket nozzle[J]. Applied Mathematical Modelling, 2011, 35(7): 3408−3422.

[17] MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598−1605.

[18] ANDERSON J D, WENDT J. Computational fluid dynamics[M]. New York, USA: McGraw-Hill, 1995: 67−72.

[19] 张德良. 计算流体力学教程[M]. 北京: 高等教育出版社, 2010: 56−62. ZHANG Deliang. A course in computational fluid dynamics[M]. Beijing: Higher Education Press, 2010: 56−62.

(编辑 伍锦花)

Coherent jet characteristics under different shrouding gas conditions

ZHAO Fei1, SUN Dongbai1, ZHU Rong2, YANG Lingzhi3

(1. National Center for Materials Service Safety,University of Science and Technology Beijing, Beijing 100083, China;2. School of Metallurgical and Ecological Engineering,University of Science and Technology Beijing, Beijing 100083, China;3. School of Minerals Processing and Bioengineering, Central South University, Changsha 410083, China)

The field characteristics of coherent jet and conventional supersonic jet was studied by numerical simulation and experiment under different shrouding gas parameter conditions. The results show that the temperature and pressure of the nozzle exit is affected by shrouding gas and it leads to velocity and temperature fluctuations of the supersonic jet. The low-density and high-speed environment produced by high temperature and high flow of the shrouding gas protects supersonic jet, and reduces radial expansion and axial velocity attenuation rate of the jet. The higher the temperature and flow are, the longer the velocity and temperature core length of the jet are. Compared with conventional supersonic jet, the distributions of half-jet width and vorticity are changed by shrouding gas. With the high temperature and flow of the shrouding gas, the turbulence intensity of the jet maintains at low level over a long distance.

shrouding gas; supersonic jet; flow field characteristics

10.11817/j.issn.1672−7207.2018.02.004

TF724.3

A

1672−7207(2018)02−0282−08

2017−03−18；

2017−05−29

国家重大科学仪器设备开发专项(2011YQ14014505)；中央高校基本科研业务费专项资金资助项目(FRF-AS-17-004) (Project(2011YQ14014505) supported by the National Key Scientific Instrument and Equipment Development Funds; Project (FRF-AS-17-004) supported by the Fundamental Research Funds for the Central Universities)

杨凌志，博士，讲师，从事电弧炉炼钢过程模拟与工艺研究；E-mail：yanglingzhi@163.com