基于周期宽带参考信号的直接定位方法

杜剑平 余婉婷 刘广怡 沈智翔 于宏毅

(信息工程大学信息系统工程学院, 河南郑州 450001)

1 引言

在辐射源定位中,通常存在各种模型误差。例如转发器位置估计误差,系统混频器晶振频率误差,系统处理延迟误差,大气折射误差,同步误差等。基于已知部分先验信息的参考信号校正模型误差是定位技术中最常见的技术。通常做法包括:(1)离线标定方法。该方法在系统建立时或固定时间间隔,运用第三方手段对系统参数进行离线式标定,例如通过多站测轨纠正星历误差,利用电离层观测结果纠正大气折射误差。该方法实施成本和难度较大,实时性不佳。(2)参数差分技术。将参考信号和待定位信号的相同模型误差通过差分的方法去除,例如差分GPS(Global Positioning System)定位中通过差分消除大气折射误差[1]。(3)位置差分技术。将参考站信号定位结果与参考站实际位置的偏差作为位置补偿量,补偿到辐射源定位结果中。该做法只是近似结果,虽然便于实施,但性能不理想。

其中参数差分技术是应用最广泛的模型误差校正技术。例如无线测向应用中,通常采用已知位置的参考源估计出模型误差,并将该测量值直接补偿到测角结果中。辐射源定位中也会采用参考站发送参考信号的方式,估计出各种测量误差,之后将该模型误差带入未知目标定位中进行模型误差补偿[2- 4]。上述模型误差校准的基本原理都是利用已知部分信息的参考信号估计模型误差参数,之后运用差分的方法将模型误差参数补偿到定位所需的中间测量值中,运用两步定位法进行定位。参数差分技术的前提是基于观测数据能够准确地获得参数估计值。在低信噪比条件下,参数无法准确估计时,参数差分技术将无法消除模型误差的影响。

直接定位方法(DPD: Direct Position Determination)自从提出以来,受到相关学者的关注[5-7]。DPD方法相对传统两步定位方法(例如TDOA(Time Difference of Arrival),FDOA(Frequency Difference Of Arrival),DOA(Direction of Arrival)等)能够获得更高的定位精度,尤其是在低信噪比时,性能提升显著[8]。目前DPD的文献主要集中在特定场景和特定信号格式的DPD估计方法和性能分析[9-11],关于模型误差分析和校正的研究不多。Weiss在文献[12]中针对定位系统中的模型误差对定位精度影响一文中,分析了不同模型误差影响下,对定位精度的影响,得到DPD相对于两步定位法能够获得更好鲁棒性。但是文献中没有针对如何校准模型误差展开深入讨论。

DPD标准框架中,应将模型误差参数和辐射源位置参数作为待估计向量,运用所有接收站实际接收信号构建联合分布函数,采用最大似然方法,对参数向量进行联合估计。当样本数量趋于无穷时,该方法估计精度能趋于克拉美罗(CRLB:Cramér-Rao Lower Bound)估计精度。但实际应用中,为了不占用公共资源,通常采用极低信噪比的宽带参考信号进行模型误差校准。参考信号具有时间连续性,周期性,波形已知性,低信噪比性;而辐射源信号具有突发性,非周期性,波形未知性和较高信噪比的特性。将两类不同特点的信号进行联合参数估计的复杂度极大,且性能提升不显著。

本文设计一种在线实时模型误差参数标定方法。与离线模型误差标定技术不同的是,实时模型误差标定技术在定位的同时采集参考信号,利用参考信号和目标信号的相互关系,实时估计模型误差参数,适用于快速变化的模型误差参数标定,而离线误差参数标定通常采用第三方手段直接对模型误差参数进行逐一标定(例如卫星轨道光学测轨,电离层探测等手段),主要应用于缓变模型误差参数标定,无法适应快速变化的模型误差参数标定。此外,为了解决低信噪比条件下的模型误差标定问题和目标辐射源定位问题,分别建立模型误差参数直接估计模型和辐射源校正定位直接估计模型,以满足低信噪比下对定位精度的需求。相对于模型误差和辐射源定位联合估计方法,本文将模型误差参数估计和辐射源位置参数估计两个相对独立的参数估计问题分解开,并分别运用DPD框架进行求解,在保证两个估计问题在低信噪比条件下的性能的前提下,有效地降低了联合参数估计的复杂度。

文章的结构是:第2节阐述了利用参考信号校准模型误差的基本原理,将模型误差分为时延误差和频率误差,并给出时延误差和频率误差的校准方法。第3节针对系统时频差校准参数估计问题,首先提出了基于最大似然的估计方法并给出了其与互模糊函数的关系,之后为了提高时频差估计精度,提出了基于最大似然的超分辨率时频差直接估计方法。第4节针对系统时频差估计中参考信号的周期性、信噪比低,带宽宽,数据量大的特点,提出了一系列的加速策略。第5节给出了基于参考信号模型误差估计的DPD模型误差校正模型和算法。第6节给出了一个仿真算例,分别从计算复杂度和精度说明算法的有效性。

2 模型误差消除的基本原理

本文以多星定位为例,说明模型误差的消除方法。该定位体制下,目标信号经过卫星模拟转发后被地面接收设备接收。模拟转发过程中,卫星只对转发信号进行放大和变频,不改变调制方式,且没有路由排队过程,所以转发过程可能产生一个相对比较稳定的转发延迟和转发频率变化量。文献[4]中详细分析了卫星定位系统的各种误差来源,并定量分析各种误差对定位精度的影响。针对一个典型的无源卫星定位系统的模型误差包括:(1)系统处理延迟误差(包括转发器处理延迟和接收机处理延迟);(2)系统混频本振误差(包括转发器混频本振和接收机混频本振);(3)转发器位置和速度估计误差;(4)大气折射误差(对流层和电离层传输延迟误差);(5)接收机位置和速度误差;(6)采集设备同步和采样间隔误差(如图1所示)。

其中大气折射误差在最严重折射导致的延迟估计误差仅为ns级别,可以忽略不计;接收机位置和速度误差可以通过前期精细标定获得厘米级精度;接收站的采集设备通过GNSS(Global Navigation Satellite System)授时驯服铷钟能够获得5 ns级别的精度,该误差相对公里级别的定位精度而言可以忽略不计。本文重点研究前三种模型误差的校准方法。

消除模型误差的基本原理是使用已知位置的参考信号估计系统偏差,进一步代入未知目标定位中(如图2所示)。

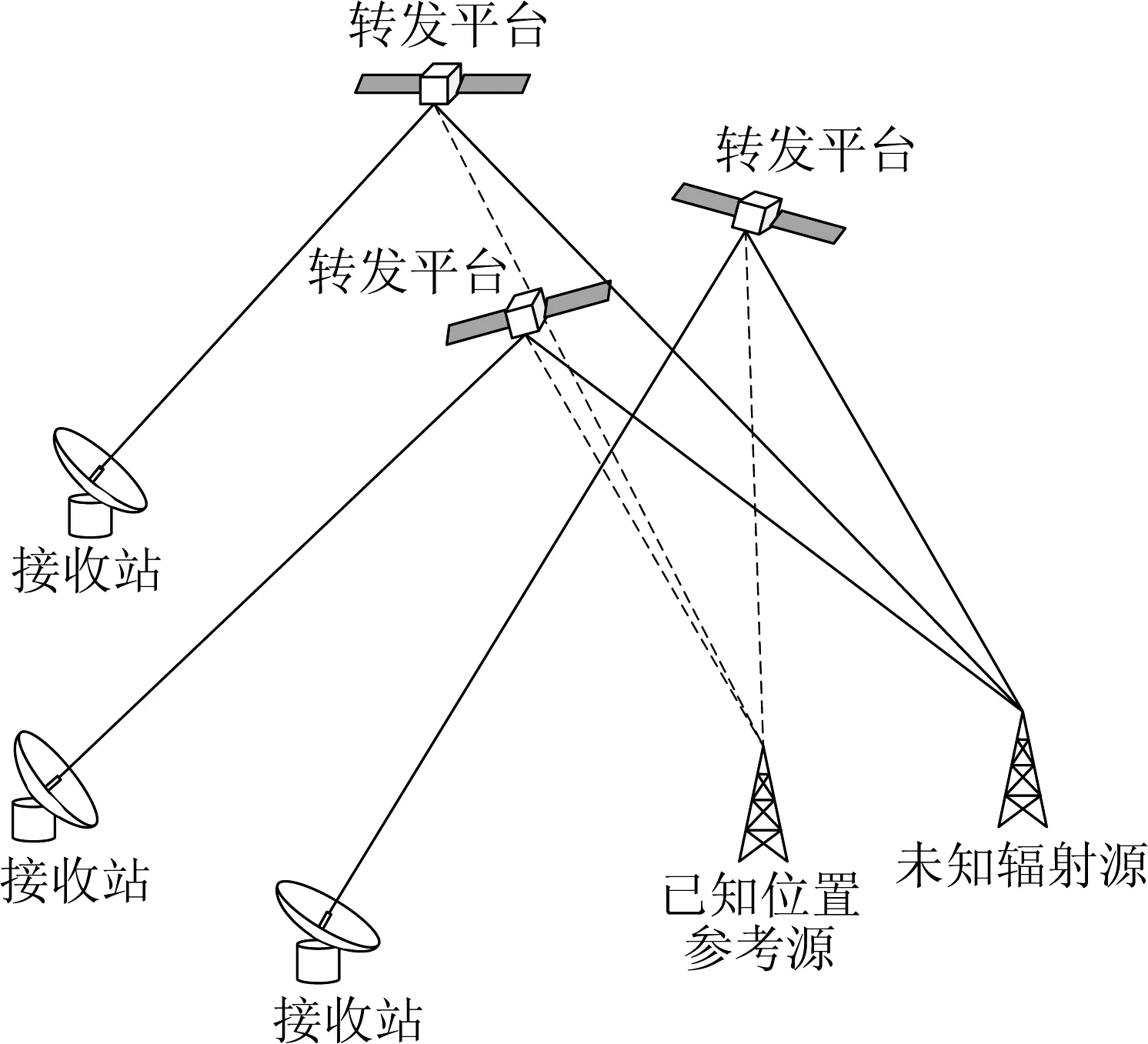
图2 模型误差校准基本原理

已知位置的参考信号源发送已知波形的信号,经由转发器转发、下变频后,被地面接收站接收。地面接收站下变频后正交采样,获得关于已知参考源信号的时域波形。系统根据接收信号和已知先验知识,估计链路混频误差和系统延迟误差,并将这两个量补偿到未知位置辐射源定位中,完成模型误差的校正工作。

2.1 系统时频差校准信号模型

(1)

(2)

其中t=t1,t2,…,tN,τr,τu是参考信号和待定位信号的传播延迟,fr,fu是参考信号和待定位信号的频率漂移,是参考信号和待定位信号复衰减系数。采用参考信号进行频率和时延校准的基本原理是:运用已知波形和位置的参考信号估计出延迟τr和频率fr的偏移量,并建立起参考信号与实际定位信号的延迟和频率偏移量之间的关系,进一步应用于实际信号时延τu和频率fu的校正。

基于参考信号系统模型误差校正的算法流程如图3所示。

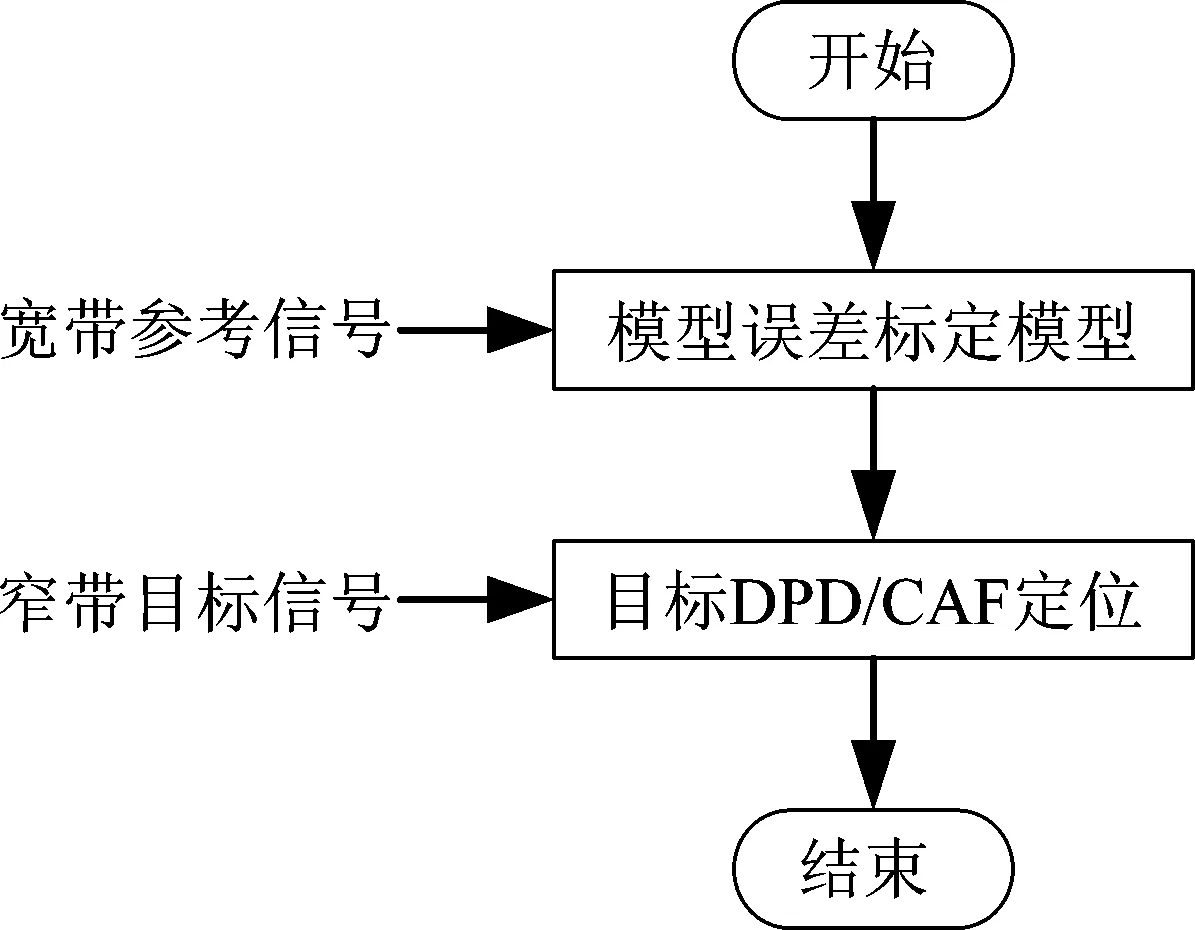
图3 基于参考信号模型误差校正流程图

定位系统基于接收到的宽带参考信号和已知波形的发送参考信号标定模型误差参数,并将该参数输入给针对辐射源窄带信号的DPD/CAF定位模型中。

2.2 系统时差校准模型

图4给出了定位系统各要素之间的位置关系和时差校准的示意图。

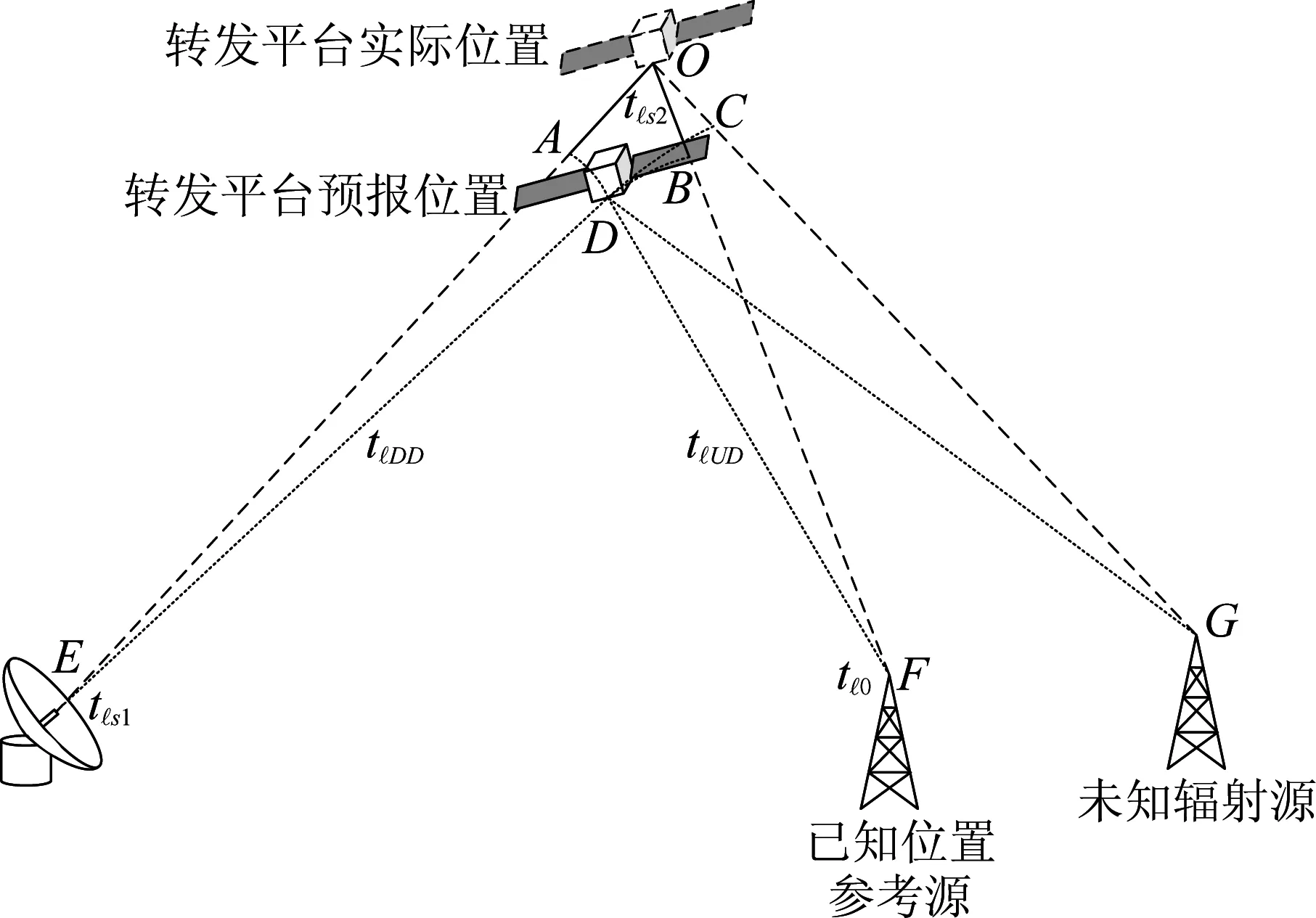
图4 时间差分示意图

图4中,参考信号的接收与发送的时差为:

(3)

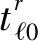
(4)

(5)

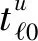
(6)

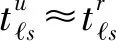
(7)

2.3 系统频差校准模型

导致不同接收站接收信号的频率不一致的原因主要有多普勒频移和下变频误差。接收参考信号和接收待定位信号的频率是:

fr=frs+Δfrd+Δfr

(8)

fu=fus+Δfud+Δfu

(9)

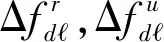
参考站的位置和速度已知(通常采用静止参考站),根据转发平台预报的径向运动速度即可估计出参考信号的多普勒频移量。假设转发平台的径向运动速度估计误差较小,导致多普勒频移估计误差较小。所以可以假设根据平台运动信息估计的多普勒频漂Δfrd的估计误差忽略不计,导致频率漂移不确定性的主要原因是下变频误差。

根据接收信号和发送信号的频移关系,可以计算得到fr-frs,根据转发平台运动规律即可计算得到多普勒频移量Δfrd,进一步可以得到下变频误差偏移量:

Δfr=fr-frs-Δfrd

(10)

导致下变频误差的主要原因是转发器混频器晶振的不稳定性和接收机混频器晶振的不稳定性。同一个转发平台的不同频段转发器的混频器通常采用一个晶振驱动,同一个接收机的不同频段也采用同一个晶振驱动,所以参考信号和待定位型号虽然处于不同频段,但混频偏移量是相同的。即Δfr=Δfu,

fu=fus+Δfud+fr-frs-Δfrd

(11)

与第一路差分后得到不同接收站相对于第一路接收信号的频率漂移量:

fu-fu1=(Δfud-Δfud1)+(fr-frs)-

(fr1-frs) -(Δfrd-Δfrd1)

(12)

其中(fr-frs)是路参考信号与发送参考信号的频差。

2.4 系统时差校准方法

采用最大似然直接校准模型误差并定位能够获得更好的定位效果,但需要付出更多的计算代价。尤其是参考信号信噪比极低时,需要累积足够多的数据,进一步增加了计算开销。实际应用中,模型误差参数相对稳定,可以持续观察并标定,而待定位信号为突发信号,需要根据各个突发进行定位,导致参考信号和待定位信号无法时间统一。本文采用两步校准法降低计算复杂度。首先运用参考信号估计模型误差参数,之后将该模型误差参数带入到目标位置估计中,再用最大似然法直接估计目标位置。

3 模型误差的最大似然估计模型

3.1 时频差的最大似然估计模型

最大似然法通过构建最大似然估计模型获得参数最佳估计:

(13)

其中r=[r(t1),r(t2),,…,r(tN)]T是路接收站的接收数据,s=[s(t1),s(t2),,…,s(tN)]T是发送数据向量,A是采样平移矩阵,其结构为:

(14)

其中IN-τ是(N-τ)×(N-τ)的单位矩阵,Iτ是τ ×τ的单位矩阵,τ是将参考信号s往后移动的样点数。F是频率校准矩阵:

(15)

b是混频导致的幅度-相位调节复标量。b的最小二乘估计为:

b=[(FAs)HFAs]-1(FAs)Hr

(16)

将式(16)带入式(13)

|r-FAs[(FAs)HFAs]-1(FAs)Hr|2

将目标函数展开后得到

(17)

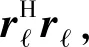
(18)

因为AFHFA=I,不妨设sHs=1,所以[(FAs)HFAs]-1=1,H=FAs(FAs)H。

(19)

(20)

将式(20)展开成和式,

(21)

若s(t),r(t)是实信号,τ=τ/fs,fs是采样频率,则:

c

(22)

式(22)即为实信号的互模糊函数。针对实信号而言,最大化互模糊函数估计时频差方法,实际上就是时频差的最大似然估计方法。

针对复信号而言,互模糊函数的表达式如式(20)。根据已知接收信号r(t),发送参考信号s(t),即可计算特定的τ, fd组合下的似然函数值,最大化似然函数,即可获得τ,fd的最优估计。

3.2 时频差的超分辨率估计模型

3.1中构建信号模型时,通过矩阵A对周期参考信号进行时间平移。该模型只能获得1/fs时间精度的时差估计。在文献[13-14]中也是采用采样点平移或者频点平移的方法进行时频差估计,这样做只能获得离散的时频差估计结果。在很多应用中,为了实现较大的基线,接收站间的距离较远。为了降低各站采集信号的回传通信开销,各接收站的采样频率fs不会太高。参考信号通常采用大带宽,长时间累积的方法,使理论时差估计精度远远优于1/fs,此时采样间隔成为制约时差估计的主要因素。

为了提高时差估计精度,构建超分辨率时频差估计模型估计接收参考信号与发送参考信号的时频差。超分辨率时频差估计的基本思想是在时域实施超分辨率频差估计,在频域进行超分辨率时差估计。设第个站的接收数据为r=[r(t1),r(t2),…,r(tN)]T,发送信号是s=[s(f1),s(f2),…,s(fN)]T,第个站的延迟和频移是τ和f,则:

r=FTHAsb

(23)

其中,b是路信道的衰减系数,是一个复常数。

A

(24)

是超分辨率时延校正矩阵,表示r由s延迟τ得到,其中

(25)

是傅里叶变换矩阵,

(26)

是频率校正矩阵。

根据式(23),b的最小二乘估计值为:

(27)

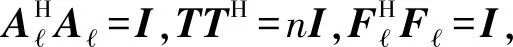
(28)

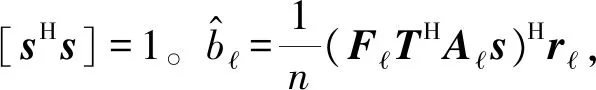
(29)

其中

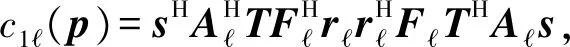
maxc2(p)=sHQs,

(30)

带入已知信号s, 实际接收信号r,待估计参数τ, f即可获得最大似然估计的评价函数c2(p),最大化评价函数,即可获得τ, f的最大似然估计。

在实际实现时,傅里叶变换矩阵可以运用FFT代替以提高计算速度。

4 模型误差估计的加速算法

模型误差估计模型式(30)的计算量与数据长度、时差分辨率和频差分辨率有关。本节首先分析模型误差估计的复杂度,之后给出若干加速计算的方法。

4.1 模型误差估计计算复杂度分析

在给定信噪比γ1,γ2和带宽B的条件下,数据量越大,时频差估计精度越高(代价函数的主峰越尖锐),时频差估计标准差为[15]:

(31)

其中T是数据长度。此外,(31)的计算精度计算依赖于时差τ和频差f的遍历精度。因此要获得高精度的时频差估计,需要极大的计算量。文献[4]中直接对来自不同转发平台的两路参考信号进行时频差估计,利用参考信号位置、转发器位置和接收站位置对不同路径的时频差初值进行预估计,并基于先验信息获得参考信号的时频差区间,得到结论是参考信号的时差搜索区间只需要在理论时差的[-1000 μs,1000 μs]区间即可。本文中选用的参考信号是超低信噪比的周期信号,直接对两路接收到的参考信号进行时频差估计时将因为信噪比过低而无法出现显著的互模糊函数(CAF:Cross Ambiguity Function)峰值。

为了提高估计精度,利用参考信号波形已知特点和式(31)结论,将各路信号与已知模型的参考信号进行联合时差估计,进一步获得不同路径参考信号的时频差。根据式(31),这样做理论上可以获得约3 dB的信噪比增益。

将接收参考信号与已知波形的参考信号进行时频差估计就需要搜索参考信号的整个周期。针对同步轨道卫星定位应用,最大传输延迟达到0.27 s,因此参考信号周期必须设计大于0.27 s,此时导致参考信号时频差搜索区间很大,遍历搜索无法满足需求。

由于CAF的时域主峰宽度与带宽的倒数相同,当按照奈奎斯特采样时,时域主峰宽度仅为1个采样间隔,所以CAF峰值搜索时必须逐采样间隔搜索,否则就会漏过时域主峰。CAF的频域主峰宽度为信号时间的倒数。为了获得足够显著的CAF峰均比,需要积累足够长的数据,进而导致CAF的频域主峰宽度很小,也就意味着CAF的频域搜索步长也必须足够小才能不漏过频域主峰。由于主峰的时域跨度和频域跨度都很小,导致CAF是一个典型的麦芒极值问题(如图5),无法通过设计优化搜索路径的方法降低搜索量。

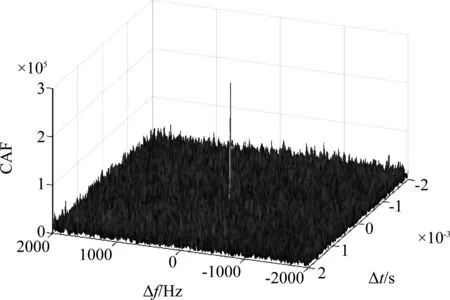
图5 麦芒极值问题示意图

本文通过分析CAF的特点,利用参考信号的周期特性提出一种时频差估计快速算法。该快速算法的基本原理是利用参考信号的周期性,对接收信号进行多周期对齐和能量累积,获得高信噪比的单周期的信号,再运用一小段高信噪比数据进行时频差估计获得时频差估计的粗估计结果,再运用较细网格进行局部搜索减小计算量。

4.2 周期信号能量累积

通过能量累积,将多周期信号时频差估计问题简化为单周期信号的时频差估计问题。将周期信号按照周期分段后,累积成一个周期的高信噪比信号,进一步用该高信噪比信号与已知的发送信号进行时频差估计,可以在不降低估计精度前提下,降低计算复杂度。

周期信号的能量累积过程,等价于多天线合成问题。将一个周期的信号看成是一副天线接收的信号,运用时频差对齐,衰减系数估计的方法进行多天线合成,能有效提高信噪比。

接收信号为r,假设参考信号的周期为p,将r按照p为周期分解为Q段,分别记为r1,r2,…,rQ。因为不同数据段之间只存在时差,不存在频差,因此只需要时间上对齐即可。各段信号之间满足如下关系:

rq=THAqsfbq

(32)

(33)

(34)

(35)

去除常数项并合并相同项得到:

(36)

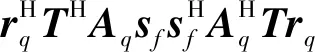
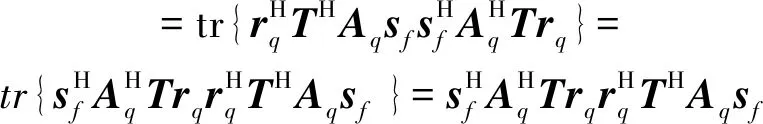
(37)

所以得到:

(38)

其中

(39)

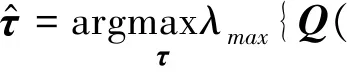
(40)

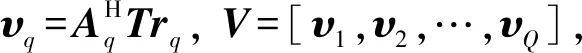
(41)

运用λmax{Q}=λmax{VVH}=λmax{VHV}的性质,即可将优化问题简化为:

(42)

此时将p×p矩阵的特征分解简化为Q×Q矩阵VHV的特征分解问题。通常周期数Q较小,矩阵VHV的特征值分解复杂度不高。

(Q-λmaxI)x=0

(43)

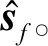
经过上述过程,可以得到高信噪比的频漂后参考信号估计值sf,此时能够实现不降低估计精度的前提下,将多个周期信号的时频差估计简化为单周期信号的时频差估计问题。

4.3 时频差分步搜索算法

基于4.1,可以在不降低估计精度前提下,将Q个周期的数据的时频差估计问题减小为单个周期的时频差估计问题。当单个周期数据长度较大时,时频差估计计算复杂度仍然难以接收。

由于CAF频域主峰宽度与时间长度有关,对于一个周期采样的CAF来说,由于周期较大导致主峰宽度较小,需要用很小的频率分辨率才避免错过最优频差估计。本文通过数据截取的方法,缩小数据长度计算CAF,有意降低CAF的频差分辨率,使CAF的频域主峰呈现出较大的宽度,再用较低的频域分辨率进行搜索,也不会漏过主峰。找到主峰大致位置后,在小范围内再用长,精细频域分辨率进行精密搜索,获得高精度的时频差估计。

运用短数据获得CAF频域较宽主峰的前提条件是CAF在主峰附近能够累积足够的能量。如果直接用实际接收的两路参考信号的短数据计算CAF,或者不进行周期信号能量累积,都将无法在形成显著的CAF主峰。

设小段数据长度为M,设发送参考信号为s=[s1,s2,…,sP+M]T。一个周期的接收参考信号是r=[r1,r2,…,rP]T,取长度为M的一段数据rM=[r1,r2,…,rM]T,计算如下所示代价函数:

(44)

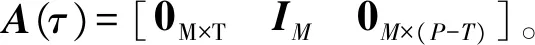
0M×T是M×T的全零矩阵,0M×(P-T)是M×(P-T)的全零矩阵,IM是M×M的单位矩阵。T=τfs, fs是采样频率。F是频率校准矩阵:

(45)

由于数据长度较短,频差估计精度下降,在最优时差估计点处的不同频差的代价函数形成光滑单峰而不是尖锐单峰。此时可以用较小的频差分辨率进行搜索仍然能够搜到代价函数的主峰。经过频差降分辨率以及较小M的F矩阵的计算,能够快速获得单周期的时频差估计初值。基于该初值,在初值附近运用式(30)进行超分辨率搜索,即可获得高精度的时频差代价函数。

5 基于参考信号的直接定位模型

理想的模型误差校准模型应该建立起所有接收信号关于待定参数(包括模型误差参数和目标位置参数)的似然函数,再建立联合概率分布,通过最大似然估计所有待定参数。但是直接估计的计算复杂度很大,难以实现实时定位应用。实际应用中,往往模型误差相对稳定,不需要每次定位都重新标定,只需要定期进行模型误差标定即可。为了减小计算复杂度,本文将模型误差参数标定过程与定位校准过程分开处理。

关于位置P的各个接收站接收信号为:

r=FTHAsb

(46)

其中A是试验校准矩阵,在式(24)中定义;T是傅里叶变换矩阵,在式(25)定义。

通过第3节的分析,根据式(11),可以得到:

(47)

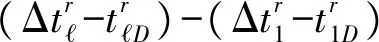
(48)

频率校准矩阵:

(49)

根据式(12),

(fr1-frs)-(Δfrd-Δfrd1)

其中(fr-frs)-(fr1-frs)-(Δfrd-Δfrd1)可以由参考信号标定获得由目标速度、转发平台预报速度和接收站速度计算获得。

F

(50)

式(50),(48)代入(46):

(51)

记S=A1s,待估计参数向量θ=[P,f1],其中P是目标位置,f1是第一个接收站的频率漂移,最小化负对数似然函数为:

(52)

与3.2节推导过程类似,式(52)化简为:

(53)

(54)

(55)

计算矩阵Q的最大特征值即可得到优化问题的解。由于Q的维度是N×N,当数据量极大时,复杂度较大,为了降低计算复杂度,定义υ

Q=VVH

(56)

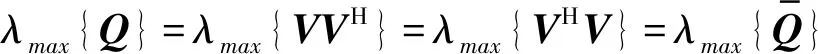
(57)

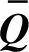
当给定辐射源位置θ后,根据模型误差标定结论,可以计算出υ和V=[υ1,υ2,…,υL],进一步计算出求解式(57)即可得到该位置θ的空间谱值。逐一计算感兴趣区域的空间谱,即可得到该区域的空间谱,从中找出显著的峰值,即为DPD方法找到的辐射源位置。

6 定位算例

为了验证算法性能,构造如下定位场景。目标辐射源位置为[N15°,E120°,16000 m],目标辐射源信号为突发式通信信号,每次通信持续1 s,辐射源信号为带宽为24 kHz的窄带高斯信号,接收站的采样速率为48 kHz。

参考站位于[N20°,E110°,5 m],参考信号带宽为20 MHz的BPSK调制伪随机信号,伪随机序列的周期是0.6 s,各接收站按照48 kHz欠采样参考信号。假设参考信号波形已知,每次参考信号采集时间长度为60 s,即每60 s更新一次模型误差参数。

参考信号采用宽带低功率信号的目的是避免能量集中在部分频带,便于隐藏参考信号。另一方面根据参考信号的实际信噪比和不同定位精度的需求,使用宽带参考信号,可以灵活选择参考信号采集卡的采集速率和采集带宽,在通信开销,计算复杂度和定位精度之间灵活折中。实际应用时,参考信号的频段覆盖目标信号所在的频段。接收站根据目标信号频点的位置,在临近空闲信道中(参考信号的频段内,但无其他通信信号的信道),选择一个与目标信号带宽接近的频率范围,对参考信号进行正交下变频,带通滤波和采样,得到等效的一个窄带的参考信号。

接收站并没有直接宽带采集参考信号,而实选取与目标信号带宽接近的窄带信号的原因,一是各个接收站分布范围较广,采样速率过大会给各个接收站之间的通信带来压力;二是目标信号的带宽只有24 kHz,目标信号的带宽限制了定位精度的提升,过高的参考信号时频差估计精度并不会给目标辐射源的定位精度提升带来更多的好处。三是参考采样速率过高,会导致定位过程的复杂度过高,难以满足实时需求。

三颗同步轨道卫星在起始时刻分别位于[N3°,E90°,35784 km],[S5°,E120°,35784 km],[N4°,E150°,35784 km],卫星瞬时位置和速度根据生成的TLE轨道根数计算获得。三颗同步轨道卫星接收站均为[N30°,E120°,5 m],三路信号的频率漂移分别为1000 Hz,50 Hz,-1500 Hz。三路信号的处理时间漂移为50 μs,75 μs,100 μs。假设星历预报的经纬度正确,高度偏差标准差为10 km。

本节首先对比直接定位方法与两步定位方法的定位检测门限和定位精度,之后对比不同参考信号参数下的定位精度和时间复杂度。

6.1 直接定位法与两步定位法的检测门限比较

在两步定位法中,系统实时检测两路信号的CAF,当峰均比超过阈值了,就启动定位程序。当信噪比过低,数据长度不够时,就会导致相关峰淹没在噪声中无法检测出信号。而直接定位方法实时绘制目标区域的空间谱,当空间谱的峰均比超过阈值,则认为检测到目标信号。本节从信噪比(SNR:Signal-Noise-Ratio)和数据长度的角度对比分析两种方法的检测门限。

当信噪比较低时,数据长度较短时,CAF无显著峰值时,就会出现漏警现象。图6～8给出了上述场景下两步法定位和直接定位的对比。

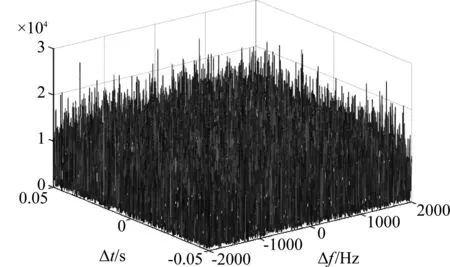
图6 SNR=-20 dB时两路信号的CAF

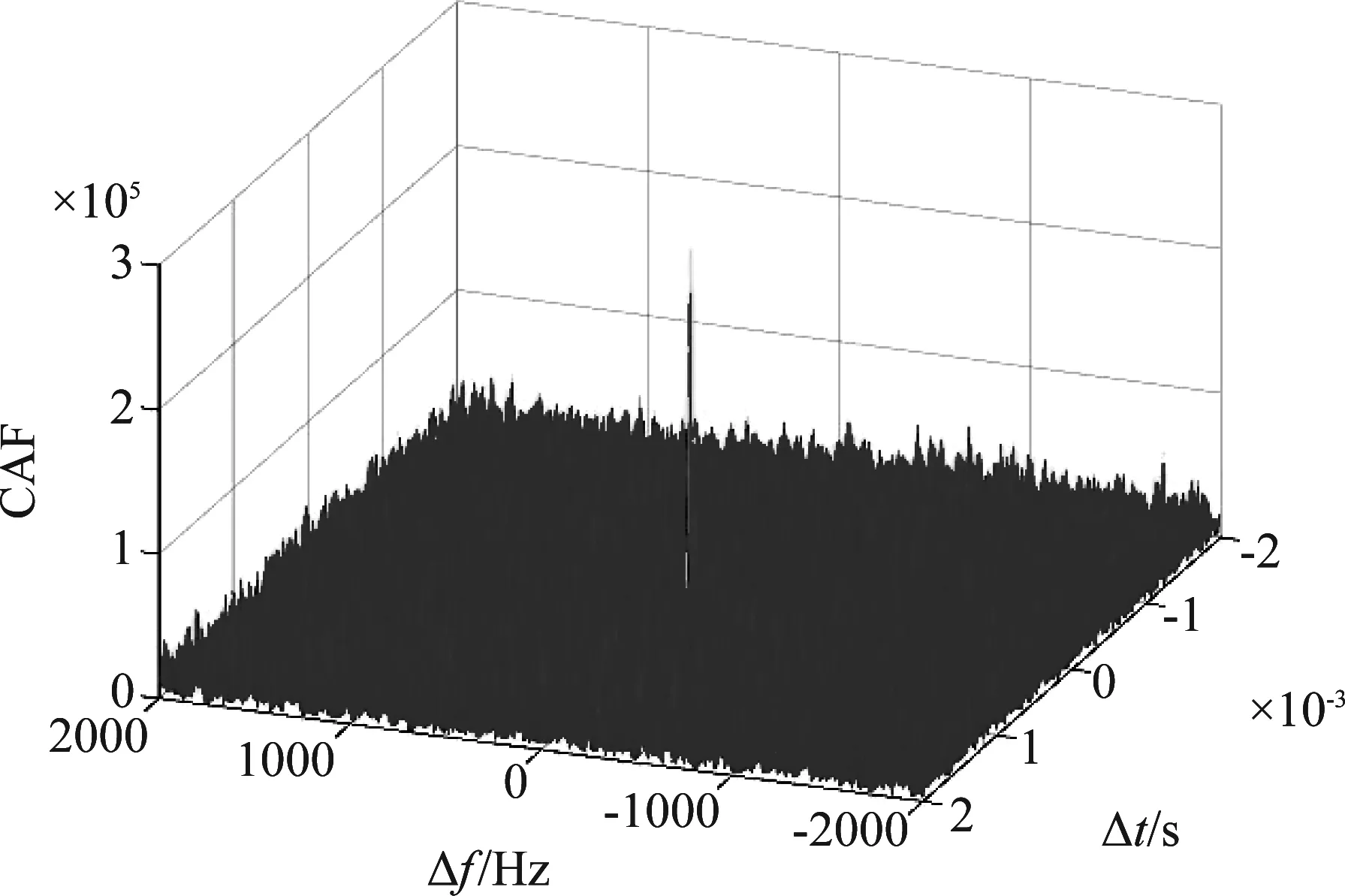
图7 SNR=-15 dB时两路信号的CAF

图8 SNR=-20 dB时直接定位法的空间谱

上述仿真中,目标信号通信时间持续1 s,目标信号的带宽为24 kHz,三个接收站的采样频率为48 kHz。图6和图7中,分别给出了SNR=-20 dB和SNR=-15 dB时的CAF,当信噪比较低时(SNR=-20dB),无法提取相关峰,当SNR=-15 dB时,才能产生较显著的相关峰。

在与图6相同的场景和参数下(SNR=-20 dB),综合三路数据,运用DPD获得的目标的空间谱如图8,在信号源真实位置处(N15°,E120°,16000 m)出现了较明显的峰值(假设已知目标高度,仅计算经纬度方向的空间谱)。得益于更多的数据和更多约束,直接定位方法在SNR=-20 dB就能检测出目标,而CAF在SNR=-15 dB才能从对比中可以看出直接定位法能够降低检测门限,准确地获得最佳的位置估计,避免了低信噪比下的漏警事件。

当信号SNR确定的条件下,数据越长,就能够累积出越显著的相关峰。图8对比了相同场景下(信号带宽是24 kHz,采样频率48 kHz),在不同定位数据时间长度时的检测门限。

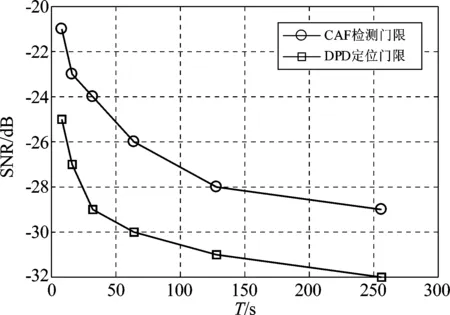
图9 正确提取时频差所需时长与SNR的关系

图9中CAF方法检测门限的标准是CAF能够累积达到20 dB峰均比;DPD定位门限的标准是空间谱在真实值附近1°的范围内有一个峰均比为20 dB的峰。

从图中可以看出,在3路信号场景下,在相同数据长度条件下,直接定位方法的定位检测门限要比CAF的检测门限低3～4 dB。这是因为CAF估计时频差时只能基于两路数据,而DPD能够整合所有数据直接获得位置估计。所以信号路数越多,直接定位法获得的性能增益越显著。

6.2 直接定位法与两步定位法的定位精度比较

根据式(31),时差估计误差标准差为:

(58)

(59)

上式是在采样频率无穷大时得到的结论,当采样间隔大于σT时,制约传统CAF方法的主要因素是采样间隔导致的误差。例如上述场景中,当带宽为24 kHz,两路信号信噪比为-20 dB,采样时间1 s,若采样频率足够高,并且能够获得足够多数据积累起CAF峰值,按照式(31)计算时差估计误差标准差为5.3012 μs,此时在本文定义场景下的CAF的测距误差标准差的理论值为2.1352 km。

由于CAF计算时,在时域采用逐个采样点遍历的方法,所以基于CAF的测距的精度受到采样间隔的制约。在本例中,采样率为48 kHz时,实际采样间隔为20.833 μs,大于理论时差估计误差的5.3012 μs。此时定位误差标准差约为8.5742 km。大于理论定位误差的2.1352 km。针对频率估计的分辨率也有类似的结论。

图10给出了不同信噪比下直接定位法与两步法定位精度的比较。

图10中的定位误差的方差计算方法为定位结果的协方差矩阵的迹。仿真中假设三路信号的信噪比相同,信号带宽24 kHz,采样速率为48 kHz。统计结果为100次随机仿真统计获得。从图中可以看出,DPD方法采用超分辨的时频差对齐方法,能够接近该定位问题的CRLB,其中CRLB的推导在文献[16]中有具体说明。运用CAF进行两步定位时,首先基于两路数据计算CAF,找出相关峰位置作为这两路信号的时频差(TDOA和FDOA)再运用最小二乘方法求解辐射源位置。CAF的仿真中,由于采样速率不够高,当信噪比较低时(SNR<-15dB)已经无法累积显著的CAF峰值,导致定位结果不可信,而当信噪比足够高时(SNR≥-15dB),影响定位精度的主要因素是采样间隔,信噪比的提升无法进一步提高定位精度。在仿真中,当SNR=-25 dB,时间长度为1 s时,DPD方法有较大概率无法获得准确定位结果,所以-25 dB条件下的DPD定位结果也不可信。

6.3 参考信号对定位精度的影响

运用参考信号能够有效地减小星历误差、系统处理延迟误差和系统混频误差等因素带来的影响。图11对比了基于CAF时频差补偿的校正方法和基于直接定位补偿的时频差校正方法。

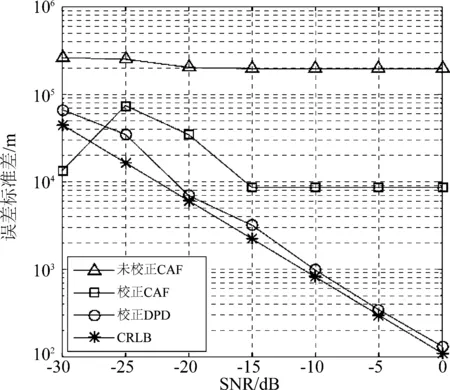
图11 参考信号校正模型性能对比分析

图11中的参考信号时间长度是60 s,参考信号SNR=-30 dB。从图11中可以看出,通过参考信号校正,不论CAF方法还是直接定位方法都能有效提高精度。当信噪比较高时,直接定位补偿方法能接近CRLB(由于运用单个参考信号无法彻底消除星历误差,模型中假设参考信号源与目标源距离不远,因此图中CRLB为无系统偏差模型下的CRLB)。CAF方法受到采样间隔的约束,信噪比的提升无法进一步提高定位精度。当信噪比较低时(SNR<-15 dB时),由于CAF无法准确提取时频差,定位结果不可信。

图12对比了不同带宽参考信号对定位精度的影响。

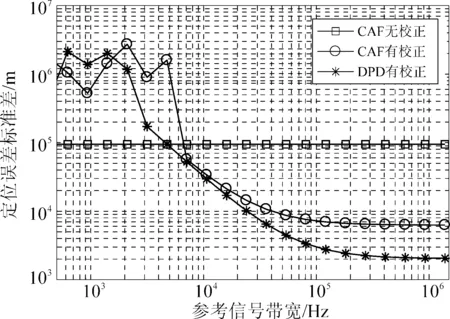
图12 不同参考信号带宽对定位精度的影响

图12的仿真中,参考信号发送时都是20 MHz的伪随机信号,接收参考信号时接收站对参考信号下变频后,选择不同带宽的带通滤波器从宽带参考信号中选出相应的窄带参考信号,再用相应的采样频率采集参考信号。仿真中目标辐射源信号的带宽都为24 kHz,采样速率都是48 kHz。上述仿真是随机产生200组参考信号并估计得到200组模型误差,带入目标信号定位模型中,统计平均的定位误差。从图12中,参考信号的带宽越大,基于参考信号的测距越准确,进一步利用参考信号进行模型误差的校正精度越高。但是,基于DPD的误差校正方法中随着参考信号带宽的逐渐提高,对模型误差校正性能提升的作用越来越不明显,影响定位精度的主要因素是目标信号的带宽。对于基于CAF的误差校正方法,随着参考信号带宽的增加,定位精度逐渐受到采样间隔的影响。当参考信号的带宽小于5 kHz时,采样速率为10 kHz,此时针对参考信号60 s的数据无法累计足够显著的相关峰值,所以无法准确估计出模型误差。所以上述仿真结果中带宽小于5 kHz的结果不可信。所以,若参考信号条件不好(信噪比较过低,或者带宽过窄等)校正结果反而会更差。图中未校正的方法中不论参考信号带宽的变化,定位精度都不发生变化。

6.4 参考信号时频差估计复杂度分析

从图9中可以看出,当两路信号的信噪比低于-26 dB时,需要超过1 min的数据才能累积出足够的峰值。根据频率分辨率为时间长度的倒数,模糊函数的频域主峰宽度为0.0042 Hz,此时需要频域搜索间隔小于0.0042 Hz。假设频率漂移的区间是[-2000,2000] Hz,则需搜索频点数为1.67×106。模糊函数的时域主峰宽度是带宽的倒数,即20.83 μs,针对天地联合定位应用,时间搜索范围是[-0.267,0.267] s,时间搜索点数为2.59×104。直接运用两路接收参考信号估计时频差总计搜索组合数是4.33×1010,每个组合需要进行2.88×106的复数乘法运算,合计需要约1.25×1017次的复数乘法运算。

本文没有采用直接根据两路接收参考信号估计时频差的方法,而是将参考信号与已知波形的信号进行时频差估计。这种做法能够在保持检测精度的前提下,将等效信噪比提升3 dB[4]。根据图7,此时所需数据长度约为15 s。进一步,将15 s的参考信号按周期分成25段,对齐,合成高信噪比信号,能够将时频差估计所需数据减小到一个周期,即0.6 s。

由于接收参考信号根据周期分段后已经基本对齐,只需要在一个采样间隔内进行超分辨率时差和衰减系数估计即可。超分辨率时差估计过程中,需要将接收参考信号运用FFT转换到频域,最后进行一个25×25的矩阵特征根分解和线性齐次方程组求解即可。运用一维搜索技巧(例如黄金分割搜索),能够进一步降低计算复杂度。由于同一路信号的频率漂移量相同,不需要进行频率域搜索,上述计算量相对于直接CAF方法可以忽略不计。

对齐后,首先用较短的数据长度(2000个)将CAF的频率主峰宽度扩大到24 Hz,设置频率搜索间隔为5 Hz,此时所需的时频差组合数是2.304×107,每个组合所需复数乘法次数是2000次,合计需要约4.6×1010次。找到时频差的粗估计结果后,在小范围内的时频差估计时,时域只需要前后10个采样点,频域只需在[-5,5]Hz范围内搜索即可,相对第一阶段搜索,计算复杂度可以忽略不计。

基于Matlab平台,分别运用基于两路数据直接计算CAF和本文方法,在相同计算精度的前提下,前者耗时约23 h,后者耗时约5 min。

7 结论

本文的主要工作是解决低信噪比,存在模型误差的辐射源卫星定位问题。本文的主要工作包括:

一是构建了辐射源直接定位模型,提高了低信噪比条件下信号检测定位的概率。直接定位模型能够综合利用所有信号之间的关系,获得比传统两步估计法更高的精度和更高的检测概率。通过仿真可以看出,在相同数据长度的条件下,直接定位法能够比传统两步定位方法(CAF)方法降低3～4 dB的信噪比要求。

二是构建了超分辨率的参数估计模型,实现定位精度不受采样频率影响。本文运用时域移频和频域移时的思想,构建了超分辨率的时频差估计模型,并分别运用在参考信号时频差估计和辐射源信号的时频差估计中。仿真结果表明,运用超分辨时频差估计模型能够使定位精度接近CRLB,而传统CAF时频差估计模型在信噪比和带宽足够高时,受限制于采样间隔,无法进一步提升性能。

三是构建了基于参考信号的直接定位模型,减小了模型误差对定位精度的影响。将基于参考信号估计的修正参数融合到直接定位模型中,用于补偿重构接收波形的似然函数,而不是补偿时频差参数。仿真结果表明,运用参考信号的直接定位模型基本能够消除模型误差的影响,定位误差能够接近无模型误差时的CRLB。而传统参数补偿方法在信噪比较低时,无法提取时频差参数时会导致定位失败,信噪比足够高时,受到采样频率的影响,定位精度无法获得提升。

四是给出了超分辨率的参考信号参数提取方法和加速方法,实现参考信号参数高分辨实时解算。利用参考信号的周期特性,将多个周期的参考信号按周期划分为多个信号,再借鉴多天线信号合成的方法,估计各个周期信号的时延偏差和最优加权系数,获得经过高信噪比的单周期信号。通过时域截取和频域截取的方法,使CAF的相关峰变宽,可以使用较大步长搜索到相关峰。之后再不断减小步长,提高估计精度,降低计算复杂度。在仿真分析中,遍历方法搜索时频差耗时约23 h,而加速算法耗时仅为5 min。