基于改进粒子群优化的四杆机构 运动轨迹误差研究*
杨 帆,周丽红
(武汉科技大学城市学院,武汉 430083)
0 引言
四杆机构在运动过程中,实际输出轨迹与期望运动轨迹存在偏差[1]。这种偏差若不重视,可能会导致四杆机构运动性能下降,从而造成重大的经济损失[2]。例如:夹持机器人的四杆机构受到运动轨迹精度的影响,导致物料定位不准确,产品质量不合格;飞机起落架的四杆机构受到运动轨迹精度的影响,导致飞机起落振动较大,对人的身体造成一定的伤害。因此,研究四杆机构运动轨迹误差,提高四杆机构运动轨迹精度具有重要的意义。
目前,对四杆机构运动轨迹理论的研究方法有多种。例如:文献[3]研究了四杆机构混合驱动动态轨迹的综合方法。分析了混合驱动机构的逆运动学,将传统设计理念和机器人设计理论有效结合,拓宽了四杆机构运动轨迹的研究范围。引用了阿苏尔杆组对机构进行仿真验证,提高了轨迹发生器的精度。文献[4]研究了四杆机构运动轨迹所产生的误差,并且对结果进行了仿真。建立了四杆机构简图模型,通过欧几里得距离误差函数推导出修正距离误差函数。对四杆机构几何运动参数进行优化,并且将优化结果进行误差仿真,修正距离误差函数可以提高四杆机构的运动轨迹精度。文献[5]研究了平面四杆机构运动轨迹的遗传算法。结合IC芯片粘片机焊头建立四杆机构优化变量的简图模型,构造了优化目标函数,采用遗传算法和MATLAB程序对四杆机构参数变量进行优化,从而得出最优值,实现了预定运动轨迹的输出要求。以往研究的四杆机构运动轨迹误差在某种程度上有所减少。但是,随着许多高精度加工企业的诞生,已经不能满足企业发展的需求。对此,本文引用了改进粒子群优化算法研究平面四杆机构的运动轨迹误差,建立平面四杆机构的运动简图,通过矢量方程式推导出运动轨迹点的坐标关系式。根据优化的参数变量构造出优化的目标函数,并且添加约束条件,采用改进粒子群优化算法对四杆机构几何参数变量进行优化,将优化结果输入到MATLAB软件中进行运动轨迹误差仿真,并且,与优化前误差仿真的结果进行对比和分析,从而为四杆机构运动轨迹的误差研究提供了参考依据。
1 四杆机构几何模型
四杆机构在平面坐标系中的运动简图及几何参数如图1所示。
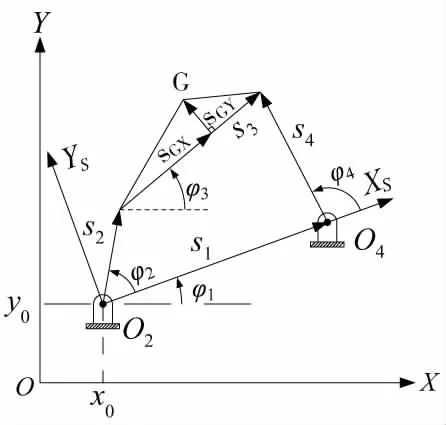
图1 四杆机构平面坐标系
在图1中,固定机架点O2的横坐标和纵坐标分别用x0和y0表示,固定机架与横坐标之间的角度用φ1表示,输入角用φ2表示,连接点用G表示,固定机架的长度用s1表示,输入杆的长度用s2表示,连接杆的长度用s3表示,输出杆的长度用s4表示,连接点G的横坐标和纵坐标长度分别用sGX和sGY表示,连接杆s3与横坐标之间的角度用φ3表示。在平面坐标系中,由几何矢量关系式[6]可知:
s2+s3-s4-s1=0
(1)
用每个位置向量的复数符号代替,可以写出如下方程关系式[6]:
s2eiφ2+s3eiφ3-s4eiφ4-s1eiφ1=0
(2)
分离方程式(2)的实部和虚部,并且令φ2=0,则实部和虚部变为:
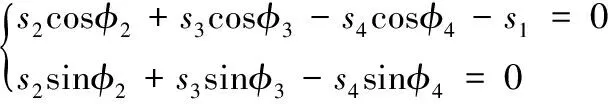
(3)
根据输入角φ2可以求解φ3、φ4,四杆机构的等式方程式如下:
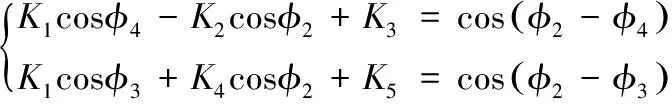
(4)
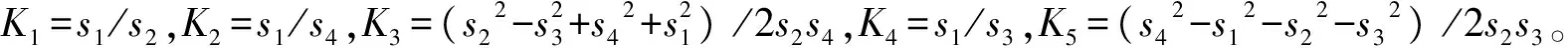
求解方程式(4)得:
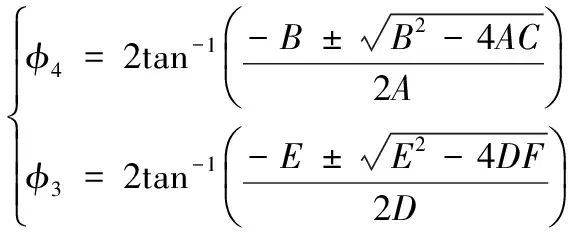
(5)
式中,A=cosφ2-K1-K2cosφ2+K3,B=E=-2sinφ2,C=K1- (K2+1)cosφ2+K3,D=cosφ2-K1+K4cosφ2+K5,F=K1+K5+(K4-1)cosφ2。
因此,连接点G在O-XY坐标系中横坐标与纵坐标关系式为:
(6)
式中,GXs=s2cosφ2+sGXcosφ3-sGYsinφ3,GYs=s2sinφ2+sGXsinφ3-sGYcosφ3。
2 目标函数
2.1 设计变量
四杆机构的输入杆在运动过程中,需要优化的设计变量参数分别为s1、s2、s3、s4、sGX、sGY、x0、y0、φ1和φ2。优化设计变量参数构成的矢量如下所示:
(7)
式中,φ2n是φ2的n等份位置角度。
2.2 目标函数及约束条件

(8)
在没有规定的时间内,φ2i作为四杆机构输入角度优化的设计变量,Gi是针对输入角φ2i一组值所设计的位置集合,如下所示:
(9)
因此,目标函数的第一部分表示为:
(10)
式中,N是合成点的数量。
目标函数的第二部分是从施加在四杆机构上约束条件导出的。因此,需要设置这些约束, 包括以下几个部分:
(1)根据四杆机构格拉晓夫准则的条件[8],必须有连杆能够做整周旋转运动,连杆的长度满足:
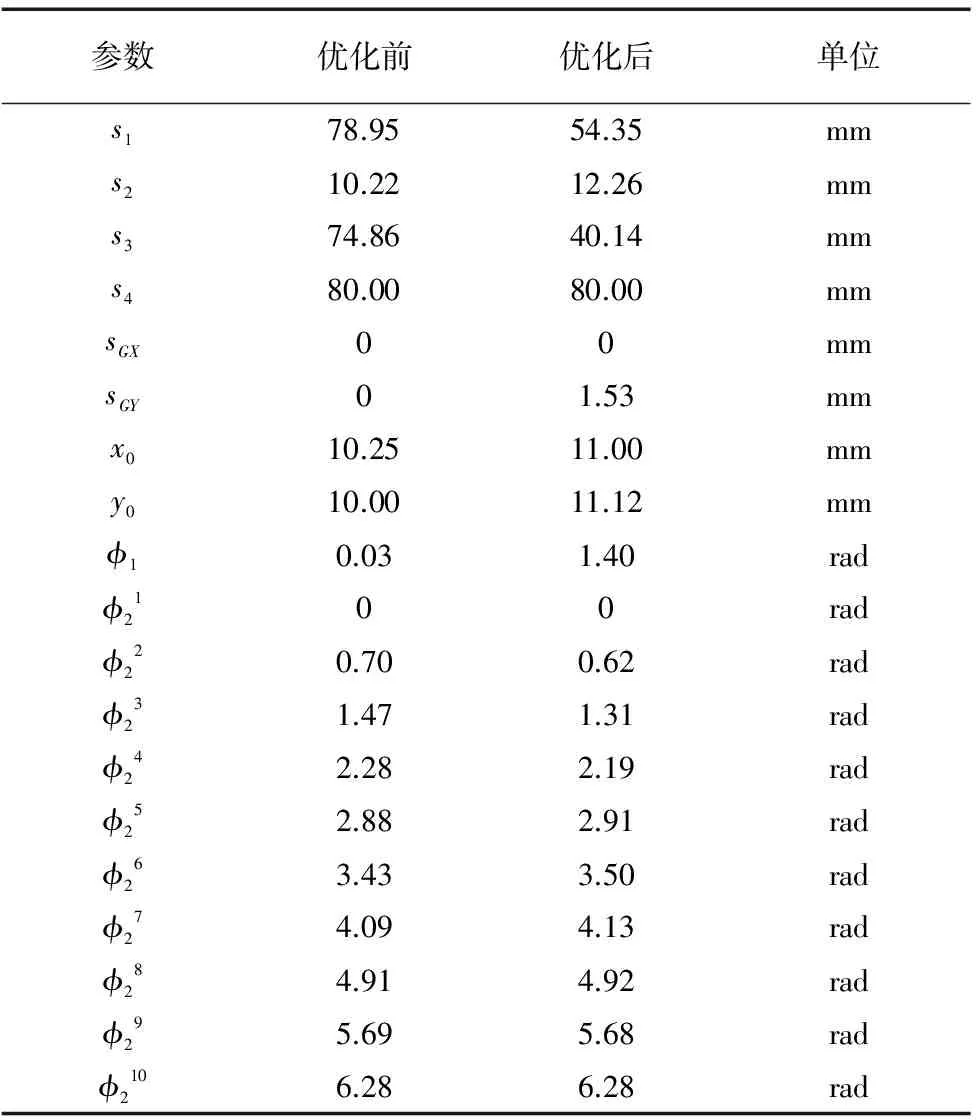
2mins1,s2,s3,s4+maxs1,s2,s3,s4 (11) (2)输入角度φ2i的序列必须进行排列,从最小到最大或者从最大到最小,φ2i角度范围为[0,2π]。 (3)设计参数变量范围必须为正值。 当优化值分配给设计变量X,并且将其它约束条件作为惩罚函数插入目标函数时,最终优化目标函数如下所示: (12) 式中,h1(X)=0表示满足四杆机构格拉晓夫准则,h1(X)=1表示不满足四杆机构格拉晓夫准则,h2(X)=0表示输入角φ2满足排列序列,h1(X)=1表示输入角φ2不满足排列序列,M1和M2表示惩罚目标函数的常数。 粒子群优化算法[9]缩写为PSO,是一种进化计算技术,主要是通过模拟鸟类在N维空间中寻找最优值。当粒子种群被定义后,则其中每个粒子在N维问题空间中的位置对应于优化问题的特定解。根据研究实际问题的需要,移动每个粒子的位置以获得权重。 在O-XY平面内,位置和速度计算采用以下等式[10]: (13) (14) 权重系数经过修改后的收敛速度更快,其方程式如下所示: (15) 式中,ωmax是初始权重,ωmin是最终权重,iter是当前迭代数,itermax是最大迭代数。 本文采用的改进粒子群算法具有约束因子方法,在约束因子方法中,通过修改约束因子χ,使得速度vi+1=χ(vi)。修改的约束因子增加了PSO的性能。 约束因子χ取值范围在[0,1]之间。 计算约束因子的公式如下所示: (16) 式中,κ取值范围在[0,1]之间,θ>4。通过适当地选择约束因子χ,速度可以保持在恒定间隔中而不超过设定速度。 约束因子值可以是固定的或随机变化的。为了提高该方法的有效性,可以选择与χ成反比的ω的值。改进速度方程如下: (17) 用于四杆机构运动轨迹误差的改进粒子群优化算法的流程图如图2所示。 图2 改进粒子群优化算法流程图 表1 四杆机构几何参数优化结果 图3 10个目标运动轨迹点 图4 横向误差仿真曲线 图5 纵向误差仿真曲线 根据图4仿真曲线可知,优化前,四杆机构横向实际运动轨迹与目标运动轨迹的最大误差值为1.2×10-3m;优化后,四杆机构横向实际运动轨迹与目标运动轨迹的最大误差值为0.8×10-3m;横向误差下降了33.3%。根据图5仿真曲线可知,优化前,四杆机构纵向实际运动轨迹与目标运动轨迹的最大误差值为1.7×10-3m;优化后,四杆机构纵向实际运动轨迹与目标运动轨迹的最大误差值为1.0×10-3m;纵向误差下降了41.2%。因此,本文采用改进粒子群优化算法优化四杆机构运动轨迹,横向和纵向运动轨迹产生的误差较小,提高了四杆机构运动精度。 本文研究了平面四杆机构运动轨迹误差,创建了平面四杆机构运动简图和二维坐标系,推导出运动轨迹点横坐标和纵坐标关系式。给出了优化设计的参数变量,构造目标函数并对目标函数添加约束条件。引用改进粒子群优化算法对四杆机构运动的几何参数变量进行优化,得出优化后的几何参数。将优化后的参数输入到MATLAB软件中进行仿真,确定出横向和纵向误差的仿真曲线。仿真结果表明,采用改进粒子群优化的四杆机构运动轨迹横向和纵向误差大幅度下降,从而提高四杆机构在实际生产中的定位精度。 [1] 成诚.平面轨迹机构的可靠性稳健设计[D].成都:西华大学,2014. [2] 王小琼. 弹性机构系统可靠性分析与稳健优化设计[D].沈阳:东北大学,2014. [3] 何东.一种新的动态轨迹综合方法的研究[D].沈阳:东北大学,2012. [4] 魏静.采用Matlab和误差函数法对轨迹生成四杆机构的优化及仿真研究[J].机械与电子,2016,34(1):11-14. [5] 覃金昌,孙惠玲.IC粘片机焊头四杆机构实现预定轨迹的遗传算法优化设计[J].桂林航天工业学院学报,2013(4): 375-379. [6] Radovan R Bulatovi,Stevan R Dorevi.Control of the optimum synthesis process of a four-bar linkage whose point on the working member generates the given path[J]. Applied Mathematics and Computation,2011,217(23): 9767-9775. [7] 杨帆.轨迹生成四杆机构优化及仿真研究[J].组合机床与自动化加工技术,2016(10):36-40. [8] M Khorshidi,M Soheilypour,M Peyro,et al.Optimal design of four-bar mechanisms using a hybrid multi-objective GA with adaptive local search[J].Mechanism and Machi-ne Theory,2011,46(10):1455-1463. [9] Arash Sardashti,H M Daniali,S M Varedi.Optimal free-defect synthesis of four-bar linkage with joint clearance using PSO algorithm[J].Meccanica,2013,48(7):1682-1691. [10] 段旭洋,王 皓,赵 勇,等. 基于嵌套粒子群算法的平面机构尺度综合与构型优选[J].机械工程学报,2013,49 (13):33-38.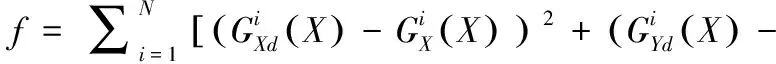
3 改进粒子群优化
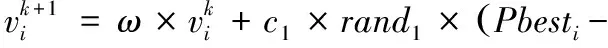

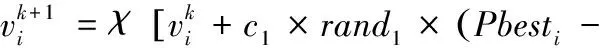
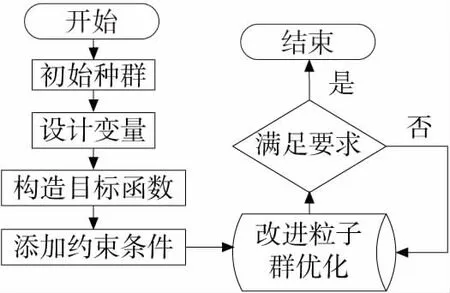
4 优化结果与仿真分析
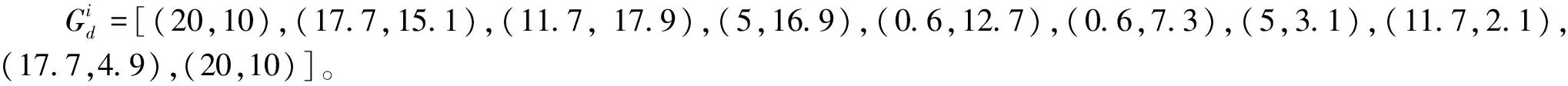



5 结束语

