不同预紧等级下滚珠直线导轨 副综合性能的试验研究*
周怡帆,韩 军,欧 屹,冯虎田
(南京理工大学 机械工程学院,南京 210094)
0 引言
滚珠直线导轨副的运动精度、振动特性、摩擦力以及噪声等综合性能参数作为评价导轨副的重要性能指标直接决定着被加工零件的质量及精度[1-2]。预紧力作为直接影响滚珠直线导轨副综合性能的关键因素之一,研究其对导轨副综合性能的影响具有十分重要的意义。
目前,国内外对导轨副预紧力与刚性相关的研究较多[3-4],王雷华等通过对静刚度的测试,分析得出,随着预紧力的增大,导轨副的静刚度也随之增加。日本的清水茂夫等也对滚动直线导轨副的静刚度进行了比较深入的理论和试验研究;在精度方面,徐烨等人研究得出,存在一个最优预加载荷,使导轨副的运动精度值最小,但缺少对导轨副俯仰角、偏摆角及滚转角的分析;在摩擦力方面,孙健利等人理论推导出了过盈量与摩擦力的关系,却未进行试验研究;在振动特性与噪声方面,国内外对其与预紧力的关联性研究较少。综上可知,目前国内在预紧力与导轨副精度、振动特性及噪声等方面鲜少研究,并且缺乏试验的验证。因此,能否应用于工程实践还需进一步验证。
当前行业无法实现预紧力的直接测量,只能通过摩擦力来间接反映。因此本文首先分析了预紧力的产生机理,推导出预紧状态下摩擦力的计算公式,并通过试验验证确立预紧力与摩擦力的关系。其次,通过滚珠直线导轨副综合性能试验台,对空载状态下滚珠直线导轨副运动精度、振动以及噪声各性能参数进行测定,结合Hertz接触理论、Stribeck曲线关系等理论分析出不同预紧等级对其综合性能参数的影响规律。
1 预紧力产生机理分析
1.1 预紧力的目的
滚珠直线导轨工作时沿直线做快速地往复运动。没有预紧力的情况下,导向面间会存在间隙,导致导轨副刚性不足,快速起停时产生冲击振动,且噪声增大等不利的影响。因此,为了清除间隙,提高动态特性,必须对滚珠直线导轨副添加一定的预紧力[5]。
1.2 预紧力产生机理
将钢球设计得比规定尺寸稍大,从而实现滚珠、滑块与导轨体的过盈配合。根据Hertz接触理论, 此时钢球与轨道发生接触变形, 形成接触面, 从而产生内部载荷, 即预紧力。本文以四列滚珠单圆弧滚道系列导轨副为研究对象,建立模型[7]。以其中一列滚珠横截面为研究对象,添加预紧力前后的接触状态如图1所示。

(a)无预紧力(δ0=0)

(b)添加预紧力(δ0>0)图1 导轨副预紧力受力分析图
接触类型为两点接触,钢球有过盈尺寸,接触处产生弹性变形,导轨与滑块间产生相对位移,此移动量可分解为X轴与Y轴方向上的分量。如图1所示,α0为接触角,οci与οri分别为滑块内沟槽的曲率中心以及导轨上滚道的曲率中心;i表示滚珠序号;滑块与导轨沟槽半径为rc、rr。οci与οri间距离s0为:
s0=rc+rr-d0
(1)
d0为无预紧力时钢球的直径,钢球预变形量δ0为:
δ0=d-d0
(2)
d为滚珠实际尺寸,由公式(1)、公式(2)可知:
s0=rc+rr-d+δ0
(3)
滚珠与法线方向上的接触角由α0变为β0,οci与οri间距离s0在X轴与Y轴方向的投影分别为s0x、s0y:
s0x=2fdcosα0-(d+λ)cosα0+δ0xs0y=2fdsinα0-(d+λ)sinα0+δ0y
(4)
其中:λ为预压量。f为适应度(0.515~0.525)。
接触角β0为:
(5)
(6)
由Hertz接触理论,接触弹性系数ki为:
(7)
滚珠局部接触力F与弹性变形量α的关系为[8]:
(8)
其中,α为单个滚珠的变形量,单位mm;ν1、ν2为滑块与导轨材料的泊松比;E1、E2分别为滑块与导轨的弹性模量D,单位为GPa;μ为与刚性相关的系数;∑ρ/(mm-1)为滚珠与滑块滚动接触时的曲率和,∑ρ=ρ11+ρ12+ρ21+ρ22,ρ11、ρ12分别为滚珠上的两个主曲率,ρ21、ρ22表示滑块滚道面上的主曲率。
在滚道直线导轨副中,当滚珠、滑块与导轨所用材料相同时,将已知参数带入公式(8)中,此时有钢球预变形量δ0为:
(9)
η为弹性系数,将上式变形后,得出钢球载荷的表达式:
(10)
滚动体与导轨接触法线方向的反力为:
(11)
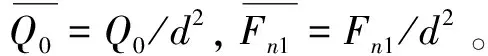
(12)
综上可推导出在预紧状态下,两点接触式四列滚珠单圆弧滚道导轨副的预紧拖动力Ff1可按下式进行计算:
Ff1=μFn1
(13)
其中,μ为滚动摩擦系数,一般可取0.002~0.005[4]。
2 试验台及试验方法介绍
2.1 导轨副综合性能试验系统
使用自主研发的滚珠直线导轨副综合性能试验台[9-10],实物如图2所示。

图2 滚珠直线导轨副综合性能试验台
图3为试验台架上安装的传感器示意图,用以动态测量导轨副运动精度、摩擦力、振动以及噪声各项参数:
(1)试验台架四周布置5个激光位移传感器用以测量滑块在行走过程中的运动精度;
(2)2个振动传感器分别布置于垂直于滑块顶面及侧面的两个方向上,用以测量滑块在行走过程中的振动特性;
(3)拉压力传感器一端通过双头螺柱与试验台架推臂相连接,一端通过带钢球头的螺栓与被测滑块柔性连接。当滑块运动时,拉压力传感器可测量摩擦滑块所受的驱动力,即摩擦滑块在运动过程中的摩擦力;
(4)噪声测量使用手持式高精度精密声级计进行测量,在图中未示。

图3 传感器布置示意图
2.2 导轨副综合性能试验方法
以GGB45BA系列滚珠直线导轨副为试验样件,微预紧p、轻预紧p1、中预紧p0三种不同预紧等级为变量进行综合性能各参数的测定。基本参数如表1中所示。

表1 预载类型
其中,C为额定动载荷,导轨副结构及性能参数如表2中所示。

表2 GB45BA结构参数及性能参数
试验过程:
(1)将试验导轨放入环境温度20℃,环境湿度50%的恒温室中不少于24h,使导轨副与室温到达热平衡;
(2)标定传感器,按照样品安装要求安装试验导轨,设置参数,充分跑合使润滑均匀;
(3)检测在各个速度下的导轨副运动精度、摩擦力、振动以及噪声各性能参数;
(4)多次测量以减少误差,同种状态下参数测定5次;
(5)对各测定参数进行相应的数据处理,以速度为横坐标,拟合出趋势曲线。
3 预紧等级与摩擦力的关系
采集1m/min~110m/min速度下的正反向摩擦力,拟合曲线如图4所示。

(a)正行程摩擦力

(b)反行程摩擦力图4 正反向摩擦力曲线图
试验结果显示:
(1)随着预紧力的增大,滑块行走过程中摩擦力增大。由公式(12)、公式(13)可知:
(14)
试验导轨为四列等载荷导轨,接触角β0与α0大小相近,因此将β0=45° 带入公式计算。其中Ff1为0.6m/min速度下导轨副的预紧拖动力测量值,由表1、表2知:
P0=0.1C=6.014kNP1=0.05C=3.007kNP=0.025C=1.5035kN
将各参数带入公式(14)得摩擦系数满足0.002~0.005的范围,理论推导出的预紧力与摩擦力关系得到验证。
(2)曲线不满足线性关系,由公式(13)可知,当预紧力一定时,摩擦系数的变化可引起摩擦力的变化。已知Stribeck曲线[11],如图5所示。
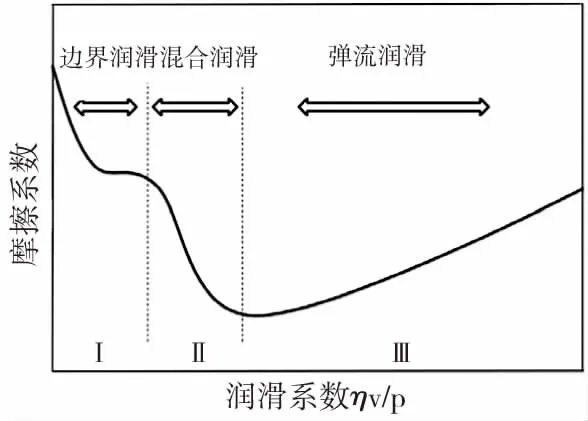
η —动力粘度,ν —速度,P—载荷图5 Stribeck曲线图
当所受载荷与动力粘度一定时,随着速度的变化,导轨副的润滑经历边界润滑、混合润滑与弹流润滑三个状态,摩擦系数先变小后增大。根据所测的试验数据结果及曲线图,可以看出:随着运行速度的增大,不同预紧条件下摩擦力均基本满足Stribeck曲线关系,实际与理论相契合。
(3)正反向摩擦力数值不同,表明导轨副正反向摩擦力存在差值,分析其与导轨副加工工艺有关。
4 试验结果分析
4.1 不同预紧等级导轨副运动精度的研究
测定1m/min速度下导轨的精度,取平均值。测量结果如表3所示。

表3 GGB45BA精度
表格数据显示:顶面平行度随着预紧等级的增大有增大的趋势;同时滑块在运动过程中俯仰角明显高于滚转角和偏摆角,表明滑块在沿导轨运动过程中其俯仰趋势较为明显;其余参数于预载等级无明显关系。
4.2 不同预紧等级导轨副振动特性研究
采集10m/min~70m/min每间隔10m/min速度下导轨副匀速阶段的振动信号,拟合成趋势曲线,如图6所示。

图6 不同方向上振动曲线图
(1)由公式(10)可知,在导轨副中,钢球预变形量δ0越大,预紧力Q0越大,对应公式(7)中导轨副的弹性系数k也越大。滚珠直线导轨副副频特性[12]为:
(14)
m为滑块质量,f阻尼系数,w为频率。由此可知,在相同激励信号下,弹性系数k增加,振幅增大。对比试验数据结果及曲线图可知:预紧力对滑块运动过程中振动特性有影响,且预紧力越大,振动越小。理论与实际相符合。
(2)在垂直于滑块行走方向的平面内,同预紧同速度条件下,垂直方向的振动量稍大于水平方向上的振动量,即滑块运动过程中,垂直方向的振动更明显。
4.3 不同预紧等级导轨副噪声特性研究
在距离导轨侧面1m位置每隔1m共布置3个噪声采集点,对比各采集点的噪声实测值,最大值为导轨副的噪声测量结果。测量结果如图7所示。

图7 不同预紧导轨副噪声曲线图
根据所测的试验数据结果及曲线图可以看出:
(1)导轨副高速运行时,轻预紧噪声小于微预紧状态下导轨副的噪声。中预紧状态下噪声标定值最大。表明适当增加预紧等级,由微预紧提示到轻预紧,导轨副噪声减小,预紧等级过大,噪声值增大。
(2)相同速度下,不同预紧的最大噪声差为2.3dB,表明预紧力对导轨噪声影响不大。提高运行速度,速度高于160m/min后噪声趋于稳定。
5 结论
本文通过预紧力产生机理分析,建立接触模型,理论推导出预紧状态下摩擦力的计算公式,确立预紧力与摩擦力的关系,并通过试验进行验证。最后对不同预紧等级下导轨副的综合性能参数进行测定,结合理论分析得出:
(1)预紧等级的不同对导轨的行走精度影响较小,无明显的关系;滑块在运动过程中俯仰角明显高于滚转角和偏摆角,说明滑块在沿导轨运动过程中俯仰趋势较为明显。
(2)导轨副振动随着速度的增加而增大,预紧等级越小,振动越大;且滑块运动过程中,垂直方向的振动更明显。
(3)导轨副高速运行时,适当增加预紧等级,由微预紧提示到轻预紧,导轨副噪声减小,预紧等级过大,噪声值增大;相同预紧状态下,160m/min后噪声趋于稳定。
综上所述,适当增加预紧等级,可降低滚珠直线导轨副运动过程中的振动特性及噪声,对运动精度的改变不明显,但会增加摩擦力。因此工程应用中应根据使用工况选择合适的预紧等级。
[1] 姜大志, 高飞. 直线滚动导轨预加负荷的应用研究[J]. 组合机床与自动化加工技术, 2007(4):38-40.
[2] Ohta H, Nakagawa T.Using Ceramic Balls to Reduce Noise in a Linear Guideway Type Recirculating Linear Ball Bearing[J]. ASME J. Tribol.,2003,125(3):480-486.
[3] 孙健利. 精密直线滚动导轨的预紧力及刚度计算[J]. 华中科技大学学报(自然科学版), 1988,16(6):127-132.
[4] Ohta H, Tanaka K. Vertical Stiffnesses of Preloaded Linear Guideway Type Ball Bearings Incorporating the Flexibility of the Carriage and Rail[J]. Journal of Tribology, 2010, 132(1):547-548.
[5] 李磊, 张建润, 刘洪伟. 直线滚动导轨副动态特性分析[J]. 振动与冲击, 2012, 31(18):111-114.
[6] 姜大志, 应强, 孙俊兰. 滚动直线导轨的受力分析与载荷计算[J]. 机床与液压,2008,36(4):270-272.
[7] A Dadalau, K Groh, M Reuβ,et al.Modeling linear guide systems with CoFEM: equivalent models for rolling contact[J].Computer Aided Engineering, 2012(6):39-46.
[8] 埃斯曼,哈斯巴根,韦根特. 滚动轴承设计与应用手册[M]. 刘家文.译.武汉:华中工学院出版社, 1985.
[9] 徐丹, 梁医, 冯虎田. 滚珠直线导轨副综合性能试验台测控系统设计[J]. 机械制造与自动化, 2016, 45(2):202-205.
[10] 徐丹, 梁医, 欧屹,等. 滚珠直线导轨副运动精度测试与分析方法研究[J]. 组合机床与自动化加工技术, 2015(1):126-129.
[11] Cheng D J, Yang W S, Park J H, et al. Friction experiment of linear motion roller guide THK SRG25[J]. International Journal of Precision Engineering and Manufacturing, 2014, 15(3): 545-551.
[12] Ohta H, Kitajima Y, Kato S,et al. Effects of Ball Groupings on Ball Passage Vibrations of a Linear Guideway Type Ball Bearing, ASME J. Tribol., 2007, 129(1):188-193.

