考虑柔性关节的刚柔耦合机械臂的优化设计*
尹秋明,范纪华,,3,谌 宏,王 琪,,3,方海峰,,3,吴群彪,,3
(1. 江苏科技大学 机电与动力工程学院,江苏 张家港 215600;2. 江苏科技大学苏州理工学院,江苏 张家港 215600;3. 张家港江苏科技大学产业技术研究院,江苏 张家港 215600)
0 引言
随着工业机器人在各种工况下的广泛使用,对机械臂工作精度和稳定性的要求也随之提高。机械臂的关节处常安装有力矩传感器和带有柔轮的谐波减速器等柔性元件,以达到精度高,传动效率高,减速比高等高性能要求。柔性元件的使用对机械臂运动精度产生不可忽略的影响,成为制约机械臂进一步发展的瓶颈[1-2]。
因此,柔性关节的振动抑制问题成为当今机械臂领域重点研究方向之一。Spong[3]首先提出柔性关节建模方法,将机器人的柔性关节简化成线性扭簧,并建立动力学分方程进行分析; BAHRAMI[4]推导出N根柔性杆的动力学方程,借助线性扭簧-阻尼模型,给杆底座施加随机激励,研究柔性杆末端动态的响应。在抑制柔性关节振动和控制方法方面,陈志勇等[5-6]根据关节柔性补偿和奇异摄动技术,设计了混合控制方案,引入柔性控制器来消除振动等不良影响。郭闯强等[7]在谐波减速器和机械臂的杆臂之间安装了一种新设计的力矩传感器,根据反馈信息,快速抑制振动。赵丹青[8]提出鲁棒自适应反演控制算法对柔性关节机械臂受扰动具有鲁棒性,从而实现较高精度的轨迹追踪。梁捷[9]在考虑柔性杆和关节的基础上,运用一种柔性控制器提高关节等效刚度,以达到抑制振动的目的。徐文福[10]以正弦一梯形函数为基础,表示出机械臂关节处的角速度,以函数的系数和幅值为变量,借助PSO算法优化得到变量的最佳数值,从而减小刚柔耦合机械臂末端振动。上述都是对带有柔性关节的机械臂抑制振动方面所做的一些研究。而在目前的研究中,关于考虑柔性关节的机械臂的优化设计相应尚少。
本文在Spong提出的线性扭簧模型基础之上,依据柔性关节的建模方法,建立柔性关节动力学模型,综合有限元法来求杆臂部分的动力学方程,以柔性关节阻尼为设计变量,末端振幅为优化目标,添加变量约束,从而建立关节阻尼的优化模型。借助机械系统仿真软件ADAMS自带算法对机械臂进行优化设计[11],得到最小振幅时的最佳阻尼参数,并将高速和低速模型仿真结果进行分析比较,旨在探究速度对柔性关节的影响。为高速机械臂优化提供理论依据。
1 建立机械臂动力学模型
1.1 柔性关节建模
以Spong模型为基础提出三个合理假设:
(1)弹簧弹性和关节形变成线性关系。比例系数为弹性系数,即柔性关节系统刚度K。
(2)电机质量均匀分布。
(3)转轴与关节中心轴线重合。
故可忽略由质量分布不均和偏心距所引起的转动惯量的影响。柔性关节简化模型如图1所示。在Adams中柔性关节模型如图2所示。

图1 简化后的柔性关节模型
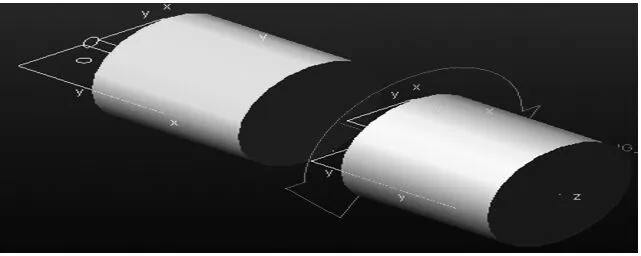
图2 Adams中柔性关节
根据假设可得,经过传感器和减速器等柔性元件传递到关节处的力矩为τi=Ki(θi-qi),qi为第i+1个连杆的转角。将关节阻尼因素考虑进去。综上可建立柔性关节的动力学方程:
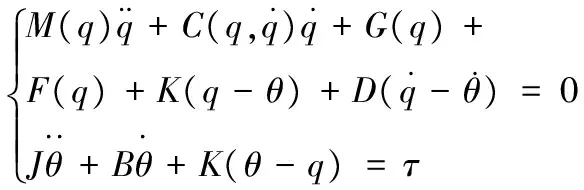
(1)
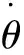

M(q)为机械臂惯量矩阵,M(q)∈Rn;
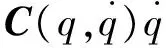
G(q)为重力矢量,G(q)∈Rn;
F(q)为摩擦矩阵,F(q)∈Rn×n;

J表示转动惯量矩阵。K为关节刚度矩阵。B为电机粘性摩擦。τ为机械臂的电机对连杆产生的力矩,τ∈Rn。
1.2 杆臂动力学建模
柔性关节、杆臂和刚体与柔性体耦合部分都是造成机械臂振动不可忽略的因素,为了提高机械臂运动精度和优化分析时得到的数据更加准确,不能忽视其影响。刚体以多刚体动力学建方程。具体运动方程如下:
(2)
m为刚体质量;J′为转动惯量;F为作用在刚体上的外力总和;r为刚体质心位移;ω′为角速度;φr为运动学约束;φπ为驱动约束;λ为拉格朗日矢量;
式(2)中的η为加速度右项;

φq运动学约束的雅克比矩阵;t为时间变量;
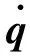
柔体部分借助有限元法和多柔体理论建立方程。具体微分方程如下:
(3)
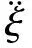
综合多刚体系统动力、多柔体系统动力学理论。把对柔体部分的分析和对刚体的研究方法相结合。机械臂动力学模型由式(1)~式(3)组成。联立微分方程组式(1)~式(3)进行求解,可以求得柔性关节机械臂t时刻末端的位移。
2 建立优化分析模型
为了给考虑柔性关节的机械臂减振,提高机械臂末端执行器运动精度和工作精度,把机械臂柔性关节的阻尼参数作为变量,根据工况选定其取值范围;因为刚柔耦合机械臂的抓取物体的运动过程是一个实时变化的过程,故选取机械臂末端t时刻位移曲线的数值与所提供的理论位移曲线t时刻的数值之差最小为优化目标,建立的目标函数可表示为:
(4)
式中,ΔYt—柔性关节机械臂末端执行器在t时刻的振幅;Yt—柔性关节机械臂末端的仿真位移曲线在t时刻的数值;yt—柔性关节机械臂末端的理论位移曲线在t时刻的数值;ABS()— 机械系统仿真软件ADAMS函数库中的绝对值函数。T为机械臂运动周期;DY()—为实时测量Y方向位移函数。
具体目标函数为:
min(ΔYt)=ABS(DY(Marker_cm-Marker_80))
点Marker_80所在曲线为理论位移曲线。仿真时末端t时刻位移与理论t时刻位移之差可以作为末端振幅,机械臂执行末端理论位移是依据机械臂完成抓取物体的任务的具体工况而预先设定的轨迹位移。把机械臂柔性驱动关节的阻尼系数damp作为设计变量,同时约束范围为damp>0。让目标函数最小化,可得到最优关节阻尼。
3 软件仿真及分析
在建模软件中根据实际工业机器人的尺寸、材料等属性建立机械臂三维模型并对模型进行模块化处理。Ansys适用于有限元分析,Adams适用于刚柔耦合动力学分析,鉴于柔性体对整个机械系统的影响,故通过Adams与Ansys联合仿真,精确地模拟整个系统的运动。在Ansys中生成大臂、小臂、柔性关节三个文件格式为flex.mnf模态中性文件。该文件含有模型的质量和转动惯量信息、频率和振型等参数。在ADAMS的Rigid to Flex模块中将大臂、小臂、柔性关节用三点法导入到ADAMS中,替代同一位置处的刚性体。装配后得到如图3所示的简化的刚柔耦合模型。选取具有代表性的柔性驱动关节-腰关节,将其按照转子扭簧模型进行简化,根据机械臂所要执行抓取任务的工况,在Adams/View的animation controls中跟踪其末端轨迹曲线得到如图4的轨迹。
从工作轨迹可以看出,此过程包含抓取、放下重物、启动、暂停等时刻,这些时刻以及机械臂故障暂停、重物掉落瞬间,柔性关节机械臂末端都会有明显的振动,因此,测量末端的振幅来优化关节阻尼系数的目的就是着重减小这些时刻振动的影响。
在简化柔性关节后的模型上进行仿真分析,设扭簧的刚度系数K为定值。瞬时激振力可以用step函数设置也可以借助Adams中的振动模块设置,在谐响应分析基础上,进行强迫振动分析,在输入通道中将正弦波作为激励参数,在输出通道中将机械臂的末端振动位移作为输出响应,设置激励的频率范围为0~1000Hz。
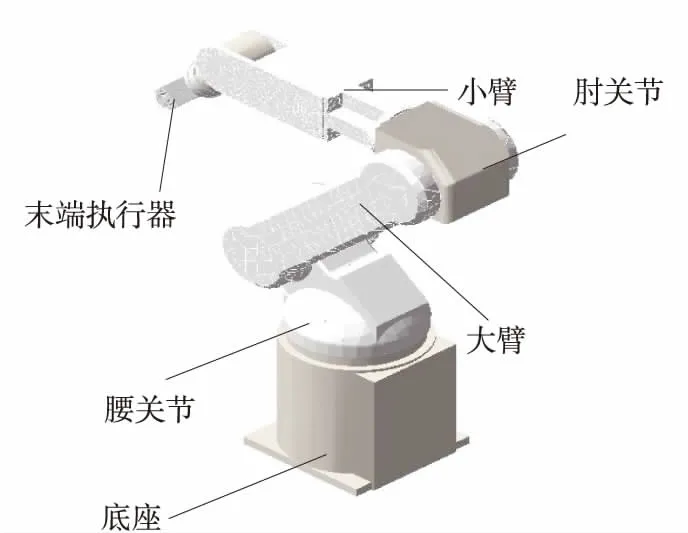
图3 简化后的刚柔耦合机械臂模型

图4 运行轨迹图
仿真优化的步骤:
(1)设柔性关节阻尼变量为damp,类型为实数,单位为阻尼,根据机械臂使用的工况以及材料的考虑阻尼范围在1~200000N·s/mm。
(2)创建强迫振动仿真脚本。
(3)根据柔性关节和振动的关系,借助测量函数FUN创建目标函数,在创建目标函数时选择Adams/view变量和Vibration宏。
(4)在创建的仿真脚本下运行仿真,得到使目标函数最小的最优参数。
(5)改变柔性关节驱动函数再次依照上述步骤进行仿真。驱动函数如表1所示。
(6)分析优化结果。


表1 驱动函数

图5 低速和高速末端振动位移与变量关系图
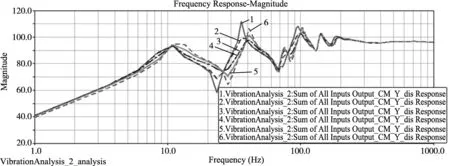
图6 合理阻尼范围内6条不同阻尼末端振动位移响应的幅频曲线
图7是根据Adams的自带OPTDES-GRG算法进行优化[12],按照工况轨迹完成一个周期的仿真的末端振动位移和优化之前的仿真振动位移对比图。自带的广义递减梯度算法,在小位移的情况下,仍然可以保持有效约束。曲线2为优化后的振动曲线。曲线1为优化之前所测的振动位移,从整个运动过程中可以看出,启动时刻振动较大,之后振动衰减,在2.5s左右抓取重物,振幅变大,抓取重物时振幅为11.174mm。将关节阻尼设置为最合理阻尼值后,同样在抓取重物的瞬间,振幅为6.5mm,振幅减小41.17%,柔性关节机械臂在完成启动,抓取,搬运重物,停止工作的过程中,机械臂执行器的末端振动的到了较大的削弱,柔性关节机械臂的运动精度和工作精度提高,对末端振动的抑制减少了重物掉落的概率,提高了执行任务的效率和运动精度。在实际工程应用中,可以采用一些阻尼特性较好的材料,或者在柔性关节中添加阻尼控制器来实现阻尼的调节,还可以通过某些特定结构来实现调节,抑制末端执行器的振动。

图7 振动位移曲线
4 结束语
本文对机械臂的柔性关节和杆件建立动力学模型,探寻阻尼与末端位移关系。使用ADAMS对已建立关节阻尼优化设计模型的刚柔耦合机械臂进行优化设计,对比分析附加强迫振动下机械臂高速和低速两种工况下的结果,得到如下结论:
(1)考虑柔性关节的刚柔耦合机械臂在执行抓取任务过程中,阻尼因素对抑制振动有一定的影响,同为最优阻尼的情况下,高速机械臂比低速机械臂的振幅大。
(2)在优化设计中,把模型的理论应用于仿真之中。在ADAMS/Vibration模块中对考虑柔性关节的刚柔耦合机械臂附加强迫振动,分析了末端振型的抑制。ADAMS/Insight优化设计中得到高速和低速刚柔耦合机械臂末端的振动位移和柔性关节阻尼的关系,取用合理的阻尼参数使得机械臂执行器末端的振动得到较为显著的抑制,提高了减振效率,改善了机械臂动态性能。
(3)对比了机械臂低速和高速两种情况下柔性关节阻尼对末端精度的影响,为设计高速化机械臂控制策略提供了理论依据。
[1] 刘业超,倪风雷,姜力,等.基于关节力矩的柔性关节机器人的控制策略[J].传感器与微系统,2008,27(11):117-120.
[2] 赵杰亮,谷勇霞,阎绍泽,等.谐波传动对柔性机械臂动力学特性的影响[J].清华大学学报,2013,54(4):482-486.
[3] Spong M W. Modeling and control of elastic joint robots [J]. ASME Journal of Dynamic Systems, Measurement and Control, 1987, 109(6): 310-319.
[4] Bahrami M,Rahi A.Tip dynamic response of elastic joint manipulators subjected to a stochastic base excitation [J].JSME InternaI Journal:Series C,2003,46(4):1502-1508.
[5] 陈志勇,陈力.带有柔性补偿的柔性关节空间机器人的增广自适应控制及关节振动抑制[J].宇航学报,2013,34(12):1599-1604.
[6] 陈志勇,陈力.姿态受控柔性关节双臂空间机器人的抗力矩饱和控制与振动抑制[J].工程力学,2016,33(5):227-233.
[7] 郭闯强,倪风雷,孙敬颋,等.具有力矩传感器的柔性关节的振动抑制[J].机器人,2011,33 (4):449-454.
[8] 赵丹青.机器人的柔性关节机械手控制研究[J].计算机仿真,2011,28(2):244-247.
[9] 梁捷,陈力. 柔性空间机械臂末端运动及柔性振动的模糊自适应补偿控制[J].兵工学报,2011,32(1):45-57.
[10] 徐文福,徐超,孟得山.基于粒子群优化的刚柔混合机械臂振动抑制规划[J].控制与决策,2014,29(4):632-638.
[11] 梁永勤,毕凤荣,石纯放.基于遗传算法的麦弗逊悬架参数优化研究[J].机械设计,2017,34(1):15-19.
[12] 庞辉,方宗德,李红艳,等.某载重卡车悬架参数优化及试验研究[J].振动与冲击,2012,31(8):92-95.

