3-RPC分布柔度式柔顺机构结构设计

孙 慧，张荣兴

(1.武汉工程大学 邮电与信息工程学院，武汉 430073；2.江西理工大学 机电工程学院，江西 赣州 341000)

0 引言

精密制造已经成为制造领域的研究热点之一，广泛应用于制造业、建筑业、国防工业、医学等尖端领域。精密定位机构作为精密制造的核心部分，其设计水平的高低将直接影响精密制造的水平。随着科技的发展，在一些超精密定位领域，传统的柔性定位机构已经无法满足精度要求[1-4]，所以设计一种动态特性好、定位精度高以及实用性强的超精密定位机构则显得非常重要。

近几年，定位机构的拓扑优化设计在不断地发展，从当前国内外发展情况来看，现阶段对平面结构的拓扑优化设计研究相对比较成熟，空间三维结构主要集中在构件结构的研究层面，仍处于发展阶段[5]。X. Huang等[6]将改进了BESO优化算法，把优化目标设置为刚度最大化，体积和位移作为优化约束。李枝东等[7]提出导重法，该方法具有求解速度快、优化效果好等优点，解决了优化过程中计算速度慢，求解困难的问题。陈建超[8]等人以载荷路径的遗传算法为基础，为了达到机翼轻量化设计的目标，分别从单一材料和复合材料的角度出发,对机翼进行优化。与成熟的二维结构拓扑优化相比，三维结构的拓扑优化设计还处在发展阶段，具有一定的难度和挑战。

本文在前者研究的基础上，提出一种新型的空间分布柔度式柔顺微定位机构，其不仅具有柔性机构无摩擦磨损、无运动间隙和免装配润滑的优点，还具有并联机构多运动维度、稳定高和承载能力强的特性。利用机构间的输入输出矢量映射关系，并结合拓扑优化方法[9-10]对空间3-RPC型分布柔度式柔顺机构进行拓扑优化设计。得到优化后的三维构型，将拓扑优化后的机构与传统并联机构进行静力学分析和对比，仿真结果表明无论是运动状态还是运动精度，空间分布柔度式柔顺机构比传统的空间并联机构更具有优越性，并对其实体模型进行定位精度实验研究，定量证明了分布柔度式柔顺定位机构设计的合理性及该设计方法的可行性，为空间分布柔度式柔顺机构的优化设计提供了新思路。

1 采用微位移法求解Jacobian矩阵

传统的螺旋理论求得的雅克比矩阵，存在超越方程、非方阵等问题，无法应用于并联机器人的运动学分析。针对3-RPC型并联机器人，提出通过“微位移法”求解微动情况下输入输出之间的位移矢量映射关系，进而得出输入和输出之间4×4的微位移雅克比矩阵。如图1所示，3-RPC 型并联机器人有3个互为对称的支链，各支链的圆柱副C与动平台相联，转动副R与定平台相联，中间是移动副P。定平台坐标系为(o-xyz)，动平台坐标系为(o′-x′y′z′)，y轴、y′轴与A2A3连线平行。定平台与动平台为等边三角形△A1A2A3和△B1B2B3且边长分别为a和b(O和O′为等边三角形的重心)。li表示驱动杆的长度，θi为连杆与下平台之间的倾斜角(其中li=l,θi=θ)。

由螺旋理论可知，3-RPC并联机构的自由度为3，分别是沿X、Y、Z轴移动。假设初始条件定、动平台平行，Ai,Bi分别在定平台坐标系o-xyz和动平台坐标系o′-x′y′z′中的坐标(i=1,2,3)：

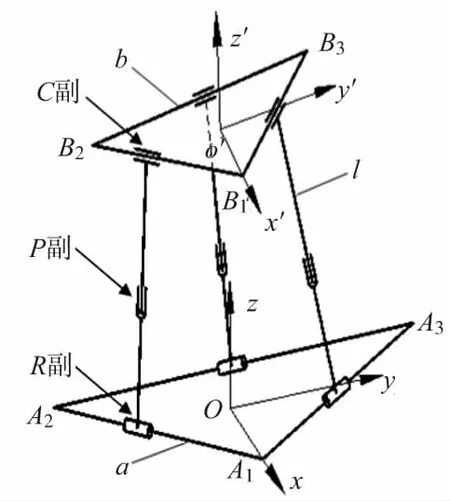
图1 3-RPC并联机构结构简图

假设当压电陶瓷驱动时，动平台坐标系o′-x′y′z′的x′,y′,z′轴相对于定平台转动了γ,β,α以及移动了dx,dy,dz，由坐标系变换原则，可得齐次变换矩阵T。

(1)

式中，Ttrans为平移变换矩阵，Rα,β,γ为旋转变换矩阵，c()=cos(),s()=sin()

基于微位移法所求得的输入输出矢量连续映射关系Jacobian矩阵是非奇异方阵，可以直接用于并联机器人的运动学分析，微位移法的基本思想为：当移动的距离dx,dy,dz和转动的角度α,β,γ趋近于零，那么可得如下等式：

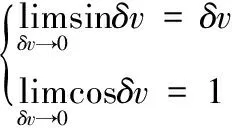
(2)

式中，δv表示α,β,γ,dx,dy,dz及其高阶量。

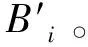
(3)

综上所述：可以求得输入Δli与输出dx,dy,dz之间的关系表达式，其齐次坐标形式如式(4)所示：

MEMS陀螺随机漂移是制约惯性导航精度的关键因素,对MEMS陀螺随机信号进行分析、误差补偿对提高导航精度效果明显[1-3]。陀螺漂移包括了常值漂移和随机漂移[5]。常值漂移可以通过建模补偿,随机漂移可以通过统计分析方法建立陀螺漂移模型,再用Kalman滤波器进行补偿[7-9]。理论上,只有在随机动态系统的结构参数和噪声统计特性参数已知的条件下,标准Kalman滤波才能获得状态的最优估计[4-5]。然而,在实际应用中以上两类参数的获取都或多或少存在一些误差,导致Kalman滤波的精度降低,严重时还可能导致滤波发散[6]。

(4)

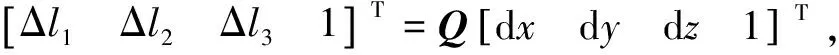
2 3-RPC型定位机构建模

2.1 3-RPC柔性并联定位机构建模

用柔性铰链来替代图1中各支链上的运动副，其中柔性圆柱副C由柔性移动副P和柔性转动副R替代，支链上的移动副和转动副分别由柔性移动副P和柔性转动副R替代，从而得到3-RPC柔性并联机构支链， 3-RPC柔性并联机构模型是由 3 个 RPC 型柔性并联支链对称分布(夹角为120°)，支链中柔性圆柱副C由柔性移动副P和柔性转动副R替代，其中柔性圆柱副C的轴线平行于定平台,且与柔性转动副R的轴线平行,均与柔性移动副P的轴线垂直。各支链输入、输出端分别与定、动平台相连。如图2所示。

2.2 3-RPC分布柔度式柔顺定位机构建模

由螺旋理论可知，空间3-RPC分布柔度式柔顺定位机构有三个输出，分别是沿X、Y、Z轴的移动。基于SIMP材料插值法，建立空间3-RPC分布柔度式柔顺定位机构拓扑优化模型，其中约束条件为体积分数、优化目标为柔度最小，设计变量为密度，数学表达式如下:

(5)

式中，Cx为结构刚度，U为位移矩阵，K为刚度矩阵，u为单元位移矩阵，k单元刚度矩阵，Vx和V分别为拓扑优化后和优化前的体积，v为体积分数，n为离散单元数，xmin为最小密度值，xmax为最大密度值。

3-RPC分布柔度式柔顺机构需要参照同构型的柔性并联机构和微分矢量映射关系式(4)进行建模。由螺旋理论和公式(4)的多输入、多输出映射关系可知，该机构有三个自由度，即沿X、Y、Z轴方向的平移，为了防止冗余驱动和奇异现象的出现，需要保证驱动配置与机构的自由度个数相同。参照全柔性并联机构的驱动配置分布，3-RPC分布柔度式柔顺机构配置三个以 120°夹角对称分布的驱动，在SolidWorks中建立优化初始模型，如图3所示。

图3 3-RPC分布柔度式柔顺机构优化初始模型

将SolidWorks中的3-RPC分布柔度式柔顺机构优化初始模型，另存为IGES格式的文件，并将IGES格式的文件导入Hypermesh软件中进行拓扑优化。首先，定义设计区域、非设计区域，材料选择65Mn(弹簧钢)，赋予模型材料属性(弹性模量E=2.1GPa,泊松比Nu=0.3)；然后，对三维模型进行网格划分(网格为四面体单元，大小为1mm)，设定柔度最小为目标函数，材料体积比为约束条件(体积分数为0.3～0.5)，并根据公式(4)的多输入、多输出映射关系，设置3-RPC分布柔度式柔顺机构拓扑优化工况(对定平台自由度进行约束，使其自由度为0，在模型的三个输入端分别施加1000N的静载荷)；最后，在OptiStruct中经过多次优化迭代，得到拓扑优化后的3-RPC分布柔度式柔顺机构。仿真设计模型如图4所示。图中绿色网格为设计区域，红色网格为非设计区域，凹槽为压电陶瓷驱动装置的安装位置，凹槽中蓝色箭头为加载的驱动力，定平台底部红色箭头为设计约束，驱动力与设计约束共同组成设计工况。

根据拓扑优化设计的工况，在OptiStruct中对3-RPC优化初始模型进行拓扑优化设计，从而得到拓扑优化后的机构构型，如图5所示。

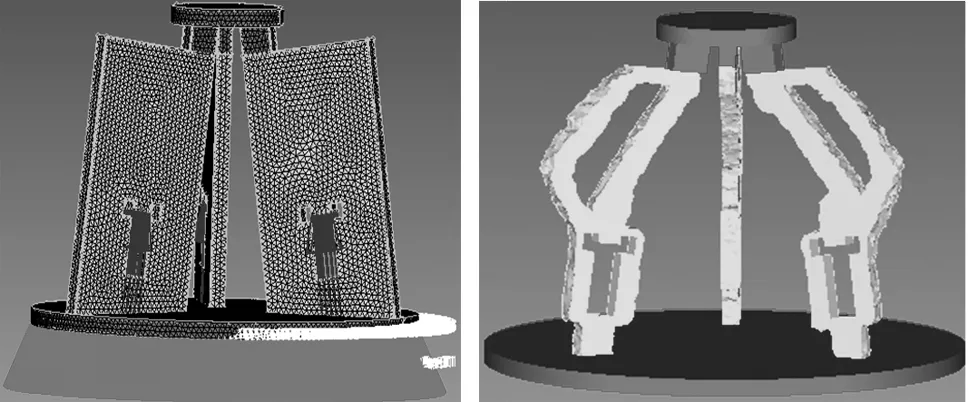
图4 3-RPC分布柔度式柔顺机构仿真设计模型 图5 3-RPC型分布柔度式柔顺机构优化结构

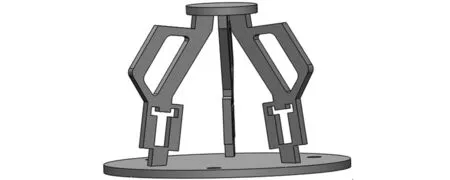
图6 3-RPC分布柔度式柔顺机构模型

3 3-RPC型定位机构静力学分析

3.1 3-RPC型定位机构静力学理论分析

假设初始条件：动、定平台内接三角形边长分别为b=75mm、a=150mm，支链与定平台的夹角φ=75°。

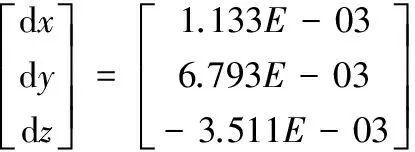
通过仿真可以得出3-RPC型定位机构的三种构型(全柔性、集成式全柔性、分布柔度式)的动平台分别沿X、Y、Z方向的微位移参数及微转动参数，具体仿真如下。

3.2 3-RPC型定位机构静力学仿真分析

首先，通过Solidworks分别建立3-RPC型柔性并联定位机构、分布柔度式柔顺定位机构三维模型，并导入Hyperworks分析软件的optistruct模块中，材料选择65Mn(弹簧钢)，赋予模型材料属性(弹性模量E=2.1GPa,泊松比Nu=0.3)；然后，对三维模型进行网格划分(网格为四面体单元，大小为1mm)，并根据公式(4)的多输入、多输出映射关系，设置工况，对定平台自由度进行约束，使其自由度为0，在模型的输入端分别施加1000N的静载荷。最后，通过Radioss求解器对有限元模型进行静力学仿真分析。将仿真结果导入Hyperview中，分别查看两种不同几何结构的3-RPC型定位机构动平台沿X轴、Y轴、Z轴方向的微运动(微位移及微转动)，仿真结果分别如图7、图8所示。

图7 3-RPC柔性并联机构静力学仿真云图

通过对3-RPC柔性并联定位机构静力学仿真，得到该机构有三个自由度(沿X、Y、Z轴方向的平移)，机构动平台中心点沿X、Y、Z轴三个方向的微位移参数分别为1.483E-03mm、5.940E-03mm、-3.112E-03mm。通过对3-RPC分布柔度式柔顺定位机构静力学仿真，得到该机构有三个自由度(沿X、Y、Z轴方向的平移)，机构动平台中心点沿X、Y、Z轴三个方向的微位移参数分别为1.214E-03mm、6.437E-03mm、-3.312E-03mm。将仿真结果与理论值进行对比，如表1所示。

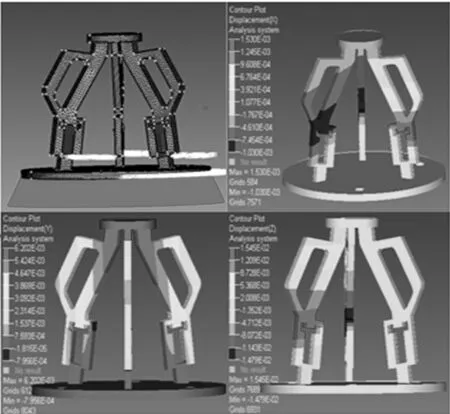
图8 3-RPC分布柔度式柔顺机构静力学仿真云图

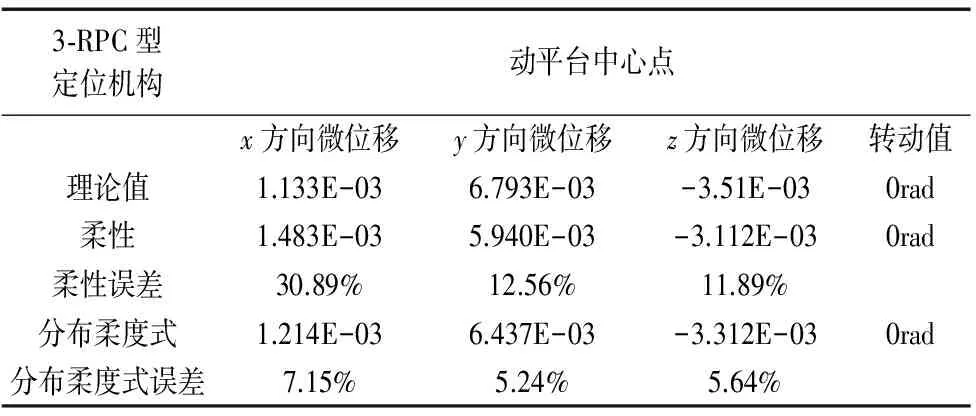
表1 3-RPC型定位机构理论结果与仿真结果 (mm/rad)

对比表1中的理论值和仿真值可知，两种定位机构具有相同的三平移自由度，均能实现沿X、Y、Z轴的微位移，且精度达到了微米级，相较于柔性并联定位机构，3-RPC全柔顺并联定位机构的仿真值更加接近于理论值，误差小。

4 实验研究

首先通过3D打印技术生成3-RPC型分布柔度式柔顺机定位构的三维实体模型，并搭建3-RPC型分布柔度式柔顺定位机构实验系统，如图9所示。在实验过程中，由压电陶瓷控制器来实现对压电陶瓷输出位移的精确控制，通过施加外电场来改变压电陶瓷的极化强度，进而使其自身长度产生变化，提供输出位移。再通过3-RPC型分布柔度式柔顺定位机构来完成力或位移的传递，由英国雷尼绍XL-80型双频激光干涉仪测量其动平台中心的输出位移。为了减小实验误差，需要保证良好的实验环境，避免外界因素的干扰。

图9 实验设备

对机构进行定位精度实验,首先需要对3-RPC分布柔度式柔顺定位机构设定期望输出值，然后通过公式(4)所求得的Jacobian矩阵求得相对于期望输出值的输入位移。由压电陶瓷作为驱动装置，提供输入位移。设置数据采样频率为 5000Hz，来测量3-RPC型分布柔度式柔顺定位机构动平台中心点沿着X、Y、Z轴方向的微位移，3-RPC分布柔度式柔顺定位机构动平台中心沿各轴方向的定位精度实验数据如表2所示。

表2 3-RPC分布柔度式柔顺机构实验结果

由表2可知，实验测量的3-RPC分布柔度式柔顺机构实际位移与理论计算的期望位移值十分接近，误差范围大约在5%以内，验证了3-RPC分布柔度式柔顺机构的有效性。分析误差产生原因，该实验系统由定位机构和多种实验设备共同组成，各组成设备其自身也存在一些引起误差的因素。而且实验系统中动平台中心点的输出位移是该实验系统耦合结果，任何系统中的影响因素都将对实验结果产生影响。

5 结论

本文分析了3-RPC并联机构输入输出之间的矢量连续映射关系，建立该分布柔度式柔顺机构连续映射拓扑优化 S I MP模型，在此基础上对3-RPC分布柔度式柔顺机构进行拓扑优化设计，通过HyperWorks有限元软件对3-RPC型柔性并联定位机构、分布柔度式柔顺定位机构进行静力学分析，并对3-RPC分布柔度式柔顺机构实体模型进行试验研究，得到如下结论：

(1)基于微位移法建立3-RPC型定位机构的微运动矢量映射Jacobian矩阵，无需求解超越方程组，所得到的Jacobian矩阵为非奇异方阵，可以直接作为并联机构仿真系统的理论参考输入值，该求解方法对并联定位机构具有普适性。

(2)与同构性的柔性并联机构相比，通过拓扑优化设计得到的分布柔度式柔顺机构与同构型的传统柔性并联机构具有相同的运动特性且精度更高，误差在允许范围内，验证了基于微运动矢量映射Jacobian矩阵拓扑优化设计方法的有效性, 为空间分布柔度式柔顺机构的优化设计提供了新思路。

[1] 于靖军,毕树生,宗光华.基于伪刚体法的全柔性机构位置分析[J].机械工程学报,2002,38(2)：75-78.

[2] Cynil Quennouelle.Clement GosselinKinematostatic mod-eling of compliant parallel mechanisms[J].Parallel Manipulator, 2011, 46: 155-169.

[3] Kee Bong Choi , Jae Jong Lee ,Gee Hong Kim . A Compliant Parallel Mechanism with Flexure-based Joint Chains for Two Translations[J].International Journal of Precision Engineering and Manufacturing, 2012,13(9):1625-1632.

[4] 叶冬明，李开明.新型三自由度并联机构工作空间分析[J].机械设计与制造，2012,16(2)：199-201.

[5] 中国机械工程学会.中国机械工程技术路线图[M].北京：中国科学技术出版社,2011.

[6] X Huang , Y M Xie. Evolutionary topology optimization of continuumstructures with an additional displacement constraint[J]. Struct Multidisc Optim,2010,40:409-416.

[7] 李枝东, 刘辛军.导重法求解单工况的拓扑优化问题[J].机械工程学报, 2011,47(15):107-114.

[8] 陈建超，张永红，葛文杰,等. 基于多材料组合的柔性机翼前缘拓扑优化[J].机械设计,2011,28(6): 61-66.

[9] Kang Hee,Joe Yong Park,Min Gyu lun ,et al. Reliablity-based topology optimization of elector-Thermal-Complaint Mechan -isms with a New Material MixingMethod[J].International-Journal of Precision EngIneer an Manufacturing, 2012,13(5):693-699.

[10] Li Li, Michael Yu Wang, Peng Wei. XFEMschemes for level set based structural optimization [J]. Frontiers of Mechanical Engineering, 2012, 7(4):335-35.