InSAR时空基线对DEM精度的影响分析

2018-03-07 06:41王之栋唐新明

测绘通报 2018年2期

王之栋，唐新明，李涛

(1. 兰州交通大学，甘肃兰州 730070； 2. 甘肃省地理国情监测工程实验室，甘肃兰州 730070； 3. 国家测绘地理信息局卫星测绘应用中心，北京 100048)

合成孔径雷达干涉(synthetic aperture radar interferometry，InSAR)技术利用同一地区的两景干涉SAR影像得到地表高程信息和形变信息。近年来，InSAR地形测绘技术因其高精度、大范围、全天候、强时效的特点，在地形测绘中得到广泛的关注和研究[1]。影响InSAR地形测绘精度的主要因素有卫星斜距、卫星位置、卫星速度、干涉相位及干涉基线等，其中干涉基线是干涉过程中极为重要的参数[2]。

基线要素包括空间基线、时间基线和多普勒基线，其中空间基线(垂直基线)和时间基线是影响DEM精度较为重要的因素[3]。德国宇航中心的Gerherd Krieger研究表明通过全球定位系统(global positioning system，GPS)载波相位测量并结合高精度轨道模型，空间基线在星上测量精度可以达到1～2 mm[4]。J.H González研究发现，对空间基线的测量进行参数校正后，DEM的测高精度可以达到0.5 m以内[5]。Hanssen通过实验仿真，研究了空间基线对相干性的影响，建立了空间基线去相干与极限基线和垂直基线的关系[6]。Fiedler通过建立空间基线去相干和干涉相位误差的关系模型，分析了空间基线去相关对测高精度的影响[7]。Zebker和Villasenor在假设时间基线去相干仅与散射体的移动有关的前提下，建立了时间基线对相干性影响的近似模型[8]。

本文从InSAR测高原理出发，分别阐述空间基线和时间基线对影像相干性和测高精度的影响，并选用40景天津地区的TerraSAR影像，计算统计780个干涉对的DEM结果，利用航天飞机雷达地形测绘计划(shuttle radar topography mission，SRTM)数据及ICESat-GLAS数据对生产出的DEM结果进行了误差统计；分析空间基线和时间基线对高程RMSE的影响，并统计各基线与影像相干系数的关系，最终总结出时空基线对DEM精度的影响规律。

1 基线要素对相干性和测高精度的影响分析

1.1 空间基线对相干性和测高精度的影响分析

1.1.1 空间基线对相干性的影响分析

对于InSAR地形测绘来说，需要保证整个场景内的散射体都具有较好的相干性，否则会导致巨大的高程误差。相干性表达式为[9]

γtot=γDop·γBas·γSNR·γQua·γAmb·γReg·γVol·γTem

(1)

式中，右边8项分别为多普勒相干性、基线相干性、信噪比相干性、量化相干性、模糊相干性、配准相干性、体散射相干性及时间相干性。在地物类型确定，信噪比、量化、模糊、配准失相干较小的情况下，影像的相干性只与基线相干性、时间相干性相关。空间基线失相干会引起基线相干性的降低，空间基线失相干主要是由主辅雷达观测时的入射角不同而引起的[10]。在成像过程中一般采用零多普勒成像，故空间基线相干性不再受沿航迹基线的影响，此时影响基线相干性的主要是垂直基线的相干性[11]。基线相干性的表达式为

(2)

式中，B⊥为垂直基线；Bcrit为极限基线。极限基线是关于波长λ、入射角θ和地形坡度ζ的函数，其表达式为

Bcrit=λ(BR/c)Rtan(θ-ζ)

(3)

式中，BR为方位向带宽；c为光速；R为斜距。以TerraSAR-X为例，在平坦地形下，斜距R为520 km，入射角θ为30°时，由式(3)可得，其极限基线约为3.4 km。当B⊥为[50，100] m时，由式(2)可得，其基线相干性为[0.970 6，0.985 3]。

1.1.2 空间基线对测高精度的影响分析

一般将空间基线分解为沿轨方向基线，平行于视线方向的基线B‖和垂直于视线方向的基线B⊥。垂直基线与高程之间有非常直观的转换关系，即

(4)

式中，h为观测点的高程；β为本地入射角；φ为观测点的缠绕相位。依据基线转换公式，有

(5)

由式(5)可知，在InSAR对地观测中，为获得较高精度的高程值，空间基线应该在保证高基线相干性的前提下尽可能地长。以TerraSAR-X为例，波长λ=0.03 m，假设斜距R=520 km，入射角θ=30°，则空间基线长度与其带来的测高误差之间的关系如图1所示。在图1中，横轴为空间基线的长度，纵轴为空间基线的长度变化带来的测高误差，结果表明，测高误差会随着空间基线长度的增大呈幂指数倍下降且趋于稳定。

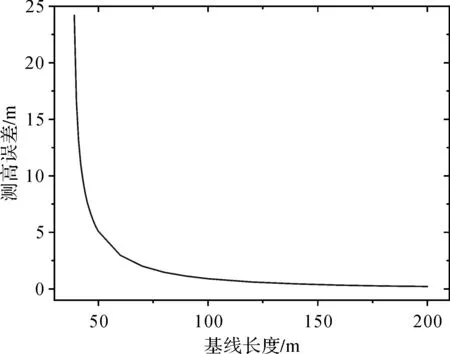
图1 基线长度与基线长度带来的测高误差之间的关系

在对干涉基线误差进行分析时，采用(B⊥,B‖)这种具有明确物理意义的基线分解方式进行分析。

1.1.2.1 平行基线B‖对测高精度的影响

在远场近似的前提下，存在如下关系[12]

B‖=-φ·λ/4π

(6)

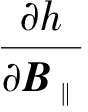
(7)

式中，σB‖为平行基线的测量误差；hamb为高程模糊度。在TerraSAR-X的一景影像中，B‖带来的高程误差与影像幅宽的大小呈正相关，由此带来的高程误差通常在2.3～3.8 mm/km之间变化[14]。因此平行基线带来的高程误差可以简单通过一个常数值c来表示，即

Δh=c

(8)

平行基线带来的误差是沿着视线方向的，即随着斜距的变化，平行基线误差会随着飞行方向发生一定的旋转。对于TerraSAR-X来说，这种旋转带来的高程误差一般在整景内小于4 m，在基线误差小于2 mm时，这部分误差可以忽略不计[3]。

1.1.2.2 垂直基线B⊥对测高精度的影响

目标点高程和解缠后的绝对相位之间存在如下关系

(9)

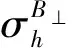
(10)

式中，σB⊥代表垂直基线的测量误差。以TerraSAR-X为例，斜距和入射角分别为520 km和30°，垂直基线测量误差σB⊥为1 cm，高程模糊度为[35，55] m，垂直基线为[122.81，192.99] m。又因为垂直基线带来的高程误差和高程本身相关，由式(10)可知，高程越高，则垂直基线带来的误差也越大，即在同等观测条件下，平地、丘陵、山地、高山地的测高误差会不相同。

1.2 时间基线对相干性和测高精度的影响分析

InSAR的观测原理要求卫星对地面同一片区域进行两次观测[15]。在两次数据获取过程中，当同一分辨单元内的散射体分布或散射体的介电系数发生变化时，则会产生时间去相干和体散射去相干而影响干涉影像对之间的相干性。在干涉测量中，初始观测是由数值确定的相位部分和噪声相位部分组成，即

φt=φbas,t+φscat,t+nt

(11)

式中，φbas,t和φscat,t为数值确定的相位部分，φbas,t为在t时刻卫星基线和地面目标的位置关系产生的相位，其中包含了信号延迟导致的相位；φscat,t为分辨单元内散射体引起的相位，它是关于散射体分布和雷达视角的函数，而时间失相干会引起φscat,t大小的变化；nt为噪声相位。在两次观测中，只有当时间失相干引起的相位φscat,t变化不大时，才可以获取到有效的干涉相位[6]。时间失相干和波长，地物位置有关，在入射角为30°，利用X波段对地物进行观测时，当一个分辨单元内的散射体随机发生1.5 cm的移动时，相干性会降为0.007[8]。

在一个时间周期内，地表可能的变化有很多，因而当前关于时间失相干的分析模型均被证明并非行之有效[6]。一方面，人类的活动会引起地面散射单元的变化，因其不可预测性和不连续性而不能建立准确的数字化模型；另一方面，自然规律的不可抗性也会引起散射单元的变化，如当地表被雪覆盖时，将会出现严重的失相干，而在雪融化时相干性又会提升。经验表明，时间基线控制在1～3 d内，时间去相干是可以被接受的[2]。

2 试验及分析

本文选取了天津地区的40景TerraSAR-X影像进行干涉处理，影像的方位向分辨率为1.9 m，距离向分辨率为1.4 m，地面面积为32.4×56.6 km2。成像时间从2009年4月7日到2010年12月14日，时间间隔为11 d，影像数目为40景，共生成780个干涉对。研究区的地理位置分布如图2所示，图2(a)为研究区域在光学影像上的分布，图2(b)为采用40景影像得到的研究区域平均振幅图。研究过程中对所有的干涉对进行了相同的处理，并输出每一对干涉对的DEM结果，分别利用SRTM数据和高精度激光点ICESat-GLAS数据绘制了DEM误差分布图及DEM误差分布频数图，结果如图3所示。

图2 研究区的地理位置分布

利用SRTM数据和ICESat-GLAS数据作为高程评价参考数据，对780个干涉对生成的DEM的高程进行精度评价，分别计算了各干涉对生成DEM高程的RMSE，结果如图3(a)和图3(b)所示。在图3(a)和图3(b)中，横轴为干涉对的索引值，纵轴分别为利用SRTM数据和ICESat-GLAS数据进行高程精度评价的RMSE。右上角为高程RMSE分布频数图，横轴为高程的RMSE，纵轴为对应的频数，图中只显示了高程RMSE小于1000的干涉对。结果表明，在剔除了高程异常值点后，利用SRTM数据计算得到的RMSE与利用ICESat-GLAS点数据得到的RMSE具有一致性。下文将采用SRTM数据计算得到的RMSE探讨各基线要素对DEM精度的影响。

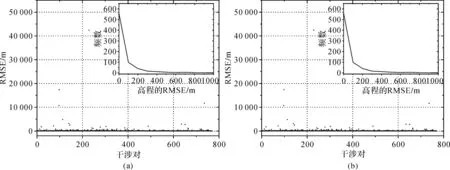
图3 利用SRTM数据和ICESat-GLAS数据进行DEM的精度评价和检核

780对干涉对中，高程RMSE小于6 m的有18对，小于3 m的有0对，即只有2%的干涉对能够满足平原地区1∶10万比例尺地形图测绘的高程精度要求，而所有干涉对都不满足1∶5万比例尺地形图测绘的高程精度要求[16]，这说明重轨干涉SAR数据无法用于地形测绘的业务化应用。本文选取RMSE小于1000的干涉对共762对，统计了空间基线、时间基线、相干性与高程RMSE之间的关系，如图4所示。

图4 高程RMSE与各基线参数的关系

垂直基线由空间基线解算得来，由图4(a)和图4(b)可以看出，空间基线与垂直基线对高程的影响较为一致，即空间基线(垂直基线)越大，高程的RMSE越小。当空间基线(垂直基线)大于100 m时，高程精度较为稳定，高程的RMSE在0～100 m之间变化；而当空间基线(垂直基线)小于100 m时，高程精度稳定性很差，RMSE在0～900 m之间变化。本文取762个干涉对中时间基线小于等于33 d的干涉对87个，并对其垂直基线、空间基线和RMSE进行幂函数拟合，拟合图形如图5所示，其中横轴分别表示垂直基线和空间基线的长度，纵轴均表示高程的RMSE。得到拟合式(12)和式(13)，拟合精度为0.93和0.83。

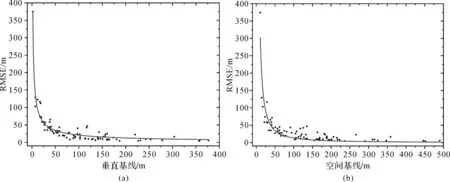
图5 垂直基线、空间基线和高程RMSE的拟合

(12)

RMSE=8 519.1B-1.4

(13)

由上文的分析可知，垂直基线越大高程的RMSE越稳定。当垂直基线大于180 m时，RMSE小于6 m，模糊高小于36.1 m，此时能够确保较高的高程解算精度。为研究时间基线和高程的RMSE之间的关系，在780个干涉对中取垂直基线大于180 m的干涉对38个，对时间基线和高程的RMSE进行线性拟合。线性拟合符合图6中时间基线和高程RMSE之间的关系，拟合图形如图6所示，其中横轴表示时间基线的大小，纵轴表示高程的RMSE。线性拟合精度为0.85，拟合公式如下

RMSE=6.64+0.07t

(14)

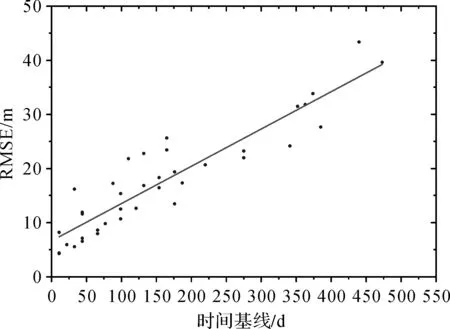
图6 时间基线和高程RMSE的拟合

由图4(d)可得，当相干系数均值小于0.7时，高程的RMSE出现了非常大的波动，变化范围为[0，1000] m。但是当影像的相干系数均值高于0.7时，93.7%干涉对高程的RMSE低于200。因此为避免在对高程进行计算时出现错误的结果，相干系数均值应大于0.7。

图7统计了垂直基线、空间基线、时间基线与相干系数之间的关系。如图7(a)和图7(b)所示，垂直基线和空间基线对相干系数的影响具有一致性，当垂直基线和空间基线小于200 m时，70%干涉对的相干系数位于[0.5，0.7]之间。时间基线对相干系数的影响如图7(c)所示，时间基线越短，相干性越好，反之亦然。时间基线一旦突破200 d后，所有的干涉对的相干性全部低于0.7。

3 结语

本文通过理论分析和试验统计，分析了InSAR测量中空间基线和时间基线对测高精度和相干性的影响。结果表明，空间基线和高程的RMSE呈负相关，大的空间基线可以提高测高的灵敏度，即空间基线在不超过极限基线的前提下越大，系统对高程变化的反应越灵敏。在时间基线不超过33 d的情况下，空间基线与高程RMSE的关系可以用幂函数近似表达。时间基线与高程的RMSE呈正相关，当垂直基线大于180 m时，时间基线与高程的RMSE呈线性相关。影像相干系数的大小会直接影响高程的精度，当相干系数小于0.7时，高程的RMSE在0～1000 m之间变化，此时无法利用影像得到正确的高程信息。相干系数由多个变量共同影响，当垂直基线和空间基线小于200 m时，70%干涉对的相干系数位于[0.5，0.7]之间，当时间基线超过200 d之后，所有的干涉对相干系数全部低于0.7。

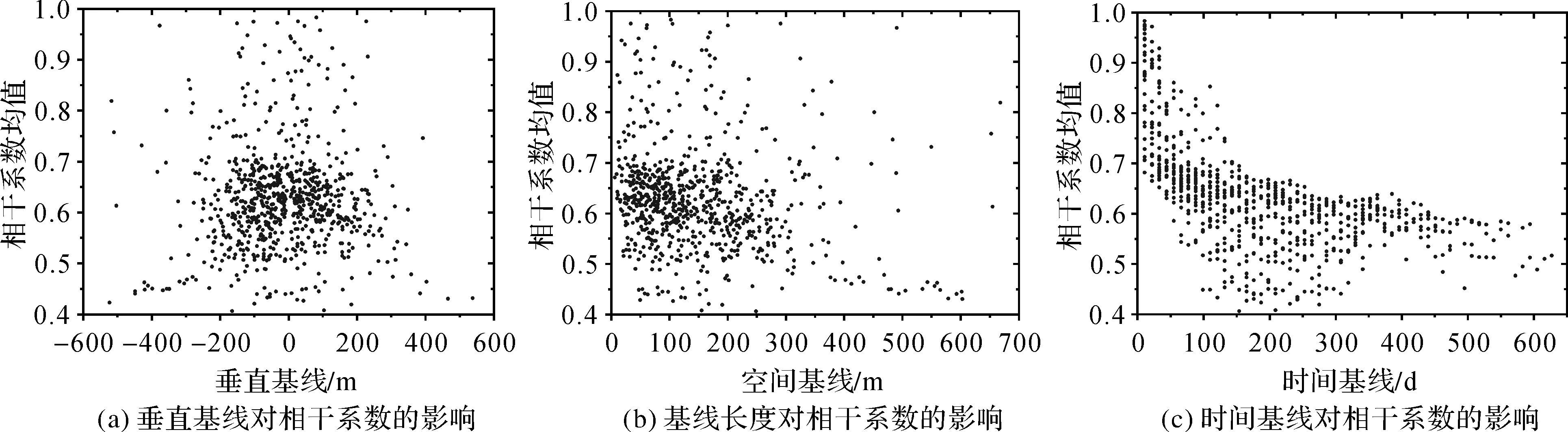
图7 相干系数与各基线参数的关系

[1] KRIEGER G，FIEDLER H，HAJNSEK I，et al.TanDEM-X：Mission Concept and Performance Analysis[C]∥Proceedings of 2005 IEEE International Geoscience and Remote Sensing Symposium.[S.L.]:IEEE，2005:4890-4893.

[2] 李德仁，周月琴，马洪超.卫星雷达干涉测量原理与应用[J].测绘科学，2000，25(1):9-13.

[4] MOREIRA A，KRIEGER G，HAJNSEK I，et al.TanDEM-X：A TerraSAR-X add-on Satellite for Single-pass SAR Interferometry[C]∥Geoscience and Remote Sensing Symposium.Anchorage:IEEE，2004:1000-1003.

[6] HANSSEN R F.Radar Interferometry：Data Interpretation and Error Analysis[M].[S.l.]：Kluwer Academic Publishers，2001:88-90.

[7] FIELDER H，KRIGER G，JOCHIM F.Analysis of Satelite Configuration for Spaceborne SAR Interferometry[C]∥The International Symposium Formation Flying Mission & Technologies.[S.l.]：[s.n.],2002.

[8] ZEBKER H A，VILLASENOR J.Decorrelation in Interferometric Radar Echoes[J].IEEE Transactions on Geoscience and Remote Sensing，1992，30(1):950-959.

[9] MARTONE M，KRIEGER G.Decorrelation Effects in Bistatic TanDEM-X data[C]∥Geoscience and Remote Sensing Symposium (IGARSS).Munich：IEEE,2012:5558-5561.

[10] GATELLI F，GUARNIERI M A，PARIZZI F，et al.The Wavenumber Shift in SAR Interferometry[J].IEEE Transaction on Geoscience and Remote Sensing，1994，32(1):855-865.

[11] KRIEGER G，ZINK M，BACHMANN M，et al.TanDEM-X：A Radar Interferometer with Two Formation-flying Satellites[J].Acta Astronautica，2013，89(8):83-98.

[12] 张永俊.星载分布式InSAR系统的误差分析与DEM精度提高方法研究[D].长沙：国防科学技术大学，2011.

[13] 王超，张红，刘智.星载合成孔径雷达干涉原理[M].北京:科学出版社，2002.

[14] KRIEGER G，MOREIRA A，FIEDLER H，et al.TanDEM-X：A satellite Formation for High-resolution SAR Interferometry[J].IEEE Transactions on Geoscience and Remote Sensing，2007，45(1):3317-3341.

[15] ZEBKER H A，GOLDSTEIN R M.Topographic Mapping from Interferometric Synthetic Aperture Radar Observations[J].Journal of Geophysical Research：Solid Earth，1986，91(1):4993-4999.