GF-1卫星WFV影像几何定位稳定性研究

韩 杰，谢 勇

(1. 许昌学院城乡规划与园林学院，河南 许昌 461000； 2. 南京信息工程大学地理与遥感学院，江苏 南京 210044)

近年来，我国加大了对高分辨率卫星遥感事业的资金和人才投入，突破了一系列的关键技术，成功发射了多颗我国自主研发的高空间分辨率卫星(CBERS-02B、TH-1、ZY1-02C、ZY-3、GF-1、GF-2等)[1]。卫星影像几何定位精度是衡量影像几何质量的一个重要参考指标，众多学者从多方面对国产高分辨率卫星影像几何特性进行了分析。如祝小勇等建立了CBERS-02B卫星影像严格成像几何模型，并利用实测数据对其影像几何定位精度进行评价，分析其几何误差来源[2]。王任享等通过对TH-1卫星影像进行评价后，证明其在无地面控制点辅助的情况下定位精度达到了美国SRTM水平[3]。杨博等在对ZY-02C卫星全色影像的无控定位精度进行分析后，利用嵩山定标场高精度参考数据对ZY-02C卫星全色相机进行在轨几何定标[4]。李德仁利用地面控制点数据对ZY-3卫星前期影像几何定位精度进行评价，发现在无控制点的情况下，其影像直接定位精度优于15 m[5]。黄世存等对GF-1卫星PMS相机的全色和多光谱二级产品几何定位精度进行评价，结果表明其二级产品定位精度满足1∶10万比例尺地形图更新要求[6]。

我国高分对地观测系统的首发星——GF-1卫星搭载的宽覆盖WFV多光谱传感器，采用4台相机拼接成像的方式，能够获取空间分辨率为16 m，幅宽优于800 km的卫星影像，实现了高分辨率与大视场相结合的研制总目标[7]。同样，为了提高该影像定量化应用水平，需要对其影像几何定位精度进行综合评价。虽然相关学者也对此进行了相应探讨，但是上述大多数研究仅仅针对某一时刻获取的影像进行了绝对定位精度的评价。然而GF-1卫星在轨运行已超过4年时间，在此过程中已经获取了大量影像数据，这些数据之间的相对几何定位精度如何，需要作进一步的评价和研究，这对分析影像几何定位稳定性及利用该数据进行遥感定量化时序分析具有重要意义。

本文以北京为例，将ZY-3卫星传感器校正产品作为参考依据，首先分析其单景影像相对几何定位特点；然后对该区域影像相对几何定位精度进行长时间序列评价，分析其定位误差随在轨运行时间变化情况；最后从理论上证明在无严格成像模型的情况下，用户无法利用某一时相影像的有理函数模型(rational function model，RFM)的补偿参数对其他时相影像系统误差进行有效消除。

1 数据介绍

1.1 参考数据的选择

参考数据的选择对评价影像相对几何定位精度具有至关重要的意义。由于本文研究的主要目的是为了评价长时间序列影像的几何相对定位稳定性，因此对参考数据的选择要求有所不同，该数据无需具有非常高的绝对定位精度，只需要保证数据内部几何畸变较小即可。

针对上述对参考数据所需特性分析，结合目前常用的卫星影像数据特点，本文选择ZY-3卫星传感器校正产品作为参考数据。因为该产品实现了CCD片间的无缝拼接，且其自带的有理多项式参数(rational polynomial coefficients，RPCs)具有很高的拟合精度，同时该产品消除了内外畸变参数，并且生产过程中引入的定位误差可以忽略[8]。因此本文选取了2014年1月21日北京地区同一轨道相邻两幅正视传感器校正产品作为参考影像，如图1所示。在对同轨拼接条件检查后发现，所选数据满足影像重叠区域同名点偏差约为一个像素的限制条件，因此可忽略两景影像的相对定位差异[9]。

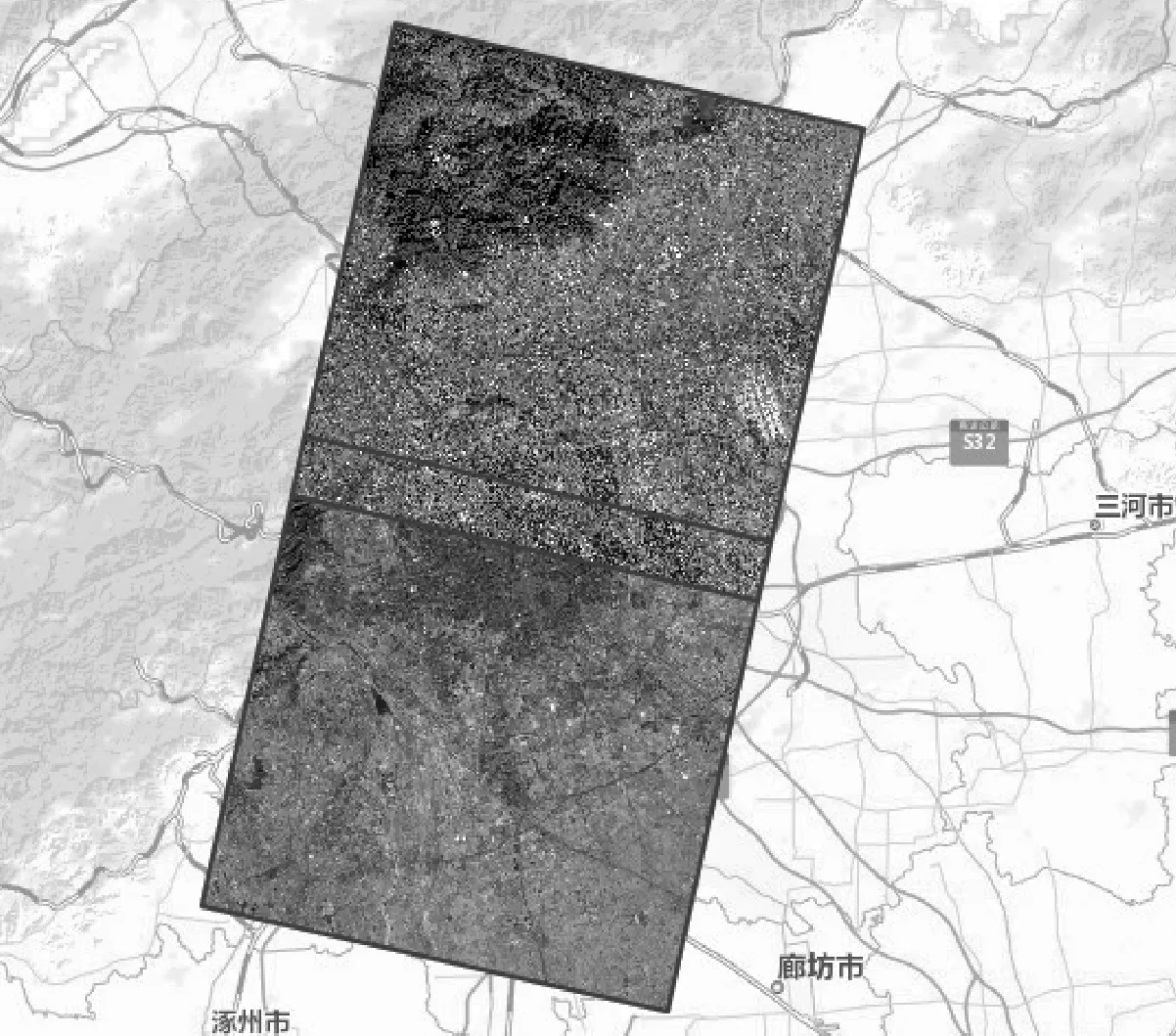
图1 北京ZY-3卫星参考影像覆盖范围

1.2 WFV长时间序列影像收集

本文以北京市区为研究区域，该区域地形以平原为主，其海拔约为50 m。通过数据检索，在去除云层遮盖的影响后，自2013年5月1日至2015年1月23日期间，获取北京地区WFV影像共计53景，其中WFV1影像17景、WFV2影像15景、WFV3影像19景、WFV4影像12景。

2 WFV影像长时间序列相对几何定位精度评价方法

出于对卫星参数信息的保密，普通用户是无法获取严格成像模型参数的，仅能基于影像自带的RPCs参数，采用有理函数模型，实现地物几何信息的提取[10-11]。因此本文以ZY-3卫星影像几何信息为参考，利用RPCs参数及SRTM DEM数据将ZY-3全色影像和WFV影像的同名点坐标投影到物方坐标系中，获取像点经纬度信息，然后将其转换为UTM投影坐标，进而比较物方投影坐标差异，并对WFV影像长时间序列相对几何定位精度进行综合分析。

3 试验结果与分析

长时间序列影像相对几何定位精度分析是通过将待评价的WFV影像集与ZY-3卫星参考影像的同名点进行坐标比对，分析其相对几何定位误差方向及误差大小。因此首先需要利用影像配准方法获取同名点对，但是由于WFV影像与ZY-3影像空间分辨率相差较大，且部分WFV影像与参考影像的成像时间间隔较大，导致部分同名点配准误差较大，因此本文采用人工刺点的方式在每景WFV影像上选取5个同名点进行坐标比较，精度约为1个像素。

3.1 单景影像内部几何定位误差特性

从图2可以看出，与参考影像相比，对于单景WFV影像而言，在小范围区域内(北京城区)，影像内部几何定位误差大小及误差方向表现出了较为明显的一致性。图中箭头长度为误差大小，箭头指向为误差方向。

3.2 WFV影像长时间序列相对几何定位误差分析

通过对大量WFV影像进行试验发现，单景影像内部相对几何定位误差大小及方向均近似，因此本文取每景影像同名点误差大小及方向的均值，对WFV影像几何定位稳定性进行评价。

3.2.1 WFV影像长时间序列相对几何定位误差大小分析

从图3可以看出，对于WFV1和WFV2相机而言，随着卫星在轨运行时间增加，其影像相对定位误差先是逐渐增加，然后趋于稳定的状态，其影像相对定位误差分别稳定在200 m和100 m左右。对于WFV3相机而言，虽然其影像相对定位误差有所波动，但最终稳定在100 m左右。对于WFV4影像而言，出现了个别影像相对定位误差过大的情况，这可能是由于在地面数据处理时，对RPCs参数的生产出现了错误导致的。但是由于影像仅提供了RPCs参数而无严格成像模型参数，因此无法分析产生该误差的具体原因。WFV4影像相对定位误差稳定在100 m左右。

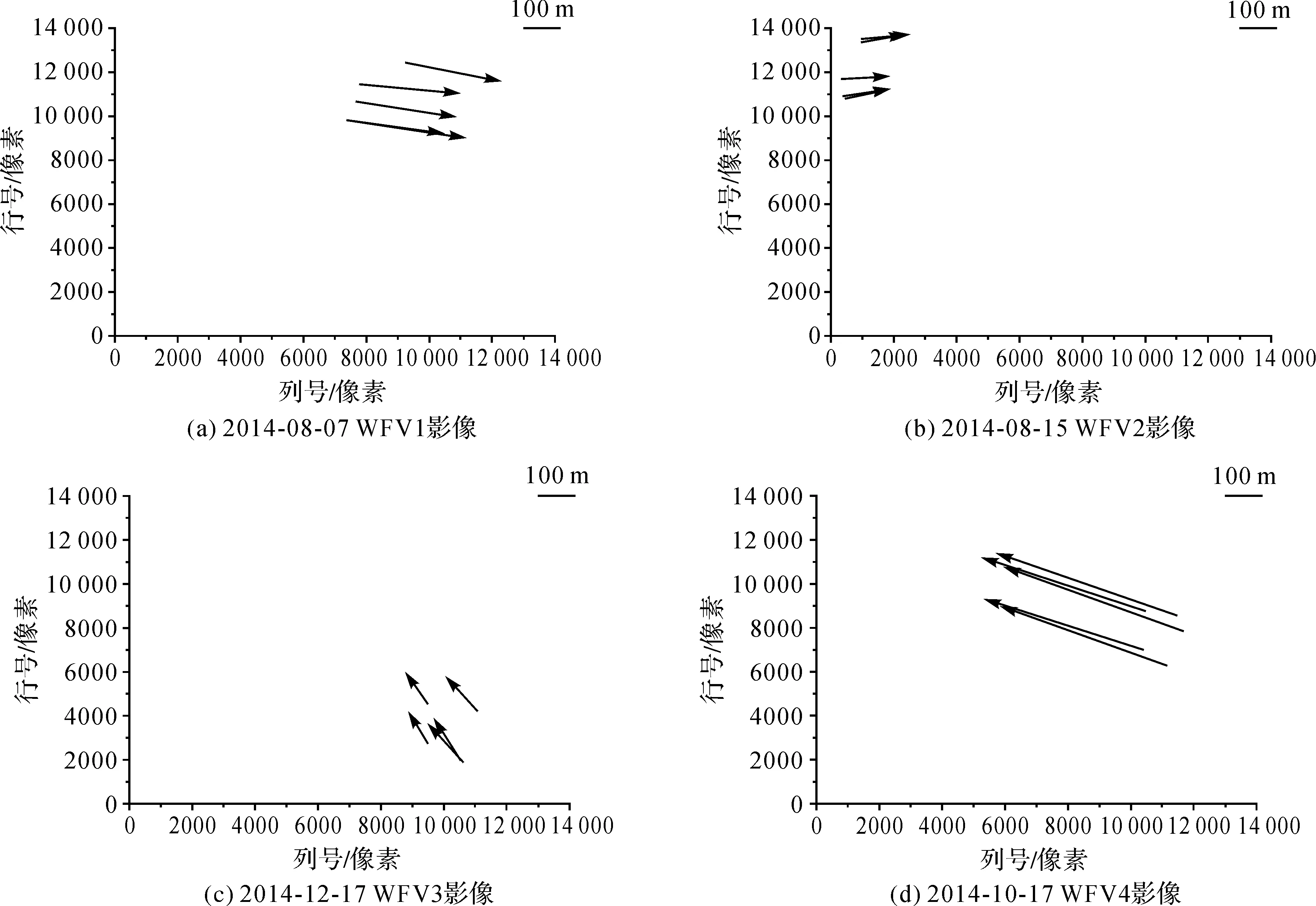
图2 单景影像内部几何定位误差

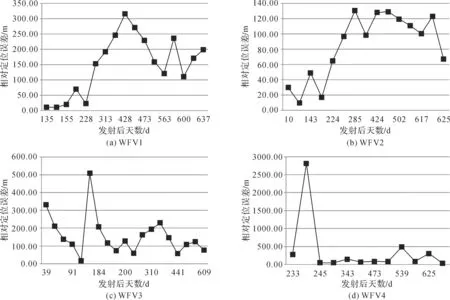
图3 WFV影像相对几何定位误差趋势

3.2.2 WFV影像长时间序列相对几何定位误差方向分析

从图4可以看出，对于不同时相的WFV影像误差方向并无明显的一致性，因此若采用基于像面/物面补偿模型的RFM对影像系统误差进行消除时，利用某一时相的补偿参数是无法有效消除其他时相影像的系统误差的[12]。但是基于严格成像模型对相机进行检校后，可以利用某一时相的检校参数提高其他时相影像定位精度[13-14]。由此可见，虽然RFM对严格成像模型具有极高的拟合精度，但是其通用成像模型的属性还是无法“彻底”取代严格成像模型的优势。其中由于第237天的WFV4影像误差较大，若将其与其他时相误差一同显示，则无法提供较好的目视效果，因此图4(d)中不包括第237天的数据。

为了进一步从理论上证明利用严格成像模型对相机进行检校后，其检校参数可以用来补偿其他时相影像系统误差，而通用成像模型则无法实现的问题。本文从影像成像过程出发对该问题进行分析。众所周知，影响影像直接定位精度的因素主要是卫星定轨/测姿精度和相机安装精度。其中国产卫星定轨精度已经达到厘米级，其对影像直接定位精度的影响可以忽略不计。但是受我国制造工艺及国外禁运的限制，国产卫星平台只能装备精度不甚高的星敏感器进行卫星测姿。相关研究表明，利用测姿设备获取的传感器姿态角通常含有系统误差[13-14]。另外由于卫星在运输及发射过程中，受到外界环境的影响， 相机相对于卫星平台之间的安装参数会发生一定的变化[15]。这种姿态角常差和相机安装误差在直接定位中表现为系统误差，而姿态指向误差和姿态稳定度等误差则表现为随机误差。

如图5所示，H为卫星高度，M为星下点，O为像点理论真值点，OP代表由姿态角常差和相机安装误差引起的系统性定位误差，PQ1、PQ2、PQ3代表姿态角随机误差引起的定位误差，OQ1、OQ2、OQ3则为前两者叠加后的几何综合定位误差。因此，通过图5即可解释WFV相机影像平面定位误差大多位于某半个平面内的原因。这主要是由于系统误差的大小和方向较为固定，而且比随机误差要大得多，因此两者叠加后所表现出来的方向与系统误差方向较为一致。

图5 测姿误差对影像直接定位影响

当用户获取严格成像模型时，可以利用地面控制点对卫星姿态角常差和相机安装误差进行检校，即可消除引起系统误差OP的姿态角常差和相机安装误差，而仅残存几何定位随机误差。利用该检校参数时可以对其他时相影像数据进行误差补偿，提高影像直接定位精度。但是当用户仅能通过RPCs参数对影像进行几何定位时，其只能获取综合的几何定位误差，而无法从中剥离出由姿态角常差和相机安装误差引起的系统误差。因此，利用某一时相的RFM补偿参数无法有效消除其他不同时相影像系统误差。

4 结论与展望

(1) 本文以ZY-3卫星传感器产品为参考，对北京GF-1卫星WFV长时间序列影像进行了相对几何定位稳定性分析与评价，结果表明单景影像内部几何定位误差较为一致，不同时相影像相对几何定位误差并无明显规律。针对该现象，本文从理论上证明了在没有严格成像模型参数时，用户无法利用某一时相影像的RFM补偿参数对其他时相影像系统误差进行有效消除。

(2) 由于本文试验中同名点对的选取是采用人工刺点的方法得到的，这可能会对结果的评价精度产生一定的影响，今后可考虑采用更高精度的影像自动匹配方法，获取大量同名点对信息，从而降低人为的干扰，进一步提高评价结果的准确度。

(3) 由于试验数据有限，本文只在地形较为平坦的地区进行试验，对于地形起伏较大的丘陵或山地区域，其影像几何定位稳定性如何需进一步研究。

致谢：感谢中国资源卫星应用中心为本文研究提供GF-1和ZY-3卫星影像数据。

[1] 韩杰. GF-1卫星影像高精度几何处理方法研究[D]. 北京:中国科学院遥感与数字地球研究所,2015.

[2] 祝小勇，张过，唐新明，等.资源一号 02B 卫星影像几何外检校研究及应用[J]. 地理与地理信息科学,2009,25(3)：16-18.

[3] 王任享，胡莘，王建荣．天绘一号无地面控制点摄影测量[J].测绘学报,2013,42(1)：1-5.

[4] 杨博，王密.资源一号02C卫星全色相机在轨几何定标方法[J].遥感学报,2013,17(5)：1175-1190.

[5] 李德仁.我国第一颗民用三线阵立体测图卫星:资源三号测绘卫星[J].测绘学报,2012,41(3)：317-322.

[6] 黄世存，吴海平，王奇，等. “高分一号”卫星 PMS 图像几何定位精度验证[J].航天返回与遥感,2014,35(5)：81-87.

[7] 陆春玲，王瑞，尹欢.“高分一号”卫星遥感成像特点[J].航天返回与遥感,2014,35(4)：67-73.

[8] 潘红播，张过，唐新明，等. 资源三号测绘卫星传感器校正产品几何模型[J]. 测绘学报,2014,42(4)：516-522.

[9] 张过，汪韬阳，李德仁，等.轨道约束的资源三号标准景影像区域网平差[J].测绘学报,2014,43(11)：1158-1164.

[10] 李国元，胡芬，张重阳，等.WordView-3卫星成像模式介绍及数据质量初步评价[J].测绘通报,2015(S1)：11-16.

[11] GRODECKI J, DIAL G. Block Adjustment of High-resolution Satellite Images Described by Rational Polynomials[J].Photogrammetric Engineering and Remote Sensing, 2003, 69(1)：59-68.

[12] TONG X H, LIU S J, WENG Q H. Bias-corrected Rational Polynomial Coefficients for High Accuracy Geo-positioning of QuickBird Stereo Imagery[J].Photogrammetry and Remote Sensing, 2010, 65(2)：218-226.

[13] 袁修孝，余俊鹏. 高分辨率卫星遥感影像的姿态角常差检校[J].测绘学报,2008,37(1)：36-41.

[14] 袁修孝，余翔.高分辨率卫星遥感影像姿态角系统误差检校[J].测绘学报,2012,41(3)：385-392.

[15] 贾博，姜挺，江刚武，等.基于偏移矩阵检校的SPOT-5遥感影像高精度直接定位[J].测绘科学技术学报,2012,29(5)：368-372.