大尺度泄爆构件对室内爆燃压力影响的实验研究

孙 松，王明洋，高康华，赵天辉，郭 强

(陆军工程大学爆炸冲击防灾减灾国家重点实验室，江苏 南京 210007)

随着甲烷、乙烯等可燃气体在生产生活中的广泛应用，设备老化、操作失误等原因引起的气体爆炸事故频繁发生，给人们的生产生活造成了巨大危害，因此对燃气爆炸的研究与防治已经成为当今社会亟待解决的问题。由于室内爆燃压力通常呈现出升压时间长、峰值压力小的特点[1-2]，因此可将受限空间内的爆炸超压简化为准静态压力[3]，此时在建筑结构上安装泄爆构件可以有效降低屋室内的爆炸超压，达到保护结构的目的[4]。

针对泄爆构件对于爆室内压力的影响，学者们进行了大量实验并推导出相应的理论模型。Cooper等[5]在长方体容器内进行燃气泄爆实验，得到爆燃气体泄放过程中较为典型的压力时程曲线，如图1所示。分析认为P1点处为泄爆压力，此时泄爆构件开启，压力下降；随后火焰传播至容器外部引起泄放的未燃气体燃烧爆炸，阻止内部气体泄放，使得屋室内压力上升达到P2点；当火焰体积达到最大时，室内压力达到峰值P3；燃烧结束后，火焰遇壁面反射，产生声波不稳定现象，使室内出现压力峰值P4点。胡俊等[6]在柱形容器中进行泄爆实验，研究了不同泄爆压力与泄爆面积对于容器内压力的影响；Bao等[7]通过在12 m3的屋室内对不同浓度下泄爆构件对于大尺度空间内泄放压力与声波震荡效应的影响进行了实验研究；Moen等[8]根据气体状态方程、等熵压缩方程、守恒方程结合火焰传播物理模型推导出气体爆炸压力计算的理论模型。

现有的研究大多集中在泄爆窗、泄爆口等小尺度泄爆构件上，其相对泄爆面积(AV/V02/3，AV为泄爆面积，V0为腔体体积)不超过30%，但在实际生活中时常使用泄爆板、泄爆墙等大尺度泄爆构件对燃气爆炸灾害进行防护，对于这种大尺度泄爆构件的研究现在相对较少。本文中，在自行设计的气体爆炸发生容器中进行实验，分析大尺度泄爆条件下爆燃压力的产生机理及变化特点，探讨不同气体浓度条件下泄爆条件对于内部爆燃压力的影响；将实验结果与前人理论模型进行对比，定量描述泄放引起的火焰湍流加速作用对于内部爆燃压力的影响。

1 泄爆实验

1.1 实验装置

实验在自制的大尺度泄爆实验装置中进行，图2给出了装置示意图。装置主体为一端封闭一端开口的爆炸容器，在开口端安装尺寸为1.2 m×0.6 m的泄爆构件组成密闭空间。实验中选用乙烯作为可燃气体，在爆炸腔体侧面等距离设置进气孔与抽气孔，并运用压力分配法配气，气体的泄放由气瓶上的减压阀与进气管上的球阀控制，通过流量计与压力表实现体积分数的调控。容器另一端中部通过法兰结构与电阻丝点火器连接构成点火系统，其最高点火温度为500 ℃。

实验选用硅酸钙板制成2种规格的泄爆构件(以下称为B1和B2)，静载作用下分别在7与13 kPa时破坏，并以此作为各自的开启静压；在爆炸容器顶部安装PCB113B26系列压电式高频压力传感器，用于测试内部爆炸压力；在泄爆构件背爆面粘贴应变片，记录泄爆构件的断裂时间，并将该时刻相应的室内压力作为泄爆构件的击穿压力；数据采集系统将采集到的电信号转化为压力信号并输出，数据采样频率为200 kHz。高速摄影仪置于距泄爆口侧面8 m处，拍照频率为1 000帧/s。实验流程如图3所示，相同条件下每组实验进行3次以保证实验结果的可重复性。

1.2 实验结果

根据各传感器测得的压力数据绘制压力时程曲线。图4给出了乙烯体积分数为4%时泄爆构件B2泄爆过程中各传感器测得的原始压力时程曲线，其中压力传感器1靠近点火端，传感器3靠近泄爆口，如图2所示。

实验中发现各测试点测得的数据均如图4所示，每组实验中3个测点所测压力时程曲线基本相同，即腔体内压力均表现为准静态压力。分析其原因：因为实验腔体内部空间较小，此时火焰发展受限，未经充分加速，传播速度较慢，产生的前驱冲击波较弱，可以近似看成高速传播的声波；同时由于在较小的有限容积内压力传播距离较短，升压过程中压力波遇器壁反复传播多次，故可以认为压力均匀，此时容器内压力可看成准静态压力，各传感器测得的压力曲线基本相同[3,9]。为了便于分析，在下文中取各测点平均值作为腔体的内部压力进行分析。

由于乙烯体积分数不同、泄爆板的泄爆压力不同，实验中共测得3种典型的压力时程曲线，通过100 Hz低通滤波对所得曲线进行处理后的结果如图5所示，不同体积分数(η)下腔体内的压力时程曲线类型如表1所示。

泄压板类型曲线类型η=4η=5η=6η=7η=8η=11B1AAABBCB2AABBB/CC

2 分 析

2.1 体积分数对泄爆结构击穿压力的影响

通过泄爆板上应变片断裂瞬间室内的压力值测试2种泄爆板在不同乙烯体积分数下的实际击穿压力，如图6所示。实验发现当乙烯体积分数小于7%～8%时，泄爆板的击穿压力随体积分数增加而增加；当乙烯体积分数大于7%～8%时，泄爆板的击穿压力随体积分数增大而减小，且在实验中发现两种板在不同体积分数下的击穿压力均大于静载作用下测得的泄爆压力。分析原因认为当乙烯体积分数为7%～8%时化学反应最剧烈，此时压力上升速率较快，爆炸动载对泄爆结构的动力效应使得实际击穿压力大于开启静压。随着气体体积分数偏离最佳反应体积分数，压力上升速率下降，泄爆结构上的荷载作用时间增长，击穿压力逐渐趋近于开启静压。

在实际工程事故中泄爆构件所承受的气体爆炸荷载升压时间受多种因素影响，因此忽视体积分数对升压时间的影响，认为不同体积分数下泄爆构件破坏时对应的室内压力均等于开启静压会与实际情况产生较大误差，影响安全泄放设计。

2.2 低体积分数条件下压力变化情况

当乙烯体积分数小于6%时，实验测得腔体内压力变化曲线为图5中的A类型。现以泄爆构件B2在体积分数为5%时的时程曲线进行分析，压力时程曲线如图7所示，图中虚线表示应变片断裂时刻。通过实验发现低体积分数条件下泄爆板击穿后压力不会马上出现明显下降，而是出现一个平台期。分析认为，泄爆板被击穿开始泄压后，腔体内的压力由泄放的压力与腔体内乙烯继续燃烧产生的压力共同决定。乙烯在低体积分数条件下反应强度较小，而泄爆板、泄爆墙等大尺度泄爆构件的开启往往需要一个过程，当乙烯体积分数较低时其开启过程较为缓慢，如图8所示。图8为高速摄影得到的泄爆板开启过程，左上角编号与图7压力时程曲线上的标注点相对应，表示同一时刻。从图中发现此时泄爆板从出现裂缝到完全开启需要数十毫秒，因此虽然泄爆构件尺寸较大，但在应变片断裂时刻泄爆面积较小，泄放的压力与燃烧产生的压力基本持平，室内压力曲线出现平台期。随着反应进行泄放的未燃气体会对腔体内火焰产生扰动，增加其湍流度，火焰与未燃气体接触面积增加使乙烯反应更加剧烈；同时火焰由泄爆口流出，点燃泄放的未燃气体，阻止内部气体泄放，此阶段泄放压力小于乙烯继续反应产生的压力，腔体内压力继续上升出现峰值P1。

2.3 最佳反应体积分数条件下压力变化情况

当乙烯体积分数处于反应最佳体积分数附近时压力曲线出现双峰值。图9为泄爆构件B2在乙烯体积分数为7%时的压力时程曲线。对照高速摄影发现最佳体积分数条件下乙烯反应剧烈，此时泄爆板开启过程较快，可近似认为应变片断裂瞬间泄爆板完全开启，此时泄放压力大于腔体内反应产生的压力，泄爆板开启后出现明显的压力下降。将该工况与低体积分数条件下屋室内压力变化情况对比发现，泄爆构件的开启时间会对腔体压力变化产生重要影响，因此在泄爆设计时应对泄爆构件的开启方式与开启时间加以考虑。

泄爆板开启后腔体内未燃气体泄漏，压力下降，出现峰值P1；泄放的未燃气体同时会增加腔体内火焰传播的湍流度，加快反应速率，当火焰传出腔体点燃泄放的未燃气体又会使得腔体内压力上升，出现峰值P2[10]，该条件下腔体内的压力变化情况及机理与图1所示的小口泄放条件下压力变化情况相似。

2.4 高体积分数条件下压力变化情况

当乙烯体积分数大于8%时，实验测得腔体内压力变化曲线为图5中的C类型。实验发现腔体内压力值会由峰值压力衰减为负压，随后再次上升，达到第二个峰，高速摄影拍摄到火焰发展情况如图10所示。

由高速摄影拍摄到的图像可以观察到腔体口部的反应过程：在泄爆板击穿后火焰马上从击穿孔洞传播至腔体外部，此时泄爆板全部被击穿，大量燃烧产物外泄，在150 ms时泄放口部燃烧现象最为剧烈。大量气体外泄造成腔体内压力急剧下降出现负压区，此时泄爆口外部空气进入腔体与腔体内未反应乙烯气体混合，如图10所示在197 ms时发生二次爆炸，引起腔体内压力再次上升。

与小口泄放相比，大尺度泄爆可能会引起外部空气回流进入密闭空间发生二次爆炸，对结构造成二次破坏，因此在泄爆防护设计中，不能为了提高泄压效果而盲目增加泄压面积，必须考虑二次爆炸的影响合理确定泄压面积。

3 常用压力计算模型在长方体容器大尺度泄放条件下的应用

目前在泄爆条件下受限空间内的压力计算方面，已经有较为成熟的理论[11]，其中李克山模型应用最为广泛，但该模型现在一般被使用在球形或柱形容器小口泄放中心点火的情况，对于长方体容器大口泄放的计算该模型很少涉及。由于该模型假设一旦达到泄爆压力泄压构件立即开启，与实验中最佳反应体积分数下的开启状况较为相似，因此，本文中针对最佳体积分数条件，结合实验工况对李克山模型[12-13]进行修正并运用计算机编程对其进行数值求解，并通过将计算值与实验值对比，来验证李克山模型在长方体容器大尺度泄放条件下的适用性。

乙烯气体在腔体内燃烧时遵循以下基本方程：

式中：p为压力；V为体积；n为气体物质的量；R为理想气体常数；T为热力学温度；h为气体热焓，h=γpV/(γ-1)；v为气体流动速度；Ku与Kb分别为未燃气体与已燃气体的等熵压缩系数，γu为未燃气体绝热指数，γb为已燃气体绝热指数。

通过以上基本方程结合火焰传播的物理过程，可以推导出已燃气体质量分数wb、燃烧距离x、压力p、未燃气体泄放质量分数wu与时间t的微分关系，控制方程为：

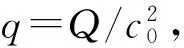
计算模型中，认为火焰内部均为已燃气体，因此火焰体积与已燃气体体积相等。对于火焰的传播形状，由高速摄影观察到最佳体积分数下火焰由泄爆端流出时其阵面可近似认为是平面，故为计算简便假设火焰未接触侧壁时为球形传播，接触侧壁时为平面传播，则端部点火时火焰的表面积与体积表达式为：

(9)

式中：2a、2b、2c为爆炸腔体的长、宽、高，x为火焰半径。

根据Paolo对大量实验分析拟合得到的公式[14]，可计算火焰传播速度：

(10)

式中：u0为基本燃烧速度；经验系数α=2，β=-0.25；φ1为自湍流系数；φ2为泄放引起的湍流作用系数。

可燃气/空气混合物的爆热Q可根据盖斯定律[15]由下式计算：

Q=H2-H1=∑njhj-∑nihi

(11)

式中：Q、H2、H1分别是爆热、产物总焓和反应物总焓；i表示反应物，j表示生成物。

根据火焰在腔体内的几何特点与物理状态得到由偏微分方程组组成的控制方程，通过四阶龙格库塔法对偏微分方程组进行数值求解得到压力时程曲线并与实验值进行比较，结果如图11所示。可以看出实验值与计算值吻合较好，李克山模型在长方体容器大尺度泄爆构件条件下仍具有较好的适用性。

4 结 论

(1) 由于密闭空间内燃气爆炸升压时间较短，爆炸动载对泄爆结构的动力效应明显使得其实际击穿压力大于开启静压，且气体体积分数越接近最佳体积分数泄爆结构的实际击穿压力越大。因此，不同体积分数下泄爆构件破坏时对应的内部压力均等于开启静压会与实际情况产生较大误差，影响安全泄放设计。

(2) 实验发现泄爆构件并非达到泄爆压力马上开启，其开启需要一个过程且构件开启时间会对容器内的压力变化产生重要影响，因此在泄爆防护设计中需要考虑泄爆结构的开启时间与开启方式对泄爆效果的影响；当开启时间仅为数毫秒时可认为构件达到泄爆压力马上开启，此时李克山模型在长方体容器大尺度泄爆条件下仍具有较好适用性。

(3) 火焰由大尺度泄爆构件的击穿孔洞传播至外部空间时会在阵面后方形成负压区，腔体内可燃气体体积分数较高时外部空气因负压区存在由泄爆孔洞进入腔体可能与未燃气体再次反应发生二次爆炸，因此在泄爆设计中不能盲目增加泄爆面积以防止二次爆炸对结构造成破坏。

[1] MOLKOV V, DOBASHI R, SUZUKI M, et al. Modeling of vented hydrogen-air deflagrations and correlations for vent sizing[J]. Journal of Loss Prevention in the Process Industries, 1999,12(2):147-156.

[2] SUSTEK J, JANOVSKY B. Comparison of empirical and semi-empirical equations for vented gas explosion with experimental data[J]. Journal of Loss Prevention in the Process Industries, 2013,26(6):1549-1557.

[3] SHEARER M J, TAM V H Y, CORR B. Analysis of results from large scale hydrocarbon gas explosion[J]. Journal of Loss Prevention in the Process Indestries, 2000,13(2):167-173.

[4] HAN Yongli, CHEN Longzhu. Mechanical model of domestic gas explosion load[J]. Transactions of Tianjin University, 2008,14(6):434-440.

[5] COOPER M G, FAIRWEATHER M, TITE J P. On the mechanisms of pressure generation in vented explosions[J]. Combustion and Flame, 1986,65(1):1-14.

[6] 胡俊,浦以康,万士昕.柱形容器开口泄爆过程中压力发展特性的实验研究[J].爆炸与冲击,2001,21(1):47-52.

HU Jun, PU Yikang, WAN Shixin. Experimental investigations of pressure development during explosion vent from cylindrical vessels[J]. Explosion and Shock Waves, 2001,21(1):47-52.

[7] BAO Qi, FANG Qin, ZHANG Yadong, et al. Effects of gas concentration and venting pressure on overpressure transients during vented explosion of methane-air mixtures[J]. Fuel, 2016,175:40-48.

[8] MOEN I O, LEE J H S, HJERTAGER B H, et al. Pressure develpoment due to turbulent flame propagation in large-scale methane-air explosions[J]. Combustion and Flame, 1982,47(82):31-52.

[9] BAUWENS C R, CHAFFEE J, DOROFEEV S B. Vented explosion overpressures from combustion of hydrogen and hydrocarbon mixtures[J]. International Journal of Hydrogen Energy, 2011,36(3):2329-2336.

[10] CHOW S K, CLEAVER R P, FAIRWEATHER M, et al. An experimental study of vented explosions in a 3∶1 aspect ratio cylindrical vessel[J]. Institution of Chemical Engineers, 2000,78(6):425-433.

[11] 赵衡阳.气体和粉尘爆炸原理[M].北京:北京理工大学出版社,1996:208-214.

[12] 毕明树.气体和粉尘爆炸防治工程学[M].北京:化学工业出版社,2012:129-131.

[13] 孙敖.建筑物内可燃气体爆炸泄放研究[D].南京:解放军理工大学,2013.

[14] PAOLO C, ROTA R, CARR S, et al. Vented gas deflagration: A detailed mathematical model tuned on a large set of experimental data[J]. Combustion and Flame, 1990,80(1):49-64.

[15] 张奇,白春华,梁慧敏.燃烧与爆炸基础[M].北京:北京理工大学出版社,2007:41-42.