央行持有国债变化对利率期限结构的影响
——基于美国数据的实证分析
张雪莹 刘梦
(山东财经大学金融学院,山东济南250014)
一、引言及文献综述
2008年金融危机的爆发使得西方主要发达国家采取非常规货币政策以刺激经济。美联储通过直接在国债交易市场上增加对中长期国债的购买数量来压低国债中长期利率。伴随着购债计划的推进,美联储资产负债表资产端规模也迅速扩大,从2008年初的近9000亿美元迅速增长至2014年10月的4.5万亿美元,体量约占美国国民生产总值的24%①,远远超过了宏观环境稳定时6%左右的一般水平②。图1显示,截至2014年10月美联储宣布退出量化宽松政策时,美联储持有美国国债和抵押支持证券(MBS)总额分别达到了2.46万亿美元和1.72万亿美元的历史高位,并在近年来维持这一水平。
从2015年底开始,美国经济回暖迹象显现,2017年3月失业率降到4.5%的历史低位,接近自然失业率的水平,核心通胀率也已经接近2%的目标③。伴随着美国经济复苏,美联储开始考虑逐步缩减资产负债表的规模。在联邦公开市场委员会(FOMC)3月中旬召开的会议中,美联储官员对资产负债表规模正常化议题进行了讨论,并认为2017年晚些时候进行缩表“可能是合适的”。根据纽约联储的报告,“到2021年底,美联储目前规模约4.5万亿美元的资产负债表可能被缩减至略低于3万亿美元的水平”。由于美联储所持有的抵押支持证券(MBS)大部分剩余期限都在10年以上,而国债到期期限则相对较短,未来5年内到期的规模占到了美联储持有国债总规模的近60%,根据渐进式缩表进程的安排预期,在缩表前期,美联储有可能倾向于逐渐缩减到期国债的再投资规模,而后期可能会逐步停止到期国债的再投资进程并卖出未到期的国债和抵押支持证券(MBS),进而使美联储资产负债表资产端规模逐渐恢复到正常水平。可见,美联储缩表的进程将导致其持有国债水平的变化。在这一背景下,研究美联储持有国债规模的变化对于市场利率水平及其他宏观经济变量有何影响,具有重要的理论价值和政策意义。
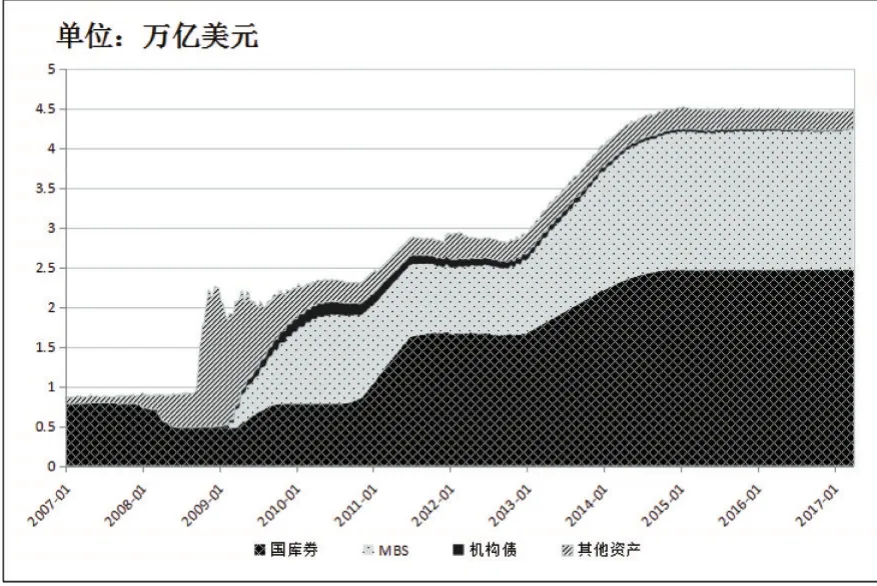
图1:美联储资产负债表资产端构成
值得注意的是,尽管美联储持有国债规模自2008年以来持续增加,在2014年10月退出量化宽松后也一直保持在2.46万亿美元左右的高位,但美国的赤字财政政策使得近些年来美国国债总额出现较大幅度的增长,2008—2016年间,美国联邦债务占GDP的比例由64.34%上升到105.87%,国债总量从2008年10月的10.63万亿美元增加到2017年2月的19.92万亿美元,这使得美联储持有国债占国债总额的比例在美联储启动缩表政策之前已经呈现出波浪形的变化(见图2)。这也使得我们可以基于美联储持有国债比例变化的历史数据,研究其与市场利率及重要宏观经济变量的关系,进而对分析美联储缩表行为的影响提供借鉴。
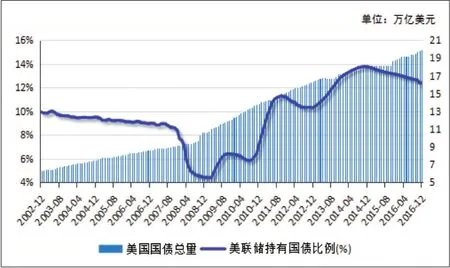
图2:美联储持有政府债务情况
关于央行持有国债变化对利率期限结构的影响,一些学者进行了细致的分析。例如,Hamilton和Wu(2011)在对美国第二轮QE的研究中发现,美联储高达4000亿美元的国债购买计划使10年期国债利率下降了14个基点。Chadha等(2014)考察了2009年3月到2010年11月间英国央行购买政府债券政策对该国名义和实际国债利率期限结构的影响。结果显示:政策实施后,10年期国债名义利率平均下降46个基点;但并未对实际远期利率产生显著影响。Kaminska等(2014)的研究表明:美联储2008—2012年间推行的大规模资产购买计划使美国10年期国债收益率下降近140个基点。邓晓兰等(2014)基于美国2009—2013年间的数据研究表明:美联储的大规模购债行为具有内生性,在长期中并没有起到降低利率的作用,短期内对利率的冲击具有不确定性和不可持续性。Eser和Schwaab(2016)运用事件研究法,以欧元区10个国家的5年期国债收益率为标的研究了欧洲央行2008年10月至2011年12月间施行的非常规货币政策的宣告效应,并在此基础上构建由希腊、西班牙、爱尔兰、意大利和葡萄牙5国面板数据构成的模型。结果显示,样本国家国债购买量每增加国债流通总额的1‰,能够降低该国5年期国债收益率近3个基点。
通过对已有文献的梳理能够发现,现有文献在研究央行持有国债比例对利率有何影响时,所用的实证计量方法较为简单;且仅考察了该政策对某些关键期限利率的影响,这样只能利用某些特定期限利率的信息,而忽视了大量其他期限的利率信息。为此,本文使用美国2008—2016年的数据,在Diebold、Rudebusch和Aruoba(2006)提出的DRA模型基础上,引入央行持有国债的比例,分析利率期限结构、宏观变量和央行持有国债比例之间的动态交互关系。DRA模型不仅能够避免因仅对关键利率进行考察而受某些期限利率异常值的影响,而且能够刻画整个利率期限结构曲线随时间变化的动态规律。另外,DRA模型所使用的因子载荷更符合经济意义,在模型构造和估计方面也具有更大的灵活性。本文余下部分安排如下:第二部分为数据说明和计量方法,第三部分为检验结果和分析,第四部分为总结及政策意义。
二、数据和计量方法
(一)数据
本文使用2008年1月至2016年12月的月度数据,共108个月。图2显示,2008年全球金融危机爆发后,美联储持有的美国国债面值占市场流通美国国债总额的比例大幅提高。因此本文选用2008年1月之后的数据进行研究。其中,美国国债利率使用期限为12、24、36、60、84、120、240、360个月的财政部发行的国库券即期收益率数据。宏观经济变量中,经济增长率gt用美国实际GDP同比增长率代表,gt=ln(GDPt/GDPt-12),其中GDP数据采用三次样条插值法对GDP季度数据进行了月度分解,再用X-12方法进行季节调整;常规货币政策变动rt用联邦基金利率来反映;通货膨胀率πt用居民消费价格指数(CPI)的同比变动率来衡量;参考Alfonso(2012)的研究方法,用美联储持有的国库券面值占市场流通中国库券总值的比例作为美联储非常规货币政策的代理变量mt。本文所用的全部数据均来自美联储圣路易斯分行数据库。
(二)计量方法
本文借鉴Diebold、Rudebusch和Aruoba(2006)提出的DRA模型在状态空间下研究美联储持有国债比例与美国国债利率期限结构以及宏观变量间的相互影响。DRA模型是一种在动态Nelson-Siegel模型基础上发展而来的用于研究利率期限结构与宏观经济变量之间交互作用的主流方法。它可简单表示成测量方程和转移方程两个部分。其中,测量方程从多个期限的利率时间序列中抽取出可以反映整个利率期限结构动态变化的三个潜在因子(Lt、St、Ct),如下式:
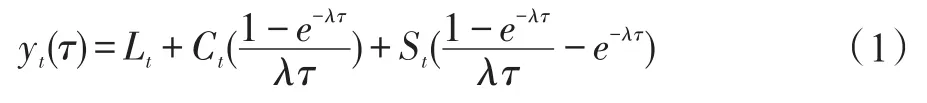
τ为到期期限;由于本文选用的数据是期限为12、24、36、60、84、120、240和360个月的利率时间序列,进而到期期限τ=12,24,…,360分别对应。Lt、St和Ct分别为水平因子、斜率因子和曲度因子。一般认为,水平因子代表利率的整体水平;斜率因子则对应着利率期限结构曲线的斜率,可以用短长期利差来表示;而曲度因子则主要与利率波动率有关。λ∈[0,1]为衰减率,λ越小,载荷衰减越慢,模型越适应期限较长的利率时间序列。为了考察利率期限结构与央行持有国债比例以及各宏观变量之间的关系,DRA模型将三个潜在因子(Lt、St和Ct)与其他变量一起组成状态因子向量xt,并假设其服从一阶向量自回归VAR(1)过程。进而,,由此转移方程可表示为④:

简记为:
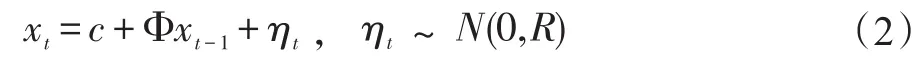
其中ηt为误差项,服从均值为0、协方差矩阵为对称矩阵R的多元正态分布⑤。综合(1)式和(2)式可得,测量方程的矩阵形式为:
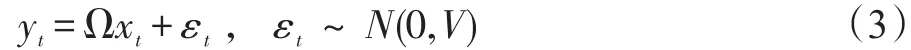
模型(3)中的系数矩阵为:
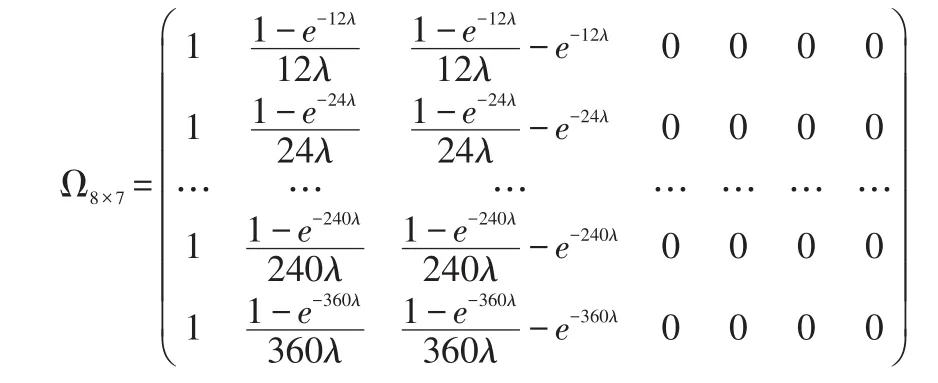
其中,Ω前三列为三个潜在因子的载荷,后面几列均为零,以保证利率期限结构动态特征完全由三个潜在因子来反映。(2)式和(3)式构成了完整的DRA模型:此模型中,央行持有国债比例与宏观经济变量、利率期限结构潜在因子在VAR框架内相互影响,其方向和程度主要通过模型(2)中的转移系数矩阵Φ得到体现。特别的,Φ最后一行的系数反映了滞后一期潜在因子和宏观变量对当期美联储持有国债比例mt的影响,而最后一列的系数则反映了滞后一期美联储持有国债比例mt-1对潜在因子和宏观变量的影响。
为了使用极大似然估计法对上述模型中的各参数c、Φ、R、λ、V进行估计,我们按照Ang和Piazzesi(2003)、吴吉林(2010)、Chadha等(2014)给出的经典处理方法,假设有三个期限的利率没有误差,而其他期限的利率存在误差,并且该误差服从正态分布,以此构建似然函数,进而得到其对数最大化条件下的参数估计值⑦。由于美国国债市场中占流通量较大份额的国债期限为1、3、10年,且多数文献证明Nelson-Siegel模型对短期和中期收益率拟合和预测效果较好,因此本文假设不存在测量误差。
三、计量结果及分析
(一)转移系数矩阵Φ的估计结果
本文侧重于研究美联储持有国债比例及其他宏观经济变量与美国国债利率期限结构潜在因子之间的交互效应。为方便观察,本文将模型(2)中VAR(1)的转移系数矩阵Φ分为左上(Φ1)、右上(Φ2)、左下(Φ3)和右下(Φ4)四个部分,如表1所示。

表1:转移系数矩阵Φ参数估计
矩阵Φ的右上角中数据所体现的是宏观经济变量对美国国债利率期限结构潜在因子的影响,可以看到,联邦基金利率rt-1和美联储持有国债的比例mt-1分别在5%和1%的显著性水平下对水平因子Lt产生正向和负向影响,其原因在于联邦基金利率作为美联储货币政策的中间目标一直扮演着基准利率的角色,联邦基金利率的上升使美国国债整体利率水平上升;当美联储在二级市场上购入长期债券时,这种大规模购债行为使市场上流通的长期债券数量减少,从而使国债价格上升、收益率下降,最终达到降低长端利率的目的。同时,联邦基金利率rt-1在5%的显著性水平下对斜率因子St产生显著影响,影响系数为-0.313,说明联邦基金利率的提高将会在短期利率提高的同时降低市场对未来通货膨胀的预期,使得长期利率下降,长短期利差收窄,收益率曲线趋于平坦。通货膨胀率πt-1对斜率因子St的影响显著为正,系数为0.070,这可能是由于当通货膨胀率上升时,市场中的经济主体预测未来通胀将延续或者进一步增大,因此长期利率上升,进而导致长短期利差扩大。曲度因子Ct在5%显著水平上受通货膨胀率πt-1的负向影响、美联储持有国债比例mt-1的正向影响,系数分别为-0.155和0.088。这可能是美国作为2008年全球金融危机的发源地,经济面临下行风险,通缩压力不断增大,导致金融市场内的不确定性增加,从而引起国债利率的波动性增加;而美联储在二级市场买入大量国债作为央行的一种市场干预手段,购债同时使得大量资金涌入债券市场,不仅加剧了债市波动,而且投资者担心政府的过度干预会干扰债券及其他金融产品的定价,造成市场的进一步扭曲,增加市场中蕴含的风险。
矩阵Φ的左下角中数据所体现的则是美国国债利率期限结构潜在因子对宏观经济变量及央行持有国债比例的影响。可以看到,三个潜在因子都对经济增长率gt产生显著的负向影响。这是因为国债利率作为一国的基准利率,整体水平的上升会提高本国的资金使用成本,从而大幅降低民间投资积极性;而长短期利差的增大则反映了民众预期未来的通胀率将上升,经济中的不确定性增加;曲度因子反映了国债利率的波动性,当曲度因子增大时,表明国债市场的波动性增加,金融市场中蕴含的不确定性和风险性增大,这三方面都会在一定程度上抑制经济的快速增长。曲度因子Ct和联邦基金利率rt-1存在同向变动特征,说明当经济中的不确定性和风险性增加时,美国国债利率的波动性提高,此时美联储将通过提高联邦基金利率对市场进行干预,以稳定市场预期。最后可以看到水平因子Lt-1、斜率因子St-1都在1%的显著水平下对美联储持有国债比例产生正向影响,系数分别为0.500和0.330。由于水平因子Lt、斜率因子St分别表示国债的长期利率水平和短长期利差,这二者中无论哪种因素的提高都会迫使美联储扩大中长期国债的购买量以稳定中长期利率水平,为市场营造宽松稳定的投资环境。
矩阵Φ的右下角中数据则解释了各宏观变量间的相互影响。对角线上的系数都在1%的水平上显著,说明各宏观变量的变动都存在较强持续性。通过观察可知,通货膨胀水平πt-1、联邦基金利率rt-1都会对美联储持有国债比例mt在1%的显著水平上产生显著的负向影响。经济的下行往往伴随着通货紧缩,此时央行为避免经济陷入衰退,会降低基准利率以刺激民间投资,但是由于银行惜贷等一系列原因,短期利率的变动并不能有效引起长期利率的下降,投资环境没有得到根本改善,而央行此时大规模购买中长期国债将向市场直接注入流动性,为市场提供宽松环境的同时降低了长期利率,并进一步传达出政府货币宽松的政策信号,使市场参与者形成稳定预期。同时,通货膨胀率πt-1、联邦基金利率rt-1和经济增长率gt呈现出正相关关系,可以解释为当经济形势向好时往往伴随着温和的通货膨胀,此时美联储的利率政策也从刺激经济时的超低利率转向正常利率水平,以防经济增长速度过快而引发恶性通货膨胀。
(二)脉冲响应分析
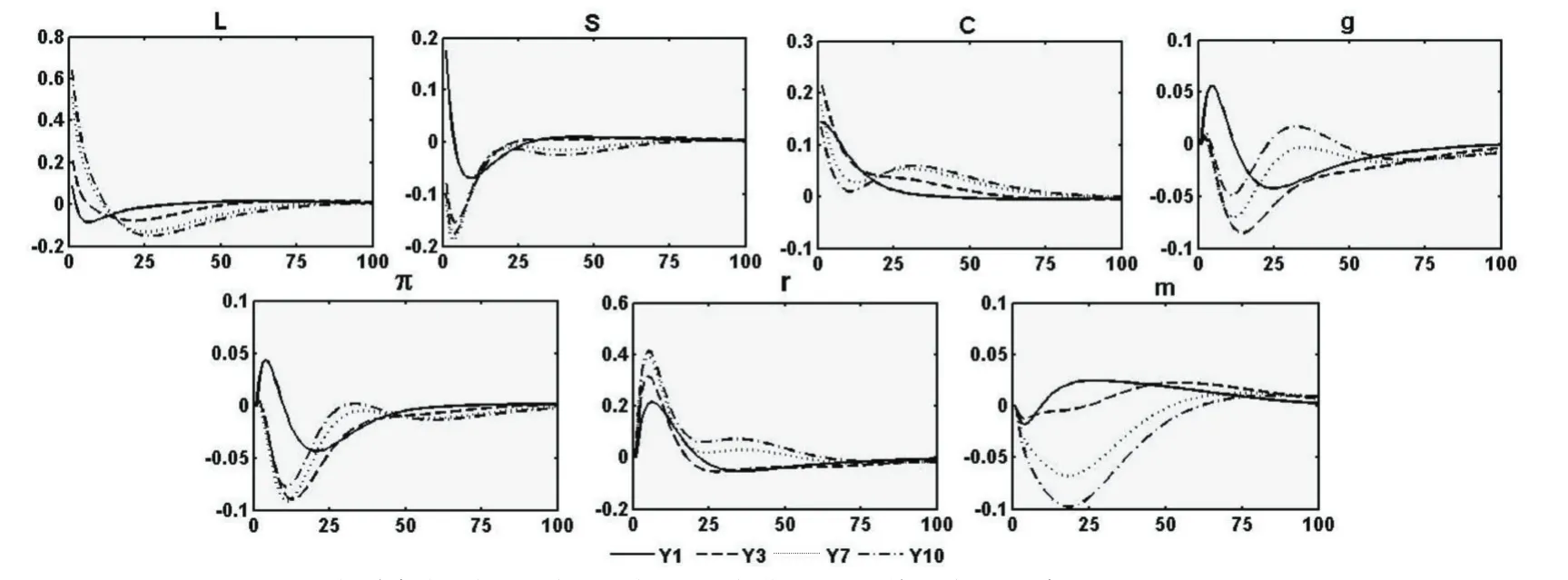
图3:潜在因子、宏观变量脉冲—利率期限结构响应图
为避免某一因素变动引起同期其他因素扰动而引起估计结果出现误差,本文采用乔利斯基(cholesky)分解对脉冲响应进行分析。引入脉冲响应的变量顺序为水平因子Lt、斜率因子St、曲度因子Ct、经济增长率gt、通货膨胀率πt、联邦基金利率rt和美联储持有国债比例mt。考察分别在潜在因子、宏观变量和美联储持有国债比例变量的随机误差项上施加一个标准差的冲击后,对1年期(Y1)、3年期(Y3)、7年期(Y7)和10年期(Y10)这四个关键期限利率产生的影响,结果见图3。
由图3可以看到,对于各潜在因子施加1个标准差的冲击,各期限美国国债收益率都能够迅速做出反应。在水平因子的冲击下,各期限收益率都呈现出逐渐衰减到0的特征,但是到期期限越长,当期反应越大,衰减速度越慢;在斜率因子的冲击下,各期限国债收益率均迅速下降后趋于平稳,但是到期期限短的利率在当期出现了正向反应,衰减后出现了轻微的反弹;而到期期限长的利率期初出现负向反应后经历了较大程度的上升最后趋于平稳。受曲度因子冲击后各期限收益率的响应与水平因子下的响应模式类似,但到期期限不同的国债收益率曲线之间并没有出现明显的分化。
进一步观察各宏观变量的脉冲响应图,我们发现各期限债券收益率对宏观变量冲击的响应均存在一定的滞后性。各期限收益率在经济增长率1个单位标准差的冲击下,呈现出波浪形变动的特征;短期国债的收益率受经济增长率冲击的影响较大。在通货膨胀因素的冲击下,各期限收益率的变化路径基本相同,都经历了先下降再上升后趋于稳定的过程,但短期国债收益率的波动幅度较大。在联邦基金利率的冲击下,各期限美国国债收益率迅速上升后趋于下降,而且到期期限越长,收益率响应幅度越大。在美联储持有国债比例增加的冲击下,不同期限国债收益率的变动出现了明显的分化。在短期国债收益率小幅上升的同时,长期国债收益率明显下降。这可能是由于在债券市场存在市场分割的情况下,伴随着“扭曲操作”的美联储大规模购债计划,使得部分资金从短期市场流入长期国债市场,进而在压低长期国债利率的同时,小幅推升了短期国债收益率,而且美联储购买中长期高质量债券向市场传达出向这些债券提供隐性支持和维持货币宽松的政策意图,也有助于长期国债收益率的进一步下降。
四、总结及政策意义
本文采用DRA模型对美联储持有国债比例变化与美国国债利率期限结构以及宏观经济变量之间的交互效应进行了研究。实证结果显示:(1)美联储持有国债比例变化对国债利率期限结构的水平因子和曲度因子存在显著影响,央行持有国债比例的提高有助于降低国债利率的整体水平,但会加大债券市场的价格波动幅度。(2)通过对脉冲响应结果的分析发现,在美联储持有国债比例提高的冲击下,长期国债利率的响应为负,且到期期限越长的国债收益率受美联储持有国债比例提高冲击的反应越强烈,下降幅度越大。
上述研究一方面有助于加深我们对近年来发达国家非常规货币政策作用途径和效果的认识;另一方面,对于分析美联储实施缩减资产负债表政策可能造成的影响具有借鉴意义。从长期看,美联储的“缩表”政策将降低其持有国债的比例,这会对中长期利率有推升作用,这使得我们在关注和预测美国货币政策的未来实施进程时,要注意考虑美联储“缩表”和加息政策的协调和配合问题。
注:
①数据来源于美联储圣路易斯分行官网https://fred.stlouisfed.org。
②6%的美联储相对资产规模(FRE/GDP)由美国1920—1930年以及1950—2007年平均水平求得。
③数据来源自美国劳工部官网https://www.bls.gov/。
④本文选择滞后一阶VAR模型,是因为作为DRA模型中的转移方程,VAR模型不能直接含有二阶(含)以上的滞后变量,必须重新定义状态向量。而且滞后阶数较多时,待估计参数过多,影响估计量的有效性。
⑤文章假定R为对称矩阵,即允许各潜在变量和宏观变量间的冲击可以相互影响。例如央行货币政策的变动,不仅会使银行间同业拆借利率,也会导致经济增长率和通货膨胀率的变化,且似然比检验结果显示该设定形式合理。
⑥V取为对角矩阵,正如很多无套利模型都设定收益率模型的误差项是独立同分布的,即不同到期期限收益率的误差项不相互影响。
⑦之所以这样设定是因为似然函数的构建主要基于可观测变量的概率分布,在DRA模型中却同时存在可观测变量和不可观测变量,为此需要把不可观测的潜在因子转化为可观测的利率,于是假定三个期限对应的收益率曲线没有测量误差。
[1]Hamilton J D,Jing Cynthia Wu.2012.The Effectiveness of Alternative Monetary Policy Tools in a Zero Lower Bound Environment[J].Journal of Money,Credit and Banking,44(Supplement).
[2]Chadha J S,Waters A.2014.Applying a macro-finance yield curve to UK quantitative Easing[J].Journal of Banking&Finance,39(1).
[3]Kaminska I,Zinna G.2014.Official Demand for U.S.Debt:Implications for U.S.Real Rates[J].Ssrn Electronic Journal,14(66).
[4]Eser F,Schwaab B.2016.Evaluating the impact of unconventional monetary policy measures:Empirical evidence from the ECB’s Securities Markets Programme[J].Journal of Financial Economics,119(1).
[5]Diebold F X,Rudebusch G D,Aruoba S B.2006.The Macroeconomy and the Yield Curve:A Dynamic Latent Factor Approach[J].Journal of Econometrics,2006b,131(s1-2).
[6]Alfonso Palacio Vera.2012.Debt monetization,inflation,and the“neutral”interest rate,International Review of Applied Economics,Vol.26,No.2,March.
[7]Ang A,Piazzesi M.2003.A no-arbitrage vector autoregression of term structure dynamics with macroeconomic and latent variables[J].Journal of Monetary Economics,50(4).
[8]邓晓兰,李铮,黄显林.公共债务货币化对利率的影响研究:理论与美国经验[J].经济问题探索,2014,(11).
[9]吴吉林,金一清,张二华.潜在变量、宏观变量与动态利率期限结构——基于DRA模型的实证分析[J].经济评论,2010,(1).

