星载激光光斑影像质心自动提取方法

袁小棋,李国元,唐新明,高小明,黄庚华，李 野

1. 长春理工大学，吉林 长春 130022； 2. 国家测绘地理信息局卫星测绘应用中心,北京 100048; 3. 江苏省地理信息资源开发与利用协同创新中心，江苏 南京 210023; 4. 中科院上海技术物理研究所，上海 200083； 5. 中国科学院空间主动光电技术重点实验室，上海 200083

星载激光测高技术在获取高程控制点[1]、极地冰盖测量[2-3]、森林生物量的测量[2]等诸多方面有着其独特的优势。随着我国激光测高技术的发展，资源三号02星上首次搭载了试验性对地观测的激光测高仪，并成功获取有效测高数据，虽然相比美国的GLAS还有一定差距，但已经实现零的突破[4-5]，相比较而言，除缺少波形记录功能，同时也缺少对激光发射时能量状态记录的装置。但在后续的高分七号卫星、陆地生态系统碳监测卫星上搭载的激光测高载荷均配备足印相机，能对激光光斑的能量分布进行有效成像，辅助确定激光的指向[6]。在美国的ICESat(ice cloud land elevation satellite)卫星上搭载的地球科学激光测高系统GLAS(geoscience laser altimeter system)带有能够记录激光发射时光斑能量分布的相机LPA(laser profile array)，获取更加准确的激光指向信息以及激光状态信息[7]。其中LPA与国产星载激光测高仪中的足印相机有着相似的功能，因此研究LPA的几何参数信息提取对于国产卫星激光测高数据处理有一定的价值与意义。

针对激光光斑质心的提取方法比较多样化。在较早时期有基于Hough变换[8]、基于Hessian矩阵[9]等求图像中心的方法。灰度重心法是早期较为常用的方法，其方法简单，但是该方法在光斑形状不规则、强度不对称时存在很大的局限性[10]。曲线拟合也是比较常用的方法之一，但是边缘和阈值的选取都会对质心提取的精度产生很大影响[11]。文献[12]提出一种随机抽取6个样本点后拟合椭圆，将样本点中到达该椭圆距离超过阈值的点剔除后，将所有样本点椭圆拟合求出质心，该方法大大提高了精度。文献[13]提出了利用N幅图像前后差分去噪声后利用圆拟合求得质心的方法；文献[14]提出一种针对光斑内部存在缺失的误差函数拟合的算法。高斯拟合法是近些年较为常用的质心提取方法，精度高，但是计算较为复杂。改进的方法有很多，文献[15]提出利用光斑中的不饱和点进行高斯曲面拟合求质心的方法；文献[16]提出了高斯曲面解析法和定参高斯拟合法。还有诸多以高斯拟合法为基础的改进方法[17-18]。文献[19]提出利用一阶导数零交叉点的方法确定峰值像素坐标后利用高斯拟合求出准确质心，进而提高运算效率。文献[20]提出通过将光斑映射到物方空间坐标系后圆拟合法求取质心的方法。但是以上方法要么在图像的预处理中对噪声的滤除不彻底，要么不是用于激光光斑的质心提取。本文提出用高斯拟合的峰值分割图像，进而去除噪声对光斑质心提取影响的方法。

1 常用研究方法

1.1 灰度重心法

灰度重心法主要是以灰度作为权重计算出图像的质心，公式如下

(1)

(2)

式中，(x0,y0)是光斑的质心；I(i,j)是图像上第i行第j列的灰度值。该方法简单快速，但是在图像复杂，形状不规则的时候提取精度通常不高。

1.2 高斯拟合法

在理想情况下，光斑的强度分布应该符合高斯分布，所以高斯曲面拟合法有着精确度高，在图像复杂且形状多变的情况下同样适用等诸多优点，公式如下

(3)

式中，A是光斑的幅值；(x0,y0)是该光斑的质心；δx、δy分别是x、y方向上的标准差；I(x,y)是像元坐标为(x,y)时的强度值。

将式(3)化简为

(4)

将其对应成多项式

z=ax2+by2+cx+dy+f

(5)

通过最小二乘法可以计算出多项式对应的系数

(6)

式中，质心点坐标与幅值可求，如下

(7)

该方法虽然总体精度较高，但是由于CCD存在一定的背景噪声，并且计算程度复杂，在背景噪声去除后，会造成一定的不确定的偏差。

1.3 椭圆拟合法

椭圆拟合法是根据边缘检测结果，通过最小二乘法对边缘进行椭圆拟合，求出椭圆的中心代替图像中光斑的质心。一般椭圆公式如下

ax2+bxy+cy2+dx+ey+f=0

(8)

利用差值最小的原理求出参数a、b、c、d、e、f的最优解，得到椭圆的一般方程，通过最优解，计算出质心点坐标。质心的表达式如下

(9)

(10)

该方法较为简单、高效，但在光斑强度不对称或者边缘模糊的情况下，会造成较为严重的计算误差。

2 基于阈值分割的椭圆拟合法

本方法结合高斯拟合法与椭圆拟合法两种方法。理想情况下激光光斑应呈现标准的高斯分布，所以通过高斯拟合可以确定光斑的质心。由于存在一定的随机噪声和背景辐射噪声，在高斯拟合过程中，高斯峰值会存在一定的下降，将高斯峰值作为阈值可将质心位置缩小到一个非常小的范围内，在最大程度上减少噪声对光斑质心提取的影响，同时尽量消除椭圆拟合法不涉及灰度值的问题，然后在通过高斯峰值确定的范围内通过最小二乘法进行椭圆拟合，求出椭圆的质心，即为光斑的质心。

具体方法如下：通过高斯拟合法求出高斯峰值，然后以高斯峰值为阈值，对图像进行阈值分割，分割后通过LOG边缘检测[21]确定质心范围边界，利用椭圆拟合法求得质心，将这个求得的质心作为光斑质心。计算流程如图1所示。

图1 基于阈值的椭圆拟合法流程图Fig.1 Flow chart of ellipse fitting method based on threshold

3 试验结果

3.1 试验数据

仿真数据是通过分析CCD噪声的来源、背景噪声仿真已知质心的高斯光斑[22-23]。分别仿真20×20的光斑矩阵和120×120光斑矩阵。其中20×20光斑矩阵的尺度与LPA尺度相同，为LPA的质心提取提供试验依据。120×120光斑矩阵的质心提取，证明该方法的普适性。试验数据仿真的是标准高斯椭圆光斑，然后将其灰度值拉伸到255，再加入一定的背景噪声和因为CCD成像方式导致的随机噪声。但该仿真数据暂未考虑卫星抖动引入的噪声。

本文研究针对的主要数据是来自搭载在GLAS上的LPA记录的数据。LPA是一个80×80的像素阵列，其作用主要是记录激光出射时的光斑能量分布，检测出射光斑的有效性，在GLAS04级产品上给出LPA记录的20×20的矩阵，用数字0～255表示记录的激光能量值。光斑的形状会随着激光器能量的衰减、平台的抖动、入射角度发生变化，造成光斑不是标准的高斯圆形分布。GLAS共搭载了3个激光器[24]，由于工作时间不同，输出的激光光斑也有一定的差别，所以本文分别选取了不同时期的光斑作为研究数据。由于GLAS上搭载的L1激光器工作初期状态不好而停用，所以本文选择卫星状态更为稳定的L2首次工作的初期阶段[24]，2003年10月15日、2004年2月20日和2004年5月22日，共3天，取其中3 h的光斑进行质心提取并对质心点进行了统计与分析。因为在激光器工作初期，激光能量较大，且工作状态良好，故认为记录的光斑具有可应用性。

3.2 仿真数据质心提取

对仿真数据20×20和120×120两种尺寸的高斯光斑分别用常用的3种方法和本文介绍的方法进行质心点的提取，然后统计这4种方法提取的质心与仿真光斑真实质心的距离。

20×20的仿真图像光斑质心为(10,10)，120×120的仿真图像光斑质心为(50,50)，图像如图2所示，对光斑提取的质心统计如表1。

图2 仿真光斑图像Fig.2 Emulation spot image

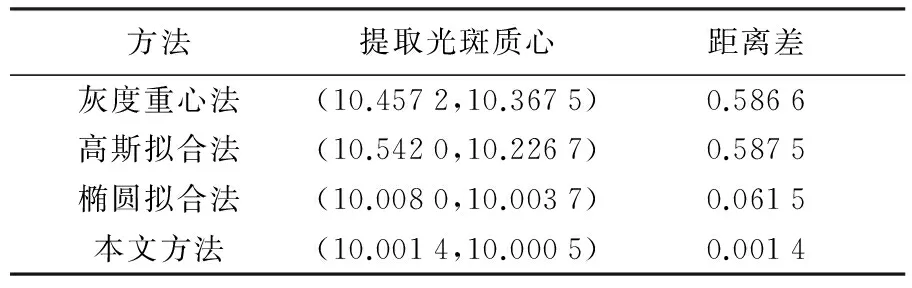
方法提取光斑质心距离差灰度重心法(10.4572,10.3675)0.5866高斯拟合法(10.5420,10.2267)0.5875椭圆拟合法(10.0080,10.0037)0.0615本文方法(10.0014,10.0005)0.0014

表2120×120的不同方法质心点统计

Tab.2120×120differentmethodsofcentroidpointstatistics

方法提取光斑质心距离差灰度重心法(58.6792,58.3223)12.0245高斯拟合法(56.7881,54.5324)8.1622椭圆拟合法(50.3702,50.5555)0.6676本文方法(50.0854,49.9977)0.0854

通过表1和表2的比较可以看出通过高斯拟合确定阈值后椭圆拟合方法求得的质心更加接近仿真的质心，而灰度重心法得到的结果较差。在这两组数据中椭圆拟合的效果均好于高斯拟合，但是不能得出椭圆拟合好于高斯拟合的结论，因为仿真图像形状规则且对称，对于光斑质心出现偏移等情况时，未考虑灰度值的椭圆拟合法会出现较大偏差。仿真数据中影响光斑边缘的噪声比较小，所以椭圆拟合的优势比较明显，在形状不规则或者光斑强度分布不是很理想的情况下，并不能确定上述两种方法的优劣，还需进一步的证明。但可以说明在边缘清晰、形状规则的光斑下椭圆拟合具有一定的优势。

3.3 LPA数据质心提取

首先采用3种常用方法和本文方法对2003年10月15日的一幅LPA进行质心提取，结果见表3、图3。然后分别选取2003年10月15日、2004年02月20日和2004年05月22日中一个GLAH04文件进行多幅LPA影像的激光光斑质心提取，并对质心点的变化规律进行统计分析。在NASA的网站上下载得到GLAS04的格式为H5的产品，通过HDFView提取出记录LPA数据i_PixInt的文件，LPA记录的数据频率为40 Hz，与激光的发射频率相同。

表3 LPA质心位置

如图4是对2003年10月15日其中10 s进行的统计，发现最大振幅为0.07个像素/次，平均振幅为0.009 8个像素/次，因为LPA的视场角为0.08°，LPA由80×80个像素组成，卫星运行在600 km的高空，通过对地面的投影，计算得到LPA的空间分辨率约为10.4 m(文献[25])。所以，0.009 8个像素的变化可忽略不计。

图5是对3 h的LPA所有光斑质心位置的分析。统计质心位置的最大变化量，3个时间段的结果如表4所示。

从图5中的质心坐标位置可以看出，质心的行列坐标都呈周期性的变化，卫星轨道周期大约1.5 h，这与轨道运行周期90 min刚好相符合，也证明了质心变化的规律性。而且从图5中可以看出，质心在行变化的幅度较小，而列变化的幅度较大。

表4 LPA试验数据质心变化统计表

在对2004年05月22日数据统计过程中，存在一定的异常值，但仍然可以看出存在着1.5 h为一个周期的变化规律，在不计异常值的情况下，质心的最大变化仍然有2.7个像素，在一个像素代表10 m的情况下，激光质心在地面的位置变化约27 m，对应指向角误差约9″。随着时间的变化，质心的抖动越来越剧烈，所以不能以初期试验室的质心指向代表所有时期的质心指向。通过LPA说明采用在轨监视记录激光光斑影像对于精确测量激光指向非常重要。精确的激光指向测量对平面以及高程精度的提高都有重要的意义。

图3 2003年10月15日的LPA图像Fig.3 The LPA in partial October 15，2003

图4 2003-10-15某10 s坐标统计Fig.4 The change of LPA centroid in partial October 15，2003

图5 2003-10-15某3 h坐标统计Fig.5 The change of LPA centroid column in partial October 15，2003

4 结 论

质心提取的常用方法普遍存在抗噪声干扰能力不强的问题，本文利用高斯曲面拟合获得峰值，再将峰值设为阈值，对图像进行阈值分割后，利用椭圆拟合的方法求取光斑的质心。该方法通过缩小椭圆拟合的计算范围，去除噪声的干扰，解决了背景噪声对光斑质心提取存在影响的问题。通过仿真光斑的试验，以及利用本文方法对GLAS上的LPA数据进行质心的提取，并统计质心随时间变化的规律，能得出如下结论：

(1) 根据激光在CCD上成像特性仿真的光斑图像质心提取试验中，本文方法得到较灰度重心法、高斯拟合法、椭圆拟合法更为精确的试验结果，且在两种尺度上均有良好的提取结果，进一步证明了本文方法的适用性。

(2) 利用本文方法对GLAS中的LPA数据进行质心提取，LPA质心变化周期为1.5 h，与卫星轨道运行周期90 min相同，说明卫星激光指向随轨道位置变化产生较大偏差。在短时间内光斑质心位置存在一定的高频抖动，GLAS激光器在短时间内抖动范围很小，但长期存在较大变化且有一定的规律性，通过在轨监视激光光斑质心变化能有效提高激光指向角测量精度，进而提高激光定位精度。

未来的高分七号、陆地生态系统碳监测卫星上搭载的激光测高仪均配备有足印相机，能记录激光光斑的空间能量分布情况，高精度的光斑质心提取将是确保激光指向精度的一个重要步骤。结合国产卫星激光测高仪足印相机的特点，研究高精度的光斑质心提取算法将是下一步的重点。

[1] 李国元, 唐新明, 张重阳, 等. 多准则约束的ICESat/GLAS高程控制点筛选[J]. 遥感学报, 2017, 21(1): 96-104.

LI Guoyuan, TANG Xinming, ZHANG Chongyang, et al. Multi-criteria Constraint Algorithm for Selecting ICESat/GLAS Data as Elevation Control Points[J]. Journal of Remote Sensing, 2017, 21(1): 96-104.

[2] HUANG Huabing, CHENG Xiao, GONG Peng, et al. A New 1000 m Digital Elevation Model for Antarctica by Integrating ICESat/GLAS and Envisat RA-2 Data[J]. Journal of Remote Sensing, 2014, 18(1): 117-125.

[3] 陈国栋, 李建成, 褚永海, 等. 利用ICESat数据确定北冰洋海冰出水高度——以2005—2006年为例[J]. 测绘学报, 2015, 44(6): 625-633. DOI: 10.11947/j.AGCS.2015.20140478.

CHEN Guodong, LI Jiancheng, CHU Yonghai, et al. Determination of Sea Ice Freeboard in Arctic from ICESat: Case Study of 2005-2006[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(6): 625-633. DOI: 10.11947/j.AGCS.2015.20140478.

[4] 段祝庚, 肖化顺. 基于GLAS数据的森林生物量估算研究进展[J]. 林业资源管理, 2013(1): 86-90, 94.

DUAN Zhugeng, XIAO Huashun. Review of the Methods for Forest Biomass Estimation with GLAS Data[J]. Forest Resources Management, 2013(1): 86-90, 94.

[5] 唐新明, 李国元, 高小明, 等. 卫星激光测高严密几何模型构建及精度初步验证[J]. 测绘学报, 2016, 45(10): 1182-1191. DOI: 10.11947/j.AGCS.2016.20150357.

TANG Xinming, LI Guoyuan, GAO Xiaoming, et al. The Rigorous Geometric Model of Satellite Laser Altimeter and Preliminarily Accuracy Validation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(10): 1182-1191. DOI: 10.11947/j.AGCS.2016.20150357.

[6] 李国元. 对地观测卫星激光测高数据处理与工程实践[D]. 武汉: 武汉大学, 2017.

LI Guoyuan. Research on the Several Key Techniques of Earth Observation Satellite Laser Altimeter Data Processing and Application[D]. Wuhan: Wuhan University, 2017.

[7] BAE S, WEBB C, SCHUTZ B. GLAS PAD Calibration Using Laser Reference Sensor Data[C]∥AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Providence, Rhode Island: AIAA, 2004.

[8] 杨耀权, 施仁, 于希宁, 等. 用Hough变换提高激光光斑中心定位精度的算法[J]. 光学学报, 1999, 19(12): 1655-1660.

YANG Yaoquan, SHI Ren, YU Xining, et al. An Algorithm to Raise the Locating Precision of Laser Spot Center Based on Hough Transform[J]. Acta Optica Sinica, 1999, 19(12): 1655-1660.

[9] STEGER C. An Unbiased Detector of Curvilinear Structures[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(2): 113-125.

[10] 尚学军, 何明一, 王军良. 基于线阵CCD的光斑定位算法研究[J]. 激光与红外, 2008, 38(7): 730-731, 740.

SHANG Xuejun, HE Mingyi, WANG Junliang. Research of Method in Light-spot Location Based on Linear CCD[J]. Laser & Infrared, 2008, 38(7): 730-731, 740.

[11] 王敏, 赵金宇, 陈涛. 基于各向异性高斯曲面拟合的星点质心提取算法[J]. 光学学报, 2017, 37(5): 0515006.

WANG Min, ZHAO Jinyu, CHEN Tao. Center Extraction Method for Star-map Targets Based on Anisotropic Gaussian Surface Fitting[J]. Acta Optica Sinica, 2017, 37(5): 0515006.

[12] 闫蓓, 王斌, 李媛. 基于最小二乘法的椭圆拟合改进算法[J]. 北京航空航天大学学报, 2008, 34(3): 295-298.

YAN Bei, WANG Bin, LI Yuan. Optimal Ellipse Fitting Method Based on Least-square Principle[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(3): 295-298.

[13] 张奔牛, 万红明, 毛成林. 基于差分光斑中心定位算法的位移传感技术研究[J]. 传感技术学报, 2011, 24(2): 215-219.

ZHANG Benniu, WANG Hongming, MAO Chenglin. Study on Displacement Sensor Based on Difference Operation Spot Center Location Algorithm[J]. Chinese Journal of Sensors and Actuators, 2011, 24(2): 215-219.

[14] QUINE B M, TARASYUK V, MEBRAHTU H, et al. Determining Star-image Location: A New Sub-pixel Interpolation Technique to Process Image Centroids[J]. Computer Physics Communications, 2007, 177(9): 700-706.

[15] 王丽丽, 胡中文, 季杭馨. 基于高斯拟合的激光光斑中心定位算法[J]. 应用光学, 2012, 33(5): 985-990.

WANG Lili, HU Zhongwen, JI Hangxin. Laser Spot Center Location Algorithm Based on Gaussian Fitting[J]. Journal of Applied Optics, 2012, 33(5): 985-990.

[16] 冯新星, 张丽艳, 叶南, 等. 二维高斯分布光斑中心快速提取算法研究[J]. 光学学报, 2012, 32(5): 0512002.

FENG Xinxing, ZHANG Liyan, YE Nan, et al. Fast Algorithms on Center Location of Two Dimensional Gaussian Distribution Spot[J]. Acta Optica Sinica, 2012, 32(5): 0512002.

[17] 王海涌, 费峥红, 王新龙. 基于高斯分布的星像点精确模拟及质心计算[J]. 光学 精密工程, 2009, 17(7): 1672-1677.

WANG Haiyong, FEI Zhenghong, WANG Xinlong. Precise Simulation of Star Spots and Centroid Calculation Based on Gaussian Distribution[J]. Optics and Precision Engineering, 2009, 17(7): 1672-1677.

[18] 贾瑞明, 马晓蕾, 郝云彩. 基于偏正态分布的星点细分定位方法研究[J]. 激光与光电子学进展, 2016, 53(5): 051002.

JIA Ruiming, MA Xiaolei, HAO Yuncai. Research on Star Subdivision Location Method Based on Skewed Normal Distribution[J]. Laser & Optoelectronics Progress, 2016, 53(5): 051002.

[19] 赵婧鑫, 周富强. 小尺寸光斑中心的高精度定位算法[J]. 红外与激光工程, 2014, 43(8): 2690-2693.

ZHAO Jingxin, ZHOU Fuqiang. High-precision Center Location Algorithm of Small-scale Focal Spot[J]. Infrared and Laser Engineering, 2014, 43(8): 2690-2693.

[20] 詹银虎, 郑勇, 张超, 等. 超大视场太阳敏感器图像质心提取算法[J]. 测绘学报, 2015, 44(10): 1078-1084. DOI: 10.11947/j.AGCS.2015.20150118.

ZHAN Yinhu, ZHENG Yong, ZHANG Chao, et al. Image Centroid Algorithms for Sun Sensors with Super Wide Field of View[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1078-1084. DOI: 10.11947/j.AGCS.2015.20150118.

[21] 贺强, 晏立. 基于LOG和Canny算子的边缘检测算法[J]. 计算机工程, 2011, 37(3): 210-212.

HE Qiang, YAN Li. Algorithm of Edge Detection Based on LOG and Canny Operator[J]. Computer Engineering, 2011, 37(3): 210-212.

[22] 刘兆蓉, 王志乾, 刘绍锦, 等. 激光光斑中心精确定位算法研究[J]. 计算机仿真, 2011, 28(5): 399-401, 409.

LIU Zhaorong, WANG Zhiqian, LIU Shaojin, et al. Research of Precise Laser Spot Center Location Algorithm[J]. Computer Simulation, 2011, 28(5): 399-401, 409.

[23] 张爱丽, 佟首峰, 韩成, 等. 基于CCD的光斑能量分布测量及特性分析[J]. 激光与红外, 2011, 41(6): 622-626.

ZHANG Aili, TONG Shoufeng, HAN Cheng, et al. Facula Energy Measurement and Analysis Based on CCD[J]. Laser & Infrared, 2011, 41(6): 622-626.

[24] ABSHIRE J B, SUN Xiaoli, RIRIS H, et al. Geoscience Laser Altimeter System (GLAS) on the ICESat Mission: On-orbit Measurement Performance[J]. Geophysical Research Letters, 2005, 32(21): L21S02.

[25] YADAV G K. Simulation of ICESat/GLAS Full-Waveform over Highly Rugged Terrain[D]. Amsterdam: University of Twente, 2010.