简谐运动位移方程和平均值公式的应用

郑 金

(凌源市职教中心,辽宁 朝阳 122500)

对于简谐运动,偏离平衡位置的位移即振动位移的起点始终在平衡位置,其大小为振动物体偏离平衡位置的距离,方向从平衡位置指向物体所在的位置.振动位移随时间按正弦规律变化,若从平衡位置开始计时,则振动位移方程为x=Asinωt;若从振动端点开始计时,则振动位移方程为x=Acosωt.在解题时,需根据题意来选择合适的位移方程.

1 简谐运动位移方程的应用

对于某些简谐运动问题,需利用振动位移方程来解答,但振动位移方程有两种不同的形式,关键是根据题意选择计时起点是在平衡位置还是在振动端点,由此写出相应的位移方程.

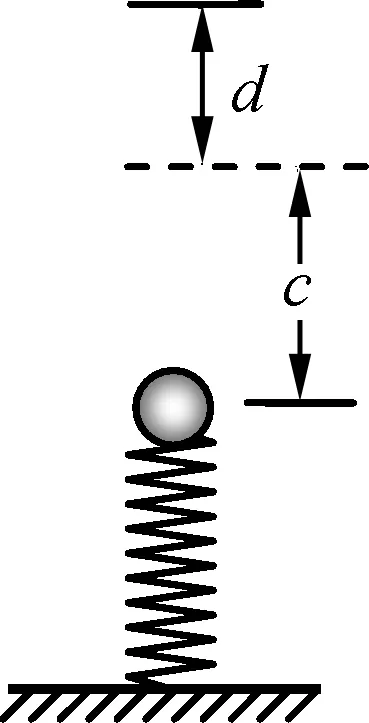
图1

例1.如图1所示,一劲度系数为k的竖直轻质弹簧的下端固定在水平面上,开始时弹簧处于原长状态,现将一小球放在弹簧上端,弹簧被压缩d后平衡,然后按住小球使弹簧再压缩c,且c>d,从放开小球开始计时,求小球在运动过程中与弹簧接触的时间.

解析:由于c>d,利用简谐运动的对称性可知,小球在向上运动过程中一定会离开弹簧继续上升,因此小球在离开弹簧之前做简谐运动,离开弹簧后做竖直上抛运动.

图2

例2.如图2所示,小车质量为M,由静止开始沿着倾斜角为α的光滑斜面从高度为h处滑下,与一个轻弹簧缓冲器相碰而自由振动,然后又冲上斜面.若缓冲弹簧的劲度系数为k,求: (1) 在缓冲器上弹簧的最大压缩量是多少?(2) 小车和弹簧在第一次接触过程中被缓冲的时间为多少?

解析: (1) 设最大压缩量为xm,由机械能守恒定律有

解方程可得

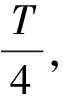
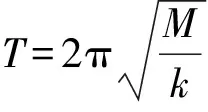
设小车开始压缩弹簧到达平衡位置时发生的位移为x0,即弹簧压缩量为x0,则有受力平衡方程

Mgsinα=kx0,

可知简谐运动的振幅为

若从小车经平衡位置开始计时,则振动位移方程为x=Asinωt,可知振动位移从0增大到x0的过程经历的时间为

所以小车被弹簧缓冲的时间为

对压缩弹簧的全过程应用机械能守恒定律列方程求最大压缩量非常简单.在求缓冲时间时,需对两个运动过程分别求出时间,但要注意小车被缓冲的过程不只是小车压缩弹簧的过程,而是小车与弹簧相互作用的整个过程.

2 正弦平均值公式的应用

例3.有一个竖直弹簧振子,轻弹簧的劲度系数为k,小球的质量为m,若在弹簧处于自然状态时突然释放小球,对于小球从速度为0变到最大的过程,求: (1) 弹簧弹力的冲量; (2) 小球受到合力的冲量.

方向竖直向上.

还有一种方法,合力的大小为

F=mg-f=mgcosωt,

对于弹簧弹力的冲量,关键是推导出弹簧形变量的表达式,而且利用正弦平均值来求弹力的平均值,可避免积分运算过程.要注意物体在简谐运动过程中偏离平衡位置的位移、对初始位置的位移和弹簧形变量3者之间的关系.对于合力的冲量,也可利用最大速度公式vm=Aω和动量定理来求解.

图3

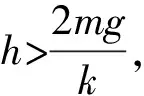
解析: (1) 小球在竖直方向做加速度减小的加速运动,当合力为0时速度达到最大,此时ky1=mg,可知作用力F=ky的平均值为

对小球的运动过程由动能定理有

可得最大速度为

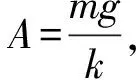
小球在竖直方向的运动相当于竖直弹簧振子从弹簧形变量为0时开始向下运动,即从振动端点向平衡位置运动，可知某时刻的振动位移大小为x=Acosωt,则小球向下运动发生的位移大小为y=A-Acosωt,相当于弹簧的形变量，因此小球受到平板的作用力的大小为F=ky=mg(1-cosωt),方向向上,那么平板受到小球的作用力方向向下,可知平板受到水平地面的摩擦力大小为

f=μ(Mg+F)=μ(M+m)g-μmgcosωt.

摩擦力的平均值为

对平板的减速运动过程由动量定理有

可得小球第一次达到最大速度时平板的速度为

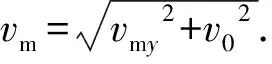
对于例题1和例题2的解答,利用了位移方程x=Asinωt;对于例题3和例题4的解答,利用了位移方程x=Acosωt，其方向跟运动方向相反.

总之,对有关简谐运动竞赛题的解答,需灵活应用位移方程和正弦平均值公式.简谐运动的位移方程有两种不同的形式,在选用方程时,关键是看振动物体的出发点是在平衡位置还是在振动端点,如果出发点不在这两个特殊位置,则需利用运动的可逆性把运动的出发点选在平衡位置或振动端点,由此写出振动位移方程.要注意物体振动位移与实际运动发生的位移有时不相等.直接利用正弦平均值与最大值的关系解题,可避免微积分的运算过程,从而化繁为简.