聚焦核心素养,追寻真实逻辑
——以“动量守恒定律”教学为例
唐建勋
(无锡市辅仁高级中学,江苏 无锡 214123)
最新版的《普通高中物理课程标准》已经出台,课程的基本理念就在于体现物理学科本质,培养现代公民必备的核心素养.其中物理学科的核心素养由“物理观念”、“科学思维”、“科学探究”、“科学态度与责任”4个方面构成,这些核心素养的内涵对我们的课堂教学设计都提出了更明确的要求.现以“动量守恒定律”一课的教学为例探讨如何在课堂教学中聚焦核心素养,促进学生发展.
1 教材安排的解读
历史发展的时间线和物理学知识体系的呈现往往是相反的.动量是最早被提出的基本力学概念之一,和力的概念几乎是同步发展的,早于牛顿运动定律.而动量守恒的观念又是先于动量的概念而产生.笛卡尔最早在他的《哲学原理》中提出:上帝创造物质时就赋予其各部分一个初速度,并将其保存在宇宙之中.虽然每个被推动的物体运动会变化,会时多时少,但总的看来却是一个永不增减的量.这就是动量守恒定律的滥觞.先提出守恒的设想,然后研究这守恒的东西究竟是什么,再进一步由牛顿运动定律定义什么是质量,进而给出了动量守恒定律的精确表达.这就是人类探索未知世界的真实路线图.可以说目前人教版教材的编写逻辑,就是从这儿得到的启发: “动量守恒定律”这节课被安排在人教版教材选修3-5第16章第3节,是放在“探究碰撞中的不变量”和“动量和动量定理”之后.纵观这一编排顺序,教材首先让学生通过科学探究,让学生经历问题的提出、猜想、验证等环节,体验动量守恒;其次由第一节课的探究,明确对动量这一概念的研究,并挖掘这一概念的力学相关规律——动量定理;最后从牛顿运动定律入手,从理论推导出动量守恒定律,并应用这一规律解决一些实际问题.不难看出编写者希望能让学生在课堂上逻辑化、真实化地从认知事物的最基本层面建构动量守恒定律.
2 教材呈现的逻辑缺失
尽管教材编写者试图让教材的呈现更体现逻辑感,但在“动量守恒定律”这一节内容中,仍然存在着一些以知识体系化代替真实逻辑化,导致逻辑链缺失的情况,主要表现在以下几个方面.
(1) 本节课在没有交代任何背景知识的情况下,首先直接给出“系统、内力和外力”的概念.“系统”概念的提出是因为碰撞问题研究的对象是两个(或多个)物体,但是为什么需要把物体的受力分为内力和外力呢?这其中有什么必然因素吗?教材中完全没有给出解释,所以导致学生对这一概念的来龙去脉不知其所以然.
(2) 在研究动量守恒定律的理论推导时,教材中直接提出“现在从牛顿运动定律的角度考查这个问题”,显得比较突兀,学生只是在教材这一主导下,按照预先设置好的路径将推导过程完成了一遍,这只能让学生知道:哦,这条路这么走是通的.但是为什么要走这条路,走上这条路时我们可能会遇到哪些问题,可能要用到哪些工具等等,这些都没有经过深究的问题让学生在探究的路上充满了疑惑.
(3) 对于动量守恒定律的条件,教材中提到“通过几代物理学家在实验上和理论上的分析、探索与争论,人们…形成了这样的共识,如果一个系统不受外力,或者所受外力的矢量和为0,这个系统动量保持不变.”这样的表述直接给出了动量守恒定律的条件,而没有指明这个条件由来.动量守恒定律既然是从牛顿运动定律的基础上分析证明得到的,那么这个条件也必定有其理论上的源头,这理应属于在高中生理解能力范围之内的学习内容,可是教材中没有给出动量守恒条件的说明,学生的认知链在此处被破坏.
(4) 动量守恒定律的近似条件是系统所受内力远大于外力,这是通过教材对一道例题的分析中给出的,如果说“若系统所受外力矢量和近似为0,系统动量近似守恒”这种说法学生还是能够接受的话,那么教材中的“外力远小于内力,可以忽略”就让学生充满了疑问,为什么外力是否可以忽略需要去和内力去相比较呢?内力的大小在动量守恒中为什么会扮演着如此重要的角色?这一点教材同样没有明确说明,这也是不符合学生认知逻辑的.
3 对追寻动量守恒定律的逻辑化处理
对动量守恒定律的追寻探究不应该只是教师为学生预设的一条规定路径,教学的设计不应仅仅让学生作为旁观者将整个探究过程目睹了一遍而已.教学过程更应该是教师为孩子构架的攀爬阶梯,教学设计的目的,是让学生在某种程度上经历这真实的探索,而非简单地在头脑中被强行注入异化的知识.基于这样的考虑,追寻动量守恒定律的过程可按照如图1所示的思维导图展开.
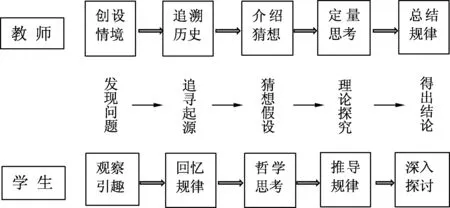
图1
3.1 发现问题
(用摄像探头投映演示)牛顿摆的碰撞实验,分别做单球释放、双球释放、两侧同数量球释放,两侧不同数量球释放等实验,让学生观察其中的神奇现象,引发学生对这些现象背后原理的思考.
3.2 追寻起源
力与运动关系的正确表述,是首先由伽利略提出的:若不受摩擦影响,物体具有某一初速度,它将永远保持这一速度运动下去,运动不需要力的维持.
但是这个结论的意义在当时并没有引起人们太多重视.因为在伽利略时代,力本身都是一个十分混乱而没有明确的概念.而自然界中物体间的碰撞、打击,倒是日常人类生活中最普遍、最直观的现象.研究物体与物体间在碰撞后的情况,才是最有现实意义的.所以人们对这类现象的观察、研究自然是最多的.人们想迫切地知道,两个物体碰撞后它们的运动会如何呢?
问:一个球撞击另一个静止在轨道上的球,最后它们的结果会如何呢?(实验演示)
答:它们都会停下来,最终运动都消失了,这是生活经验.
问:伽利略的结论告诉我们的是这样吗?运动会消失吗?
答:好像不应该会停止运动.
3.3 猜想假设
对于运动会否消失的问题,笛卡尔的观点更具哲学意味:上帝之所以创造了宇宙空间,就是为了能够把运动放入其中.运动一旦置于空间中,上帝任其自然进行而不干涉.宇宙中所有物质的运动总量必然是个恒定不变的常数,只是对于局部来说会有增有减.
这样的结论依赖于笛卡尔对上帝只创造规则,不干涉规则以及宇宙永恒不变的信念,因此思辨性成分居多,没有具体用实验或理论证实.但是这个思想为后人的研究指明了方向.
3.4 理论探究
3.4.1 牛顿理论的定性探究

图2
牛顿是集所有前人对力与运动研究成果的大成者,其最重要的成就就是牛顿运动定律.当具备了这样的工具后,就能帮助我们脚踏实地地研究笛卡尔的猜想了.如图2所示,光滑水平面上有两个小球,其中球2静止,球1以某一初速度向球2碰撞.
问:球1碰到了静止的球2后,它的运动会消失吗?
答:球1受到向后的撞击力,产生反向的加速度,于是会呈现3种可能,可能没有消失(继续前进或后退),也可能运动消失(球1停止了下来).
问:如果球1停下来了,运动是不是就此消失了呢?
答:不能只看球1,还要看球2.根据牛顿第三定律,球2受到了向前的撞击力(反作用力),产生向前的加速度,于是获得了速度,再根据牛顿第一定律,获得速度的球2将永远以这个速度运动下去,运动没有消失.
经过上述理论分析后,我们就能得到碰撞后物体的运动不会消失的肯定结论.
3.4.2 牛顿第二定律的定量探究

图3
若要深入讨论两球后继的运动情况,必须借助牛顿第二定律的精确定量性,对其进行受力分析,并给出数量关系,如图3所示.对球1有
F21=m1·a1,
(1)
再研究球2,
F12=m2·a2,
(2)
3.4.3 牛顿第三定律的纽带连接
在分别分析完两个物体的受力后,我们不难注意到这两者之间的纽带——牛顿第三定律,并且在其中有着比较特殊的3个关系:作用力F21与F12等大、反向、同时作用,因此由(1)、(2)式可得
(3)
整理后得
m1v1+m2v2=m1v1′+m2v2′.
(4)
3.5 得出结论
(4) 式体现的是运动在碰撞前后的某种守恒,这个守恒量就是动量mv.而这一点通过本章第一节的定量实验探究已经得到相应的结论,碰撞过程中的不变量就是mv.于是实验和理论都指向了同一点,那就是碰撞的过程中两个物体的总动量守恒.
4 对分析动量守恒定律条件的逻辑化处理
4.1 动量守恒定律条件的得出
通过前面的理论分析,我们知道了两个物体若是碰撞后,总动量是不变的.但是在我们的实际生活中,遇到的情况却往往是:两个小球在水平面上碰撞后,最终全都会停止,总动量变为0.
问:是什么原因导致两个物体的总动量不守恒?
答:水平面粗糙,物体受到了摩擦力.
问:为什么受摩擦力,两个物体的动量就不守恒呢?

图4
重新审视刚才的牛顿运动定律的理论分析,并对两个小球进行有摩擦力情况下的受力分析,如图4所示,当两个球都受摩擦力时,式(1)、(2)会变成
(5)
(6)
在这种情况下,(5)、(6)两式不再相等,(3)式不再成立,也就无法得到(4)式,故总动量不守恒,这样看来不是在所有情况都是动量守恒的.
问:那什么条件下动量会守恒呢?
答:不受摩擦力.
问:但是不受摩擦力可能只是在这个特定问题中的特定情况,不是本质原因.那么动量守恒普适性的原因究竟是什么呢?再重新观察图3,总结原因.
答:合力为0.
问:可是球1和球2的合力都不是0,请大家再次观察.
答:尽管球1和球2的合力都不为0,但是两个物体总的合力为0.
研究物体的碰撞,最重要的意义就在于,把目光从孤立的单个物体转投向整体分析.我们需要引导学生要跳出以往牛顿运动定律解决问题带来的视角狭窄的问题.牛顿运动定律总是带有很强的因果律效应,“力”与加速度的地位严重不相等,前者决定后者.而生活中却是大量的活生生的,公平视角下的,物体与物体彼此之间的碰撞,不是孤立地谁决定谁,而是彼此共存共变.这样我们的世界就被放置到了宇宙的宏观叙事视角下,于是系统和守恒自然落入到我们视线的范围内,对于碰撞后动量守恒的问题,也应该放在考虑系统的大框架下,而不是单个物体的情况.
当我们把这两个物体合在一起讨论时,这两个物体我们就称之为系统,系统不仅限于2个,可以是3个、4个,甚至包容万物.在图3中系统总共受6个力,其中碰撞作用力F12和F21是系统内部物体之间的作用力与反作用力,我们称为内力.由于内力必定是成对出现的作用力与反作用力,彼此等大反向,所以它们施加于系统的合效果必为0,因此内力不影响系统动量的守恒.两个物体所受的重力和支持力,是系统受到外界对系统施加的力,我们称为外力.由于系统内力和始终为0,那么只要系统外力矢量和为0,系统总的合力就为0.于是系统所受合外力为0,就成为了动量守恒的决定性因素,这就是系统动量守恒的条件.
4.2 动量守恒定律近似条件的得出
人教版教材选修3-5第14页的例题1中,在讨论两节车厢碰撞动量是否守恒时,教材中给出了这样一段话“系统所受的外力有:重力、地面支持力、地面摩擦力和空气阻力.重力与支持力之和等于0,摩擦力和空气阻力远小于碰撞过程中发生的内力,可以忽略.因此,可以认为碰撞过程中系统所受外力的矢量和为0,动量守恒” .这样的表述显然不够严谨,为什么可以这样近似?这与外力与内力的大小比较又有什么关系呢?这些都必须在前面的理论推导过程中追根溯源.
根据图4分析可得,(5)式左边为F21+f1,(6)式左边为F12-f2,无法等价为(3)式.但是如果F21和F12远大于摩擦力的话,那么(5)、(6)两式是可以近似相等的.所以不是看外力的绝对大小,而是看外力与内力的相对关系.在上述教材的例题中火车车厢所受的摩擦力其实是非常大的,不能简单地忽略.但也并不因为摩擦力很大而系统动量不守恒,而是因为摩擦力和更大的撞击内力相比小得多,符合了前面的理论推导的系统动量守恒的近似条件.经过这一系列的讨论之后,最终可以总结为:当系统所受合外力远小于内力时,系统近似可认为动量守恒.
笔者通过对“动量守恒定律”教学的重新设计,意图就在于厘清课堂教学过程中的真实逻辑路径,其正是回应了物理学科核心素养“物理观念”中对“运动观念、相互作用观念”的重视,回应了“科学思维”中“能正确运用科学思维方法,从定性和定量两个方面进行科学推理、找出规律、形成结论,并能解释自然现象和解决实际问题”的要求.物理学科核心素养的内在本质不仅仅是向学生传授缜密的科学知识体系,更应该是对学生理性思维的培养和拓展,这也是我们对于课堂教学设计的重要内核.

