异方差G-Q检验方法的改进
刘 明,黄恒君(兰州财经大学 a.甘肃经济发展数量分析研究中心;b.统计学院 甘肃 兰州 730020)
一、问题的提出
在计量经济学模型中,如果出现异方差问题,则会对模型的估计、检验及应用带来一系列不良后果,因而如何发现异方差是计量经济学建模过程中所关注的一个重要问题。计量经济学模型中异方差问题的本质是随机项的方差随着个体的变化而出现了变化,基于这一本质,自20世纪50年代以来设计了诸多异方差的检验方法,这些检验方法因样本数据和模型形式的差异而各有不同、各具特色,但都是基于总体模型的异方差理论并结合现有样本信息而设计的,也都是根据样本信息对总体异方差状况进行推断。在推断过程中,如何将总体信息与样本信息进行有效衔接是异方差检验设计的一个重要内容。传统的异方差检验方法整体上实现了总体信息与样本信息进行有效衔接,但相关文献对此并没有给予清晰的表述;同时,也有检验方法对样本信息的使用不够到位,仍有进一步开发的空间,例如戈德菲尔德—匡特异方差检验(Goldfeld-Quandt Test,G-Q检验)。基于此,本文拟结合G-Q检验针对异方差问题开展如下研究:
第一,阐释异方差检验中几个易被忽略的样本与总体关系的问题,以更清晰地展示异方差检验的基本原理。本文将阐释的问题是:模型样本残差的平方为什么可以用来表示随机干扰项的方差?异方差为什么被假定为受解释变量的影响或与解释变量相关?这些问题看似简单因而不容易被人们所关注,而且在国内外已有的计量经济学文献中鲜有对这些问题进行讨论和阐释,尽管这些问题在异方差检验中都是既定的观点和做法。鉴于此,本文将论证之并展示其合理性,以使人们更容易理解现有异方差检验的思路,更重要的是为后文实现G-Q检验的改进做出准备。
第二,对G-Q异方差检验方法展开讨论,并在多元回归模型的基础上综合开发运用样本信息,以实现对G-Q异方差检验方法的改进。首先,将讨论G-Q检验中所用到的F检验是否必须是单侧检验,这是后文中有关改进的G-Q检验所必须讨论的一个问题;进一步,将传统的一元线性回归模型的G-Q检验方法向多元线性回归模型推广,实现该检验方法的改进,这是本文的重中之重。
本文研究设计的多元线性回归模型的G-Q检验方法属于检验设计的创新,解决了传统G-Q检验不能实施或不便于实施多元回归模型的异方差检验问题,而检验逻辑和检验统计量均遵循了原有的G-Q检验方法。
为保证研究的连贯性和完整性,首先对一般的异方差G-Q检验方法做简单介绍[1]。G-Q检验是一种发展相对成熟的异方差检验方法,在国内外的诸多计量经济学教科书中均有详细介绍,它是1965年由Goldfeld和Quandt创立的。G-Q检验主要适用于检验递增型的异方差,该检验用到的统计量是服从F分布的统计量,检验原假设为“随机干扰项是同方差的”,备择假设为“随机干扰项存在递增型异方差”,具体的检验步骤为:
第一步,按照解释变量xi的观测值由小到大的顺序对样本点进行排列。
第二步,将排列在正中间的c个样本点删去,将剩下的n-c个观测值划分为容量相等的两个子样本,每个子样本的容量分别为(n-c)/2,其中的一个子样本是xi观测值的较大部分,另一个是xi观测值中较小的部分。

第四步,建立统计量:
可以证明
第五步,进行检验判断,即对于给定的显著性水平α确定相应的临界值Fα,若F>Fα则拒绝“随机干扰项是同方差的”的原假设,认为模型存在递增型异方差;若F≤Fα则保留原假设,即模型随机项不存在递增型异方差。
二、关于异方差检验的两个基本问题的讨论
异方差的检验方法有多种,除了本文将要讨论的G-Q检验之外,还有多种检验形式,这些检验方法一般都有各自的使用条件,具体可参见相关计量经济学教科书,这里不再赘述。在诸多的异方差检验方法中,一般都暗含着两个基本假设条件,即模型残差的平方序列是随机项方差的估计以及异方差和模型解释变量有关系(自回归条件异方差检验没有遵循这一假定)*需要强调的是:这是异方差检验过程中隐含的一个假定而不是异方差的定义,异方差的定义一般表述为“随着个体的不同,随机误差项的方差不确定”,异方差的定义强调个体变化对随机项方差的影响。当然,这种定义是在理论上的,现实中还是需要借助于样本信息来识别异方差。。如何认识和理解异方差检验中的这两个隐含的假设条件,是本文讨论的第一组问题,也是后续研究的基础。
(一)如何理解用残差平方表示随机项方差
考虑如下形式的计量经济学模型:
yi=α0+α1x1i+α2x2i+…+αmxm i+μi
(1)
其中随机干扰项μi被要求满足高斯假定,由此可知μi是一组独立同分布的正态变量。通常情况下,认为μi的方差Var(μi)为参数σ2。如果给定一组样本数据,利用OLS法即可得到式(1)的样本模型:



(二)为什么异方差被假定为和解释变量相关
在检验异方差的G-Q检验方法中,一般假定随机干扰项的异方差是由解释变量引起的,至少是和解释变量相关的,这一假定也是其他几类异方差检验方法的基础,例如布罗斯-帕甘检验[2]、怀特检验[3]、帕克检验[4]以及国内相关学者的研究成果等[5],但经典文献中并未提及假定异方差和解释变量相关的原因,人们对于这一问题的一般理解是:解释变量一般为已知的外生变量,因而假定异方差和解释变量相关,不仅有助于找到异方差的变动形式,还能为解决异方差问题提供基础。诚然,确定了异方差和解释变量之间的关系,无疑是为找到异方差问题的解决途径而奠定了基础,但这并不能成为假定异方差和解释变量相关的理由。笔者通过分析研究,认为至少存在如下两个方面的原因使异方差和解释变量相关这一假定是合乎现实的:
其一,模型的设定要求。如果模型(1)的异方差Var(μi)是由模型之外的因素所引起的,不妨假设为zi,即Var(μi)=f(zi),则必有:
Var(yi)=f(zi)
即模型外因素zi引起了被解释变量yi的波动,亦即yi的变动至少部分上可以由zi解释,这意味着模型(1)在设定过程中遗漏了重要的解释变量zi,从而造成了模型的设定误差,而模型的设定误差在构建计量经济学模型过程中是不被允许的。换言之,不可能存在模型之外的因素影响异方差,否则就会造成模型的设定误差,即存在设定误差的模型是不符合研究要求和实际需要的模型,此时模型本身就是错误的。
其二,个体异质性的本质属性。个体异质性是模型产生异方差的重要原因,对于纯随机因素造成的个体异质性一般不会引起模型的异方差,因为纯随机因素对于每一个体产生的影响是相同的。一般情形下,个体的异质性主要是由个体自身属性决定的,而这些自身属性就是由该个体的每一解释变量体现出来。因此,由于个体异质性所产生的模型异方差必然和解释变量相关。
另外,数据的观测误差也可能造成模型的异方差。如果数据的观测误差属于纯随机误差,则一般不会造成异方差后果;如果观测误差属于系统性误差,则容易造成异方差,但这是由于数据质量问题造成的,此时的异方差属于样本现象,不在本文议题之内。
三、G-Q检验中的F检验再设计
将目标对准异方差G-Q检验。传统的G-Q检验是通过构建F统计量而完成的异方差检验。事实上,G-Q检验的F统计量是通过下述路径所构造的:
即残差平方和与对应的随机干扰项方差之比形成卡方分布,在独立性条件下即可构建F统计量:



综上认为,G-Q检验可以按照不同的检验目标来进行,这些检验目标包括“模型是否存在递增型异方差”、“模型是否存在递减型异方差”以及“模型是否存在异方差”等,检验的统计量依旧都是F统计量,具体包括了“单侧检验”和“双侧检验”两种不同的检验判别模式。
四、基于多元线性回归模型的G-Q检验的改进
对于多元线性回归模型,实施G-Q检验时就会面临这样的一个问题:在对样本点进行排序时应该以哪一个解释变量为依据?有人建议按每一解释变量的顺序将样本点进行多次排序,并进行多次检验,由此诊断模型的异方差性。诚然,这种处理方法是可靠的,可以通过这种方法检测出模型是否存在异方差以及何种形式(递增型或递减型)的异方差,但进行多次的G-Q检验过于繁琐,工作效率降低,因而不为人们接受。龚秀芳建议根据解释变量的样本第一主成分来对样本点进行排序[6],但这种方法仅考虑了解释变量之间相关性的信息,并没有体现解释变量与异方差之间的相关性,同时这种方法在操作起来也较为复杂。因此,笔者针对多元线性回归模型的异方差G-Q检验的样本排序问题,寻找可靠的排序依据,并确保检验方法简单易行。
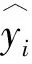
第一,易于判断递增型或递减型的异方差。针对模型(1),其样本拟合结果为:


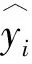
yi=α+βxi+ε
其样本拟合值可表示为:

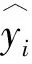
五、统计模拟与案例
(一)统计模拟
为论证第四部分中所提出的使用被解释变量的拟合值作为样本点的排序依据,进而完成多元线性回归模型的G-Q检验方法,并对此方法进行统计模拟实验。
1.数据生成机制。设定3组样本变量x1、x2、x3,全部是均值为0、方差为1的且服从正态分布的变量,样本容量为201。考虑到3个变量间的相关性可能会对检验结果造成影响,因此在生成数据时额外设定了两两之间的皮尔逊相关系数。被解释变量y的生成机制是:
y=100+x1+x2+x3+μ
其中μ为零均值的正态随机误差项,设定随机项的形式为:
显然,这类随机项的形式极易产生异方差问题,且异方差和x2有关,其中ξ为服从标准正态分布的、相互独立的随机变量。
2.异方差检验。设定变量x1、x2、x3两两之间的相关系数依次为0、0.1、0.2、0.3、0.5、0.7、0.8、0.9*事实上,为保证本文研究的严谨性,笔者拟合了皮尔逊相关系数为0、0.05、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、0.95等12种情形,在不影响科学性的前提下,删除了其中的部分拟合结果,以节约篇幅。另外,为简化模拟过程,假设解释变量之间的相关系数相同,这不会影响到模拟的科学性和有效性。,并按上述机制生成数据,根据所生成的数据分别进行传统的G-Q检验和本文设计的G-Q检验。检验过程中剔除样本点的个数为41,并设定拒绝原假设的概率为10%,因而F检验的临界值分别为F0.05(76,76)=0.684 048 535,F0.95(76,76)=1.461 884 571。为详细展示检验结果,首先在各相关系数下仅生成一组数据,这8组数据的G-Q检验结果如表1所示。
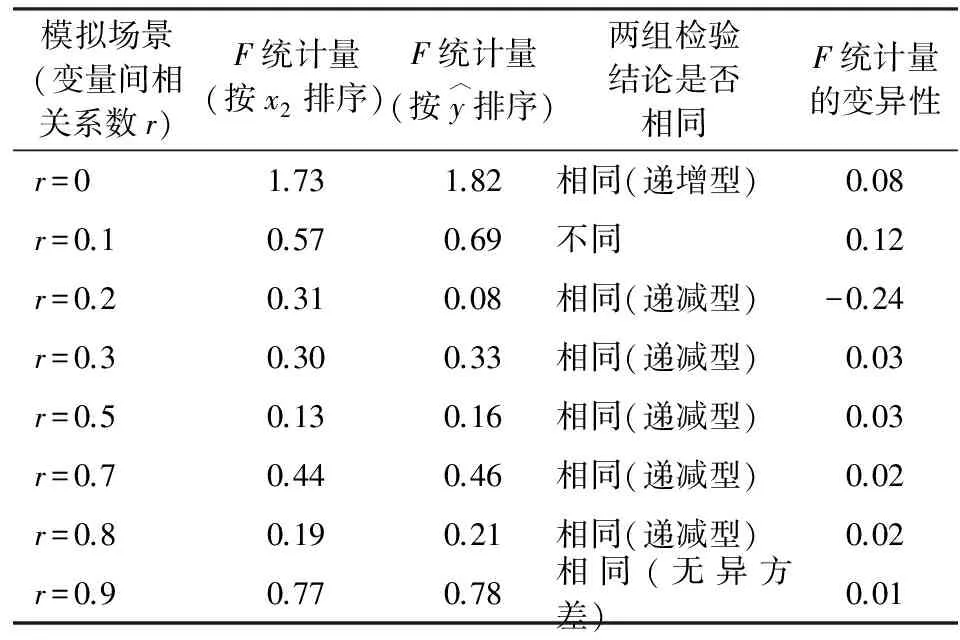
表1 模拟数据异方差G-Q检验结果表(1次模拟)
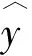
进一步,在每一个相关系数场合下进行了10 000次数据模拟实验,并利用模拟数据进行了异方差检验,检验结果信息见表2。
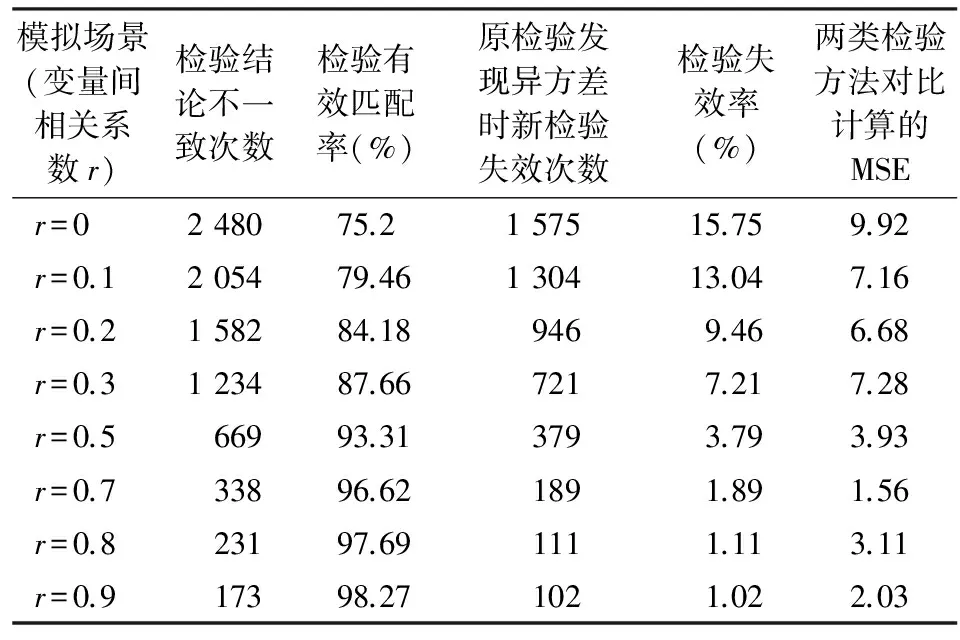
表2 模拟数据异方差G-Q检验结果(10 000次模拟)
由表2可看出,当解释变量之间不相关(相关系数为0)时,在10 000次模拟中,新检验方法和原检验方法所得出的检验结论不一致的次数达到2 480次,两类检验结果的有效匹配率(相同的比率)仅为75.2%,相对较低。随着解释变量间相关性的增强,检验结论不一致的次数在减少,即检验结果的有效匹配率在增加;当相关系数为0.3时,有效匹配率就达到了87.66%,这种两类检验结果的匹配率随着解释变量间相关系数的增加而增加;当相关系数为0.7时,这种匹配率就达到了96.62%。进一步,研究分析“原检验发现异方差时新检验失效次数”和“检验失效率”,这两个数据直接反映了本文设计的检验方法的可靠性。不难发现,虽然在解释变量不相关时检验的失效率较高,达到了15.75%,但随着解释变量相关性的增强,检验失效率在快速下降;当解释变量相关系数达到0.2时,拟合结果即显示检验失效率降到了10%以下;当相关系数为0.5时,检验失效率降到了3.79%。另外,为比较两类检验方法的综合差异性,在相同的相关系数下所生成的10 000组随机数据基础上计算出了两类检验方法各自的F统计量值,并计算了F统计量的平均离差平方和,即MSE。可见,随着解释变量间相关性的增强,MSE也在减小,即两类检验方法的检验结论越来越接近。


(二)案例分析
1991年,美国环境保护署在发布的一份报告中给出了81辆汽车在每加仑汽油里程数(MPG)、发动机马力(HP)、驾驶空间立方英尺数(VOL)、最高时速(SP)和车身重量(WT,单位为100磅)等方面的数据[7]404-406,构建用于研究汽车行驶效率的回归模型,模型形式设定如下:
MPGi=β0+β1HPi+β2VOLi+β3SPi+
β4WTi+εi
(2)
利用81辆汽车数据估计出的模型为:

1.252 8SPi-1.855 3WTi
通过使用Breusch-Pagan-Godfrey检验、White检验和Harvey检验(模型的其他检验信息略去)对此模型进行异方差检验,均发现模型存在异方差,检验结果如表3。

表3 模型异方差检验结果表
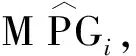

图1 MPGi、拟合值及残差平方序列图

表4 新G-Q检验结果表
检验所用F统计量服从第一自由度和第二自由度均为25的F分布。由此可以看出,使用被解释变量的拟合值对样本进行排序,可以顺利实施并完成G-Q检验。
[1] Goldfeld S M,Quandt R E.Some Tests for Homoscedasticity[J].Journal of the American Statistical Association,1965(6).
[2] BreuschT S,Pagan A R.A Simple Test for Heteroscedasticity and Random Coefficient Variation[J].Econometrica,1979(9).
[3] White H.A Heteroscedasticity Consistent Covariance Matrix Estimator and a Direct Test of Heteroscedasticity[J].Econometrica,1980,48(5).
[4] Park R E.Estimation with Heteroscedastic Error Terms[J].Econometrica,1966,34(10).
[5] 王佐仁,徐生霞.蒙特卡罗方法下线性模型的异方差性检验方法[J].统计与信息论坛,2016(11).
[6] 龚秀芳.戈德菲尔德-匡特检验的推广[J].数理统计与管理,2005(1).
[7] 古扎拉蒂.计量经济学基础[M].北京:中国人民大学出版社,2005.
——《计量经济学方法论研究》评介

