行进间对准参数误差灵敏度分析
王立兵,赵 圆,温 习
(1. 中国电子科技集团公司第五十四研究所,石家庄 050081;2. 卫星导航系统与装备技术国家重点实验室,石家庄 050081;3. 中国人民解放军63961部队,北京 100012;4. 天津航海仪器研究所,天津 300131)
捷联惯导系统已经广泛应用于各类载体的实时导航需求,利用陀螺和加表的输出信号,通过求解非线性微分方程进行导航解算,为载体提供位置、速度和姿态航向信息。精确的初始对准结果是保证后期导航信息精度的重要条件。
文献[1-2]采用基于最优化的方法,将姿态阵分解成两个时变姿态阵和一个常值姿态阵,构造矢量观测,估计该常值阵,完成了捷联惯导系统的行进间对准。因为这是一种基于最优化的对准方法,需要利用绝对位置和地速来构造观测矢量,只能靠卫导信息来辅助完成,而里程计信息只能提供载体系内相对位置和速度信息。所以这种方法无法应用在里程计辅助的车载惯导系统上。文献[3-6]解决了这一问题,将比力方程表示到载体系内,通过积分加速度信息来构造观测矢量,再利用最优化的方法完成里程计辅助的捷联惯导系统的初始对准。另外,受载体恶劣动态的影响,陀螺和加表的误差会在这种应用场景中产生一定程度的影响,文献[7-9]讨论了惯性卫导组合导航系统中,陀螺、加表误差对于滤波器的动态影响程度。文献[10-11]实现了里程计辅助的行进间对准。
在实际设备跑车实验中,有时会出现滤波器的误差状态估计曲线振荡,收敛缓慢的现象。有必要针对这一现象,结合实际车辆运动状态和惯性测量组件的参数误差的特点,分析问题的根源。本文从惯导系统的误差方程出发,得出了航向估计稳态误差与各项参考信息精度和各项惯性元件精度之间的定量关系,在半实物仿真基础上,验证了各个参数误差对航向对准精度的影响,为惯性设备原理方案设计与实际系统调试工作提供指导。
1 行进间对准算法
行进间对准利用惯导系统与里程计组成组合导航系统,采用卡尔曼滤波器估计惯导系统的姿态角误差,完成车辆动态过程中的航向对准。
选取了21维状态变量,分别是惯导系统误差状态(包括3个姿态角误差φ、3个速度误差 δvn、3个位置误差δp、3个陀螺常值误差ε和3个加表常值误差∇)和里程计定位系统误差状态(里程计定位误差δpodo、俯仰安装偏角误差δαθ、方位安装偏角误差δαψ和里程当量误差δKodo)写成向量形式为:

惯导里程计组合导航的误差状态转移矩阵如式(1)所示,包括惯导误差方程和里程计定位误差方程两部分:

式中惯导系统误差方程如式(2)所示:
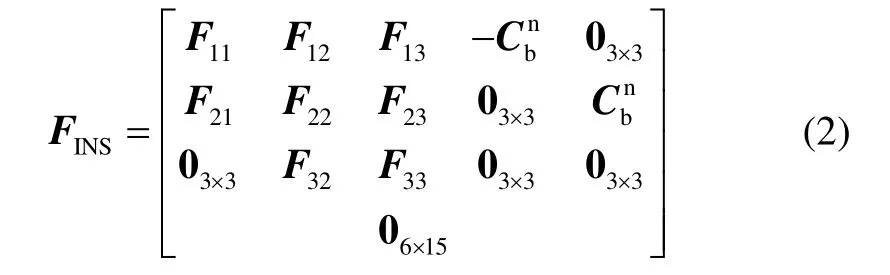
其中,各分块矩阵可参考文献[10]。
里程计定位误差方程为

式中各分块矩阵为:

其中,vn为导航系内的里程计速度,ΔS为t时间odoodos段内的里程计位移增量。量测方程为:

2 参数误差灵敏度分析
此处的参数包括里程计相关参数和惯性元件相关参数。里程计相关参数影响了量测信息的准确性,而陀螺、加表相关参数影响了系统解算量的准确性。要定量分析这些参数误差对于航向对准的影响程度,需从惯导系统的误差方程入手,找到航向估计的稳态误差与上述参数误差的解析关系。
关于速度误差和姿态误差的矢量方程为

为了便于推导,将式(4)写成如下分量形式:


由式(5)整理移项,得到φNn的表达式为:

再由式(6)整理移项,得到φEn的表达式为:
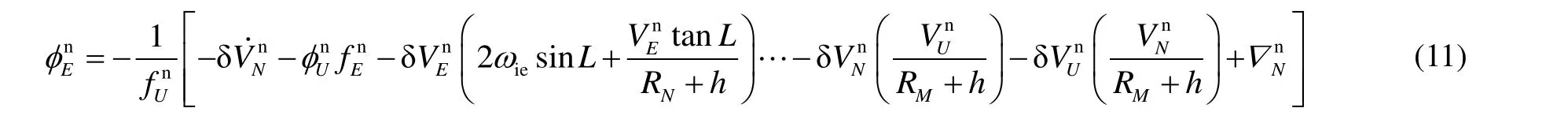
对式(11)两边微分,得到φEn的表达式为:

由式(7)移项整理,得到φUn的表达式为:

再将式(10)(12)代入式(13),消去φEn和φNn项,得到φUn关于 δVn、εn、∇n的表达式为:

将φUn项移到等式左边,等式右边为 δVNn、δVEn、δVNn、δVUn、δVEn、δVNn、δVUn、∇Nn、∇En、εEn的多项式,得:

假设载车动态行驶速度不超过 120 km/h且车辆近似水平匀速行驶。则近似计算式(15)中各项误差的系数可知,VnR≈5×10-6rad/s,ωie≈7×10-5rad/s,显然速度引起的ωenn幅值约为ωie的114。由匀速可知近似为零,
综上条件,忽略上述小量及其高阶项,可得化简后的航向误差与参数误差的表达式为:

进一步化简式(16),得:

等式右边第一项可认为是北向参考速度误差导致的ωn的计算误差,使得计算平台系绕东向轴的缓en慢旋转,与东向陀螺常值误差等效,近似计算可知北向参考速度误差为 0.3 m/s时,约可等效为 0.01(°)/h的陀螺常值误差;等式右边第二项可认为是等效北向加表斜坡漂移导致计算平台系绕东向轴的缓慢旋转,也与东向陀螺常值误差等效,近似计算可知等效北向加表斜坡漂移为15 μg@300 s时,约可等效为0.01(°)/h的陀螺常值误差;对于等式右边第三项,设∇En为 50 μg,则其对应的航向误差约为 10″,可忽略不计;等式右边第四项为陀螺常值误差。
3 半实物仿真分析
针对第2节中的各项参数误差分别进行仿真验证。本文采用实车动态对准中惯性级惯组的原始数据进行半实物仿真验证,人为添加相关误差特性,得到仿真结果与第2节中的理论计算结果进行对比分析。
采用准确参数的动态对准结果如图1和图2所示。

图1 载车运动状态Fig.1 Dynamic states of vehicle

图2 卡尔曼滤波器误差状态估计Fig.2 Estimation of Kalman filter error states
观察图1速度曲线,可知车辆行驶最大速度出现在前200 s,幅值约为30 m/s,此后做了大于90°的转弯机动,经过车辆一段时间的机动,滤波器对于姿态和航向误差的估计趋于收敛,如图2所示。
3.1 里程当量误差
人为添加 1%的里程当量误差,引入约为 0.3 m/s的速度参考误差,进行动态对准仿真,结果如图3所示。
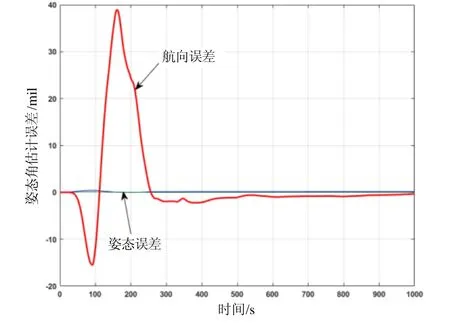
图3 增加1%里程当量误差后的姿态角估计误差Fig.3 Estimation errors of attitude angles with 1%odometer scale factor error
图3与图2对比可见,航向误差估计在前200 s的时间内振幅明显增大,与人为添加的里程当量误差引入的参考速度误差有关,但经过一段时间的车辆行驶过程,由图4的里程当量误差估计曲线可知,人为添加的误差被准确估计出来,最终动态对准的结果与未添加里程当量误差时的结果一致。

图4 增加1%误差后的里程当量估计曲线Fig.4 Odometer scale factor estimation curve with 1% error
上述分析验证了关于参考速度误差对于航向对准的影响作用。进一步分析发现,行进间对准算法设计中已经将可能引入参考速度误差的里程当量误差作为卡尔曼滤波器误差状态向量的一个分量包含进去,在惯导里程计组合过程中,该误差能被准确辨识,从而消除参考速度误差,最终保证航向对准的稳态结果不受里程当量误差影响。
3.2 等效北向加表斜坡漂移
人为添加15μg@300s的等效北向加表斜坡漂移,重新进行仿真实验,结果如图5所示。增加等效北向加表斜坡漂移以后,整个动态对准的滤波器收敛过程基本与准确参数的过程一致,但整体上移了约1 mil,这就验证了等效北向加表斜坡对航向对准稳态误差的影响程度。
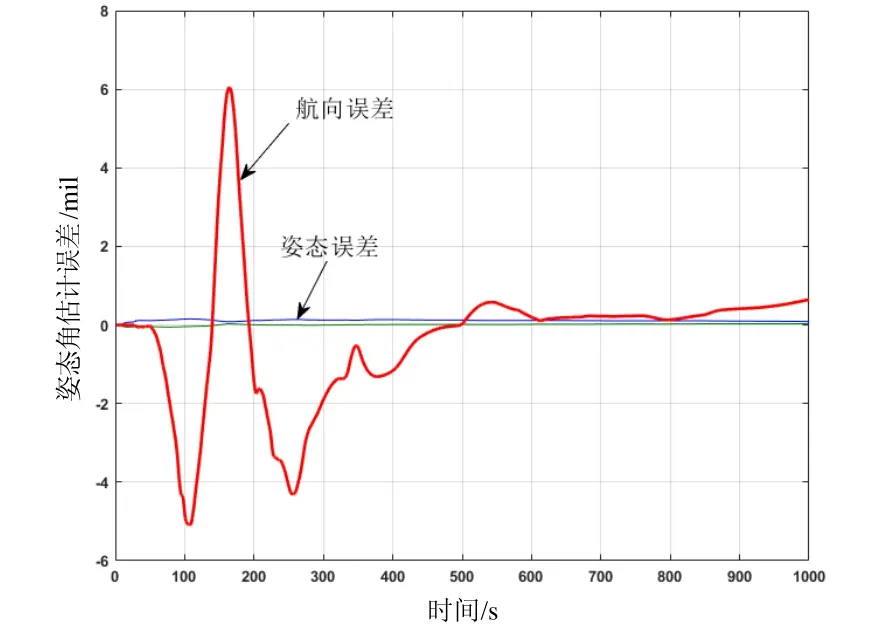
图5 增加等效北向加表斜坡漂移的姿态角估计误差Fig.5 Estimation errors of attitude angles with north accelerometer ramp drift
人为添加x轴加表常值误差80 μg,在车辆运动过程中发生转弯机动过程,由于x轴加表和y轴加表自身常值误差不一致,等效北向加表误差将会发生暂态变化,产生了短暂的等效北向加表斜坡漂移,对添加误差后的数据进行仿真分析,结果如图6和图7所示。

图6 增加x轴加表常值误差80 μg的姿态角估计误差Fig.6 Estimation errors of attitude angles with 80 μg ax bias

图7 增加x轴加表误差80 μg的加表误差估计曲线Fig.7 Estimation curves of accelerometer biases with 80 μg ax bias
由图7的加表常值误差估计曲线可见,x轴加表的常值误差估计结果约为80μg,与人为添加的误差一致,但从图6可见航向误差估计曲线的收敛过程明显发生变化,与图2相比在车辆进行转弯机动之后,滤波器振幅增加到20 mil,然后缓慢趋于收敛,这一暂态波动现象的原因就是引入x轴加表常值误差后,在车辆转弯后,等效北向加表误差发生了暂时的变化,也就是短暂的等效北向加表斜坡漂移,其对于航向误差的估计就会产生一定程度的扰动。这种现象如果出现在对准将要结束的时间段,则引起的航向误差估计大幅震荡的结果将导致对准精度降低,必须引起足够重视。
3.3 陀螺常值误差
人为添加0.01(°)/h的等效东向陀螺常值误差,对原始数据进行仿真分析,结果如图8和图9所示。

图8 增加0.01(°)/h等效东向陀螺漂移的姿态角估计误差Fig.8 Estimation errors of attitude angles with 0.01(°)/h east gyro bias

图9 陀螺漂移估计曲线Fig.9 Estimation curve of gyro bias
由图9的陀螺误差估计曲线可见,两只陀螺的常值误差估计曲线未发生任何变化,这是由于等效东向陀螺误差不可观测,所以无法反映到陀螺误差估计的状态上,但是从图8可见,最终航向对准误差发生了相应的改变,这与第2节中的对准误差分析结果一致。
4 结 论
由陆用惯性定位定向设备的里程计辅助行进间对准算法设计入手,经过对惯导误差方程的推导,得到了航向估计稳态误差与各项参考信息精度和各项惯性元件精度之间的定量关系。其中里程当量误差虽然可以引入参考速度误差,但是在卡尔曼滤波器工作过程中,作为其误差状态矢量的一个分量,里程当量误差被准确估计出来,进而避免了参考速度误差对航向误差估计精度的影响。
等效北向加表斜坡漂移对于航向对准精度的影响得到了仿真验证,定量关系与理论分析的结果一致。转弯机动引入的导航系内等效北向加表误差变化可视为暂时的北向加表斜坡漂移,可导致航向对准过程中的滤波器振荡和不稳定,这一现象在原理方案设计与系统实际调试过程中往往被忽略,如果不引起足够重视,则会严重影响航向对准精度。等效东向陀螺漂移的影响与理论分析得到的解析式一致。
理论分析结果与仿真实验结果证明了行进间对准过程中各参数误差与航向对准精度之间的定量关系,对惯性设备原理方案设计与实际系统调试工作具有参考意义。

