一种异类多传感器航迹关联新算法*

高晓利 ，李 捷 ，2

（1.四川九洲电器集团有限责任公司，四川 绵阳 621000；2.电子科技大学通信抗干扰国家重点实验室，成都 611731）

0 引言

随着计算技术的快速发展，数据融合也得到了飞速发展，并已广泛应用于目标跟踪、态势评估等军事和民用领域［1］。而航迹关联效果的好坏是数据融合正确性的前提和保证。

近年来，航迹关联的主要算法有加权统计距离检验法［2］、修正的加权统计距离检验法［3-4］、最近邻法［5］、k 近邻法［6-7］等，然而，在目标密集或相对位置较近的环境下，这些算法可能将导致较多的错误关联发生。为了解决错误关联问题，各国学者提出一类基于随机有限集的跟踪算法［8-16］，但算法复杂度较高，尚未用于工程。因此，针对传统最近邻域关联算法局部搜索特性和关联结果对阈值的取值精度的依赖，充分研究了异类多传感器航迹信息的特点，提出了一种基于异类多传感器航迹关联的新方法。

该方法首先进行基于专属信息的完美关联，其次进行基于共有信息的非完美关联，最后给出了冲突解决机制。该方法不仅具有严谨的数学基础，而且便于工程实现。数值试验表明，该方法与经典最近邻方法相比，该算法不论航迹分布状态是稀疏还是密集，该方法都具有较好的航迹关联结果。

1 预备知识

1.1 最近邻域算法

最近邻域法实质上是一种局部最优的“贪心”算法。该算法具有计算量小和强鲁棒性特点，简单而高效，特别适合实时性要求高的应用环境，是一种在实际数据融合和目标跟踪系统中被广泛采用的数据关联算法。

1.2 完美关联和非完美关联

假设每条目标航迹信息包含共有信息和专属信息两类，其中共有信息指不论哪种传感器建立航迹均包含的信息，如航迹点的经度、纬度、高度等；专属信息是特定传感器具有的信息，如ADS-B建立航迹所具有的24位地址码、数据链传感器建立航迹所具有的批号等。

所谓完美关联是指利用测量航迹中的专属信息进行匹配。如果专属信息完全，则可以直接输出完美关联的结果。

所谓非完美关联是指利用测量航迹中的共有信息进行匹配。非完美关联是在完美关联失败的情况启动。

1.3 航迹文件库

航迹库也称为历史航迹库，即在同一场景下，所有目标航迹的集合，其中每条航迹由航迹号、共有信息和专属信息组成。在所有目标航迹连续的条件下，航迹库具有以下特点：1）航迹编号具有唯一性；2）航迹信息随着场景运行不断更新；3）航迹信息由最近多个周期的关联结果组成。

2 航迹关联流程

2.1 完美关联

完美关联是航迹关联的第一步，指根据测量航迹中的专属信息与航迹库中的所有航迹进行匹配，其基本步骤如下：

步骤1：根据测量数据是否早于已有航迹的最新时间，删除冗余航迹。假设测量航迹数据时间为time_measure，已有航迹的最新时间为time_hisnew，如果time_measure＜time_hisnew，则认为该测量航迹是多余的，不进行后续处理；否则，实现非完美关联。

步骤2：判断航迹库中是否已经存在该测量航迹数据，并实现航迹库更新。如果已经存在，则找出该测量航迹在航迹库中的存放位置，以便将后续处理的结果在此位置上进行更新；如果不存在，则需要创建一个新的航迹，并加入到航迹库中。

步骤3：如果专属信息存在且正确，那么完美关联的结果总是正确的；否则，专属信息缺失或错误，采用完美关联处理之后，继续非完美关联处理。

2.2 非完美关联

非完美航迹关联是基于航迹共有信息，对已有综合航迹的多层筛选。其基本步骤如下：

步骤1：判断测量航迹先前是否已和已有的综合航迹中的一条航迹相关联。如果测量航迹和已有综合航迹关联成功，则判断先前的关联现在是否仍然有效，如果超过了关联有效门限，相关的航迹要进行合批/分批波门检测。如果关联仍然是有效的，就完成了航迹共有信息的非完美关联，并且不会进行后续处理。如果关联已经失效，则进行其他航迹是否相关的检测。

步骤2：利用航迹的不确定量判断航迹库中有哪些其他航迹落入被报告的航迹的不确定量的范围内。符合关联波门的航迹被记为候选关联航迹。

步骤3：从步骤2筛选所形成候选关联航迹中挑选出一条匹配度最高的航迹作为关联航迹。于是可以得出航迹关联处理的流程如下页图1所示。

3 航迹关联判决计算

航迹关联判决主要包含航迹协方差更新、航迹误差均值计算和航迹相关判决3部分。

3.1 航迹协方差更新

假设目标在三维空间中做直线运动，运动点迹由距离、方位和俯仰角组成，则航迹协方差矩阵是6*6矩阵，不妨假设为，则COV中的值随着新航迹点的加入而不断更新。假设COV中的元素的初始值为1，则更新步骤如下：

步骤1：计算传感器探测误差的Sigma因子。记跟踪距离误差、方位误差和俯仰误差的Sigma因子分别为SigmaRng、SigmaAz和SigmaEl，则其计算公式分别为：

式中，RngRand：距离不确定性，单位为 m；AzRand：方位不确定性，单位为°；SElRand：俯仰不确定性，单位为°；RngSysNoise：距离系统噪声，单位为m；AzSysNoise：方位系统噪声，单位为°；ElMultiPth：俯仰多径系数，无量纲；MlPth：多径系数的和，无量纲；ElBeamwidth：传感器波束俯仰宽度，单位：°；DiffChannleSlop：传感器的高差斜率，无量纲，一般取值为1.2分别为距离分辨率平方、方位分辨率平方和俯仰分辨率平方。

以上参数全部是传感器的性能参数或者可根据传感器的性能参数计算得出。

步骤2：依据运动方程实现协方差矩阵更新。

其他元素的值都为零，CovVel为协方差更新的系数，其一般取值在1～2之间。

式中，

3.2 航迹误差均值（RSS）

航迹误差均值RSS的计算公式如下所示：

3.3 航迹相关判决

在3.1、3.2的基础上，给出了航迹相关判决计算流程，如图2所示，其基本步骤如下：

步骤1：将综合航迹和观测航迹利用最小二乘法外推到当前仿真时间；

步骤2：计算两个航迹向量的差，得到一个差向量，进而进行差向量的模DeltaR；

步骤3：计算待关联航迹的误差均值MeasRSS和综合航迹的误差均值 Track RSS，令；

步骤4：按照下式计算待相关航迹与综合航迹的统计相关距离CorrDis。

其中，TotalMeasError=待相关航迹的位置误差+速度误差*外推时间，TotalTrackError综合航迹的位置误差+速度误差*外推时间。

4 关联冲突

在航迹关联过程，由于共有信息的不确定性、航迹分布密集等情况，可能发生关联冲突。所谓关联冲突指同一目标的航迹在不同周期关联上不同的综合航迹的情况。本文提出基于分段法解决关联冲突。

假设当前时刻为k时传感器1的第i条航迹和传感器2的第j条航迹关联成功，其系统航迹，在时间内传感器1的第i条航迹和传感器2的第j条航迹出现的次数分别为，两条航迹同时出现的次数为，经过第3节，该对航迹均能够关联成功，并赋予其系统航迹为，如果nk≠m，则当前时刻和历史关联之间存在冲突。采用分段法解决冲突，首选判定历史关联关系的次数是否大于1，如果，纠正k时刻的关联结果为nk=m，否则，表明历史关联结果中和当前时刻对应的结果只有一条，此时根据专属信息的唯一性，纠正当前时刻或历史关联结果。基本思想如下：

5 数值试验

将新算法应用于一个空中数据融合系统进行仿真。在目标分布密集的场景中，与经典最近邻域航迹关联算法（NNA）相比，新算法效果较好。

5.1 试验环境

假设数据融合系统包含3个可建立航迹的传感器（记为S、B和R），其中S的探测范围小，但扫描周期短（0.5 s），B探测范围大，数据精确，且探测数据具有专有信息，扫描周期较短（0.5 s）；R探测范围大，但扫描周期长（10 s），关联算法每2 s被驱动一次，系统基于VC6.0环境开发。

试验场景中目标分布情况如图3所示，该场景由6个空中平台构成，运行总时间为120 s，场景中11号平台负责对某海域进行监视支援，22号平台和81号平台互相监视，23号平台和82号平台互相监视。同时，12号平台在执行完侦察任务后返航。

由图3可知，相对于11号目标，22和81号方位差不超过1.5°，23和82号方位差不超过1°，距离差不超过1 km，4个目标构成了多目标的密集环境。

5.2 试验方法

由于传感器系统误差的存在，单次仿真结果的可靠性较差，因此，基于统计思想，将图3场景独立运行30次，并保存每次运行的航迹数据。最后，对30组数据进行统计计数，从而得出单次运行的关联成功率和总体成功率。

5.3 试验结论

经过统计计算后，多次运行后各个目标航迹关联率统计结果，如表1所示。

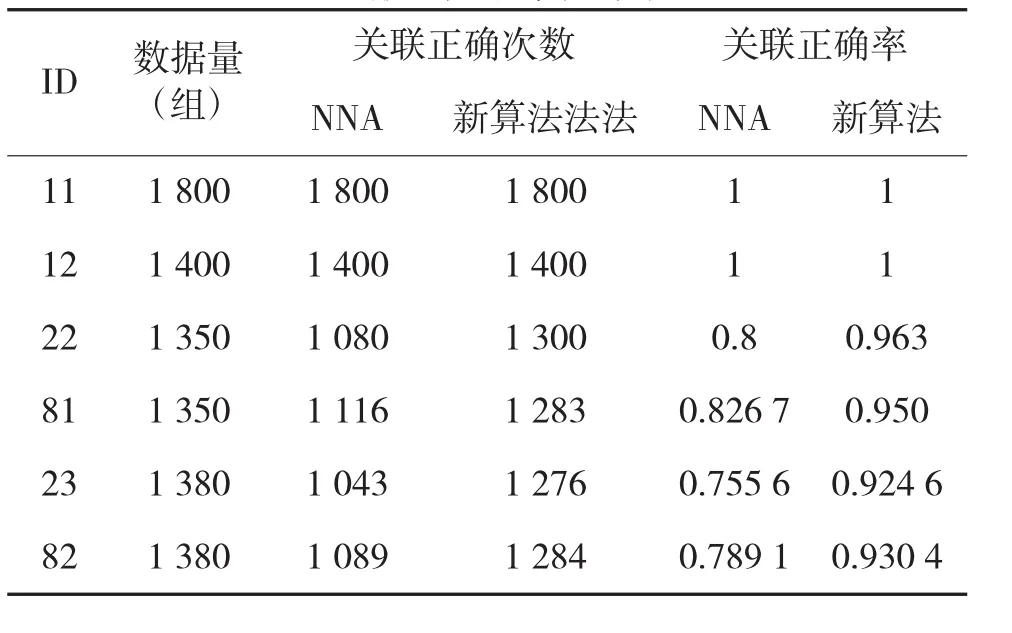
表1 航迹关联率统计结果

由表1可以看出，可以得出以下结论：

1）单个目标关联率：针对11号和12号离散目标，NNA和新算法的关联正确率均能达到100%；而针对22号和81号、23号和82两对密集目标，关联正确率均有大幅度提升。

2）总体关联率：NNA关联正确次数共有7 528次，而新算法关联正确次数共有8343次。新算法相对于NNA方法，整体关联率也有7 528/8 660=86.93%提升到了8 343/8 660=96.339%。因此，目标密集时，新算法能显著提高关联正确率。

6 结论

根据航迹的专属信息和共有信息的特点，提出了一种异类多传感器航迹关联的新算法。该方法通过完美关联，实现了专有信息的匹配，通过非完美关联，实现了共有信息的匹配，同时设计了航迹关联的流程和关联的计算方法。在此基础上，分析了关联冲突产生的原因，且提出冲突的解决办法。与传统最近邻域算法相比，该方法能够较好地解决航迹密集条件关联错误问题，计算方法相对简单，算法复杂度较低，便于工程实现。

［1］HALL D L，LLINAS J.Handbook of multisensor data fusion［M］.Washington:CRC Press，2001.

［2］SINGER R A，KANYUCK A J.Computer control of multiple site track correlation［J］.Automatica，1971，7（4）:455-463.

［3］BAR-SHALOM Y.On the track-to-track correlation problem［J］.IEEE Transactions on Automatic Control，2003，26（2）:571-572.

［4］BAR-SHALOM Y，CAMPO L.The effect of the common process noise on the two-sensor fused-track covariance［J］.IEEE Transactions on Aerospace&Electronic Systems，1986，AES-22（6）:803-805.

［5］KOSAKA M，MIYAMOTO S，IHARA H.A track correlation algorithm for multisensor integation［J］.Journal of Guidance Control&Dynamics，2015，10（2）:10-171.

［6］何友，谭庆海，蒋蓉蓉.多传感器综合系统设计中的航迹相关算法［J］.火力与指挥控制，1989，14（1）:1-12.

［7］BAR-SHALOM Y.On the sequential track correlation algorithminamultisensordatafusionsystem［J］.IEEETrans on Aerospace and Electronic Systems， 2008， 44（1）:396-396.

［8］BA N V，BA T V，PHUNG D.Labeled random finite sets and the bayes multi-target tracking filter［J］.IEEE Trans on Signal Processing，2014，62（24）:6554-6557.

［9］HANEBECK U D，BAUM M.Association-free direct filtering of multi-target random finite sets with set distance measures［C］//The 18th International Conference on Information Fusion.Washington:IEEE，2015:1367-1374.

［10］LIAN F，LIU J，HAN C.Error bound for joint detection and estimation of multiple targets with random finite set state and observation ［J］.IEEE Trans on Signal Processing，2015，117（12）:247-257.

［11］JONATHAN P B，MONICA F B，PETAR M D.RSSI-based multi-target tracking by cooperative agents using fusion of cross-target information ［J］.IEEE Trans on Signal Processing，2015，63（19）:5033-5044.

［12］吴卫华，江晶，冯讯，等.基于随机有限集得多目标跟踪算法概述［J］.电光与控制，2016，23（3）:1-6.

［13］杨威，付耀文.基于有限集统计学理论的目标跟踪技术研究综述［J］.电子学报，2012，40（7）:1440-1448.

［14］杨柏胜，姬红兵，高小东.随机集粒子滤波的快速被动数据关联算法［J］.西安电子科技大学学报，2010，37（4）：655-659.

［15］李军，黄力伟.基于统计加权的单传感器数据融合算法［J］.火力与指挥控制，2016，41（10）：184-187.

［16］吕鹏飞，彭冬亮，左燕，等.基于改进协方差控制的传感器管理算法［J］.火力与指挥控制，2016，41（7）:28-33.