基于有限元法的高频变压器漏电感和绕组损耗计算与分析
陈 彬, 李 琳, 刘海军, 陆振纲, 王志凯
(1. 新能源电力系统国家重点实验室, 华北电力大学, 北京 102206;2. 国家电网全球能源互联网研究院, 北京 102209)
1 引言
低频条件下,变压器的漏电感与交流电阻等参数可以用直流情况下的参数值代替。但是高频变压器的工作频率可达数十甚至数百kHz,其漏电感和交流电阻等参数受到高频涡流效应的影响,具有明显的频变特性[1,2]。在新型大功率智能DC-DC变换器中,高频变压器的漏电感作为谐振电路中的电感,以实现逆变/整流侧开关管的零电压开关(Zero Voltage Switching, ZVS),漏电感过大或过小都将造成变换器输出效率降低[3-6]。此外,随着工作频率、容量的提高以及变压器体积的减小,高频变压器的损耗和温升问题逐渐明显[7,8]。交叉换位技术(初次级的层或线匝交叠布置)可以削弱邻近效应,减小磁性元件内的漏磁场强度和交流电阻值,进而减小漏电感和绕组损耗[9-12]。
因此,在高频变压器的设计中,明确绕组结构和交叉换位方式对宽频区间内漏电感、交流电阻参数的影响规律,对于高频变压器的设计至关重要。本文利用ANSYS/Maxwell2D电磁场仿真软件,建立了对应于不同绕组布置方式的高频变压器二维有限元模型,采用有限元分析方法计算宽频区间内无交叉换位、部分交叉换位和完全交叉换位方式,以及不同绕组层数下漏电感和绕组损耗特性,明确了绕组结构和交叉换位布置方式对变压器漏电感和绕组损耗的影响。最后提出了高频变压器漏电感和绕组损耗的控制方法,该方法对于高频变压器的优化设计具有一定的指导意义。
2 基于有限元法的变压器参数计算原理
由于高频变压器具有三维旋转对称 (例如PQ型磁心)或轴对称(例如EE型和UU型磁心)的结构特点,因此可以将变压器简化为二维结构,在保证计算精度的前提下,以此降低建模难度和计算量。此时,所有电流量(包括源电流、涡流和位移电流)与所研究导体的横截面正交,例如导体截面在XY平面内,电流则为z轴方向。因此,与电流相关的矢量磁位A只有z轴方向。由于xy平面内无电流流过,电场强度E仅具有z轴分量,因此标量电位φ在导体截面上为常数。
在ANSYS/Maxwell2D电磁场仿真软件中,采用A-φ法来求解涡流问题,其场方程为:
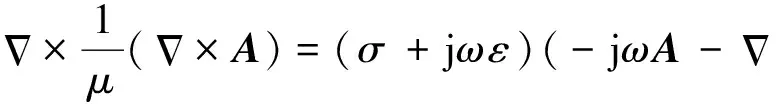
(1)
式中,A为矢量磁位;φ为标量电位;μ为相对磁导率;ω为激励的角频率;σ为电导率;ε为介电常数。
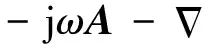
由于趋肤效应的影响,感应电流集中在导体的表面附近,超过趋肤深度,电流迅速衰减,随着频率的增加,趋肤深度减小。利用ANSYS/Maxwell2D电磁场仿真软件对高频变压器的绕组布置方式进行仿真分析时,考虑到导体区域存在趋肤效应的影响,因此选择涡流场求解器,对若干频点的漏磁场能量和绕组损耗进行扫频计算。导线区域存在趋肤效应,在趋肤效应层应进行加密剖分,趋肤效应层以下的网格可以相对稀疏,本文将透入深度的剖分层数设置为至少6层,其余区域采用自适应剖分。
利用短路测试条件下磁心窗口内绕组及其层间绝缘的漏磁场分布,通过漏磁场能量Wm与漏感Lσ之间的关系,进而计算出高频变压器的漏电感。对于由线性媒质组成的区域,各部分的漏磁场能量可表示为:
(2)
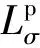
利用导体区域的涡流损耗计算交流电阻Rac,涡流损耗Pe的表达式为:
(3)
式中,Irms为绕组电流有效值。
3 高频变压器模型及试验验证
本文设计并制作了一台5kV·A/4.5kHz高频变压器模型,模型及其结构如图1所示。模型的主要参数如表1所示。模型磁心为芯式结构,磁心材料为非晶合金(CFCC630 Antainano®),叠片系数为0.82,非晶合金叠片厚度为25μm;磁心的最优工作磁密为0.178T。

图1 高频变压器模型Fig.1 High-frequency transformer model
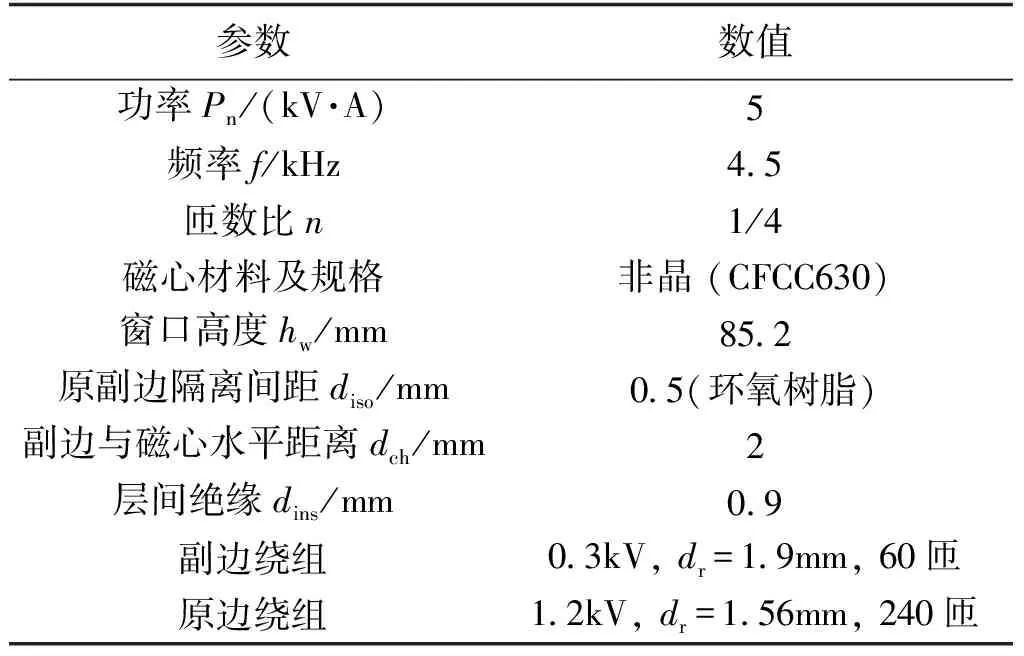
参数数值功率Pn/(kV·A)5频率f/kHz45匝数比n1/4磁心材料及规格非晶(CFCC630)窗口高度hw/mm852原副边隔离间距diso/mm05(环氧树脂)副边与磁心水平距离dch/mm2层间绝缘dins/mm09副边绕组03kV,dr=19mm,60匝原边绕组12kV,dr=156mm,240匝

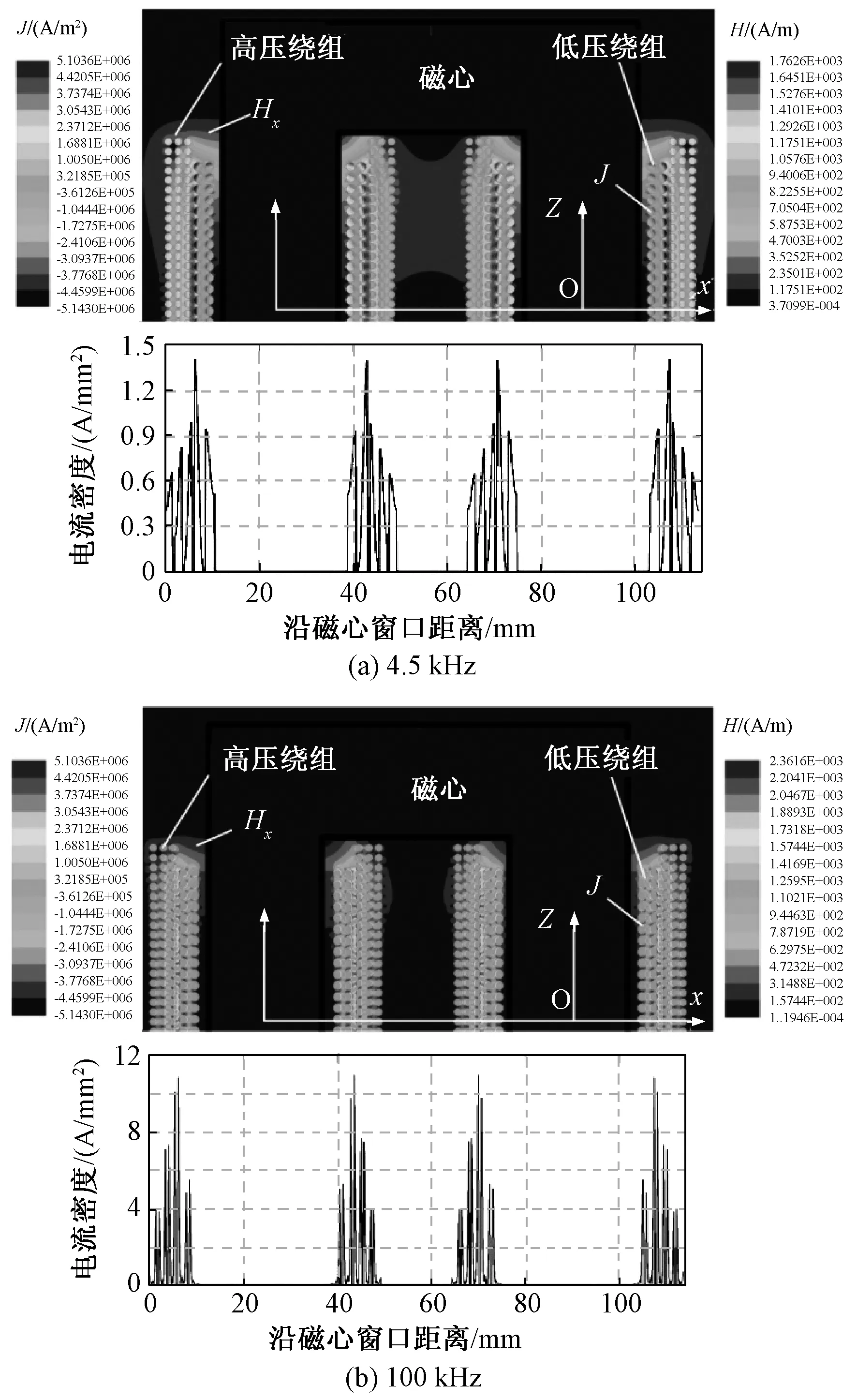
图2 漏磁场分布及沿绕组布置方向磁场强度Fig.2 Leakage magnetic field distribution and its strength along winding arrangement direction
采用Agilent 4294A高精度阻抗分析仪对高频变压器试验模型在40Hz~100kHz频率区间的漏电感和交流电阻进行测量。试验模型原边绕组与阻抗分析仪夹具电极相连,副边绕组短路,测量得到归算至原边侧的漏电感和交流电阻,结果如图3所示。
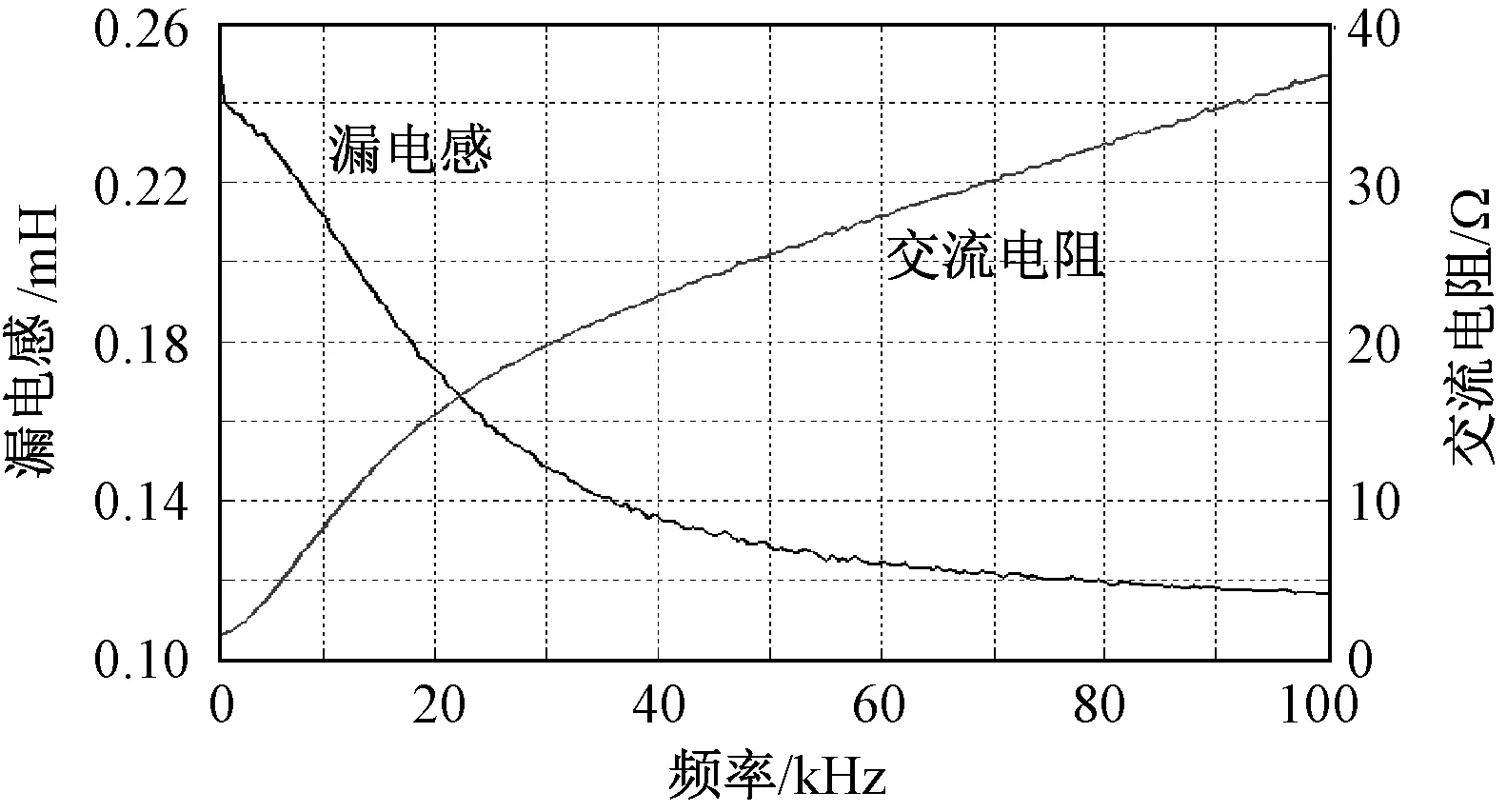
图3 漏感与交流电阻测量值Fig.3 Measurement values of leakage inductance and AC resistance
图4为有限元仿真法与实验测量方法获得的宽频区间内的漏电感和交流电阻系数。由图4可知,漏电感和交流电阻系数的仿真结果与测量结果变化趋势保持一致。由于二维有限元模型不能计及高频变压器磁心拐角处的绕组曲率效应,因此仿真结果与试验测量存在一定偏差。

图4 归算至原边侧的漏电感和原边绕组交流电阻系数Fig.4 Leakage inductance referred to primary side and AC resistance factor of primary winding
4 交叉换位方式对高频变压器参数的影响
4.1 原副边绕组交叉换位技术
交叉换位技术的优点是可以减小磁性元件磁心窗口内的最大漏磁场强度,使与漏磁场强度的平方成正比的漏磁能量降低,进而减小漏电感。这种效应在任何频率下,甚至是直流下都有效。同时,绕组交叉换位可以削弱邻近效应,降低由于邻近效应造成的绕组损耗。图5给出了4种绕组布置方式下的高频变压器。其中,图5(a)为无交叉换位式,即原边绕组的所有层形成一组,副边绕组的所有层形成另一组,两个绕组电流方向相反;图5(b)为部分交叉换位式,即绕组分别等分成M/2个区域(M为原边绕组或副边绕组层数),每个绕组区域包含两层原副边绕组,不同绕组区域交替布置,相邻绕组区域之间电流方向相反;图5(c)和图5(d)为完全交叉换位式,即原副边绕组各层交替布置。

图5 四种绕组布置方式Fig.5 Four winding configurations
图6为高频变压器在短路试验条件下电流密度J沿绕组布置方向的分布情况。由图6可知,在低频条件下(Δ=d/δ=0.5),高频变压器绕组的电流密度分布与绕组布置方式无关。但是,在高频条件下(Δ=d/δ=2),交叉换位技术对高频变压器绕组的电流密度分布存在明显影响,并且交叉换位程度越高,电流密度幅值越小。这是因为绕组交叉换位可以降低邻近效应,进而降低绕组的电流有效值。
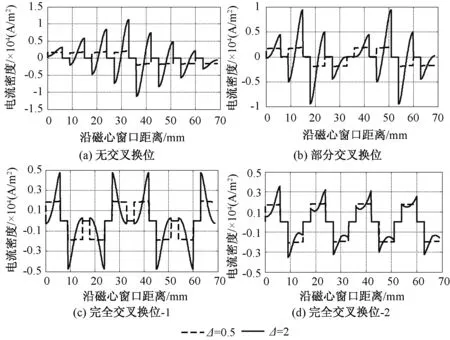
图6 导线中电流密度分布图Fig.6 Current density distribution in windings
图7为高频变压器在短路试验条件下漏磁场强度H沿绕组布置方向的分布情况。由图7可知,交叉换位技术对磁心窗口内漏磁场幅值产生明显影响。交叉换位程度越高,漏磁场强度幅值越小。与此同时,随着频率的增加,绕组导体区域的高频涡流效应逐渐增强,导体区域漏磁场强度呈现出与频率相关的复杂非线性分布,然而绝缘层内漏磁场强度始终呈线性分布。由于导体内漏磁场强度具有频变特性,该部分漏磁能量对应于绕组内部自感Lin,也会具有频变特性;绝缘层区域的漏磁场能量对应于绕组外部自感Lex,无频变特性。两部分之和组成总漏电感Lσ。因此,高频涡流效应将导致高频变压器的总漏电感具有频变效应。由此可知,高频变压器的漏电感和绕组损耗不仅取决于绕组布置方式、导线结构等几何因素,还会受到高频涡流效应的影响,具有一定的频变特性。

图7 磁心窗口内磁场强度分布Fig.7 Leakage magnetic field distribution in core window
4.2 高频变压器参数的仿真计算
为了明确绕组布置方式对高频变压器漏电感和交流电阻参数的影响,本文建立了对应于4种绕组布置方式的高频变压器二维有限元模型。磁心窗口高度为hw=100mm,原副边绕组直径均为d=6mm,原副边绕组为Mp=Ms=4层,每层匝数为Ntp=Nts=12,层间绝缘层厚度为dins=3mm,原副边绕组隔离间距diso=5mm。激励源选择电流,其峰值为Ip=Is=1A,原副边绕组导体的断面电流方向相反,选择实导体Solid属性,选择自适应求解。材料选择:磁心为Ferrite,绕组为Copper,绕组间的绝缘选择默认的vacuum。
图8(a)~图8(d)分别为短路试验条件下无交叉换位、部分交叉换位、完全交叉换位时原副边绕组及绝缘层内漏磁场和导体区域的电流密度仿真结果(Δ=2)。由于模型结构的对称性,因此仅给出模型上半部分。由图8可知,部分交叉换位后邻近效应削弱,绕组内部和绝缘层区域的最大漏磁场强度降低一半。完全交叉换位后邻近效应几乎全部消除,绕组内部和绝缘层区域的漏磁场强度为无交叉换位时漏磁场强度的1/4。完全交叉换位后,一方面漏磁场强度分布对于每一层绕组均相同,每一层就和单层绕组一样,绕组内部磁场强度降低,漏磁能量减小,进而使绕组内部自感Lin降低;另一方面,绝缘层内磁场强度降低,导致外部自感Lex相应减小。

图8 典型绕组布置方式下电流密度和漏磁场分布Fig.8 Current density and leakage field distribution of typical winding configurations
归算至原边侧的漏电感仿真值随归一化绕组厚度的变化曲线如图9(a)所示。由图9(a)可知,当归一化厚度由Δ=0.5上升至Δ=3.5时,无交叉换位、部分交叉换位、完全交叉换位-1、完全交叉换位-2四种绕组布置方式下,漏电感分别减小约38.17%、34.87%、48.43%、48.26%。当归一化厚度Δ>3.5时,总漏电感几乎保持恒定。这是由于当归一化厚度Δ较低时,导线内部漏磁场强度较大,导线内部存储一定的漏磁场能量。随着频率的增加,趋肤效应和邻近效应增强,导线内部的漏磁场强度和漏磁场能量降低,导致内部自感Lin减小,而绝缘层内部漏磁场强度和漏磁场能量保持不变,即导线外部自感Lex保持恒定。因此,在0.5<Δ<3.5区间内,总漏电感明显降低,具有明显的频变效应;当Δ>3.5以后,总漏电感几乎相等,不再具有频变特性。
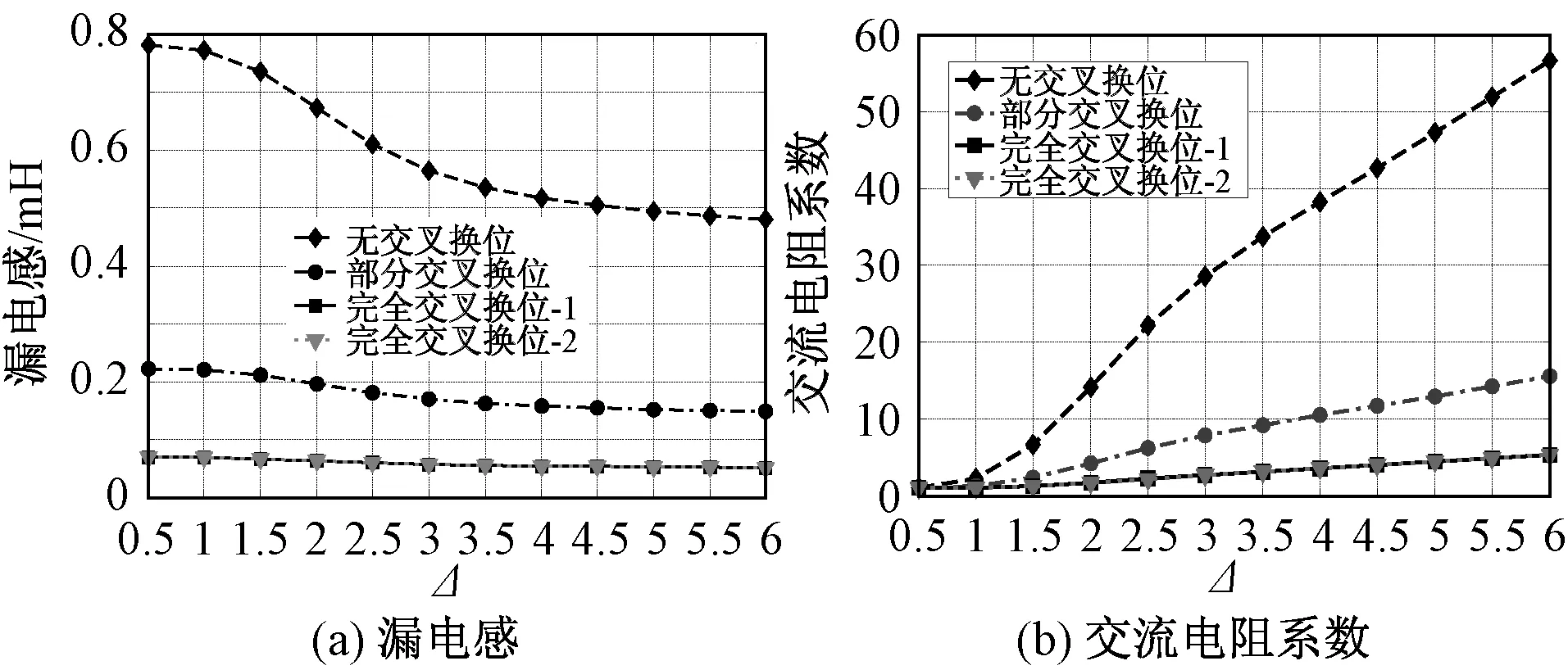
图9 不同绕组布置方式下漏电感交流电阻系数有限元仿真结果对比Fig.9 Leakage inductance and AC resistance factor under different winding configurations
采用有限元方法计算图8中不同高频变压器的高频涡流损耗Pe,根据计算式FRFEM=RFEM/Rdc(RFEM=2Pe/Ip2,Ip为原边绕组电流幅值),进而计算出交流电阻系数仿真值FRFEM。直流电阻Rdc=MlNt/(σπd2)=0.0293Ω。4种绕组布置方式下原边绕组交流电阻系数仿真值如图9(b)所示。由图9(b)可知,无交叉换位式对应的交流电阻系数最大,部分交叉换位式次之,完全交叉换位式最小。这说明交叉换位的程度越大,降低绕组损耗的效果越明显。但是,绕组完全交叉换位后会使原副边绕组间电容增大,影响变压器两侧的电压波形及功率输出效果[10]。
5 绕组层数对高频变压器参数的影响
保持原副边绕组的总匝数不变,控制单层绕组匝数,进而控制绕组层数,可以改变磁心窗口内的漏磁场强度分布情况。为了明确绕组匝数和层数对漏电感和交流电阻系数的影响规律,本文建立了对应于2种绕组结构的高频变压器二维有限元模型。磁心窗口高度均为hw=100mm,原副边绕组直径均为d=6mm,层间绝缘层厚度均为dins=3mm,原副边绕组隔离间距diso=5mm。激励源选择电流,其峰值为Ip=Is=1A,原副边绕组导体的断面电流方向相反,选择实导体Solid属性,选择自适应求解。材料选择:磁心为Ferrite,绕组为Copper,绕组间的绝缘选择默认的vacuum。两种情况下进行仿真:①原副边绕组为Mp=Ms=4层,每层匝数为Ntp=Nts=12;②原副边绕组为Mp=Ms=8层,每层匝数为Ntp=Nts=6。
在短路试验条件下原副边绕组间绝缘层内漏磁场和导体区域的电流密度仿真结果(Δ=2)如图10(a)和图10(b)所示。对比可知,随着绕组层数的增加,相邻层由邻近效应引起的涡流幅值和有效值也相应增加,所以多层绕组中邻近效应引起的绕组损耗增大,导致交流电阻系数增大。同时,随着绕组层数的增加,绝缘区域和隔离区域的漏磁场强度增大,造成高频变压器漏电感增加。
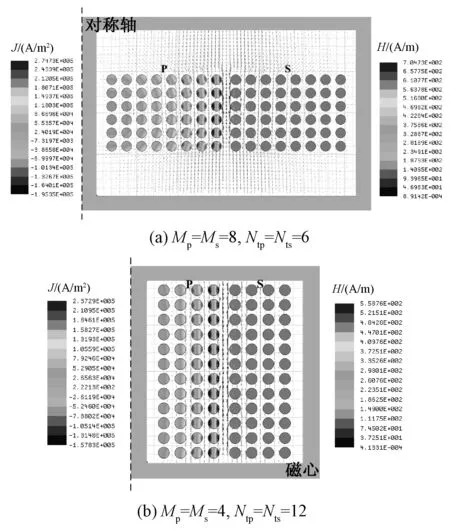
图10 电流密度和漏磁场强度分布Fig.10 Current density and leakage field distribution
图11为不同绕组层数时高频变压器漏电感和交流电阻系数在宽频区间内的变化情况(0.5<Δ<6)。由图11可知,随着绕组层数的增加,高频变压器漏电感和交流电阻系数明显增大。因此,在高频变压器设计过程中,确定原副边绕组匝数后,还要综合考虑绕组层数对漏电感和绕组损耗的影响。

图11 相同绕组匝数不同层数时漏电感和交流电阻系数有限元仿真结果对比Fig.11 Leakage inductance and AC resistance factor when Mp=Ms=4, Ntp=Nts=12 and Mp=Ms=8, Ntp=Nts=6
6 控制漏电感和绕组损耗的措施
(1)在原副边绕组的总匝数和原副边绕组的单层绕组匝数不变的情况下,改变原副边绕组的排布方式,可以改变磁心窗口内的漏磁场强度分布,进而改变高频变压器的漏电感和绕组损耗。采用部分交叉换位式绕组布置可以将磁心窗口内的漏磁场强度幅值降低一半,漏电感和交流电阻降低为无交叉换位方式时的1/4。采用完全交叉换位式绕组布置方式,漏电感和交流电阻降低为无交叉换位方式时的1/8。
(2)在原副边绕组的总匝数不变的情况下,控制单层绕组匝数,进而控制绕组层数,可以改变磁心窗口内的漏磁场强度分布。绕组层数减小时,高频变压器漏电感和交流电阻明显降低。
(3)通过控制绝缘纸的张数,控制原边绕组层间厚度、副边绕组层间厚度以及原副边绕组间隔离间距(单张绝缘纸厚度是固定的),这样可以改变储存于绝缘区域的漏磁能量,改变高频变压器的外部自感,从而改变高频变压器的总漏感。由于原副边绕组隔离区域的漏磁场强度最大,因此改变隔离间距的效果最为明显。如果忽略绕组端部效应的影响[13],可以认为高频变压器的绕组损耗不会随绝缘层和隔离间距的变化而改变。
7 结论
在高频变压器的优化设计中,为了控制漏电感和绕组损耗,需要改变绕组结构和布置方式。本文利用ANSYS/Maxwell电磁场仿真软件研究了宽频区间内漏电感和绕组损耗在不同绕组结构和排布方式下的变化规律,主要结论如下:
(1)在0.5<Δ<3.5区间,总漏电感明显降低,具有明显的频变效应;当Δ>3.5以后,总漏电感几乎相等,不再具有频变特性。
(2)绕组部分交叉换位可以使漏电感和交流电阻降低1/4,绕组完全交叉换位可以使漏电感和交流电阻降低1/8。
(3)控制绕组总匝数保持不变的情况下,降低绕组层数可以显著降低漏电感和绕组损耗。
[1] Shen Wei, Wang Fei, Boroyecich Dushan, et al. High-density nanocrystalline core transformer for high-power high-frequency resonant converter[J]. IEEE Transactions on Industry Applications, 2008, 44(1): 213-222.
[2] 陈彬,李琳,赵志斌(Chen Bin, Li Lin, Zhao Zhibin).一种考虑频变特性的大容量高频变压器漏电感解析计算方法(An analytical calculation method of leakage inductance in high-power high-frequency transformers considering frequency dependence characteristic)[J].中国电机工程学报(Proceedings of the CSEE),2017,37(13):3928-3937.
[3] 李子欣,高范强,徐飞,等(Li Zixin, Gao Fanqiang, Xu Fei, et al.).中压配电网用10kVac-750Vdc/1MVA电力电子变压器功率密度影响因素研究(Power density analysis of 10kVac-750Vdc/1MVA power electronic transformer/solid-state transformer for medium voltage distribution grid)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy),2016, 35(4):1-6.
[4] Oggier G G, Garcia G O, Oliva A R. Modulation strategy to operate the dual active bridge DC-DC converter under soft switching in the whole operating range[J]. IEEE Transactions of Power Electronics, 2011, 26(4): 1228-1236.
[5] Naayagi R T, Andrew J Forsyth, Shuttleworth R. High-power bidirectional DC-DC converter for aerospace applications[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4366-4379.
[6] 赵志英,秦海鸿,龚春英,等(Zhao Zhiying, Qin Haihong, Gong Chunying, et al.).变压器分布电容对高频变压器反激变换器的影响及其抑制措施(Influences and suppression method of transformer winding capacitance in high-frequency high-voltage flyback converter)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy),2006,25(4):67-75.
[7] Villar I, Rufer A, Viscarret U, et al. Analysis of empirical core loss evaluation methods for non-sinusoidally fed medium frequency power transformers[A]. IEEE International Symposium on Industrial Electronics, ISIE[C]. 2008. 208-213.
[8] 张宁,李琳(Zhang Ning, Li Lin).基于ANSYS仿真的绕组交叉换位对高频变压器损耗的影响分析(Analysis of effect of interleaving technique on winding loss of high-frequency transformer based on ANSYS simulation) [J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy),2015,34(10):76-80.
[9] 李智华,罗恒廉,张青春,等(Li Zhihua, Luo Henglian, Zhang Qingchun, et al.).绕组交叉换位对高频变压器参数影响分析(Synthetically analysis of effect of interleaving techniques on high-frequency transformer parameter)[J].高电压技术(High Voltage Engineering),2008,34(11):2453-2458.
[10] Barrios E, Urtasun A, Ursua A. High-frequency power transformers with foil windings: Maximum interleaving and optimal design[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5712-5723.
[11] Pavlovsky M, de Haan S W H, Ferreira J A. Partial interleaving: A method to reduce high frequency losses and to tune the leakage inductance in high current, high frequency transformer foil windings[A]. IEEE 36th Power Electronics Specialists Conference, PESC[C]. 2005. 1540-1547.
[12] 赵争涵,汪友华,凌跃胜,等(Zhao Zhenghan, Wang Youhua, Ling Yuesheng, et al.).大容量高频变压器绕组损耗的计算与分析(Calculation and analysis of loss in high-capacity high-frequency transformers)[J].电工技术学报(Transactions of China Electrotechnical Society),2014,29(5):261-270.
[13] Dimitrakakis G S,Tatakis E C. High-frequency copper losses in magnetic components with layered windings[J]. IEEE Transactions on Magnetics, 2009, 45(8): 3187-3199.

