多腹板箱梁不均匀受力特性分析

林志滔

(福州市规划设计研究院 福建福州 350108)

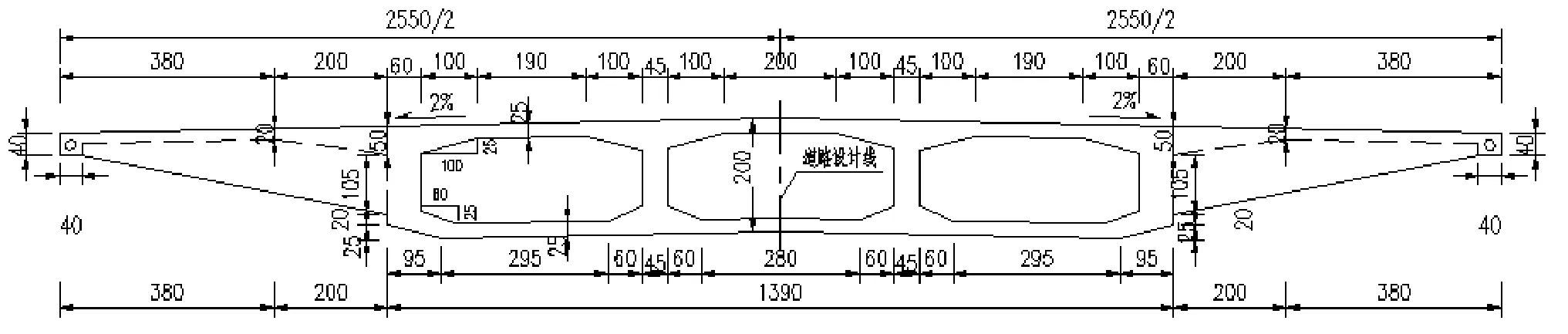
图1 箱梁断面图

2 建立模型

为验证结构安全性及可靠性，本文采用有限元程序MIDAS FEA建立全桥空间有限元计算模型，对结构进行验算，分析大挑臂箱梁多腹板之间不均匀受力特性。在该模型中，箱梁的顶板、底板、腹板、横梁、齿块及横肋均采用六面体实体单元，其8个节点各有6个自由度，即3个线位移和3个角位移，预应力钢束采用钢筋单元模拟。

在以往的预应力混凝土结构分析中，预应力钢束多以等效荷载方式进行模拟，其概念清晰但并不适用于较复杂的配索形式。而在MIDAS FEA中，可采用钢筋模块来模拟预应力钢束，利用钢筋单元+母单元(嵌入式钢筋)这种组合考虑摩擦损失、钢筋回缩损失、弹性变形损失、收缩和徐变损失等预应力损失，耦合相对位移，提高计算精度。

全桥3m×37m计算模型如图2所示，共43 786个节点，混凝土单元共140 868个，钢筋单元1133个。

2.1 荷载工况

多腹板不均匀受力问题，主要是由横向刚度分配、支座间距以及偏心活载布置引起，因此，采用实体模型单元分析自重、二恒、汽车偏心荷载。一期荷载结构自重程序自动考虑，二期恒载(包含防撞护栏、铺装等)按实际位置加载，汽车荷载(偏心)按车道面布置施加于顶板上，由程序自动按最不利影响线进行纵向加载。同时，计算工况分别按照汽车偏载(中腹板)工况以及汽车偏载(边腹板)工况考虑。具体荷载布置如图3所示(一期恒载容重：r=26.5kN/m3，二期恒载重，二期恒载合计119.8kN/m)。

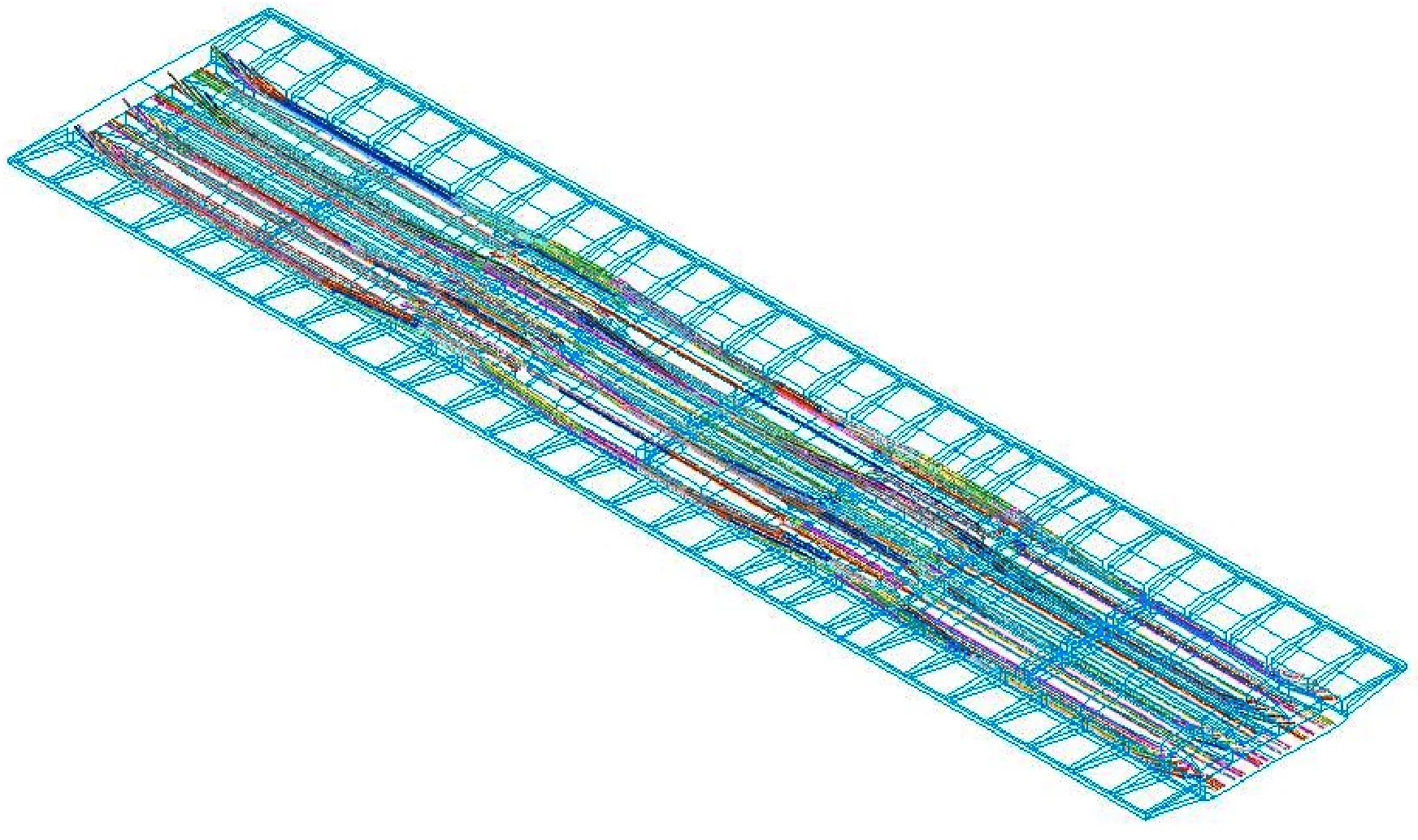
图2 有限元模型示意图

汽车偏载(中腹板)工况按三车道汽车轴重布置于接近中腹板位置，汽车偏载(边腹板)工况按三车道汽车轴重布置于外悬臂位置。

3 计算结果

3.1 纵向结果比较

单梁模型采用midas civil建立空间有限元模型进行纵向计算，并与实体空间有限元模型计算结果进行比较，验证计算模型精确度。

单梁模型共51个空间梁单元，52个节点，如图4～图8所示。

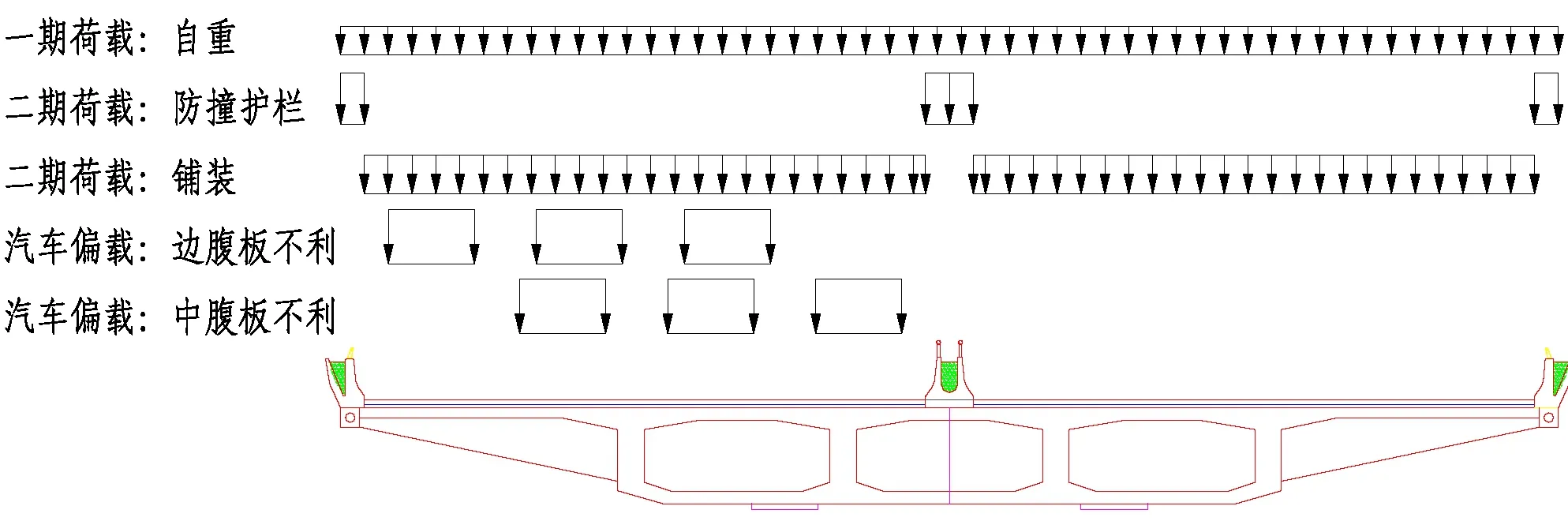
图3 加载工况图

图4 单梁模型

图5 单梁模型——顶板正应力(MPa)

图6 实体有限元模型——顶板正应力(MPa)

图7 单梁模型——底板正应力(MPa)

图8 实体模型——底板正应力(MPa)

针对单梁模型与实体模型，进行标准组合作用(自重+二期+预应力+活载+温度+沉降)下顶底板应力比较。由上述计算结果可知，单梁模型与实体有限元模型，在纵向整体计算时得到平均意义上顶底板应力较为吻合，如表1所示。但大悬臂小间距箱梁桥不同腹板位置顶底板应力以及腹板受力有一定差异。由于单梁模型的局限性，计算时不能精确模拟横向刚度，无法提取大悬臂下腹板内力不均匀分布数据，因此，现阶段大挑臂多箱室箱梁单梁模型均以偏载系数的经验值来判断各个腹板受力不均匀性，存在一定的局限性。

表1 单梁模型与实体模型(恒+活)标准组合下顶底板平均应力比较 MPa

3.2 腹板剪力计算

实体模型中，中边腹板内力均按有限元分析结果得出各个有限元单元的正应力与剪应力，为方便进行中边腹板的剪力值比较，将实体模型中各单元腹板剪应力换算成腹板剪力[1]。由于截面全部剪应力的总合力等于竖向剪力，因此可根据每条腹板的剪应力分布数值进行直接积分，精确计算每条腹板的竖向剪力。对于一般截面的剪力流可对每个有限元单元的剪应力进行积分累加得到总的剪力Vy为

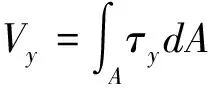
根据式(1)计算各个工况如自重、二期、汽车偏载(边腹板)和汽车偏载(中腹板)下各条腹板的剪力以及总剪力。

3.3 不同加载工况下腹板剪力分配(支座间距6m)

支座间距为6m工况下，选取3个有代表性的截面位置进行腹板剪力计算比较，分别为中支点(边跨侧)，中支点(中跨侧)和边支点截面处，剪力值如表2～表4所示。

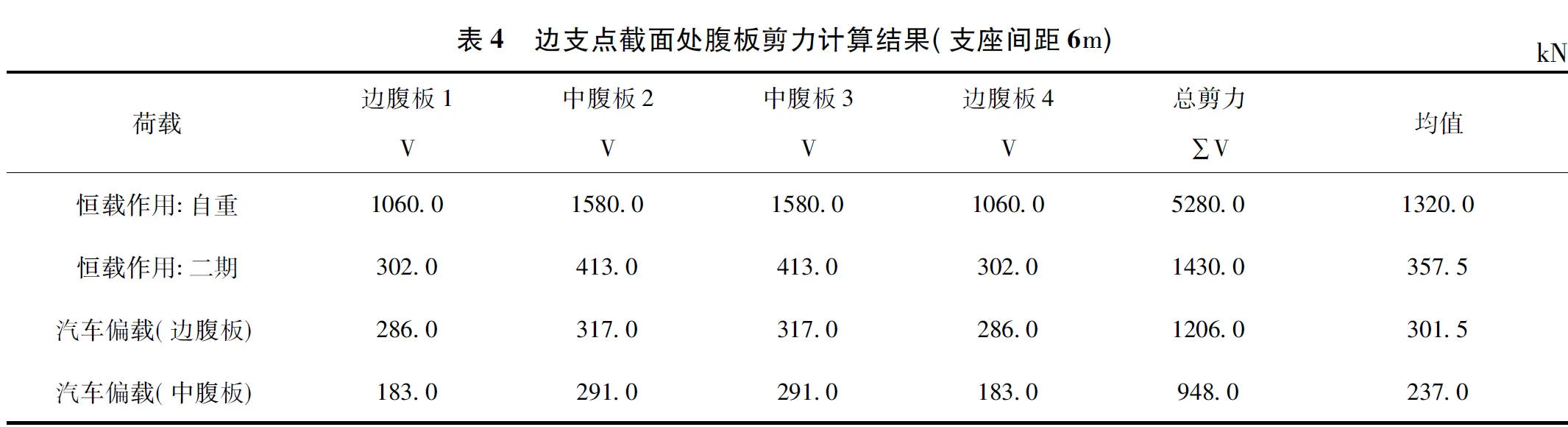
桥面宽度为25. 5m、支座间距为6m 时，两侧边腹板恒载剪力值较小，在恒载作用下中腹板受力明显大于边腹板。不论是汽车荷载轴重作用于边腹板还是中腹板，中腹板剪力均大于边腹板。当加载于边腹板时，腹板受力不均匀性更为明显，且中支点位置的剪力不均匀性较边支点明显。

3.4 不同加载工况下腹板剪力分配( 支座间距9m)

为比较不同支座间距下腹板剪力分配的变化规律，将支座间距拉大到9m，并同样选取与上工况相同的截面位置进行腹板剪力计算比较，剪力值如表5 ～表7 所示。

在该工况中将箱梁支座间距拉开到9m,3 个截面的剪力分布均呈现相同的变化趋势。在恒载作用下，边腹板的剪力值较上一工况增大明显，中腹板剪力值减小，恒载的剪力分布趋于平均。在活载偏载作用下，边腹板与中腹板的剪力增长幅度均小于上一个工况。

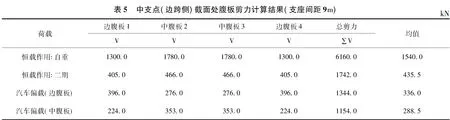
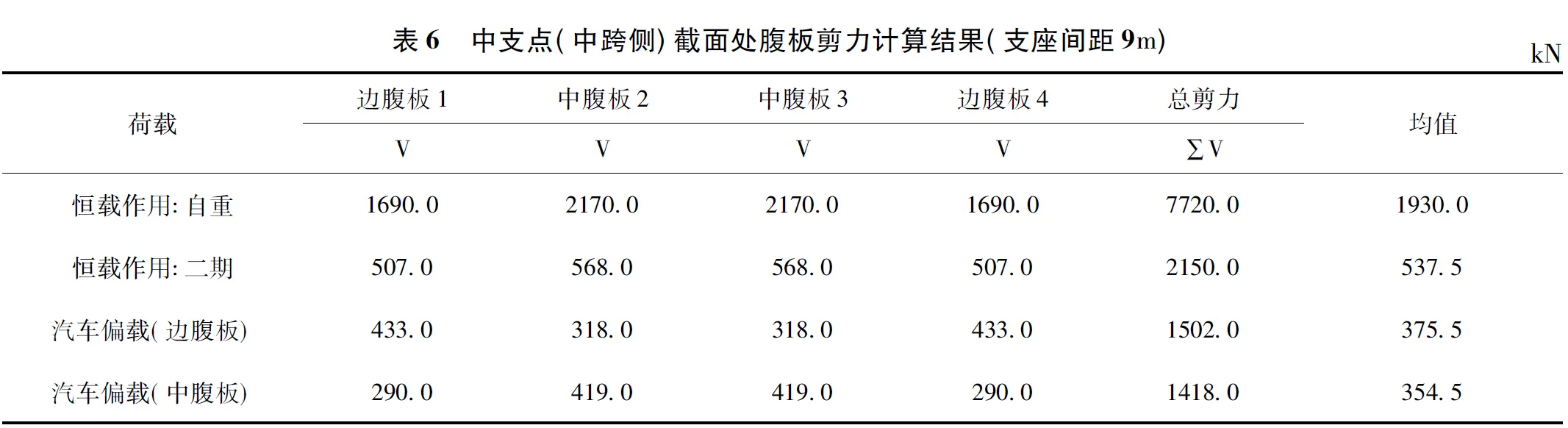
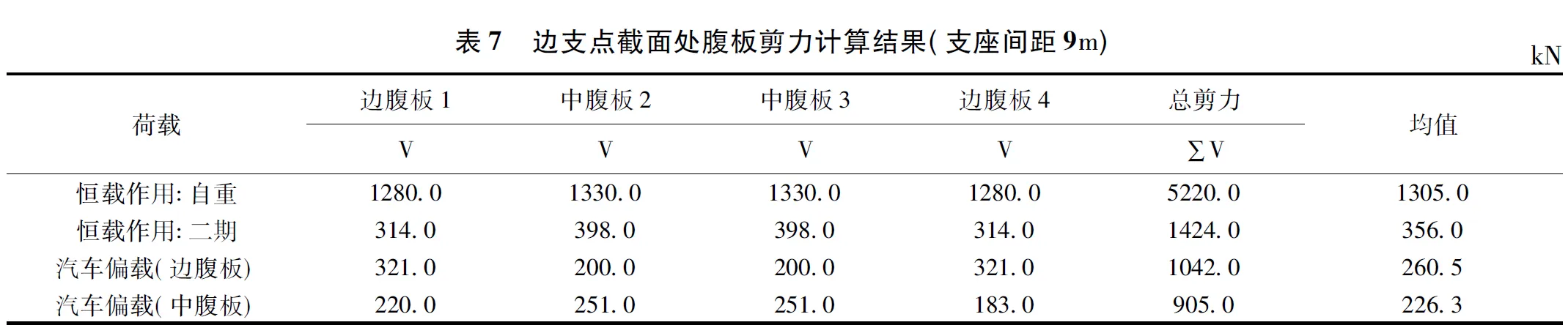
表8中支点位置(中跨侧)截面腹板剪力在不同支座间距下最大偏载系数

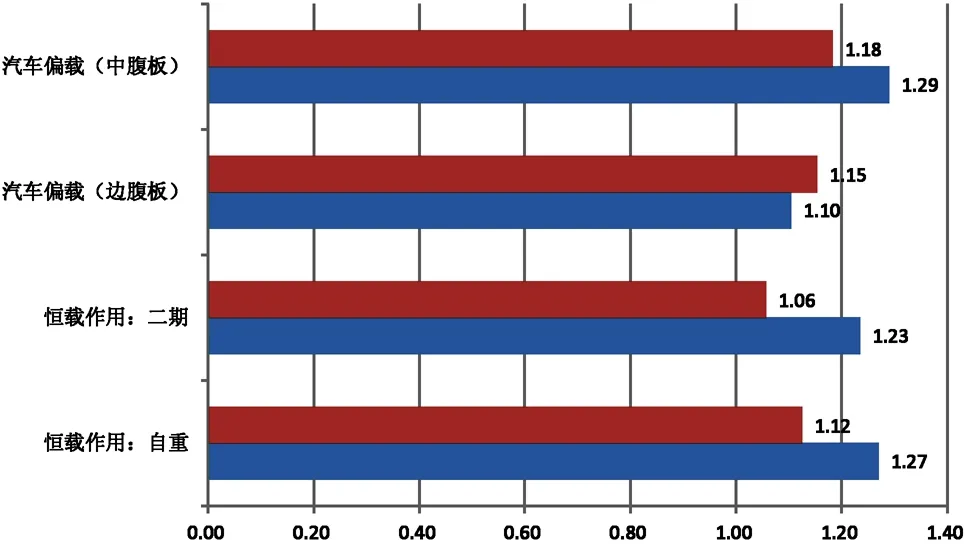
表9 中支点位置(边跨侧)截面腹板剪力在不同支座间距下最大偏载系数

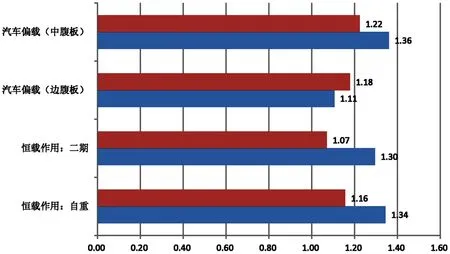
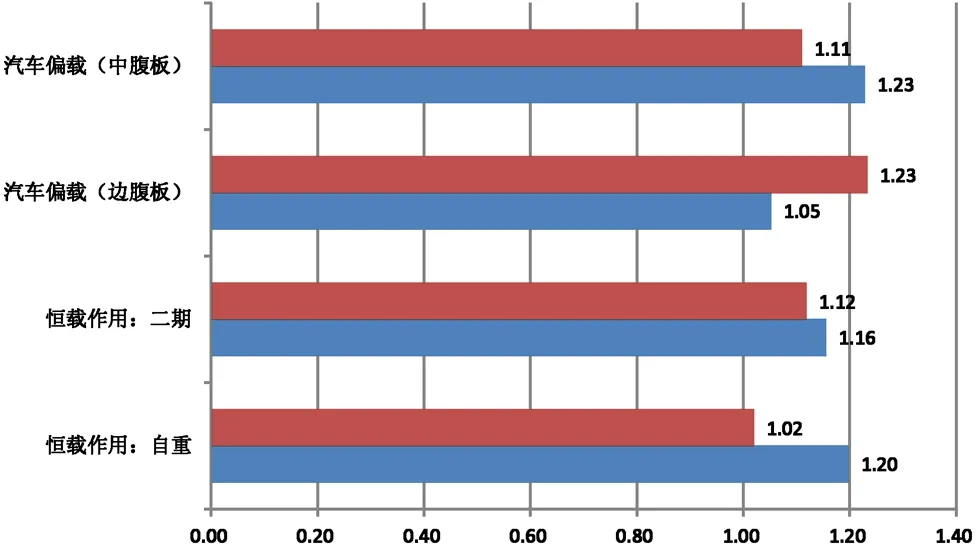
表10 边支点位置截面腹板剪力在不同支座间距下最大偏载系数

3.5 结果分析

如表8～表10所示，在桥面宽度为25.5m，支座间距为6m时，恒载剪力偏载系数为1.16～1.34，在恒载作用下中腹板受力明显大于边腹板；汽车荷载中腹板剪力偏载系数为1.23～1.36，边腹板剪力偏载系数为1.05～1.11，中腹板腹板分布的不均匀性较边腹板明显。

在桥面宽度为25.5m，支座间距为9m时，恒载剪力偏载系数为1.02～1.16，在恒载作用下中腹板受力大于边腹板。汽车荷载中腹板剪力偏载系数为1.11～1.22，边腹板剪力偏载系数为1.15～1.23，中腹板与边腹板受力不均匀性较为接近。

通过上述比较可知，在支座间距小时，恒载、活载作用下中腹板受力不均匀性较为明显。在支座间距大时，恒载、活载作用下中腹板、边腹板受力趋于均衡。

4 结语

大挑臂箱梁具有桥下空间利用率高，满足桥下城市道路或辅道布置、节约用地等优点[3]，因此，在城市中广泛应用。本文以福州市南台大道南段道路工程中大挑臂多腹板连续箱梁桥为例，利用MIDAS FEA建立全桥空间有限元计算模型，分析不同支座间距下腹板不均匀受力特性，从文中分析可得出以下结论：

(1)在支撑比大于4的连续箱梁横向分析中，以恒载(扣除横梁自重)及附加力支反力以集中力形式施加于腹板中心线计算，边腹板应考虑1.35恒载偏载系数。活载支反力以集中力形式施加于腹板中心线，边腹板可考虑1.1偏载系数，中腹板考虑1.35偏载系数，再进行包络验算。

(2)支座间距对恒载及活载的剪力分配影响较大，支座间距越小，大挑臂多腹板箱梁在恒载、活载作用下受力呈现越明显的不均匀性，且中腹板的受力越大，边腹板受力越小。

[1] 郑振，谷音.大悬臂变截面箱梁剪力滞效应分析[J].福州大学学报,2001,29(2):62-65.

[2] 华波，朱朝阳，朱安静.大悬臂多腹板宽箱梁受力特性研究[J].交通科技，2012(2)：1-3.

[3] 王伟臣.展翅梁桥上部结构设计简介[J].公路，1999(10)：12-15.