含软弱夹层围岩计算模型分析及危险度评估
李之达 张 泾 冯 旺
(武汉理工大学交通学院1) 武汉 430063) (中国市政工程中南设计研究总院有限公司2) 武汉 430019)
0 引 言
软弱夹层是岩层中的不连续结构面形成的具有一定厚度的夹层,夹层中的填充物通常有破碎岩块、夹泥、碎土、砂岩等,其变形模量和强度均低于周围岩均质层.软弱夹层是围岩的薄弱部位,在这些部位处,围岩变形不连续,且由于较低的弹性模量导致较大的变形,应力分布相对于均质围岩也不同;夹层处强度较低,围岩的破坏往往从软弱夹层部位开始.对于含软弱夹层围岩的研究,由于物质和变形的不连续,往往呈现出非线性的性质,因此,理论上求解十分困难,目前主要通过一些简化的物理模型来模拟其性质.周辉等[1]通过对屈服准则的研究,建立了屈服接近度函数,以此来描述围岩危险程度,与单纯用单轴应力强度理论来判别围岩稳定性的方法相比根据有优越性,同时可以对非塑性区的围岩的危险程度进行判定,对于研究围岩渐进破坏演化特性具有重要意义.吴旭平等[2]结合工程实际,不研究具体软弱夹层的位置的影响,只在该工程实践中研究含软弱夹层围岩的收敛变形,地表沉降和塑性区发展等性质;黄锋等[3]通过数值模拟,提出了基于损伤本构模型,研究并划分了围岩松动区、拱压区、破坏区的范围分布;Jeon等[4]通过相似模型试验研究了断层和软弱结构面对隧道围岩稳定性的影响;Fei等[5]采用了一种温度感应材料来模拟软弱夹层的性质,并研究了大型水工结构的稳定性.石少帅等[6]通过数值模拟,分析了软弱夹层位置和倾角对于围岩变形、塑性区分布、应力分布的影响;郭富利等[7]将夹层简化为受轴向力和横向力的梁的物理模型,分析了夹层的破坏过程,并研究了夹层破坏导致围岩破坏的演化过程;张志强等[8]研究了夹层厚度对围岩的影响,并提出了用接触单元来模拟不连续的位移和强度,用影响带单元和等效变形模量来模拟连续大变形的方法来模拟软弱夹层的性质.郑颖人等[9]利用弱化材料参数的等效连续体对厚度较大的软弱夹层进行模拟,并研究了含软弱夹层围岩开挖稳定性的问题.
本文从两方面进行分析:①对软弱夹层围岩边界进行简化,提出计算软弱夹层边界应力的物理模型,并推导相应的求解方程;②再根据均质围岩的破坏特征,利用应力张量和屈服准则推导围岩在复杂应力状态下的ξ系数.结合工程实例,通过数值计算软件FLAC3D对上述理论进行验证,分析含软弱夹层围岩ξ系数的分布特征.
1 含软弱夹层围岩计算模型分析
对于软弱夹层的受力情况进行分析,考虑软弱夹层对于夹层附近的围岩受力变形影响较大,而对远离夹层的围岩影响较小,可取一定夹层影响范围内均质围岩与软弱夹层共同构成的组合结构.考虑夹层位置分布属于贯穿洞室的这种最不利的情况进行分析,可建立如图1的矩形组合梁结构物理模型,利用组合梁结构理论计算.其左边自由端为洞室临空面,将该范围内洞室边界简化为直线,右端为固定端.为简化分析,现作如下假定:①各层岩体简化为梁,组成组合梁结构,均质围岩边界的受力情况与无软弱夹层时围岩的受力情况相同;②对于梁结构,不考虑由于梁上下表面首竖向荷载挤压所产生的高度方向的挤压变形,其挠度仅受梁弯矩影响;③各层均处于在弹性状态下,夹层与均质岩体始终法向接触.

图1 计算模型简图
图中:q1(x),q4(x),τ1(x),τ4(x)均已知,q2(x),q3(x),τ2(x),τ3(x)为待求.根据平衡条件,可得
(1)
由于各层始终法向接触面,可认为各层梁曲率相同,即
Φ1(x)=Φ2(x)=Φ3(x)=
(2)
联立式(1)~(2)并对等式两边求2阶导数,可得
(3)
对于各层接触面的纵向应变,根据材料力学可得
(4)
由于未发生滑移,所以有
(5)
联立式(4)~(5)并对等式两边求2阶导数可得
(6)
(7)
(8)
联立可求τ2(x)、τ3(x),具体问题可代入数值用计算机求解.
若接触面之间产生滑移,假设为粘结摩擦滑移,滑移段长度为l,则利用接触面粘聚抗剪公式
τmax(x)=c0+μ0q0(x)
(9)
使接触面的剪力服从该表达式.其中:c0为接触面粘聚力;μ0为摩擦系数;q0(x)为接触面法向压力.联立式(3)、式(9),且对各等式两边求2阶导数可得
(10)
代入参数a,b化简后可得一阶线性微分方程组
(11)

为已知函数向量.
利用一阶线性微分方程组通解公式

(12)
求得含有参数c1,c2的通解(可设t0=0).再把q2(x),q3(x)代入式(8)联立求解,即可求出c1,c2,其求解过程较为复杂,可用数值计算软件进行.再利用式(9)可求l区段内的剪力分布,对于滑移段以外的应力分布情况,由于篇幅限制,不再讨论.求出软弱夹层边界力后,可根据材料力学理论对其内力进行求解,分析其受力破坏情况.
2 围岩屈服分析
根据Mohr-Coulomb准则,为表示围岩的危险程度,考虑围岩在平面复杂应力状态下屈服破坏,引入屈服接近度的概念.由于围岩大多是受剪破坏,暂不考虑拉应力下的屈服.将围岩的某一点的应力张量分解为应力球张量σm和应力偏张量sij,令σ1>σ2,可得应力球张量和应力偏张量第二不变量表达式为
(13)
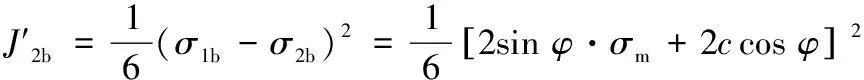

(15)
式中:ξ为屈服接近度,在莫尔应力圆上对应为该点应力圆的半径与保持圆心不变达到屈服时的应力圆半径之比.同时可推出在x-y坐标系下
(16)
所以不论围岩是否处于何种应力状态,均可由ξ系数判断围岩的危险程度.当ξ=1时围岩屈服,ξ<1时围岩处于弹性状态,且ξ越大表明围岩越接近屈服.
3 数值模拟分析
选取马家河隧道在K0+734附近的区域围岩为例,通过数值模拟对其围岩稳定性进行计算分析.该地段围岩等级为III级,该地段为风化钠长石英片岩,节理裂隙发育,且存在一条1 m宽与水平面成45°的经过洞室中心的破碎夹层贯穿隧洞,石英、云母含量高,节理裂隙发育,易掉块,地下水较发育,呈滴水状.隧道洞室净宽10.4 m,净高8.2 m,该地段隧道隧道埋深为160 m.选取宽为80 m、高为100 m的矩形区域为研究区域,左右边界固定水平位移,底部边界固定水平和竖向位移,顶部边界自由,所有区域固定平面外位移,初始地应力场为围岩自重应力场施加,先进行自重初次平衡后再一次性开挖求解,屈服时物理模型采用Mohr-Coulomb准则,数值计算软件采用FLAC3D 5.0,软弱夹层与均质围岩接触界面采用软件内置的interface单元.其物理力学参数见表1.

表1 围岩计算物理力学参数
3.1 计算模型分析验证

(17)


图2 软件计算值与理论值对比

3.2 数值模拟围岩ξ系数分布
采用表1的计算参数以及Mohr-Coulomb准则进行计算,根据式(16)设置extra变量可获得隧道围岩的ξ系数云图,由于均质围岩与软弱夹层的物理参数不同,其ξ系数的计算参数不相同,因此将各自的ξ系数云图分开表示再图层叠加,见图3.

图3 隧道围岩ξ系数云图
由图3可知,均质围岩大部分区域的ξ系数均在0.5以下,而软弱夹层区域的ξ系数最小为0.69,因此相对于均质围岩,软弱夹层更容易达到屈服.ξ系数较高的区域集中在洞室周边左右两侧和软弱夹层及其周围的区域,需要重点关注.然后输出围岩的塑性区云图,见图4.

图4 隧道围岩塑性区云图
由图3~4可知,考虑到计算机运算的精度问题,可将ξ>0.98的区域定义为围岩的一级危险区,该区域分布接近于围岩塑性区的分布,其危险程度最高,见图5a).再将0.9<ξ<0.98的区域定义为围岩的二级危险区,见图5b).该区域的围岩虽然未达到屈服,但ξ较大,具有一定的风险,也需要注意.在软弱夹层中的二级危险区的大部分区域距离洞室较远,即便屈服对于隧道的安全性也影响很小,因此需要结合危险点的位置综合评估.综上,对于一级和二级危险区,尤其是洞室周边区域,在设计或者施工时需要重点关注.

图5 围岩危险区ξ系数云图

图6 围岩一级危险区位移云图

图7 围岩二级危险区位移云图
对一、二级危险区域的位移情况进行分析,提取对应区域的水平位移绝对值与竖向位移绝对值的云图,见图6~7.对于第一危险区,其水平位移绝对值分布在0~4.65 mm,竖向位移绝对值分布在0~7.34 mm,离洞室较远的夹层部位由于受到两边围岩的约束位移较小,而在洞室周边尤其是软弱夹层部位附近,位移较大.对于第二危险区,其水平位移绝对值分布在0~1.85 mm,竖向位移绝对值分布在0~9.28 mm,其位移极值超过第一危险区的位移极值.上述表明在位移较小的区域,其围岩的ξ系数也可能较高,即危险程度较高.
综上所述,通过围岩的ξ系数,并结合危险点所在的位置,能够较好的反应不同部位隧道围岩的危险程度,尤其对于含软弱夹层的围岩隧道,能够更好的发现其薄弱部位,从而及早的采取相应措施,保证隧道围岩的安全.
4 结 论
1) 将含软弱夹层围岩简化为组合梁结构模型具有一定的可行性,适当简化后,可以从理论上计算软弱夹层的应力分布,其正应力的相对误差在两端边界处较大,离开一定距离后较小.
2) 根据应力张量和Mohr-Coulomb屈服准则推导出的ξ系数能够更好的反应围岩在复杂应力状态下的危险程度,用过对危险等级分区,可以作为找出围岩的薄弱部位,以便更好的采取相应措施对其进行处理,保证隧道结构的安全,为设计,施工提供理论依据.
3)ξ系数较高的区域集中分布在洞室边界和软弱夹层部位,且软弱夹层部位的ξ系数明显高于均质围岩部位,其对于某些位置其计算的位移量很小,但ξ系数值可能很高.对于距离洞室边界很远的位置,虽然ξ系数的值较高,但如果屈服对围岩整体影响不大时,也可以不考虑.因此,危险程度的判定应该结合ξ系数与危险点所在的位置综合评定.
[1] 周辉,张传庆,冯夏庭,等.隧道及地下工程围岩的屈服接近度分析[J].岩石力学与工程学报,2005(17):3083-3087.
[2] 吴旭平,杨新安,李亚翠,等.含软弱夹层浅埋隧道变形特性及控制指标研究[J].岩石力学与工程学报,2014(增刊1):2685-2691.
[3] 黄锋,朱合华,徐前卫.含软弱夹层隧道围岩松动破坏模型试验与分析[J].岩石力学与工程学报,2016(S1):2915-2924.
[4] JEON S, KIM J, SEO Y, et al. Effect of a fault and weak plane on the stability of a tunnel in rock—a scaled model test and numerical analysis[J]. International Journal of Rock Mechanics and Mining Sciences,2004,41:658-663.
[5] FEI W, ZHANG R, ZHANG L. Experimental study on a geo-mechanical model of a high arch dam[J]. International Journal of Rock Mechanics and Mining Sciences,2010,47(2):299-306.
[6] 石少帅,李术才,李利平,等.软弱夹层对隧道围岩稳定性影响规律研究[J].地下空间与工程学报,2013(4):836-842.
[7] 郭富利,张顶立,苏洁,等.含软弱夹层层状隧道围岩变形机理研究[J].岩土力学,2008(1):55-58.
[8] 张志强,李宁,陈方方,等.软弱夹层厚度模拟实用方法及其应用[J].岩石力学与工程学报,2010(1):66-71.
[9] 郑颖人,王永甫,王成,等.节理岩体隧道的稳定分析与破坏规律探讨:隧道稳定性分析讲座之一[J].地下空间与工程学报,2011(4):649-656.

