箱梁合龙束径向力的横向效应分析与防治措施

向木生 石 彬 严琼建

(武汉理工大学交通学院1) 武汉 430063) (湖北交投智能检测股份有限公司2) 武汉 430050)

0 引 言

预应力混凝土连续箱梁桥有较大的跨度能力、良好的整体性和承载能力、外观简洁等优点，在越来越多的新建桥梁中得到应用[1-3].

预应力混凝土连续梁桥或刚构桥通常使用变截面箱梁，对桥梁的设计和分析多基于平面杆系的有限元理论，通过划分为理想的单元用空间杆系理论进行分析，而且多是对桥梁纵向方向的研究.近几十年以来，交通运输量在不断增加，桥梁需要承受的荷载等级不断提高，桥梁的负荷越来越大[4-5]，特别是对于大跨径的混凝土箱梁桥，由于箱梁跨中底板厚度一般较小，在检测中发现，较多桥箱梁底板会具有不同程度的纵向裂缝等不良现象.

文中以一座实际工程桥梁为基础，对其进行有限元数值模拟，分析合龙束径向力的横向效应对箱梁底板的影响，指出底板纵向裂缝的主要原因，并通过与荷载试验相比照，对防止措施的合理性进行验证.

1 工程概况

某预应力混凝土变截面箱型连续刚构桥，主桥跨度为85 m +450 m +85 m.箱梁在墩部支点的梁高是9 m，在跨中和端部支点的梁高是3 m，箱梁底板上缘按二次抛物的形式变化，底板下缘按1.6次抛物的形式变化.桥梁主桥使用C50混凝土，桥面铺装使用10 cm厚的现浇C50混凝土.荷载等级为汽车-超20级、挂车-120.

在该桥跨中发现箱梁底板裂缝生成最多，有18条纵向裂缝，其中最大的裂缝长度为1.3 m，最大缝宽为0.60 mm；而在其他节段处，也有多条裂缝出现，见图1.

图1 底板纵向裂缝

2 预应力束作用机理

变高混凝土箱梁底板曲线通常按抛物线的形式变化[6-7]，在运营过程中，底板混凝土产生纵向开裂和向下崩出问题.合龙束通常沿箱梁底板线形布置为曲线预应力束，与直线束的作用机理有所区别.

直线束主要通过锚固段对构件传力，而曲线束则通过张拉变形对孔道挤压使混凝土产生预应力，见图2.曲线预应力可等效为两部分荷载：①使底板下压的径向力；②使底板上拱的切向拖曳力.

图2 预应力束等效荷载

图3为预应力束作用机理，令空间曲线预应力束位置方程为

r={x(s),y(s),z(s)}t

(1)

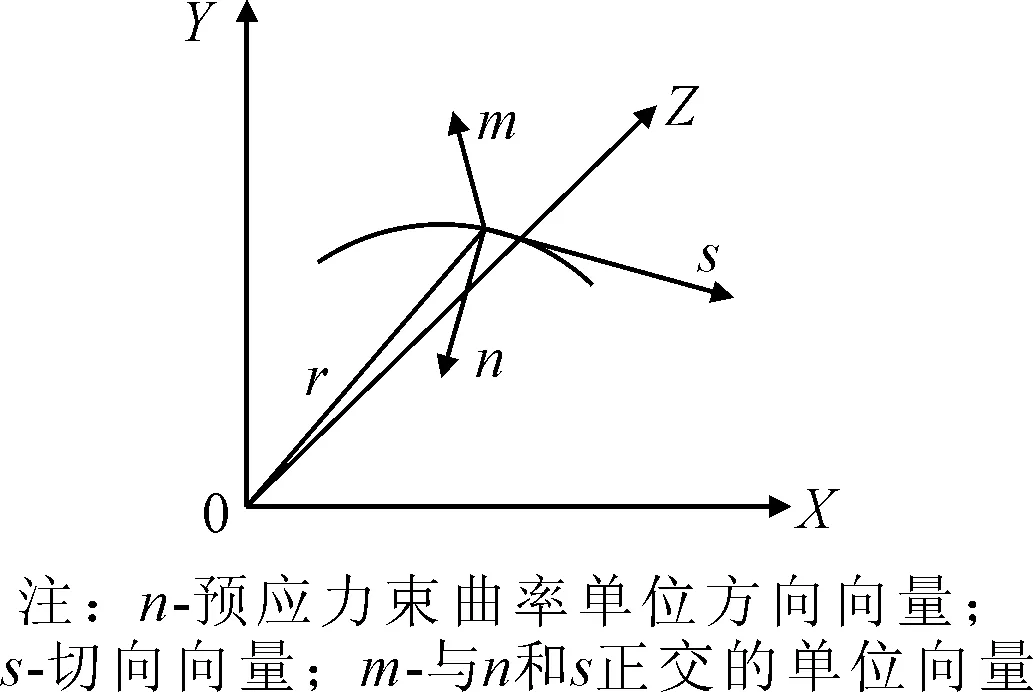
图3 预应力束作用机理

在预应力束上任取一微段ds，来分析预应力束的受力状况.令此微段中点处预应力束中拉力为Ts，由于预应力损失不可避免，则微段两端的张拉力为

(2)

由平衡关系得：

(pnn+pss+pmm)ds=0

(3)

式中：pm，ps，pn为张拉过程中微段在相应方向上所受的外力分量，pn即为是底板有下压作用的径向力.

展开式(3)，得

(4)

设k为s点曲率，则ds/ds=kn，故有

(5)

可得：

(6)

以上推导结果表明，合龙束在构件中主要产生两种效果力，包括径向挤压力和切向拖曳力.研究表明，对于预应力箱梁，由于预应力束与孔道之间的摩擦系数一般为0.15～0.30，切向拖曳力对箱梁底板受力状况的影响一般不到径向力产生的作用的5%[8-10]，故可不考虑.而预应力束的等效径向力为

q=pn=-kTs

(7)

式中：k为曲率半径.故箱梁底板预应力束的曲率半径越大，预应力束对构件的径向力q越小.

图4a)为连续梁合龙束示意图，等效荷载包括张拉力F、向上与向下的径向力分别用q1和q2表示.径向力对箱梁产生的效果使底板中央承受正弯矩，底板两边在腹板的弹性支撑作用下产生负弯矩，在底板纵向中心线附近会出现最大横向拉应力，在底板与腹板交接处产生较大的压应力，如果底板横向正截面承载能力不足易会产生纵向裂缝，见图4b).

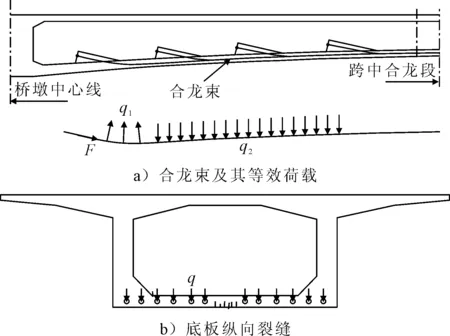
图4 合龙束等效荷载与底板纵向裂缝示意图

3 有限元建模

桥梁主桥主要由C50混凝土、预应力钢筋及钢板构成，其物理性质参数包括弹性模量、泊松比、密度等，见表1.

表1 材料参数

基本条件假定：①截面上的混凝土、钢板和钢筋的应变在梁受弯后，符合平截面假定；②钢筋与混凝土之间充分粘结，无相对滑移、变形协调；③钢板与混凝土接触面之间粘结可靠，无相对滑移变形.

混凝土使用Solid65实体单元模拟，考虑材料非线性，选择多线等向强化模型(MISO)，使用《混凝土结构设计规范》中的混凝土单向受压的应力应变关系为

(8)

式中：ε0为应力峰值所对应的应变，通常近似地取为0.002；E0为混凝土初始弹性模量；Es为最大应力点处割线模量，近似取为初始弹摸的1/2，下降段不考虑.钢板选取Solid45实体单元模拟，预应力钢筋使用link8杆单元模拟，钢筋与钢板应用双线随动强化模型(BKIN)模型.应力-应变关系见图5.

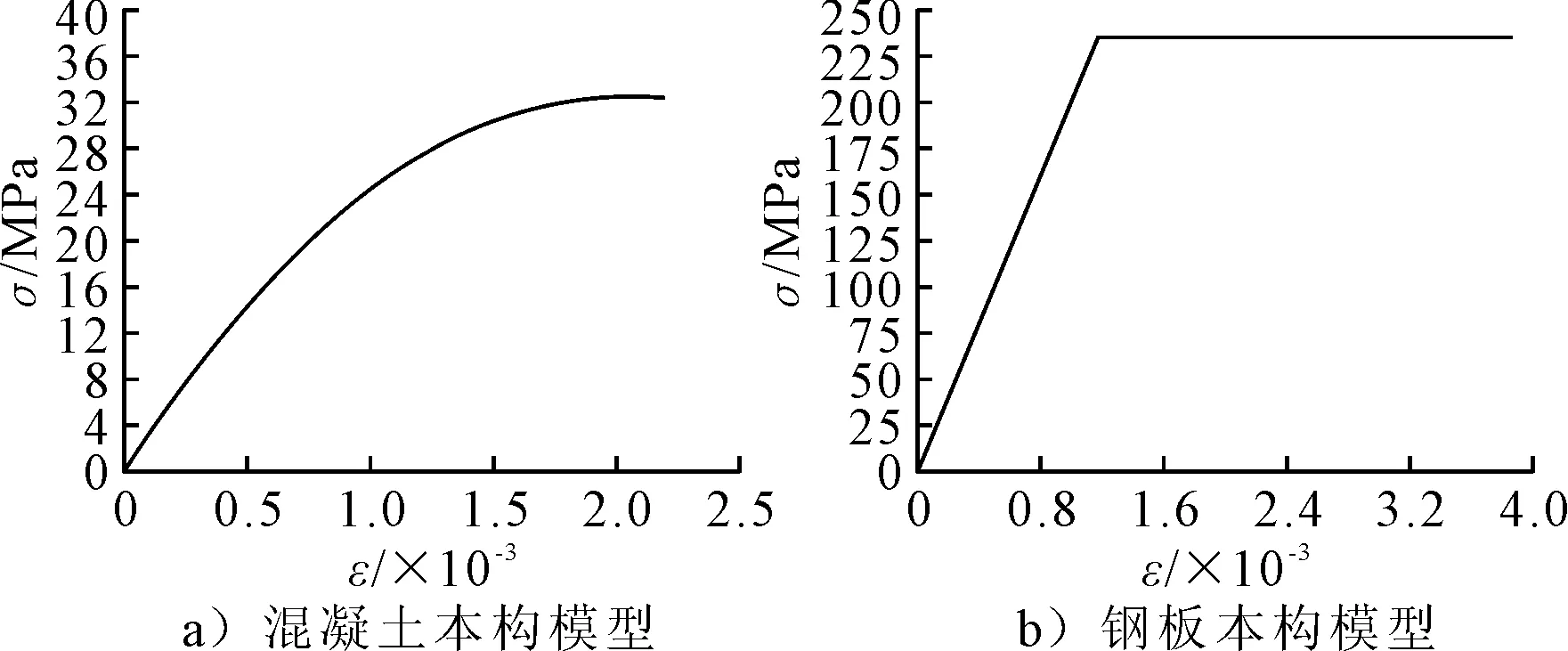
图5 本构模型

选取跨中合龙段及与合龙段相邻的三个节段进行局部实体有限元建模，考虑横向预应力同混凝土的共同作用，将钢筋与箱梁进行分开建模，独立划分网格，在混凝土单元与钢筋单元节点相近位置处进行耦合，达到共同作用效果.纵向和横向预应力钢筋采用Φs15.24(ASTM A416-87a标准270级，Rby=1 860 MPa)钢绞线，张拉控制应力为1 395 MPa.预应力通过降温法施加模拟.

为了更好的模拟边界条件，在主梁模型端部断面中性轴处建立两个节点，并与模型端部建立刚域，多选取一个节段进行虚拟梁单元模拟，梁单元一端固结，另一端连接在主节点上，并定义其刚度无限大，模型共计32 m.混凝土采用六面体网格划分，模型共计250 115个节点，211 716个单元.有限元模型、底板粘贴钢板后的模型及钢绞线分布见图6.

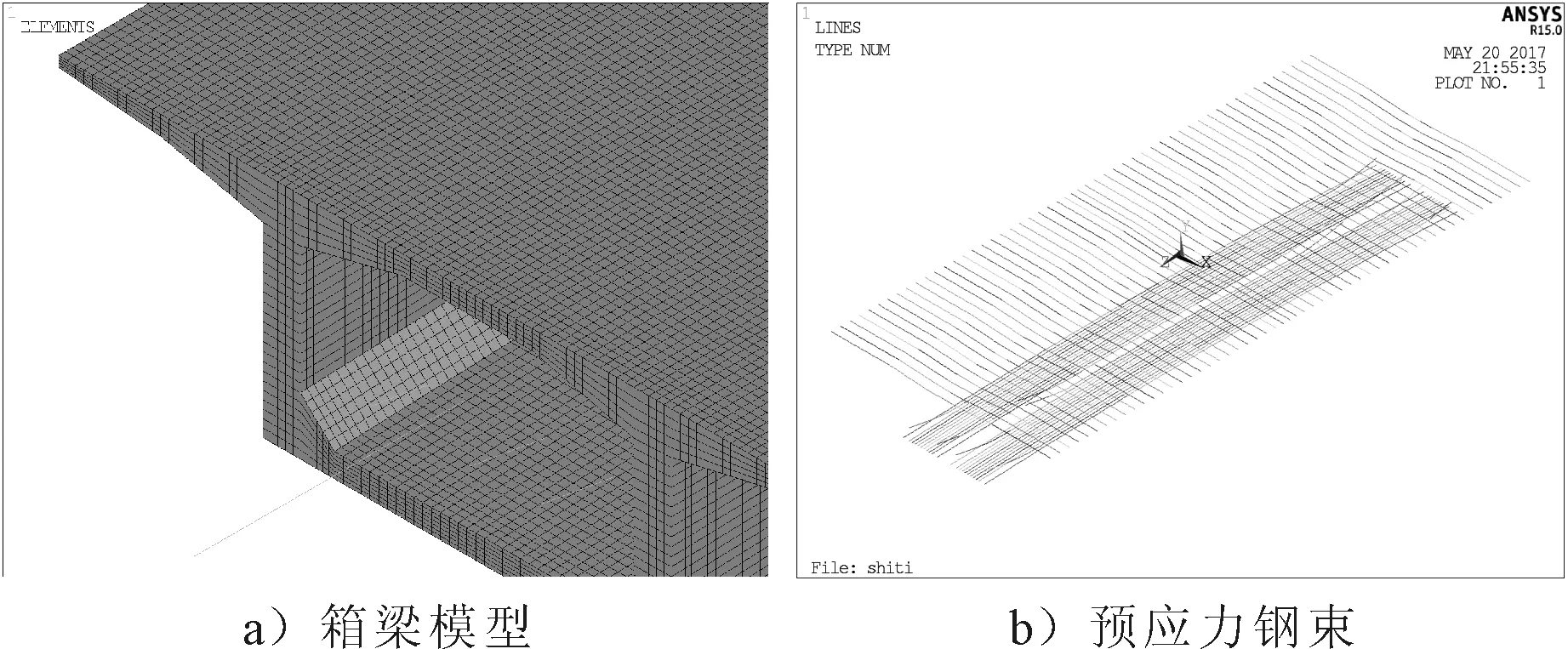
图6 有限元模型

4 计算结果分析

4.1 径向力横向效应分析

图7为合龙段节段处底板的横向应力分布云图和底板与腹板交接处的应力分布.由图7可知，底板中部沿箱梁横向方向处于受拉状况，应力最大达到为3.218 MPa；底板与腹板交接处拉应力达到3.121 MPa.

图7 合龙段底板横向应力分布云图

依据文献[11]，C50混凝土抗拉强度标准值为2.64 MPa，底板最大应力和腹板与底板交接处应力均大于混凝土抗拉强度标准值，这在桥梁长期运营中，对桥梁结构产生不利影响，是导致底板开裂的一个主要原因.

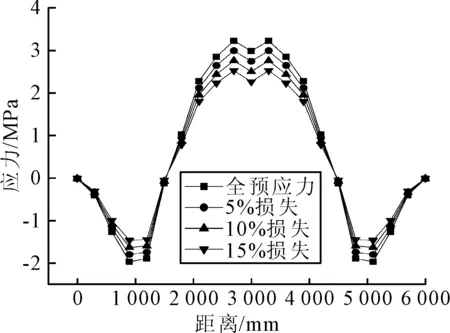
图8 跨中底板横向应力分布

图8为在全预应力状态下与考虑预应力损失在5%，10%和15%的状态下的跨中底板横向应力分布.底板中线附近承受横向拉应力最大，沿横向方向往两边拉应力逐渐减小，压应力增大，在离底板边缘左右两边0.9 m处位置，压应力达到最大，此后向两边逐渐减小到0.而随着张拉预应力的减小，底板横向最大拉应力逐渐减小.随着预应力损失的增大，箱梁底板横向应力随之降低，由式(7)可知，在桥梁底板线形一定的条件下，合龙束产生的径向力与正拉力成正相关.钢束对底板的径向力减小，箱梁底板横向应力有发生了明显减小的变化.预应力的径向力对导致底板纵向开裂有不可忽略影响.预应力束的径向力使箱梁底板中央产出较大的横向拉应力，底板两边在腹板处产生压应力，如果底板横向正截面承载能力不足易导致纵向裂缝的发生.

4.2 底板加固研究

目前，桥梁的加固维护工艺中，加固的主要方法有体外预应力索加固法、粘贴钢板加固法、粘贴碳纤维布加固法等方法，考虑到具体的现场及实际情况，本桥梁选择粘贴钢板加固法.粘贴钢板加固法具有施工工艺简单、受力均匀、不影响外观、加固效果显著等优点，相当于补充了梁体配筋，大幅度提高了桥梁的承载能力，能有效保护裂缝的发展，提高构件的整体刚度.

表2为在全预应力状态下，加固前与加固后合龙段处箱梁底板沿横向的应力分布，可以清晰的看出在相同的最不利荷载工况下，粘贴钢板后对箱梁底板受力有了良好的改善.加固前底板中部最大横向拉应力为3.218 MPa，底板粘贴钢板后为2.586 MPa，降低了0.632 MPa.底板沿宽度方向，加固前最大与最小横向应力的差值为5.19 MPa，加固后减小到4.44 MPa，明显改善了横向应力的分布情况.

表2 合龙段底板横向应力计算值

4.3 试验验证

对该桥进行荷载试验，选取跨中合龙段处截面为横向应力测试截面.加载前，对控制截面底板各应变测点布置电阻式应变片，应变片布置点见图9a)，工况为跨中最不利荷载工况，试验用车辆是400 kN双后轴载重车.

图9 应变布点及测试系统

在加载前、全部加载后和卸载后分别对各测点应变进行读数，然后根据材料弹性模量算出相对应的应力值.电阻应变测量采用DH3821静态应变测试分析系统进行采集，见图9b).现场应变测试结果见表3.

表3 应变测点实测值

实测数据与有限元计算结果见图10.由图10可知，粘贴钢板箱梁对底板横向受力情况有明显的改善，由于计算中采用全预应力，实际桥梁中存在预应力损失的原因，实测值与加固后计算值相比略微偏小.总体而言，试验测试所得应力值与加固后有限元计算结果数据吻合较好，符合混凝土设计规范强度要求，提高桥梁结构的承载能力，延长了桥梁的使用寿命.

图10 底板横向应力变化

5 结 论

1) 变截面预应力混凝土箱梁合龙束径向力的横向效应是导致合龙段底板纵向开裂的主要原因.它使箱梁底板中央承受正弯矩，底板两边在腹板处产生负弯矩，在底板纵向中心线附近会出现最大横向拉应力，在底板与腹板交接处产生较大的压应力，如果底板横向正截面承载能力不足易导致纵向裂缝的发生.

2) 合龙束预应力不合理也是导致底板产生横向裂缝的主要原因，优化预应力的张拉控制应力以及对箱梁截面的合理设计，能显著提高箱梁结构的承载能力.

3) 对旧桥底板的进行合理的粘贴钢板，可以起到有效的加固作用，提高旧桥的承载能力，延缓桥梁底板纵向开裂，增加桥梁的使用寿命.

[1] 项贻强,唐国斌,朱汉华,等.预应力混凝土箱梁桥施工过程中底板崩裂破坏机理分析[J].中国公路学报,2010,23(5):70-75.

[2] 潘钻峰,吕志涛.大跨径连续刚构桥主跨底板合龙预应力束的空间效应研究[J].世界桥梁,2006(4):36-39.

[3] 娄晟嘉,杨吉新.预应力混凝土连续刚构桥底板脱落成因分析[J].中外公路,2010(3):190-193.

[4] 李传习,柯璐,陈卓异,等.移动模架施工的PC箱梁悬臂段空间应力分析[J].桥梁建设,2016(5):77-82.

[5] 石雄伟,袁卓亚.钢板-混凝土组合加固预应力混凝土箱梁[J].长安大学学报(自然科学版),2012,32(3):58-62,90.

[6] ZHANG J. Field test and numerical simulation of cracks in the box girder of long-span RPC bridges[J]. Advanced Materials Research,2012(2):383-390.

[7] 黄亚新,张冬冬,赵启林.变高度预应力箱梁桥合龙段底板纵向裂缝的成因[J].公路交通科技,2011,28(11):76-84.

[8] XUN W, XIANSHUI Y, JIE L, et al. The crack resistance analysis in mid-span closure segment of continuous rigid-frame box girder bridge based on ANSYS[J]. IEEE,2014(4):987-990.

[9] 丁勇,赵启林,江克斌.PC箱梁桥底板横向应力计算方法及试验[J].长安大学学报(自然科学版),2011,31(6):43-49.

[10] 项贻强,唐国斌,朱汉华,等.PC连续箱梁合龙束横向效应[J].土木建筑与环境工程,2011,33(3):25-30.

[11] 中华人民共和国建设部.混凝土结构设计规范:GB50010-2010[S].北京:中国建筑工业出版社,2010.