不同凸形的高铁圆锥滚子轴承动态性能分析
李 铎 ,孙 伟 ,张 旭 ,杨帅杰
(1.大连理工大学 机械工程学院,辽宁 大连 116024;2.大连工业大学 机械工程及自动化学院,辽宁 大连 116034)
1 引言
高铁轴箱圆锥滚子轴承作为铁路车辆的关键零部件之一,其疲劳寿命的长短和使役性能的好坏直接影响到行车的安全[1]。在列车运行过程中,轴承滚子与滚道的接触区域会出现复杂的变形情况和应力集中现象。因此,设计采用特殊的滚子凸度来避免或降低滚动体应力集中现象、降低滚子与滚道接触作用力、减小轴承振动、提高轴承寿命就显得尤为重要。
目前对于高铁圆锥滚子轴承的凸度研究主要分为两种方法,一种是构建静力学模型,计算滚子滚道接触区域的力学性能[2-3];另一种是利用有限元软件建立静态受载下的有限元模型,进行滚子的应力分布分析。但是这两种方法都忽略了疲劳、振动等影响轴承使役性能的重要因素,因此也无法考虑滚子凸度的设计对于轴承动态性能的影响。基于以上原因,对圆锥滚子轴承的滚子凸度进行了研究,依照经验公式计算合适的凸度量,建立了四种不同凸形的高铁圆锥滚子轴承模型,并且基于LS-DYNA显示动力学分析软件,对由滚子凸形的改变而引起的圆锥滚子轴承动态性能的改变进行了仿真分析。
2 高铁轴承不同凸形的几何模型
圆锥滚子轴承凸度量的计算取决于轴承的实际受载情况和滚子的几何参数,因此根据高铁轴承的实际运行工况,依照经验公式,计算确定高铁轴承的凸度量,然后选取目前实际应用中高铁轴承的四种主要滚子凸形进行建模分析,分别为直母线型滚子、圆弧全凸型滚子、圆弧修正型滚子和对数曲线型滚子[4]。
2.1 直母线型滚子
传统的圆锥滚子轴承在设计时,滚子母线均采用直线,在加工制造时也尽量会把它们加工成圆锥面,以希望滚子受到的载荷能沿其母线方向均匀分布。但是由于在实际情况中,滚子与滚道的接触属于有限长的线接触问题,在接触区域中存在着严重的边缘效应,其滚子形状和接触区域应力分布,如图1(a)所示。因此,在实际加工中往往都会对直母线滚子进行修型。

图1 四种凸形滚子的几何结构Fig.1 Geometry of Four Kinds of Rollers
2.2 圆弧全凸型滚子
圆弧全凸型滚子的形状,如图1(b)所示。其滚子母线是一个具有固定表面曲率的圆弧,因此,圆弧全凸型滚子与滚道的有效接触长度会随着载荷的变化而变化。在轻载工况下,滚子与滚道的有效接触长度很短,近似于点接触,其接触区域为一个近似的椭圆,有可能会引起滚子的偏移及轴承的偏载,随着轴承所受载荷的增加,滚子与滚道间的接触长度会逐渐增大,偏载情况会有所改善。由图2可知,全凸型圆锥滚子的凸度量δ与滚子母线的曲率 R存在着如下的几何关系:R2=(R-δ)2+(L/2)2(1)

2.3 圆弧修正型滚子
由于圆弧全凸型滚子易在轻载的工况下出现偏载的问题,因此学者们设计制造了圆弧修正型滚子。圆弧修正型滚子的形状,如图1(c)所示。其滚子母线由一段中间的直线和两段直径较大的圆弧构成,滚子与滚道的有效接触长度可以达到滚子自身长度的70%左右,但是对直线与圆弧相交的过渡区的加工工艺提出了很高的要求[5]。圆弧修正型滚子的母线方程为:
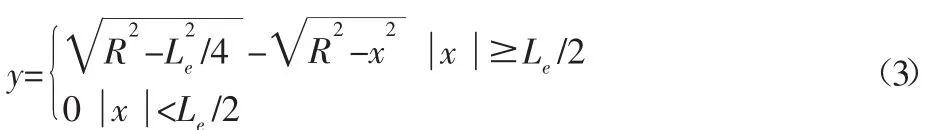
式中:Le—圆弧修正型滚子的有效接触长度;R=(L2-L2e)/8δ;δ=—受载最大滚子所受载荷。
2.4 对数母线型滚子
对数母线型滚子的形状,如图1(d)所示。其母线中间部分近似于直线,但在滚子的端部却变化很快。对数母线型滚子既能在轻载工况下的偏载问题,又能减小滚子两端的应力集中现象,其母线方程为[6]:
式中:E—接触副的综合弹性模量;v—泊松比;Qmax—受载最大滚子所受载荷。
3 高铁轴承有限元模型的建立
3.1 有限元网格模型建立
选用352228型高铁用圆锥滚子轴承进行分析,其结构参数,如表1所示。由于高铁轴承是双列圆锥滚子轴承,两列轴承的结构及材料属性都相同,为节约运算时间,在忽略轴承所受轴向力和轴向预紧的情况下,只对其中的一列进行建模[7]。由于高铁用圆锥滚子在实际工作过程中的运转情况以及有限元软件的运算特性,许多因素对于旨在分析的滚子凸度动态性能的影响可以忽略不计[8],因此,在仿真建模过程中做出了如下假设:(1)不考虑轴承倒角、游隙以及油膜厚度对轴承运行过程中的动态性能的影响;(2)高铁用圆锥滚子轴承的轴承座与轴承采用过盈配合连接在一起,载荷通过与内圈相配合的刚性轴进行传递,所以假设轴承外圈外表面与内圈内表面是刚性的;(3)忽略在仿真运算的时间段内,轴承的工作环境如温度、湿度、支撑刚度以及清洁度等对轴承性能的影响;(4)假设在仿真运算的时间段内,轴承的润滑剂的性能如密度、粘度等保持不变;(5)忽略轴承密封圈、防尘盖、润滑装置等零部件对轴承动态性能的影响。基于以上假设,分别建立了四种包含不同滚子凸形的轴承模型,轴承整体的有限元模型和四种不同的圆锥滚子有限元模型,如图2所示。

表1 轴承结构参数Tab.1 Structural Parameters of Bearing

图2 建立有限元模型Fig.2 Finite Element Model
3.2 材料模型参数
高铁用圆锥滚子轴承的内、外圈与滚子材料均为轴承钢。在轴承正常工作过程中,由于各部分接触时的变形量都很小,因此可以把圆锥滚子轴承的内、外圈与滚子均设置为弹性体,而内圈内表面由于和刚性轴相连,外圈外表面与轴承座相连,因此将内圈内表面和外圈外表面设置为刚性面[9]。相应的材料模型参数,如表2所示。

表2 轴承材料模型参数Tab.2 Material Parameters of Bearing
3.3 接触模型与载荷施加
由圆锥滚子轴承的结构和运转特性可知,轴承内部的元件之间一共包含三种接触,分别是滚动体和外滚道之间的接触、滚动体和内滚道之间的接触以及滚动体和保持架之间的接触。由于无法确定轴承在运转过程中的具体接触区域,因此将这三种接触均设置为面面自动接触对[10],设置滚动体与外滚道表面、内滚道表面的静摩擦系数为0.1、动摩擦系数为0.02,滚动体与保持架之间的静摩擦系数为0.05、动摩擦系数为0.005。假设外载荷与转速恒定,取轴承所受径向载荷为F=60kN,转速n=2000r/min,运行时间为0.1s。
4 高铁轴承不同凸形的动态性能分析
4.1 四种凸形滚子的接触应力分布分析
改善滚动体的应力分布情况、避免或降低接触区的“边缘效应”,是凸度设计的重要任务之一。因此比较了0.037s时四种不同凸形的滚子在相同运转工况下的接触应力分布,如图3所示。
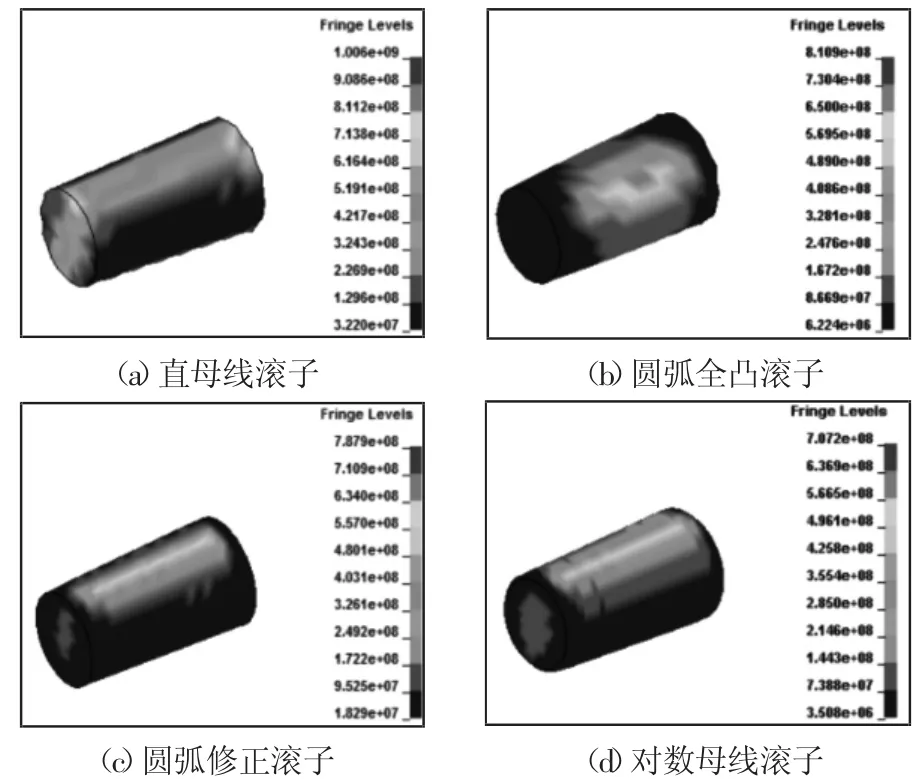
图3 四种不同凸形的滚子应力分布情况Fig.3 Stress Distribution of Four Kinds of Rollers
由图3(a)可以看出,直母线型圆锥滚子两端存在着严重的应力集中现象,最大应力出现在靠近内圈小挡边处,最大等效应力为1006MPa。
由图3(b)可以看出,圆弧全凸型滚子的两端没有出现应力集中现象,但滚子与滚道之间的有效接触长度非常短,接触区域为一个椭圆,接触压力按半椭球规律分布,滚子的最大压力出现在中部弧顶位置,最大等效应力为810.9MPa。
由图3(c)可以看出,圆弧修正型滚子在中间直线部分的接触应力分布比较均匀,而且在滚子的两端没有出现比较明显的应力集中现象,滚子的最大等效应力为787.9MPa,与圆弧全凸型滚子相比,在相同的工作条件下,圆弧修正型滚子的应力值较低,且应力分布情况有了极大改善,但是同时可以看出,在圆弧修正型滚子的母线圆弧与直线相交的部分,出现了明显的应力集中显现,虽然这种应力集中的产生包含着连接处有限元模型网格划分不精确的因素,但是仍对这种滚子实际生产中的加工工艺提出了很高的要求。
由图3(d)可以看出,对数母线型滚子的应力分布比较均匀,从滚子中心到端部的应力值逐步下降,与圆弧修正型滚子相比,由于滚子母线没有明显的突变区域,因此滚动体上没有出现明显的应力集中现象,滚子的最大等效应力为707.2MPa。
4.2 四种滚子凸形下的滚子-滚道作用力分析
滚子与滚道之间的作用力分析是圆锥滚子轴承零部件之间力学性能分析及寿命计算的一个重要考虑因素,选取某一在轴承中位置角固定的滚子,研究其在四种不同凸形情况下与滚道之间的作用力,得到滚子与外滚道作用合力曲线,如图4所示。由图4可以看出,圆锥滚子轴承运行过程中,滚子与滚道之间的作用合力表现出来很明显的非线性特征,由此可以推断,在轴承运转过程中,滚子与滚道的接触状态十分复杂,存在着十分明显的滚子与滚道接触时刻以及滚子与滚道的分离时刻。其中:(1)直母线型滚子与滚道之间的接触情况相对比较稳定,但是作用合力值非常大;(2)圆弧全凸型滚子与滚道的接触情况非常不稳定,存在着大量滚子与滚道分离的时刻,并且在滚子与滚道接触期间,作用合力的峰值突变明显,会导致滚子受到很强的突变作用力;(3)圆弧修正型滚子和对数母线型滚子的滚子滚道作用合力大小明显低于直母线型滚子和圆弧全凸型滚子,其中,对数母线型滚子的滚子滚道相互作用情况是四种凸形的滚子中最理想的。
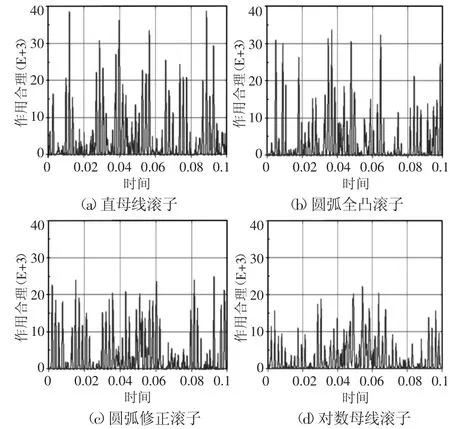
图4 四种凸形滚子轴承的滚子-滚道作用合力曲线Fig.4 Resultant Force Between Rollers and Raceways
4.3 四种滚子凸形下的轴承振动分析
圆锥滚子轴承在运转过程中的振动情况是衡量轴承使役性能的一个重要因素,在所设置的仿真条件下,轴承的振动情况可以通过内圈的加速度-时间曲线来衡量,因此,比较分析在相同的工况下,四种不同凸形的圆锥滚子轴承内圈在受载方向上的加速度变化,如图5所示。
图5 四种凸形滚子轴承的内圈加速度曲线Fig.5 Acceleration of Inner Ring
由图5可以看出,圆弧全凸型滚子轴承的内圈加速度曲线波动是最大的,其最大振幅达到454m/s2,这是由于圆弧全凸型滚子的滚子母线是一条曲率固定的圆弧,滚子与滚道为近似点接触,在运转过程中极易出现滚子偏转与轴承偏载的情况,因此轴承的内圈振动最为严重。直母线型滚子轴承的振动值仅次于圆弧全凸型滚子轴承,其最大振幅达到269m/s2,轴承内圈在运转过程中同样存在着严重的径向跳动。相比于前两种凸形,圆弧修正型滚子和对数母线型滚子的内圈加速度有明显改善,其最大振幅分别为247m/s2和259m/s2,并且从图5中易于观察出,圆弧修正型滚子轴承的内圈加速度曲线更为理想,其在最大幅值以及波动均值上都明显优于对数母线型滚子轴承。
4.4 四种滚子凸形下的滚动体平稳性分析
滚动体的运动情况十分的复杂,既包括绕轴承轴线的公转运动,又包括其绕自身轴线的自转运动,同时还易出现偏转、打滑及窜动等现象,因此,滚动体运动的平稳性是影响轴承运动平稳性的一个重要因素,而滚动体运动的平稳性可以通过滚动体上某一单元的位移轨迹来衡量,取四种不同凸形的滚子处于相同位置的同一单元进行分析,得到它们沿X轴方向的位移-时间曲线,如图6所示。由图6可以看出,在运转过程中,四种凸形的圆锥滚子均会出现不同程度的偏转和窜动,以X方向上的位移量为研究对象,可知,圆弧全凸型滚子的运动情况最不稳定,其曲线的最大幅值为0.58 mm,X方向上最大位移差值将近1mm,圆弧修正型滚子的运动情况则较为理想,其曲线的最大幅值为0.376mm,X方向上最大位移差值为0.59mm,相比于直母线型滚子和对数曲线形滚子,该凸形滚子的位移量下降了约22%,极大地提高了滚子的运行稳定性,进一步提高了轴承整体的运转稳定性。
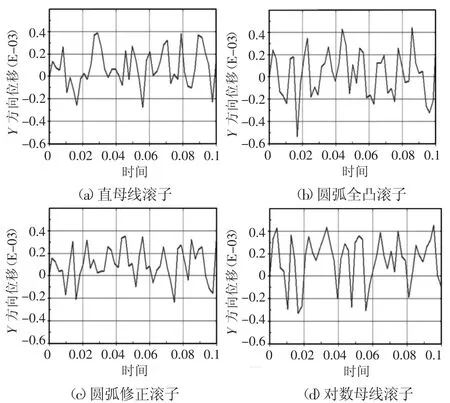
图6 滚子上某一单元的位移-时间曲线Fig.6 Change of Displacement of an Element on Rollers
5 结论
基于LS-DYNA显示动力学分析软件,分别建立了四种不同滚子凸形下的高铁用圆锥滚子模型,比较分析了他们在相同运行工况下的动态性能,对高铁圆锥滚子轴承的凸度设计具有重要意义。所得的主要结论有:(1)滚动体的不同凸形设计可以避免或降低直母线型圆锥滚子与内外圈接触处的应力集中现象,其中对数母线型滚子轴承沿滚动体母线方向的应力分布最为理想。(2)滚动体的不同凸形设计对滚子-滚道的相互作用力有着十分显著的影响,直接关系到轴承的疲劳寿命,其中对数母线型滚子-滚道间的接触情况和力学性能较为理想。(3)滚动体的不同凸形设计可以改善轴承的振动情况,进而影响轴承的运行平稳性,其中圆弧修正型滚子轴承的内圈振动情况最为理想,并可以有效改善滚动体在运转过程中的偏转和窜动。(4)选择滚子凸形时,应综合考虑滚子凸形对轴承的动态性能的影响。面对不同的设计需求时,应选择不同的滚子凸形。当以轴承疲劳寿命和设计准则时,应优先选用对数母线型圆锥滚子;当以轴承运行稳定性为设计准则时,应优先选用圆弧修正型滚子。
[1]范文明,邓立,孟庆江.铁路货车滚动轴承故障对行车安全的影响及防范[J].铁道技术监督,2004(4):35-36.(Fan Wen-ming,Deng Li,Meng Qing-jiang.Influences and prevention on driving safety of railway freight car rolling bearings’faults[J].Railway Quality Control,2004(4):35-36.)
[2]罗继伟.滚动轴承分析计算与应用[M].北京:机械工业出版社,2009:67-69.(Luo Ji-wei.Analysis Calculation and Application of Roller Bearings[M].Beijing:China Machine Press,2009:67-69.)
[3]王志伟,苗利军,孟玲琴.圆锥滚子轴承滚子凸度的优化设计[J].机械设计与制造,2014(6):55-61.(Wang Zhi-wei,Miao Li-jun,Meng Ling-qin.Optimal design of roller convexityoftaperedrollerbearing[J].MachineryDesignandManufacture,2014(6):55-61.
[4]张乐宜.高速铁路客车圆锥滚子轴承凸度及动态性能分析[D].洛阳:河南科技大学,2013.(Zhang Le-yi.Analysis on convexity and dynamic performance of tapered roller bearing for high speed railway coach[D].Luoyang:Henan University of Science and Technology,2013.)
[5]徐浩,汤勇,王大力.圆锥滚子轴承凸度设计[J].轴承,2003(9):6-8.(Xu Hao,Tang Yong,Wang Da-li.Convexity design of tapered roller bearing[J].Bearing,2003(9):6-8.)
[6]朱龙泉.铁路轴承的凸度设计及热应力分析[D].武汉:武汉科技大学,2012.(Zhu Long-quan.Railway bearings protruding degree of design and thermal stress analysis[D].Wuhan:Wuhan University of Science and Technology,2012.)
[7]Wang Zhi-wei,Meng Ling-qin,Hao Wen-si,Zhang E.Finite Element Method analysis and Optimal Design of Roller Convexity of Tapered Roller Bearing[J].Advanced Materials Research,2010(9):139-141.
[8]张刚,梁松,张义民.滚动轴承的动力学仿真分析[J].机械设计与制造,2013(9):32-34.(Zhang Gang,Liang Song,Zhang Yi-min.The dynamics simulation of the rolling bearing[J].Machinery Design and Manufacture,2013(9):32-34.
[9]朱成九,朱爱华,肖毅华.基于LS-DYNA铁路货车缺陷轴承动力学分析[J].轴承,2015(6):7-11.(Zhu Cheng-jiu,Zhu Ai-hua,Xiao Yi-hua.Dynamics analysis on defect bearings for railway freight based on LS-DYNA[J].Bearing,2015(6):7-11.)
[10]张乐乐,高祥,谭南林.基于ANSYS/LS-DYNA的滚动轴承仿真与分析[J].机械设计,2007(9):62-65.(Zhang Le-le,Gao Xiang,Tan Nan-lin.Simulation and analysis of roller bearing based on ANSYS/LS-DYNA[J].Journal of Machine Design,2007(9):62-65.)

