质朴扬新 开放统一 立意能力
——对一道中考压轴题的赏析
☉安徽安庆市宜秀区五横初级中学 戴向阳
(2017·安徽第23题)已知正方形ABCD,点M为边AB的中点.
(1)如图1,点G为线段CM上一点,且∠AGB=90°,延长AG、BG分别与边BC、CD交于点E、F.
①求证:BE=CF;
②求证:BE2=BC·CE.
(2)如图2,在边BC上取一点E,满足BE2=BC·CE,连接AE交CM于点G,连接BG并延长交CD于点F,求tan∠CBF的值.

图1
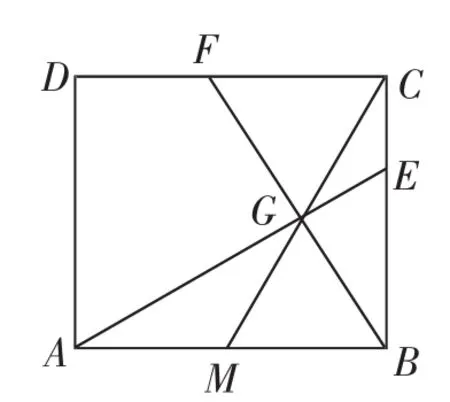
图2
二、特色解读
本题源于教材,低起点,高输出;解法多样,争奇斗艳;问题梯度分明,由易到难,思维水平逐级提高,使不同能力水平的学生到达问题的不同深度,体现了新课标关于义务教育阶段的培养目标的基本理念:“要面向全体学生,适应学生个性发展的需要,使得人人都能获得良好的数学教育,不同的人在数学上得到不同的发展.”
1.立题质朴,扬于创新,试题设计凸显了习题改编之道.

图3
本题取材于沪科版《义务教育教科书·数学》八年级下册第104页第9题:“如图3,在正方形ABCD中,点E、F是边BC、CD上的点,且BE=CF.那么,线段AE与BF的夹角有多大?为什么?”命题人别出心裁,巧妙地在此题中融合了新元素——“黄金分割”(沪科版《义务教育教科书·数学》九年级上册第68页例3),有效地将典型习题、教材例题同教材阅读与欣赏整合起来,借鸡生蛋,不愧是命题改编的典范之作.
本考题从逆命题角度对原题做了改造,得到第(1)①问.于考生而言,素材是熟悉的、亲切的,难点低,较之图3,图1只不过多了干扰“直观”的线条——CM.较之新定义问题,它没有因陌生符号或概念带来的压抑感,也没有因“定义”的新颖,给人兴奋与短暂的冲动.试题入口平淡如茶,考生对压轴题的畏难情绪得以释放,在心理上树立了答对问题的信心.考题起点低,平实无华,中、下水平的学生也易获得“成功感”.如果命题仅止于这点质朴,作为整卷压轴便失去了价值.命题者是烹饪高手,稍加“作料”——点M为边AB的中点,又烧出一道脍炙人口的考题(1)②.如此扬起了压轴题的层次,有效甄别了中等以上学生.然而考题似意犹未尽,对(1)②放宽条件,再拔新高,去掉中点M,逆向思考,遂成问题(2),试题难度再次“高温发酵”,至此,考题对“学优生”与“中等生”具有了鲜明的区分度,拉大了不同能力考生的考分差距,试题的甄别功能豁然明朗.本道考题的命制过程,正好彰显了几何试题改编与创新的途径:立于课本典型习题,或强化条件,或弱化条件,或逆向思考,或挖掘一般性,或驻足特殊性,或整合例题和习题,或伸向教材阅读材料.一道好的考题,常常是在质朴中扬新,一道备受青睐的压轴题,追求的当是低输入、高输出.
2.解法开放,千秋统一,在简练解法的探求中分享函数奇彩.
一道乐于称道的考题,不但体现在设计上,还表现在解法上既互异又统一.不同方法中有着统一,在统一中障显着异彩,差异与统一交相辉映.本题解法开放多样,使不同“学力”的人,能立足于自身的认识结构,形成不同的解法.对于第(1)①问,解题入口明朗,考生的解法主体上都统一在寻求△ABE≌△BCF上.不同之处,在证角的途径上略有差异,限于篇幅这里不再一一罗列.对于第(1)②问,解题入口比较隐蔽,但解法也主要在集中统一于证明△CGE∽△CBG,只是在寻找角相等的细节上与CG=BE时略显千秋,至于其他方法大同小异,不过绕得很,这里亦不再例举.对于问题(2),中考参考答案给出了两种差异显著的解答,鉴于过于复杂,本文也不再赘述.笔者不满于参考答案的烦琐,经过一番探索,分别从几何和代数角度找到两种相对简练的解法,在此以飨读者,分享函数奇彩,不当之处希不吝赐教.
解法1:如图4,过M点作MN∥BC,则有△CGE∽△MGN,所以
因为BE2=BC·CE,所以

图4

图5
由BE2=BC·CE,知E是BC的“黄金分割点”,从而即tan
解法2:令正方形的边长为1,以AD为y轴、AB为x轴建立平面直角坐标系,如图5所示.
由BE2=BC·CE,知E是BC的“黄金分割”.又BC=1,所以故E
3.立意能力,彰显素养,发挥“基本活动经验”与“几何直观”在解题中“指挥棒”的作用.
本题以质朴立题,在“移步换景”与角度变换中创新试题,突出了新课标的要求——“由知识立意向能力立意转变”.波利亚曾说过:“解题的成功要靠正确思路的选择,要靠从可以接近它的方向去攻击堡垒,为了辨别哪一个思路正确,哪一个方向可接近它,就要试探各种方向和思路.”所以每道题的解答,都需要解题者在未知情形下去探索,从认知结构中的“基本活动经验”出发,寻求解题思路,发挥好“基本活动经验”与“几何直观”在解题中“指挥棒”的作用.
解题能力是在亲身的实践中潜移默化形成的.学生的能力起于“基本活动经验”,行于“数学直观”,成于分析和推理,熟于思维方式,收于基本思想.对于第(1)①问,证线段相等,想到三角形全等,去寻找全等的条件,这是解决线段相等的“基本活动经验”之一.再如求证BE2=BC·CE,“基本活动经验”有:把乘积式化成比例式,寻求三角形相似,以及用等量线段替换,在问题串中前一问往往对后一问具有“垫脚砖”的作用;在探索相似过程中,必要时需根据直观添加辅助线.在“基本活动经验”的指引下,几何思考与“几何直观”如影相随,一边分析一边推理.如在“基本活动经验”确定证明△ABE≌△BCF时,“几何直观”与分析和推理同栖同飞,证明全等需要什么条件?图中有吗?能在推理中抵达目标吗?同样对于第(1)②问,证△CGE∽△CBG时,也经历了相同的追问思考.在经历了第(1)题两小问的充分探索与思考后,思维业已成熟,成熟的思维很快意会到第(2)问需要寻找相似,需要添加辅助线.这一思考流程,正是考生能力的再现.解法1是停留在几何层面的思维方式,是基于中考参考答案的反思与优化;而解法2,在思维方式上是一种突变:从几何思维方式转变为代数思维方式,在解题者眼中“线”不再是几何上的“线段”,而是代数上的函数图像,这是深层“基本活动经验”的唤醒.解题之奇,源于“线段”到函数图像基本经验的建构,出于思维方式之奇,收于思想方法之变.
本题立意充分体现了《中国学生发展核心素养总体框架》中“科学精神”之素养.
三、教学导向分析
中考题的命制方向对平时教学起着导航与理念转变的作用.本道试题对数学教学有哪些启示呢?概括起来,可用四个放眼来描述.
1.放眼教材.
一些好的中考题,多以教材为本,从教材的例题、习题中挖掘演变而来.日常教学中,要理解每一道例题、习题的价值,灵活地对有“曲度”的试题进行变式、拓展或改造,拓宽学生的眼界、拓长思维的深度、延伸认识的统一,从而举一反三,解一题通一类.
2.放眼课标和核心素养框架.
教学要研读课标,明重点、清难点,知哪些需深挖、哪些点到为止、哪些需补给、哪些要远足,把握节奏,需慢就慢.要吃透并理解核心素养框架要求,认真落实六大核心素养.
3.放眼实践.
能力,是个体在实践中形成的,教练教游泳,掌握的是写在书本中的知识,只有下水,才能学会游泳.能力是靠学习实践中“基本活动经验”的建构来形成的.解题能力,也只有在解题中构建“基本活动经验”才能形成.所以数学教学,先让学生自己学,教师再介入,进行指导纠正.那种先灌输再练习的做法,缺失的是“基本活动经验”的建构过程,学会的永远是模仿和套用.
4.放眼学生.
决定数学能力的关键是思维方式和思想开放度.思维迥异、思想开放的人才不会畏首畏尾,不会受惯性绑架,这是创新型人才一个突出的标志.所以教学中,不要过早抛掷结论,不要冷对学生质疑,不要用“理所当然”冷视学生热情,要善待学生发出的不和谐的声音,视学生是一个可以共商大计的人.

