深入挖掘结论，逐层拓展应用——以中考几何探究题为例

☉江苏连云港市东港中学 董海荣

以考查学生基础知识、逻辑思维能力及基本数学活动经验为背景的几何探究题在近年的中考中出现的频次很高，题型取材于课本教材，拓展性强、创新性高，具有选拔优质考生的功能，同时该类题对于初中教学具有指导意义.

一、真题解析，试题点评

1.真题呈现.

（2017年河南中考卷第22题）如图1，在Rt△ABC中，∠A=90°，AB=AC，点D、E分别在边AB、AC上，AD=AE，连接DC，点M、P、N分别为DE、DC、BC的中点.

（1）观察猜想.

图1中，线段PM与PN的数量关系是________，位置关系是________.

（2）探究证明.

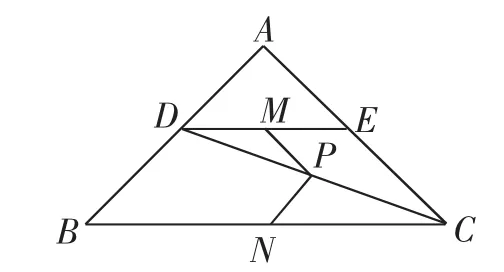
图1

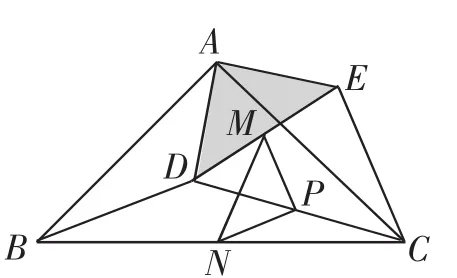
图2

把△ADE绕点A逆时针方向旋转到图2的位置，连接MN、BD、CE、MP、PN，判断△PMN的形状，并说明理由.

（3）拓展延伸.

把△ADE绕点A在平面内自由旋转，若AD=4，AB=10，求△PMN面积的最大值.

2.试题解析.

分析：（1）利用三角形中位线定理可判断BD=CE.利用三角线的中位线可得两直线平行，进而利用平行线的性质可推断结论.（2）先判断△ABD≅△ACE，进而可得BD=CE，利用（1）的方法可得即PM=PN.（3）可先判断MN最大时，△PMN的面积最大，进而求得AM，可得出MNmax=AM+AN，结合面积公式可得出结论.

解：（1）略.

（2）根据旋转性质可知∠BAD=∠CAE.又因AB=AC，AD=AE，所以△ABD≅△ACE（SAS），所以∠ABD=∠ACE，BD=CE.同（1），利用三角形中位线定理可得PN=即PM=PN，所以△PMN是等腰三角形.同（1），得PM∥CE，PN∥BD，所以∠DPM=∠DCE，∠DPN=∠DCB，利用角度转化可得∠MPN=∠ACB+∠ABC.又∠ACB+∠ABC=90°，则∠MPN=90°，所以△PMN是等腰直角三角形.

（3）同（2）可得△PMN是等腰直角三角形，所以MN最大时，△PMN的面积最大.MNmax=AM+AN.连接AM、AN，如图3.在△ADE中，可求得在Rt△ABC中，可求得所以

图3

3.试题点评，思路剖析.

本题为几何综合探究题，该类题一般设置发现猜想、思考探究、拓展应用三个阶段，从简单或特殊的问题入手，从而获得特殊情形下的结论，然后将该结论拓展迁移到较为复杂的问题，主要考查学生对几何基础知识的掌握及探究归纳能力.本题利用中位线定理及相关性质，确定了特殊情形下两直线的位置和数量关系，然后将其应用到三角形形状判断问题中，最后对其拓展延伸，应用到求几何面积的最值.整个过程环环相扣，逐步推进，解题思路也应准确把握要探究的结论，利用结论的特殊性、便利性解题.

二、试题链接，思路分析

几何探究题具有浓重的探究特性，问题设置步步深入，以探究为基础，以应用为目的，使结论的拓展性与应用性完美融合，其解题思路为结合符号、图形两种语言，利用几何性质，充分挖掘基本结论，利用联想、类比等方式逐层思考，拓展应用.

试题1：（2016年四川达州中考卷第24题）有△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B、C重合），以AD为边在AD右侧作正方形ADEF，连接CF.

（1）观察猜想.

如图4，当点D在线段BC上时，

①BC与CF的位置关系为：_______；②BC、CD、CF之间的数量关系为：_______.

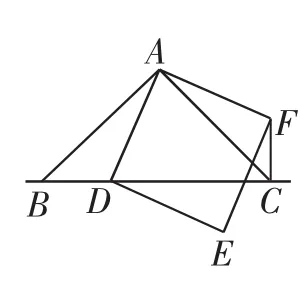
图4

图5

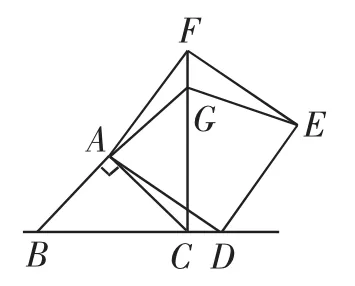
图6

（2）数学思考.

如图5，当点D在线段CB的延长线上时，结论①和②是否仍然成立？若成立，请给予证明；若不成立，请写出正确结论再给予证明.

（3）拓展延伸.

如图6，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE.若已知请求出GE的长.

分析：（1）①由正方形性质可得∠BAC=∠DAF=90°，可推△DAB≅△FAC，由全等性质可得结论（.1）②△DAB≅△FAC，根据三角形全等的性质可得CF=BD，∠ACF=∠ABD，由余角性质可得结论（.2）∠BAC=∠DAF=90°，推得△DAB≅△FAC，由三角形全等的性质可知仍然成立（.3）取BC的中点H，连接AH.作EM⊥BC，垂足为M.由等腰三角形的性质得进而可求DH，由正方形性质可得∠ADE=90°，AD=DE，利用矩形性质可得相关边和角的性质，可证△ADH≅△DEM，利用其性质可推得△BCG为等腰三角形，结合勾股定理可求GE的长.

试题2：（2017年江苏盐城中考卷第26题）（1）探索发现.

如图7，为一张直角三角形纸片，∠B=60°，小明想从中剪出一个以∠B为内角且面积最大的矩形，经多次操作发现，当沿着中位线DE、EF剪下时，所得矩形面积最大，随后他通过证明验证了其正确性，并得出：矩形的最大面积与原三角形面积的比值为_______.

图7

图8

（2）拓展应用.

略.

（3）灵活应用.

如图8，有一块“缺角矩形”ABCDE，AB=32，BC=40，AE=20，CD=16，小明从中剪出了一个面积最大的矩形（∠B为所剪出矩形的内角），求该矩形的面积.

分析：（1）利用中位线的性质及∠B=90°可知四边形FEDB为矩形，从而可求相关边的关系，求的比值，可以利用面积公式，以及边的关系来简化.（3）补全ABCD为完整矩形，可求相关边长，利用三角形全等，结合“探索发现”的结论可求该矩形的最大面积.

上述问题均为几何探究题，是对观察、猜想、分析、验证、归纳的探究过程的充分体现，在结构上每小题之间既相互独立，又紧密关联，对于学生的思维拓展具有积极作用.试题1猜想发现了两边之间的数量关系和位置关系，并对其进行深入思考，拓展应用；试题2则是探究发现了关于几何面积的比值关系，然后将其应用到较为复杂的问题中，解题过程都是有效利用探究归纳的结论，充分利用几何性质，辅以图形，拓展应用.

三、解后反思，教学思考

1.关注课本，夯实基础.

几何探究题涉及的知识点较多，熟练掌握几何基础知识是解决问题的关键.在几何复习阶段也不应颠倒学习重心，错误地将精力过多放在题海中，而应重温课本，夯实基础，梳理知识脉络，掌握知识间的内在联系和逻辑关系.对于教材中的重点、难点、易错点，要结合课后习题，可以利用文字语言、符号语言、图形语言来充分释义，引导学生探寻问题的一般解法.对于具有代表性、解法通性的问题，应进行总结归纳，促进学生知识完整性的构建，为学生的长远发展打下基础.

2.注重关联，提升能力.

几何探究题的各部分具有鲜明的关联性和递进性，难度依次递增，主要考查学生思维的层次性，在教学中教师要注重初中知识的初始教学，有效结合教材内容，精心设置具有关联性的问题，由浅入深，逐层递进，引导学生有意识进行思考，对于一些具有创造性的见解和思路，要加以鼓励和支持，培养学生的学习兴趣，激发学生的探究热情，然后辅以相应的解题方法，指导学生的解题过程，提升学生的解题能力.

3.经历探究，发展思维.

探究型问题关注学生的思考过程、推理过程，主要考查学生的逻辑思维能力，因此在几何教学中，要注重培养学生的猜想推理和递进推理能力，通过有针对性的教学活动让学生经历知识探究发现、拓展应用的过程，促进学生数学思维的发展，同时给学生留足思维的空间，通过操作实践、猜想验证等方式促进学生思维的拓展性，借助探究题的开放平台，使学生的知识掌握和技能形成完成良好的融合，初步发展学生的创新意识.

四、写在最后

对于初中的几何探究题，要从基础知识入手，结合几何性质归纳总结简单问题的特性结论，然后加以拓展应用.在教学中，教师要引导学生关注教材，学习问题的通性、通法，夯实基础；设置具有关联性和递进性的问题，促进学生解题能力的提升；针对性开展教学活动，让学生经历数学的探究过程，促进学生的思维发展和创新意识的形成.

1.居建斐.熟而不俗 余味悠长——“基于教材，高于教材”的中考探究题赏析［J］.中学数学（下），2016（8）.

2.严亚琴.摭谈一道平面几何题的解法探究与启示［J］.中学数学（下），2017（12）.

3.戴回娟.关于初中数学探究式教学实验的思考［J］.数学教学通讯，2017（26）.

4.石小江.初中数学“图形与几何”中的合情推理研究［J］.数学教学通讯，2017（8）.