示波法血压测量技术研究进展

【作 者】龙韬臣，巨建树，李德玉，张弛北京航空航天大学生物与医学工程学院，北京市，100191

0 引言

血压是人体重要的生理参数，能够反映人体心脏和血管的功能状况，是临床上诊断疾病、观察治疗效果、进行预后判断的重要依据。血压测量的最精确方法是进行有创测量，然而这种方法具有侵入性，因此大多数情况下我们所说的血压测量技术都是无创测量[1]。

现如今的无创血压测量方法主要有：柯氏音方法[2]、示波法[3]和基于脉搏波传播速度[4]的方法。示波法又称为振荡法，是临床上各类监护仪、电子血压计广泛采用的血压测量技术。其测量血压的原理为：在使用袖带充放气测量血压的过程中，随着袖带压力的下降，袖带内会出现一个压力振荡波，从袖带压力振荡波中利用特定血压估计算法可获取人体肱动脉血压值。这种方法的优势在于：①袖带内并不需要拾音器件，操作简单，抗外界噪声干扰能力强，而且不会像柯氏音方法那样受到外界环境的影响；②袖带脉搏波是血管受到外界持续变化的压力后的反映，相比前两种方法，其除了反映血压信息外还可能包含血管的顺应性和血管体积等心血管参数信息[5]。

本文将对示波法血压测量中的关键技术进行概述，其中包括袖带压力波的前处理方法和血压估计算法。前处理方法可分为振荡波包络的提取和去干扰两个部分；血压估计方法则包括：传统示波法、基于波形形态学方法、基于模型的方法和基于数据的学习型方法等。我们将对这两部分进行简单介绍并对其优缺点进行讨论，最后对基于示波法的血压测量技术进行展望。

1 前处理方法

在进行血压估计前我们需要从原始的气压信号中提取出振荡波信号或振荡波包络，因此振荡波/包络的提取是进行血压估计的重要步骤。振荡波的噪声源主要包括传感器引入的高斯白噪声、身体移动和肌肉搐动引起的运动噪声以及呼吸干扰等，而血压估计算法的性能高度依赖于振荡波的信号质量，因此对于实际数据进行去噪处理也就变得至关重要。这部分我们主要对血压估计算法前的预处理步骤和去干扰方法进行讨论。

由实测数据到包络数据的预处理方法一般有两个过程：实测数据到振荡波，振荡波到包络。一般认为实测数据的信号模型为：原始数据=袖带放气数据+袖带振荡波，根据袖带放气数据变化缓慢以及振荡波变化快的特点，可以提取出袖带振荡波。振荡波的获取可以分为：频域滤波和趋势去除。两种方法并没有本质区别。对于振荡波到包络的过程，值得探讨的地方是对包络的定义。有些论文的横坐标是时间，而有些则是压力；而对于纵坐标的定义则更加多样，包括峰值—基线差、峰值—谷值差、包络斜率、波形面积等[6]。还有论文直接根据希尔伯特变换来提取包络，总之，对于包络的定义并不统一。

前面对预处理过程进行了分析，但在预处理过程中需要进行去噪。一种通用的去干扰方法是对提取出的包络进行曲线拟合，如多项式和高斯曲线拟合[6]。然而这种方法存在问题，就是拟合函数对原始曲线有多大的逼近程度将决定最终估计算法的准确度，如果拟合函数不够准确，血压估计算法将会受到影响。对于特定的干扰其处理的方法并不相同。针对运动伪迹这种和期望信号存在频谱重叠的干扰，需要一些现代的信号处理算法来解决。其中对包络数据进行去运动伪迹的方法有：四阶回归模型、卡尔曼滤波和模糊逻辑等。但如果要对整个振荡过程进行跟踪，则需要对整个振荡波信号进行波形估计。这其中包括自适应滤波、粒子滤波等方法。呼吸干扰对信号存在加性，幅度调制和频率调制三个因素的影响，同时呼吸信号是一种准周期的谐波信号，因此其去除的方法必然和运动伪迹的干扰去除方法不同。去除呼吸干扰的方法包括：Taylor-Fourier transform、频域滤波、同态滤波和小波脊等。

对于信号的前处理部分提出的方法很多但并不统一，对于强调血压估计算法的研究对信号前处理方法要求并不高，或者是利用一些简单的前处理方法，而对于强调前处理方法的文献则会突出前处理方法对最终血压估计结果的影响。因此很难去评判是否具有一个最优的前处理方法组合，研究者应该根据自己的实际信号在当前的前处理方法上进行一定的选择或者提出最为适用于自己实测信号的前处理方法。

2 估计方法

利用振荡波进行血压估计的物理机制为在放气过程中，当袖带压力大于收缩压时，完全受压的肱动脉段处于闭塞状态，由于股动脉段受压不均匀，此时检测到的振荡波是由不完全受压的肱动脉冲击袖带而成，因此只能检测到微弱的振荡波信号；当袖带压力降低到平均压时，动脉管壁呈去负荷状态，振荡波幅度达到最大值；当袖带压小于舒张压时，动脉血管充分扩张，血管管壁刚性增强，此时的振幅同样微弱。基于以上原理，检测得到的振荡波（或振荡波包络）的时间（或压力）序列应该包含有血压相关信息。近些年很多学者对基于示波法的血压测量技术进行了开发，特别是渥太华大学的Mohamad Forouzanfar[7]团队从多角度对基于示波法的血压估计算法进行了扩展。目前基于示波法的血压估计算法大致可以分为：传统示波法、基于波形形态学方法、基于模型的方法和机器学习方法。

2.1 传统示波法

目前基于示波法的血压估计算法应用最为广泛的是幅值系数法。幅值系数法认为血管的平均压等于外界压力时振荡波包络幅度最大，由此可以获得平均动脉压，通过特定的比例系数和可以获得收缩压和舒张压。由于获得的包络数据是一些离散点且包含随机干扰，因此有文献指出，直接根据包络幅度最大值判断平均压的方法并不准确，其提出通过直线拟合振荡波包络两边的曲线获得平均压[8]。同时，通过研究大量的样本，收缩压和舒张压比例系数的变化范围分别为[0.45 0.73]，[0.69 0.83][9]。目前对幅度系数法的改进基本上也集中在对比例系数的确定。传统示波法中还有一类方法是根据包络波的斜率/拐点来判断收缩压和舒张压，不过这种方法对噪声和干扰十分敏感，一种改进的策略是利用二阶AR模型进行平滑后判断[10]。

总之，传统示波法操作简单，运算量小，但均存在一些问题。对于幅值系数法，由于个体血压、血管顺应性等的差异，收缩压和舒张压的获取很难仅仅通过一个比例系数就能准确确定，因此其未来的发展趋势应为具有个体差异性的比例系数选择方法；对于拐点法则方法本身不鲁棒，容易受到干扰，如何更加稳定地进行血压估计是其发展方向。

2.2 基于波形形态学的方法

在整个示波法测量血压的过程中，已有的大多数方法都是基于原始数据变换到包络数据后再进行血压估计的，然而这样的处理仅仅是提取了振荡波的幅度信息而对于振荡波中的波形信息进行了选择性丢失。不难理解振荡波的波形特征在示波法测量血压的过程中存在变化，实质上这种波形特征的变化和常用的包络幅值变化有颇多相似之处，都是压力—特征的序列，只是目前尚未能够对某种波形特征变化进行一个清晰且易于计算的定义，不过很多研究者都在进行这方面的努力。

Abolarin D[11]做了最直观的尝试，通过提取振荡波中的各谐波分量的幅值和相位获得多个特征和压力的函数。Marom O[12]提出一种 S-积分方法，它认为在寻找到平均动脉压之后，利用平均动脉压所对应的振荡波积分和时间间隔的比值即为收缩压的幅值，而两者之差就是舒张压的幅值，在这里研究者明显利用的就是振荡波波形面积信息。还有研究者利用了wald 检验方法来寻找波形形态上的急剧变化点，以此来判断收缩压和舒张压[13]。有些研究者更进一步，其提出的硬度系数、反射系数和外周强度系数都利用了振荡波波形进行计算，并得到了这些系数和压力的变化关系[14]。

正如开始所说，从波形形态学获取血压信息是一个很好的思路，然而目前的波形形态学方法仍然存在较大的问题。首先是对于目前提出来的几个波形特征变化无法进行生理学上的解释，更为重要的是目前这些方法并没有得到充分的验证。以后的发展方向可能是通过生理或者信号处理尝试提取更具有表征能力的特征。

2.3 基于模型的方法

基于生物力学原理建立物理模型是心血管研究的常用手段。对示波法的整个血压测量过程进行数学建模，一方面能够对血压测量过程中的血管状态，袖带内的气体振荡波的形成进行定量的物理解释，另一方面能够指导和一定程度检验基于袖带气压波形的血压估计算法。现在对基于示波法的血压测量过程的数学模型主要分为两类：① 建立全身的心血管模型，在肱动脉处增加变化的袖带压力对血流的阻力作用[15]。此模型实现了心血管和袖带力学两个系统的耦合，能够反应外界力学作用对全身血液流动的影响，然而此模型涉及到较多的参数，并不容易从模型实现血压的求解。② 假设袖带仅仅对血管体积产生影响，血管内的压力波没有发生变化，对在袖带作用下的上肢肱动脉进行建模。此模型能够对已有的一些血压估计算法进行机理解释，同时具备血压估计的潜力。

基于模型的方法最重要的是建立跨臂压Pt和血管体积V的关系模型，如公式(1)。其中跨臂压Pt的定义为袖带内压力Pc和血管内压Pa的差值，当跨臂压Pt≥0和Pt＜0时血管体积和跨臂压Pt之间的关系处于两个不同的物理状态[16]。其它如袖带压力模型，袖带压力和体积关系模型都能够用较简单的关系表示[17]。

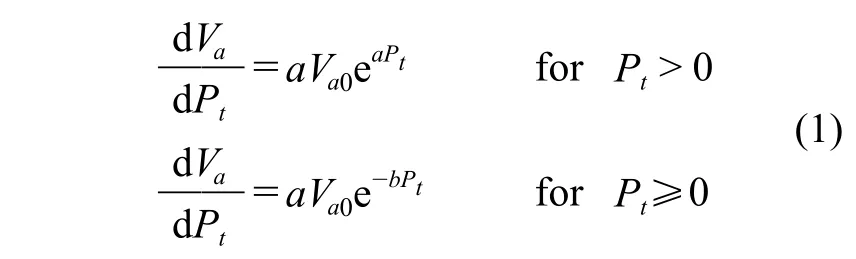
其中Va表示血管体积，Va0表示当跨臂压等于0时的血管体积，a、b分别反映血管处于压缩和膨胀状态的顺应性系数。

模型方法为血压估计提供了一个全新的思路，它能够对采集到的振荡波进行生物力学解释，同时能够求解出除血压外的其它心血管参数，如血管顺应性和血管体积。然而现有的对整个血压测量过程的数学模型实际上并不完善。例如：①模型假设测量过程中血压不发生变化；②模型的血压估计结果并没有体现出优势且优化求解的计算复杂度相比传统方法却大大增加了。对于模型方法以后的发展方向可以从两个方面看，一方面是建立更为准确的物理模型，另一方面是减少模型中的不必要参数和简化模型，降低寻优算法的计算复杂度。

2.4 机器学习方法

由于这几年互联网数据量的急剧增长，Deep Learning方法在语音、图像识别领域取得巨大成功[18]，同时基于数据驱动的算法开始应用于很多传统信号处理领域，如语音增强。由于机器学习算法具有很强的适用性，只要能够获得足够的数据，且模型能够对问题进行很好的近似，在理论上就能够得到较好的分类、回归和标记结果。同样，在血压估计问题上，也开始出现很多利用数据驱动的算法。

机器学习中一个很重要的步骤是特征提取，在血压估计的问题上也就是对振荡波包络进行特征描述。如：最大幅值对应坐标、包络持续时间、包络面积、最大幅值前的面积、最大幅值后的面积、最大幅值和持续时间比值等。然后是学习模型的选择，包括线性回归、支持向量机和神经网络等。当然还有更为直接的形式，直接将包络数据作为学习模型的输入[19]，两者的区别在于前者对数据进行了特征提取，模型训练相对容易，而后者则在数据量足够多的情况下，能够获得很好的结果。

机器学习的方法给很多需要建立物理模型的传统领域提供了不一样的思路，其算法脱离了具体的物理模型。不过，基于机器学习的算法存在一个很难解决的问题，即对于大数据量的依赖。在一般的科研中，我们很难获得足够的样本空间，这让机器学习算法很难实现。当然，机器学习算法无法解释血压测量的过程，因此对于算法的扩展性不强，在深耕专业领域时只能做到知其然却不知其所以然。

3 挑战和展望

目前基于示波法的测量技术，存在以下几方面的挑战：

（1）基于示波法的测量技术并不能进行血压的连续测量。人体血压是一个随时间变化的时序信号，个体在正常情况下一天的血压值都会随着情绪、运动量等发生变化，笔者在进行血压测量试验时静息状态下30 min内个体血压值存在约15 mmHg的变化，因此本质上来说进行血压的连续检测是更为合理的方式。然而目前基于袖带的血压检测方法均是假设在一段短时间内人体血压值没有发生变化，在一次血压测量过程中仅给出一个血压测量值。

（2）血压测量时在高压段存在不舒适感。目前的基于示波法的血压估计中，其采集过程均需要使袖带气压超过收缩压。在ICU或者其它需要对血压进行连续检测的情况下，不间断对病人进行加压超过110 mmHg会引起患者的不适感，同时在进行多次血压测量时会使病人出现循环系统重构现象。因此在进行血压测量过程中，如何在袖带加压最大值尽量小的情况下获得合适的血压估计值是目前示波法血压测量技术面临的重大挑战。

（3）肥胖、血管硬化、心率不齐等都会造成估计精度的下降。对于肥胖人群和血管硬化人群此时经典的示波法系数并不适用，而对于心率不齐患者则在血压测量技术中前处理部分的包络提取存在难度，因此血压估计精度仍需要持续关注。

从以上的分析看出，现有的示波测量技术仍需进一步的完善。其存在以下几个发展方向：

（1）直接从振荡波中提取出和血压相关的信息甚至获得一个血压时间序列是以后一个可长期关注的领域。现有的估计方法中除了波形形态学方法建立了振荡波波形和血压之间的关系外[11]，其它方法大多处理的是振荡波包络信号。然而正如前文已经提到的，振荡波信号包含有比包络更多的信息，而目前并没有得到充分挖掘。机器学习算法可以直接将振荡波信号作为数据源，利用DNN的中间层进行特征的提取。而对于基于模型的方法也可以考虑从振荡波开始进行最优化求解[20]，然而目前该方法仅存在于模型仿真阶段。以后可考虑利用目标跟踪的思路，类似于机器人领域的SLAM技术，对实际数据进行参数跟踪。

（2）多传感和多方法联合是提高血压估计精度的有效思路。联合ECG和振荡波可以形成类似PTT（脉搏波传播时间）的血压估计方法[21]；联合加速度传感器能够为干扰去除提供参考信号；而在估计方法方面，联合机器学习方法和传统幅值系数法能够获得统计最优的幅值系数从而进行最终的血压估计，以上方法的出现可看出血压测量技术中多信息融合的趋势。综合利用现有方法的优势，形成新的稳定且准确的统计融合方法将会是未来发展的有意义尝试。

（3）利用模型方法的预测能力进行基于部分包络信息的血压的估计，同时可从理论上解决血管硬化情况下血压估计不准确的情况。模型可以认为是一种先验知识，数据则是模型的体现形式。模型的重要价值在于在没有数据情况下本身就反映了事物的运行规律。从模型的应用潜力来看，在少量的数据条件下就能够反解出模型的参数。在已提出的血压测量模型中，利用部分包络数据同样可以求解出血压估计结果，虽然其估计准确性有待讨论，但其展现出了很好的研究和应用前景。同时，模型中直接包含有血管硬化相关参数，可以直接进行不同血管硬度人群的个性化测量。在模型完善建立的前提下，对于肥胖等人群，该方法具备通用个性化测量的发展前景。

总之，在示波法出现的近半个世纪以来，虽然其已在家庭医疗和临床上被大量使用，但很多机理和算法上的问题并没有得到充分解决，仍然需要学术界和工业界的共同努力对基于示波法的血压测量技术进行研究。

致谢：

本课题由国家自然科学基金（No. 11672026,11302019）和虚拟现实技术与系统国家重点实验室支持。

[1] Jones D W, Hall J E. Hypertension: pathways to success[J].Hypertension, 2008, 51(5): 1249-1251.

[2] 邓静. 柯氏音法与示波法结合的新型血压测量方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.

[3] 许怀湘, 房兴业. 采用示波原理间接测量血压方法的进展[J]. 航天医学与医学工程, 2000, 13(3): 231-234..

[4] 蒋巍巍, 季忠. 无创血压测量方法的研究进展[J]. 中华高血压杂志, 2015(7): 685-689.

[5] Antonova M L. Noninvasive determination of arterial elasticity and blood pressure. Part I: arterial volume pulsations and elastogram[J].Blood Press Monit, 2013, 18(1): 32-40.

[6] 温亮, 李振波, 陈佳品, 等. 基于高斯拟合的神经网络血压测量算法[J]. 传感器与微系统, 2014, 33(4): 132-134.

[7] Forouzanfar M. A modeling approach for coefficient-free oscillometric blood pressure estimation[D]. Ottawa, Canada:University of Ottawa, 2014.

[8] Medero R. Determination of oscillometric blood pressure by linear approximation: US, US5577508[P]. 1996.

[9] Chen S. Improving algorithms for oscillometric blood pressure estimation by suppressing breathing eあects[D]. Ottawa, Canada:University of Ottawa, 2010.

[10] 江国泰, 蒋大宗. 非创伤性血压测量的理想化力学模型及其参数辨识[J]. 中国生物医学工程学报, 1991(3): 167-173.

[11] Abolarin D. Non-invasive estimation of blood pressure using harmonic components of oscillometric pulses[D]. Ottawa, Canada:University of Ottawa, 2016.

[12] Marom O, Seidmann A. Standard algorithm for blood pressure measurement by sphygmo-oscillographic method[J]. Med Biol Eng Comput, 1996, 34(1): 82-83.

[13] Barbe K, Van Moer W. An innovative oscillometric blood pressure measurement: Getting rid of the traditional envelope[C]. MeMeA,2012: 1-6.

[14] Maf i M, Rajan S, Bolic M, et al. Blood pressure estimation using oscillometric pulse morphology[C]. EMBC, 2011: 2492-2496.

[15] Liang F, Takagi S, Himeno R, et al. A computational model of the cardiovascular system coupled with an upper-arm oscillometric cuあ and its application to studying the suprasystolic cuあ oscillation wave, concerning its value in assessing arterial stiあness[J]. Comput Meth Biomech Biomed, 2011, 16(2): 141-157.

[16] Babbs C F. Oscillometric measurement of systolic and diastolic blood pressures validated in a physiologic mathematical model[J].Biomed Eng Online, 2012, 11: 1-12.

[17] Ursino M, Cristalli C. A mathematical study of some biomechanical factors aあecting the oscillometric blood pressure measurement[J].IEEE Trans Biomed Eng, 1996, 43(8): 761.

[18] Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015,521(7553): 436-444.

[19] Colak S, Isik C. Blood pressure estimation using neural networks[C]. IEEE CIMSA, 2004: 21-25.

[20] Forouzanfar M, Balasingam B, Dajani H R, et al. Mathematical modeling and parameter estimation of blood pressure oscillometric waveform[C]. MeMeA, 2012: 1-6.

[21] Forouzanfar M, Ahmad S, Batkin I, et al. Model-based mean arterial pressure estimation using simultaneous electrocardiogram and oscillometric blood pressure measurements[J]. IEEE TIM,2015, 64(9): 2443-2452.