基于SE和C0算法的连续混沌系统复杂度分析
叶 晓 林, 牟 俊, 王 智 森, 金 基 宇, 张 蕾, 刘 恩 萌
( 大连工业大学 信息科学与工程学院, 辽宁 大连 116034 )
0 引 言
混沌理论是过去几十年来蓬勃发展的一门关于非线性动力学系统的科学,混沌现象无处不在,尤其在信息安全等领域的应用越来越广泛[1]。系统的复杂性是一个系统能否生成随机序列的能力,而复杂度的大小取决于待测序列随机程度。因此,近些年来科学界对关于混沌序列复杂度的算法问题越来越重视,各大研究机构也争相进入到研究混沌理论的热潮中。
算法复杂度一般可分为基于行为复杂度的算法(FuzzyEn算法[2-4]和SCM算法[5-6])和基于结构复杂度的算法(SE复杂度算法和C0复杂度算法)。时间序列复杂性越大,随机性越大,序列能够恢复成原序列越困难。所以在应用混沌系统时,本身应具有尽量大的复杂性,以确保扩频系统具有良好的抗干扰性和较强的抗截获性。
在20世纪中后期,Kolmogorov等[7]提出了序列复杂度特性的概念,同时也创立了Kolmogorov 复杂度算法。因为当时科技的局限,不能通过计算机来验证是否正确,只是粗略地提出并没有深入地研究。直到1976年,Lempel等[8]详细阐明了Lempel-Ziv算法,该算法也是Kolmogorov复杂度算法的升华,在生物工程、气象学和密码学等领域得到广泛的应用。20世纪末,Pincus等[9]创建了复杂度特性值近似熵的算法(ApEn)。2002年,Bandt等[10]阐明了复杂性度量排列熵算法(PE算法)的优越性。它作为ApEn算法的改良,在后来被科学界广泛的应用。
虽然Lempel-Ziv、ApEn、PE算法都可以准确地表征连续混沌系统的复杂性,但Lempel-Ziv算法仅仅对混沌序列的时间尺度简单估计,能够精确计算的也只有序列的长度大小,而且对于其非伪随机序列部分也要用软件来做细微处理;而ApEn算法处理不同嵌入维数的变化时,计算过程中涉及嵌入维数和分辨率参数问题,且得到的计算结果也受主观因素的影响;在应用PE算法时,计算结果受到很多因素的影响和限制。这3种算法在序列长度较短时计算速度较快,但当数据的长度增加到一定量时,其运算的速度随之变慢,所以实用性较低。对比这3种算法,利用谱熵法(SE)和C0算法基于傅里叶变换(FFT)计算熵,不仅计算速度快且能更好地体现序列的相关结构,同时也能更有效地测度系统的复杂性,尤其是在计算连续平稳时间序列时,SE和C0算法的优势更明显。
本研究应用SE和C0算法分析了Bao混沌系统[11-13]、Rossler混沌系统[14]、文氏桥超混沌系统[15]的复杂性曲线,并验证了其正确性。通过两个连续混沌系统和一个连续超混沌系统的相位图、李雅普诺夫指数谱[16]、周期分岔图、SE复杂性曲线和C0复杂性曲线等动力学方法的分析和比较,展现了混沌系统具有非常丰富的动力学特性,同时也证明了SE和C0复杂度算法在分析连续混沌序列复杂度特性上的优越性。
1 SE复杂度算法和C0复杂度算法
1.1 SE复杂度算法描述
SE算法[17]利用傅里叶变换域中的能量分布,基于香农熵算法得到谱熵值,其算法如下:
(1)去掉序列的直流部分:对长度为N的伪随机序列利用公式(1)去掉其直流的部分,使其频谱可以更准确地表现出信号的能量大小。
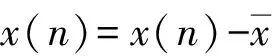
(1)
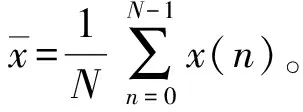
(2)对公式(1)进行离散傅里叶变换。
(2)
式中,k=0,1,2,…,N-1。
(3)计算相对功率谱:对经过离散处理后的X(k) 序列取其前半部分的序列参与计算,并采用Paserval算法,得出其中一个特定频率的功率谱大小为
(3)
式中,k=0,1,2,…,N/2-1。
序列的总功率可定义为
(4)
相对功率谱的概率可表示为
(5)

(4)利用公式(3)、(4)、(5),并结合香农熵概念,求得信号的谱熵se[17]为
(6)
如果公式(6)中Pk为0,则定义PklnPk为0。谱熵的大小收敛于ln(N/2),为了便于比较分析,可将谱熵归一化,得到归一化的谱熵为
(7)
通过以上变换可以看出,序列的功率谱变化情况越不稳定,结构组成越简单,其序列振幅越不明显。相应的,得到的测量值也较小。
1.2 C0复杂度算法描述
C0复杂度算法[18-20]主要思想是把序列分成规则和不规则的部分,所要的是整个混沌序列中的非规则部分所占的比例。具体计算步骤如下:
(1)对序列进行离散FFT变换
(8)
式中,k=0,1,…,N-1。
(2)去掉公式(8)非规则部分,假设{X(k),k=0,1,2,…,N-1}的方均值为
(9)
在公式(9)中加入一个参数r,留下超过该均方值r倍的部分,并假设剩余部分值为零,即
(10)
(3)对公式(10)作傅里叶逆变换
(11)
式中,n=0,1,…,N-1。
(4)结合公式(11),定义C0复杂度测度为
(12)
在FFT变换基础上发展出的C0复杂度算法,删除序列中的规则部分,保留了不规则部分,在整个序列中不规则部分越多,它对应的时域信号越接近随机序列,序列复杂性越大。
2 连续混沌系统的复杂度分析
2.1 Bao混沌系统复杂度特性
Bao混沌系统建模方程为
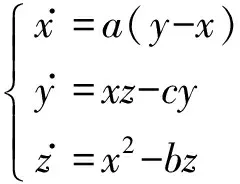
x.=a(y-x)y.=xz-cyz.=x2-bzìîíïïïï
(13)
取系统初值为(10,10,10),仿真步长为t=0.01 s。用SE和C0算法计算y序列的复杂度特性。Bao系统在a=20,b=4,c=31.5时,可以计算出相应的李雅普诺夫维数为2.150 5。Bao系统的吸引子在x-y平面的相图(图1(a)),随着参数b的变化,整个系统也在混沌态、周期态、稳定不动点等动力学状态间变换,由于Bao系统的最小李雅普诺夫指数恒小于-5,为了方便观察,只对两个相对大的进行分析研究。如图1(b)所示,Bao系统参数b在(0,12.6]的区间内,系统的李雅普诺夫指数只有一个大于0,表明在此区间内该系统处于混沌状态,当系统处于混沌态时的复杂度是该系统所有状态中最大的。李雅普诺夫指数越大,说明它的分离程度就越大,也就是说该系统复杂程度也越大。对应图1(d)和图1(e),当系统处于周期态时SE和C0复杂度最小,在b=1.281 和5.879时的两个周期窗口处最为明显,在实现保密通信时建议避免在以上两个邻域区间进行参数加密。在b>7.915后,随着b的增大,SE和C0复杂度呈现总体下降趋势,在b>9.422 后系统进入反倍周期分岔状态,这些和相应的李雅普诺夫指数谱、周期分岔图(图1(c))等验证结果一致。
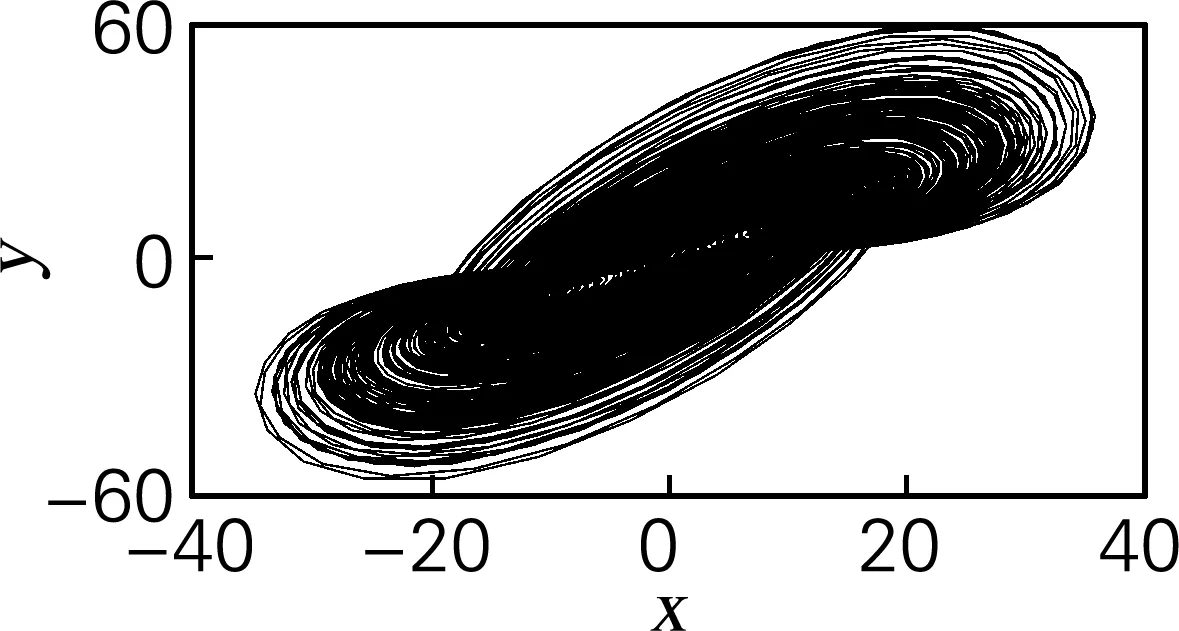
(a) x-y平面相图

(b) 李雅普诺夫指数谱
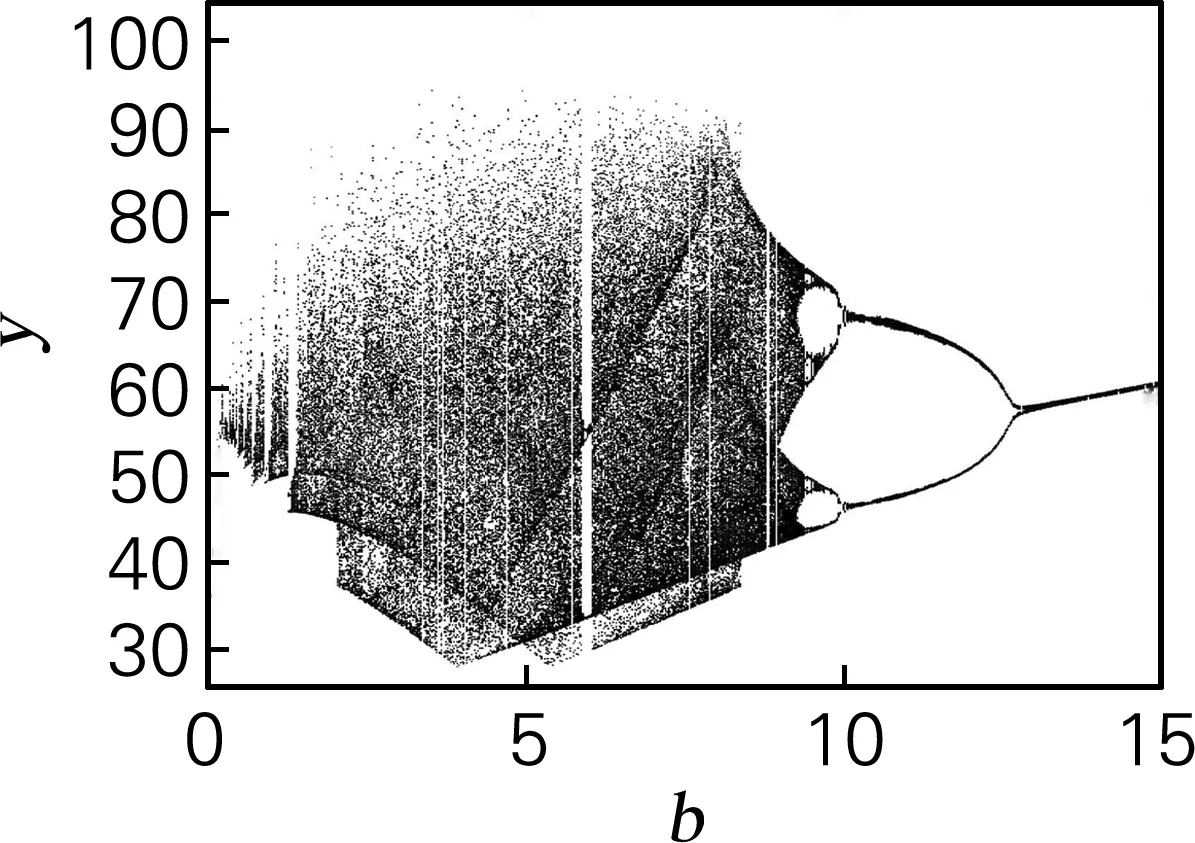
(c) 分岔图
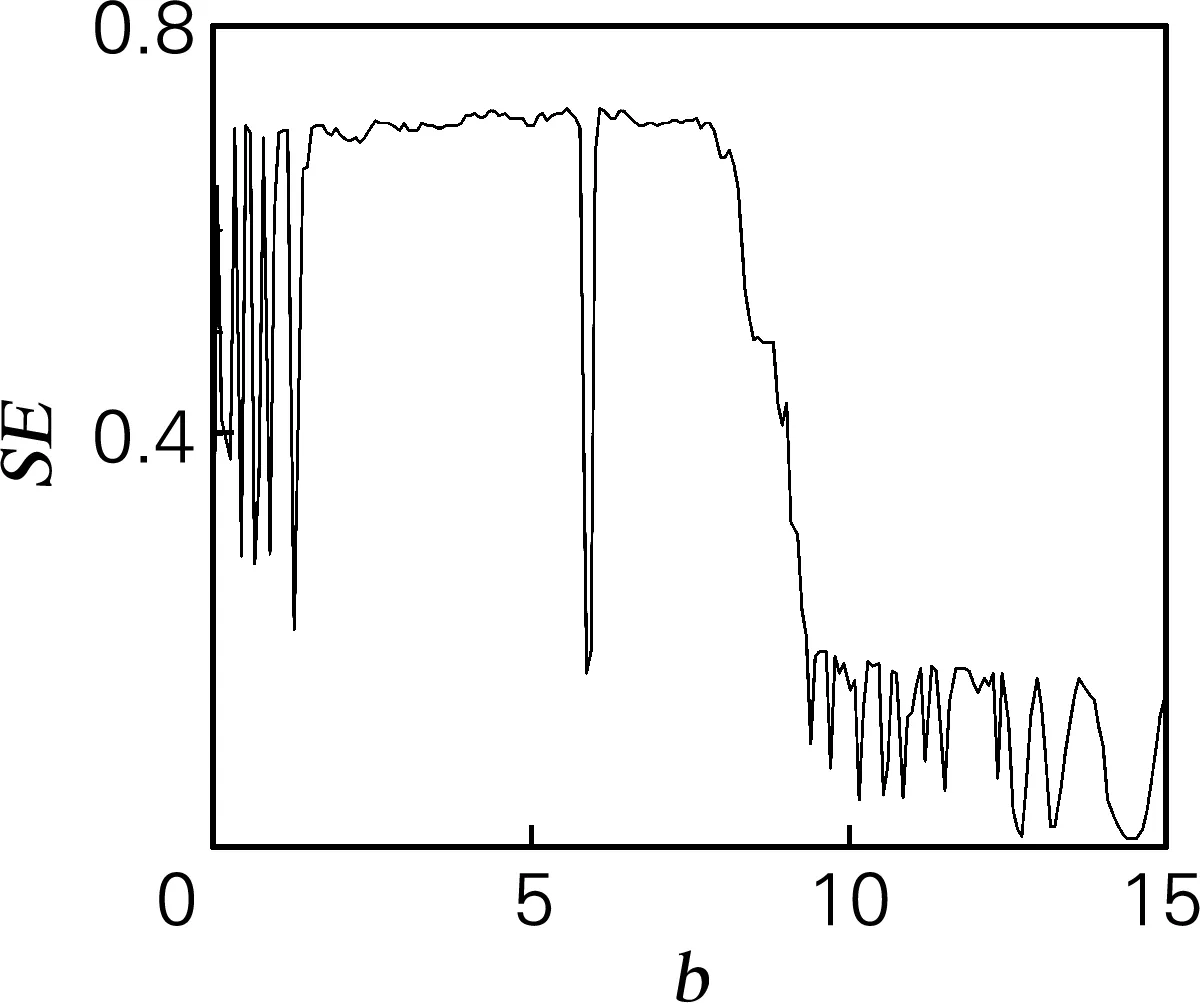
(d)SE复杂度
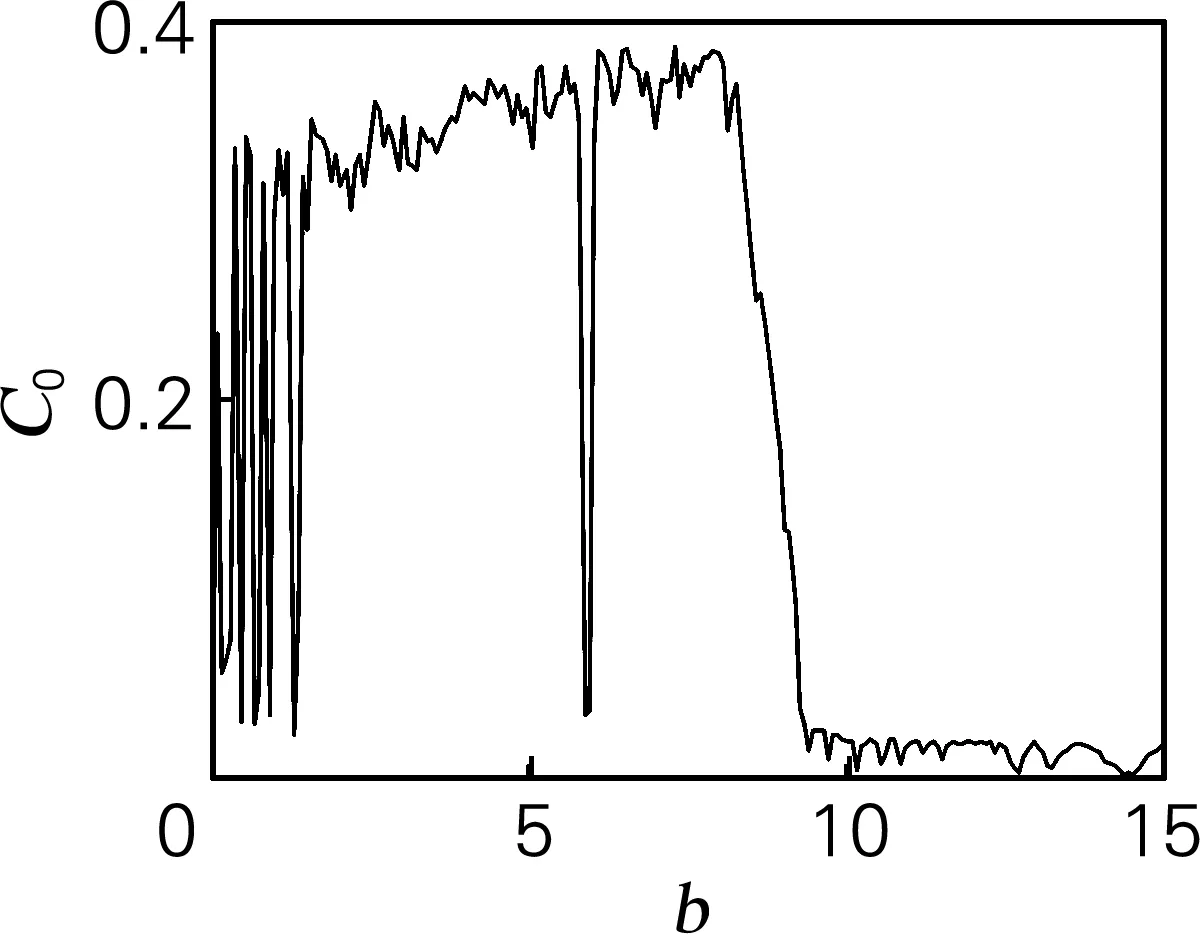
(e)C0复杂度
图1 Bao系统仿真结果
Fig.1 Simulation results of Bao system
2.2 Rossler混沌系统特性
Rossler混沌系统建模方程为
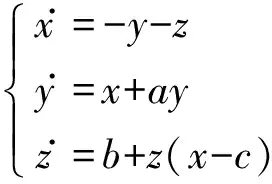
x.=-y-zy.=x+ayz.=b+z(x-c)ìîíïïïï
(14)
取状态变量初值为(0,0,0),仿真步长为t=0.01 s。用SE和C0算法计算y序列的复杂度特性。在a=0.19,b=0.18,c=5.7时的李雅普诺夫指数稳态值为LE1=0.101 5;LE2=0;LE3=-5.697 9,由此可以计算出相应的李雅普诺夫维数为2.0341。系统相位图如图2(a)所示。随着参数b的变化,系统的最小李雅普诺夫指数(图2(b)) 恒小于-2,所以保留了两个大的李雅普诺夫指数。在变量b=0.112和0.321处有两个最大的周期窗口,在这两个数值邻域内系统处于周期态。b>0.703时,整个Rossler系统处于反倍周期分岔态,这与对应的分岔图(图2(c))所呈现的结果一致。从Rosller系统的SE复杂度(图2(d))和C0复杂度(图2(e))也可以看出在系统处于周期态时复杂程度明显下降,处于混沌态时复杂度增大,仿真结果均与其所对应的李雅普诺夫指数谱、分岔图的实验验证结果基本保持一致。
2.3 文氏桥超混沌系统
文氏桥超混沌系统方程为

x.=(ab-1/a)x-ay-eHy.=abx-ayz.=-cw+ceHw.=dzìîíïïïïï
(15)
式中,H=x-z+0.5(|x-z-1|-|x-z+1|)。
文氏桥系统是一个超混沌系统,共有5个参数,其中参数b为变量。取仿真参数中初值为(1,1,1,1),仿真步长为t=0.01 s,用SE和C0算法计算y序列的复杂度特性。在a=0.55,b=7.95,c=0.95,d=42.5,e=30时的李雅普诺夫指数稳态值为LE1=1.151 0;LE2=0.092 5;LE3=-0.712 8;LE4=-50.389 4,由此可以计算出相应的李雅普诺夫维数为3.010 5。文氏桥超混沌系统混沌吸引子相图如图3(a)所示。当参数b变化时,李雅普诺夫指数如图3(b)所示,在3≤b≤4.1时,文氏桥系统处于周期态中;当4.1
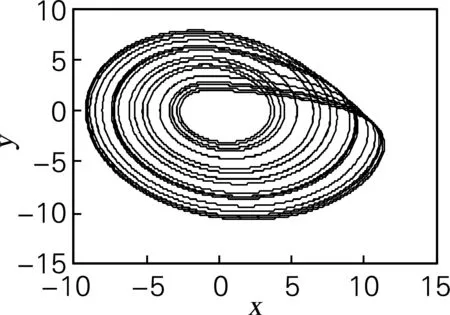
(a) x-y平面相图
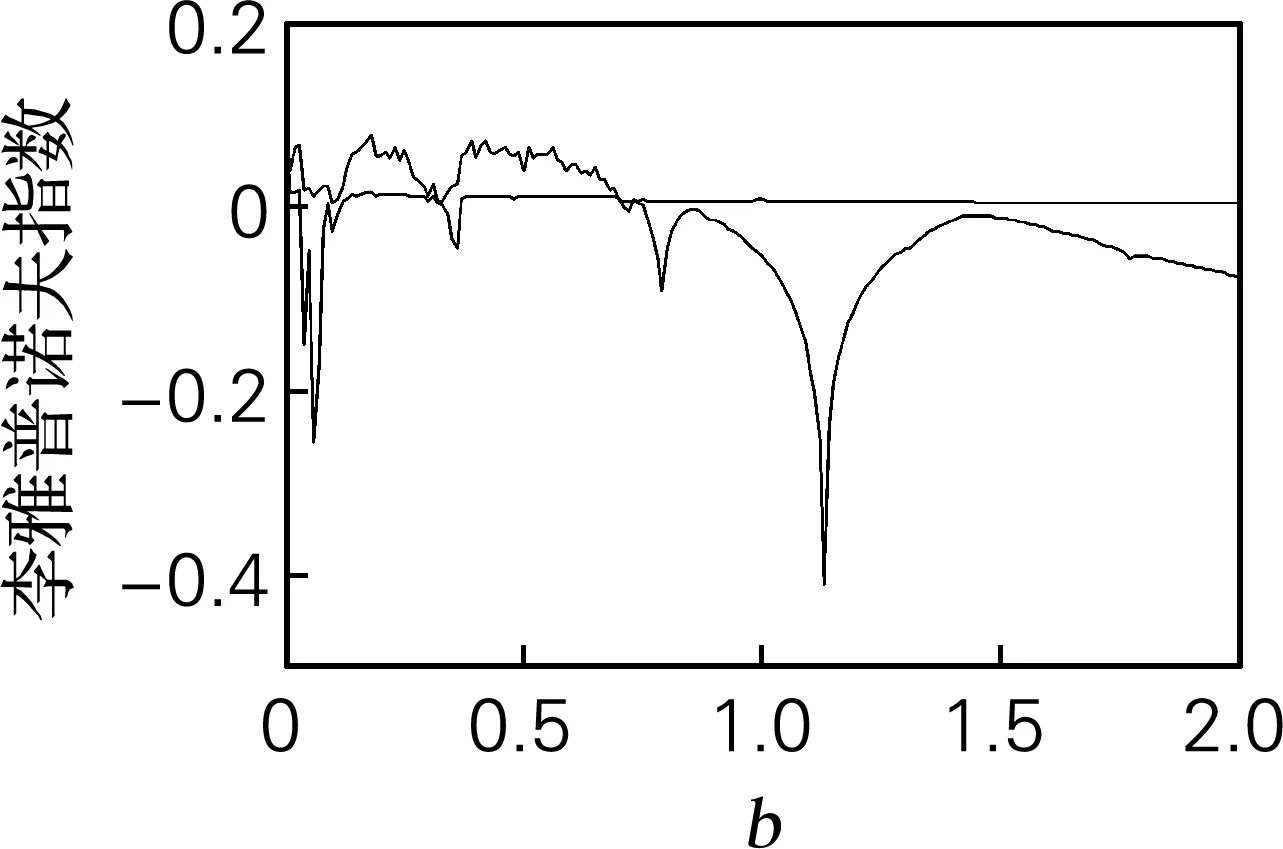
(b) 李雅普诺夫指数谱
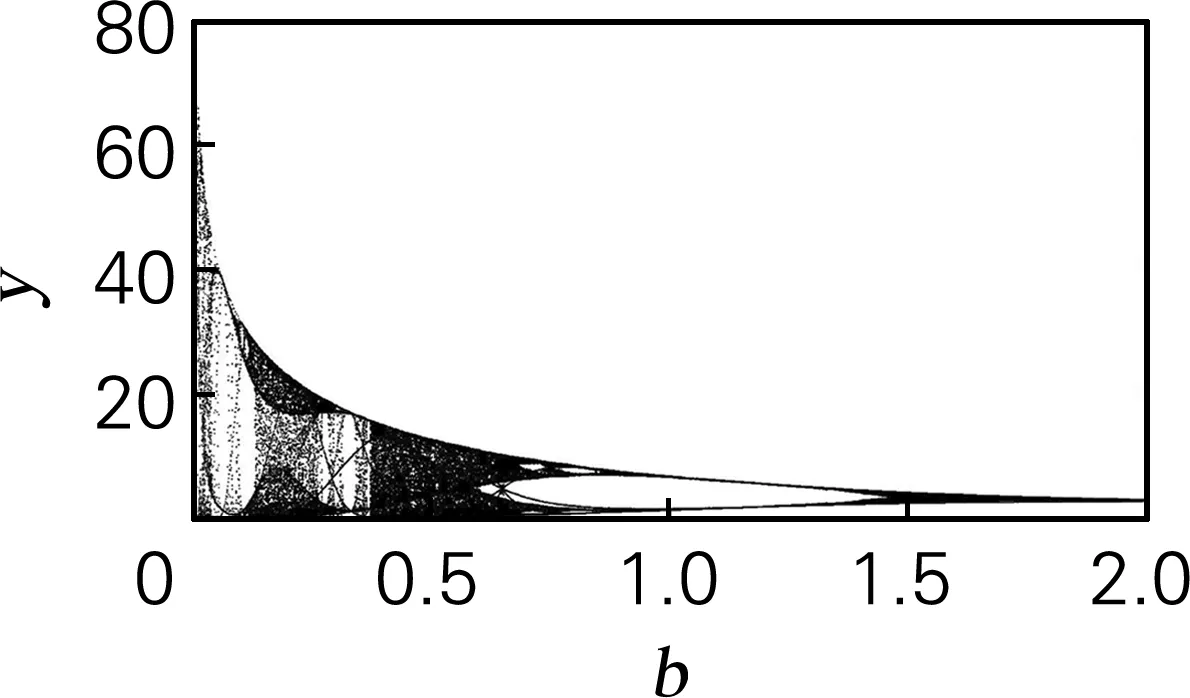
(c) 分岔图
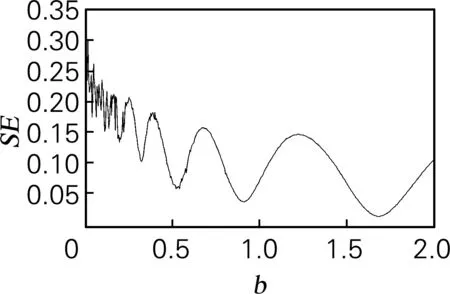
(d)SE复杂度
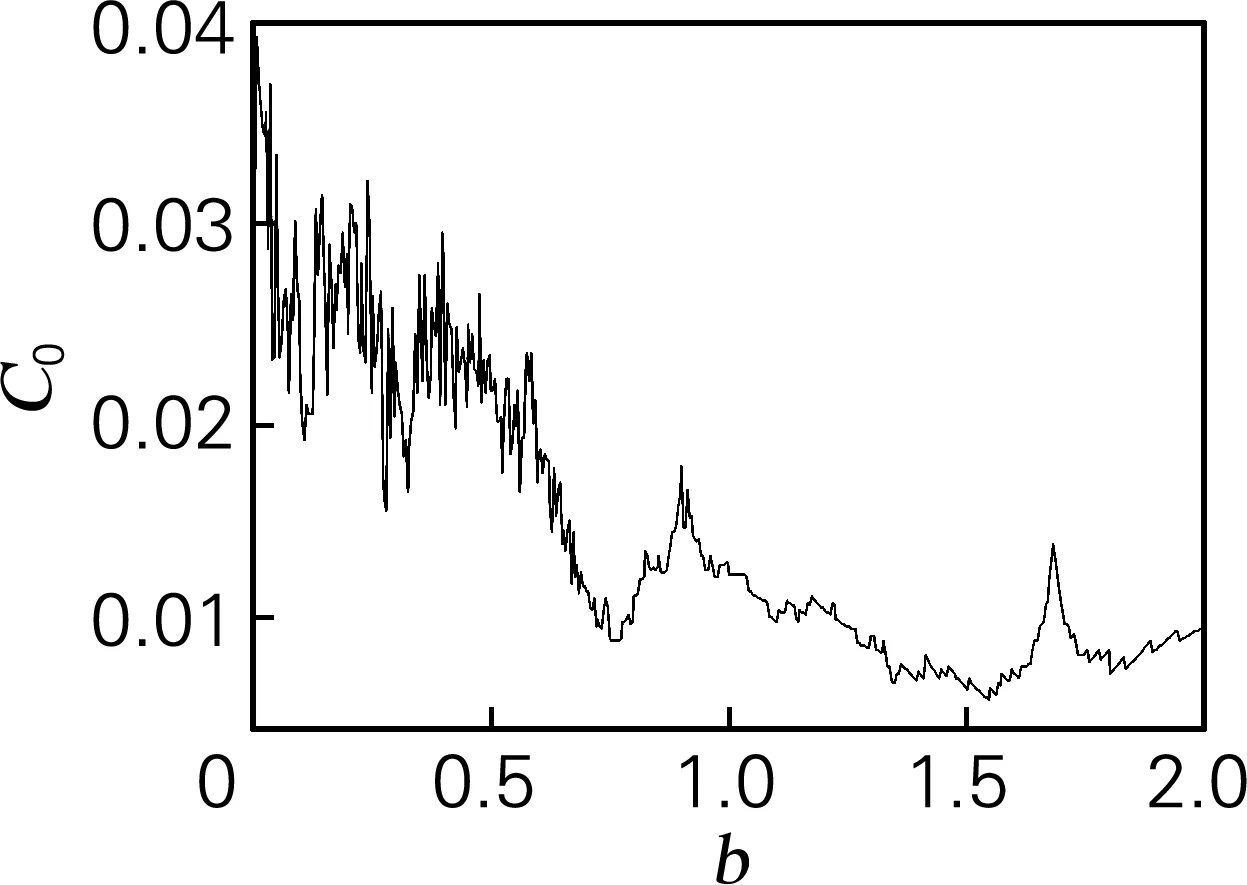
(e)C0复杂度
图2 Rossler系统仿真结果
Fig.2 Simulation results of Rossler system

(a) x-y平面相图
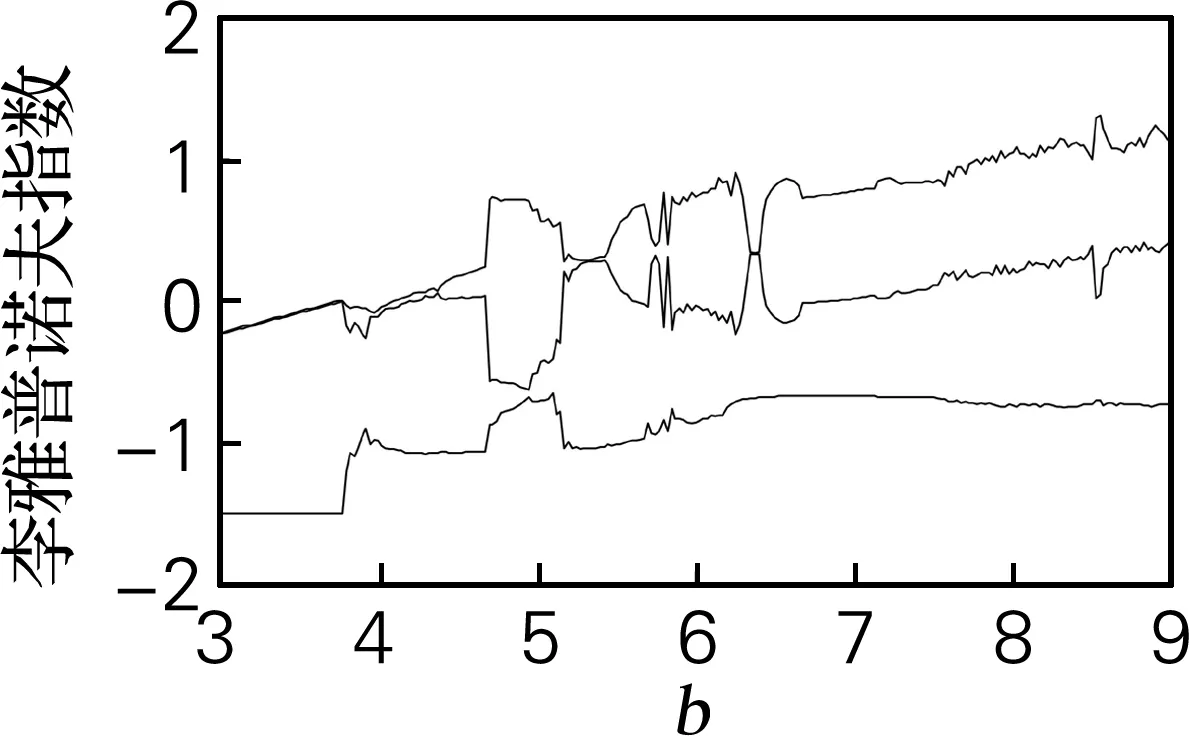
(b) 李雅普诺夫指数谱
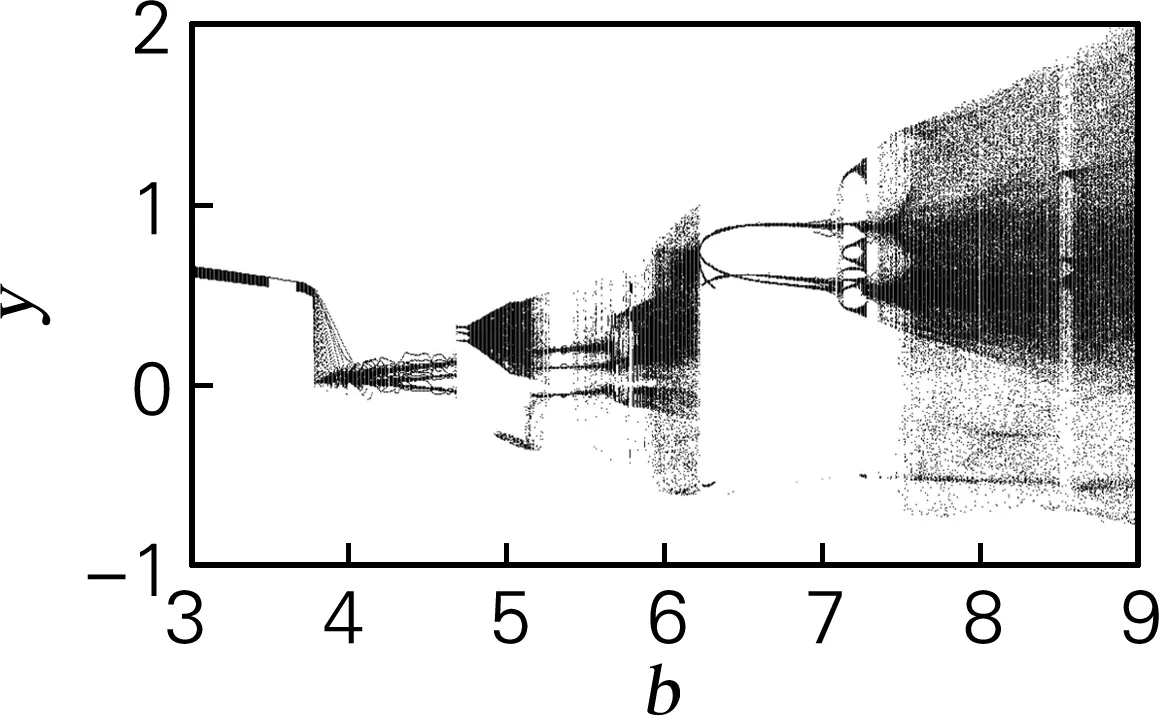
(c) 分岔图

(d)SE复杂度
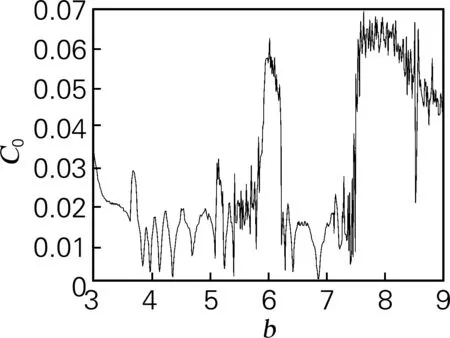
(e)C0复杂度
图3 文氏桥系统仿真结果
Fig.3 Simulation result of Wien-Bridge system
2.4 连续混沌系统的复杂度特性分析
对Bao、Rossler和文氏桥连续混沌系统分别从SE复杂度和C0复杂度的最大值和平均值进行比较分析。而对于文氏桥超混沌系统来说,选择其在混沌态和超混沌态时的最大复杂度和平均复杂度进行对比研究,结果如表1所示。Bao混沌系统最大,其次是文氏桥超混沌系统和Rossler混沌系统。由此可见,在不同的混沌系统中混沌态和超混沌态时的复杂度大小关系并不能确定。对比Bao混沌系统和文氏桥超混沌系统在混沌态和超混沌态时的SE复杂度和C0复杂度的最大值和平均值可以看出,当同一系统处于超混沌态时序列的复杂度比混沌态时的大,但是对于不同混沌系统,并不能直接根据系统是处于超混沌态还是混沌态来比较复杂度的大小。由这两种算法的仿真验证结果可见,SE和C0复杂度算法的特性可以与原系统的各项特性基本保持一致,这主要是因为SE算法和C0算法都是基于傅里叶变换来表征序列的复杂性。
表1 连续混沌系统的复杂度特性对比
Tab.1 Comparison of complexity characteristics of continuous chaotic systems

系统SEmaxSEC0maxC0Bao混沌系统0.71620.43510.39220.1937Rossler混沌系统0.30130.10870.03920.0146文氏桥超混沌系统超混沌态0.53920.43360.06930.0482混沌态0.23640.10390.03690.0121
3 结 论
使用SE和C0两种新的混沌系统信号复杂度算法,选用Bao、Rossler和文氏桥混沌系统进行仿真,结果表明:
(1)SE和C0复杂度与李雅普诺夫指数、分数维和分岔图一样都可以描述混沌系统的动力学特征。
(2)在同一混沌系统中,超混沌态的复杂度一般大于混沌态时的复杂度,系统复杂度的最大值一般在超混沌态区间内得到。
(3)对于不同的混沌系统,系统的复杂度只与系统本身相关,而与该系统是超混沌态还是混沌态并无直接联系。一个超混沌系统的复杂度平均值或最大值并不一定大于另一个混沌系统的复杂度平均值或最大值。混沌系统的复杂度特性是其本身固有的属性,决定于参数的变化及对初值的选取。所以在实际选取混沌系统应用时,系统的混沌态和超混沌态都可以作为实验研究对象,两者并无优劣之分。
(4)SE复杂度和C0复杂度的变化趋势在连续混沌系统中的验证结果具有一致性,主要由于两者都是以傅里叶变换为基础来反映序列结构的复杂性。但是两者的具体数值相差较大,这是由算法本身决定的。
(5)通过3个系统的复杂度特性对比分析可以看出,系统复杂度值的振幅在一定范围内变化,即连续混沌系统的复杂度具有有界性,这也是混沌系统所固有的特性之一。基于SE和C0复杂度特性的研究,为混沌系统应用于密码学、保密通信、信息安全等领域提供了相关理论依据和实验指导。
[1] 牟俊,王智森,康丽.统一混沌系统的状态观测器同步控制及其在保密通信中的应用[J].大连工业大学学报,2008,27(2):162-166.
[2] CHEN W T, ZHUANG J, YU W X, et al. Measuring complexity using Fuzzyen, Apen and Sampen[J]. Medical Engineering and Physics, 2009, 31(1): 61-68.
[3] 孙克辉,贺少波,尹林子,等.模糊熵算法在混沌序列复杂度分析中的应用[J].物理学报,2012,61(13):71-77.
[4] 陈小军,李赞,白宝明,等.一种基于模糊熵的混沌伪随机序列复杂度分析方法[J].电子与信息学报,2011,33(5):1198-1203.
[5] 孙克辉,贺少波,盛利元.基于强度统计算法的混沌序列复杂度分析[J].物理学报,2011,60(2):90-96.
[6] LARRONDO H A, GONZALEZ C M, MARTIN M T, et al. Intensive statistical complexity measure of pseudorandom number generators[J]. Physica A: Statistical Mechanics and its Applications, 2005, 356(1): 133-138.
[7] KOLMOGOROV A N. Three approaches to the quantitative definition of information[J]. Problems of Information Transmission, 1965, 2(1/2/3/4): 157-168.
[8] LEMPEL A, ZIV J. On the complexity of finite sequence[J]. IEEE Transactions on Information Theory, 1976, 22(1): 75-79.
[9] PINCUS S M. Approximate entropy as a measure of system complexity[J]. Proceedings of the National Academy of Sciences of the United States of America, 1991, 88(6): 2297-301.
[10] BANDT C, POMPE B. Permutation entropy: a natural complexity measure for time series[J]. Physical Review Letters, 2002, 88(17): 1741-1743.
[11] 包伯成.混沌电路导论[M].北京:科学出版社,2013.
[12] BAO B C, LIU Z, XU J P. New chaotic system and its hyperchaos generation[J]. Journal of Systems Engineering and Electronics, 2009, 20(6): 1179-1187.
[13] BAO B C, LI C B, XU J P, et al. New robust chaotic system with exponential quadratic term[J]. Chinese Physics B, 2008, 17(11): 4022-4026.
[14] 陈士华,谢进,陆君安,等.Rossler混沌系统的追踪控制与同步[J].物理学报,2002,51(4):749-752.
[15] GOPAKUMAR K, PREMLET B, GOPCHANDRAN K G. Inducing chaos in Wien-Bridge oscillator by nonlinear composite devices[J]. International Journal of Electronic Engineering Research, 2010, 4(22): 489-496.
[16] WOLF A, SWIFT J B, SWINNEY H L, et al. Determining Lyapunov exponents from a time series[J]. Physica D: Nonlinear Phenomena, 1985, 16(3): 285-317.
[17] PHILLIP P A, CHIU F L, NICK S J. Rapidly detecting disorder in rhythmic biological signals: a spectral entropy measure to identify cardiac arrhythmias[J]. Physical Review Statistical Nonlinear and Soft Matter Physics, 2009, 79(1): 100-115.
[18] CHEN F, XU J H, GU F J. Dynamic process of information transmission complexity in human brains[J]. Biological Cybernetics, 2000, 83(4): 355-366.
[19] 蔡志杰,孙洁.改进的C0复杂度及其应用[J].复旦学报(自然科学版),2008,47(6):791-796.
[20] 孙克辉,贺少波,朱从旭,等.基于C0算法的混沌系统复杂的特性分析[J].电子学报,2013,41(9):1765-1771.

