一种基于格的属性多重加密方案
汤海婷,汪学明
(贵州大学 计算机科学与技术学院,贵阳 550025)
0 概述
传统的属性基加密方案最初是在欧洲密码年会上创造性提出的[1]。之后,相继有学者提出了各种ABE方案。文献[2]对属性加密体制进行细粒度的划分,由此引入了KP-ABE和CP-ABE这2种属性加密体制。文献[3]给出了一个隐藏策略的ABE方案,但该方案不能抗合谋性。文献[4]构造出能抵抗合谋攻击,访问结构复杂的高安全的CP-ABE方案。文献[5]提出了可追责的CP-ABE方案,分别在用户追责和属性授权机构追责下进行考虑,该方案的缺陷是仅支持与门操作。当前,大部分属性密码体制都是用双线性对来构建的。随着量子密码时代的到来,构建能抵抗量子攻击的密码[6]是迫切需要的。格密码[7]在后量子密码中具有很高的地位,利用格构造密码方案不仅能抵抗量子攻击,同时也能减少计算过程的复杂程度。
文献[8]开创性提出格密码学,它是基于特定格代数结构构造的。直到2008年,才有基于格的身份加密方案提出。文献[9]利用格构造了标准模型下安全的模糊身份加密方案。同年,文献[10]提出应用门限访问结构来构建格上的CP-ABE方案。文献[11]提出了可证明安全的基于格的属性加密方案,在线性秘密分享技术下构建基于格的属性加密方案,并用学习错误(Learning with Errors,LWE)问题[12]证明了方案的正确性。文献[13]用格构造多授权机构的ABE方案。在基于格的属性加密研究中,提高加解密运行效率,引入合适的访问结构一直是个热点课题。对格上密文策略的属性加密研究不多,而实现基于格的密文策略属性加密方案,使它能够支持表达能力更强的访问结构是当前研究的热点。本文利用文献[10]提出的格上的CP-ABE方案和文献[14]提出的基于属性的动态多重加密方案,构造基于格的属性多重加密方案,并严格推导方案的正确性和在LWE问题下的高安全性。
1 属性加密和格理论
1.1 CP-ABE方案形式化描述
方案的形式化描述包括初始化、密钥生成、加密和解密。相关内容和安全模型及具体的方案描述见文献[14]。
1.2 格的基本定义


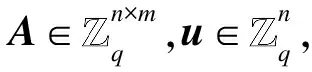

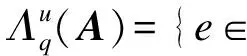
1.3 高斯分布
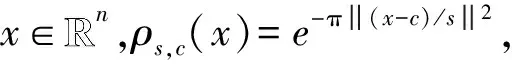

1.4 LWE问题
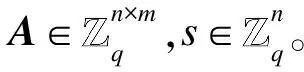
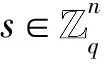
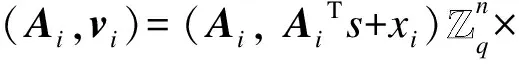
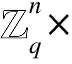
(Zq,n,χ)-LWE问题用一个算法来描述,其判定LWE问题的优势为|Pr[AOs=1]-Pr[AO$=1]|,若算法判定取样是属于OS,则输出0;否则输出1。算法对预言机多次询问后,其判定LWE问题的优势不可忽略,则称算法可以判定LWE问题。
格上的离散高斯抽样算法和相关引理见文献[15]。
2 基于格的属性多重加密方案
2.1 方案描述
引入一个松弛属性集合,它没有具体的意义,用来完成主密钥的构建。加入松弛属性集合可以支持更灵活的加密消息数量,也就是说用户在加密时更为灵活。采用文献[16]的多重秘密共享方案来生成用户的密钥,因为有松弛属性存在,使得本文方案具有动态性。
方案构造的第一步,生成发布多个系统主密钥来加密多个消息或者说可以加密一个很大的消息。这个很大的消息能够分组成多个长度较小的消息。由此,可以提高加解密效率。主密钥在生成过程中,利用多重秘密共享方案的思想,先转变成点值对,再融入到高次多项式里。在方案生成密钥的过程中,高次多项式会将主密钥msk分发到每个用户的解密密钥中。在文献[16]的方案中,每个用户仅维护一个秘密份额。这些秘密在重构过程中,只有拥有授权子集的参与者才能恢复每一个秘密,方案的加密过程可以同时加密多个消息。根据文献[10]提出的格上的CP-ABE方案,做出如下的构造。
2.2 方案具体构造
首先假设系统有y个属性,记松弛属性集合为Ω,它的个数为|Ω|=k。k表示同时加密的消息的数量。系统属性集合记为U={1,2,…,y},由文献[16],假设访问策略为Lpolicy,W为用户属性集合,且W⊂U,门限值为t。用户属性集合至少有t个属性才满足Lpolicy。
2.2.1 初始化
Setup(1λ):
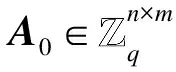
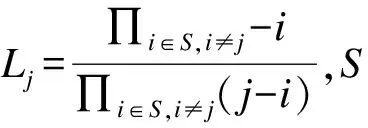
2.2.2 密钥生成
KGen(msk,w):
1)输入用户属性集合W。
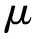
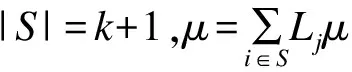
2.2.3 加密过程
Enc(pk,Lpolicy,Mv):
1)输入用户属性集W和公共参数pk,W满足Lpolicy,消息Mv∈{0,1},v∈[k]。
3)返回密文C=(Cv,C′,{Ciw}iw∈W,{CiΩ}iΩ∈Ω)。
2.2.4 解密过程
Dec(C,sk):
1)输入密文C、私钥ski、消息Mv,访问控制结构Lpolicy。
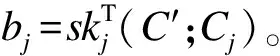
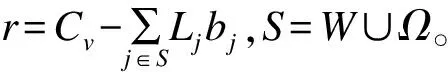
3 正确性证明
当|D∩W|≥t时,密文属性集满足用户属性集W,即属性集满足访问控制策略Lpolicy,由2.2.4节知:
同理得到(C′;CjΩ)的计算结果。

在解密算法中,计算:
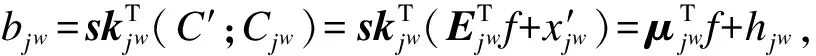
其中,h=∑j∈SLjhjs,则:
r=Cv-b=Cv-(μTf+h)=



4 安全性
4.1 安全性证明
假设存在一个多项式时间的算法能以ε>0的优势攻破上文的方案,则说明存在一个概率多项式时间的算法可以判定(Zq,n,χ)-LWE问题。
若敌手A能以不可忽略的概率解决(Zq,n,χ)-LWE问题,则方案就不安全。根据文献[10]的算法,相关过程如下:
Init:
1)敌手A给挑战者β发送了一个待挑战的访问结构Lpolicy。
2)令W*为待挑战的属性集合,它是敌手A将要攻击的目标。
3)A0和u是由LWE预言机随机产生,B由TrapGen算法产生。
Setup:
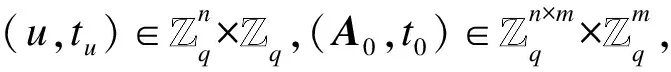
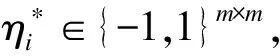
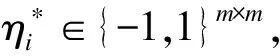

Phase1:
1)β收到私钥,产生询问,询问集合为θ,属性集满足|W*∩θ| Phase2:预言机重复Phase1中的行为。 Guess:敌手A给出对于预言机随机选取b的猜测值b′。若b′=b,那么预言机返回1,否则预言机输出0。 本文构造的方案结合文献[10,14]和一些相关算法,如果要保证方案的正确性和安全性,需要对参数进行如下设置: 2)方案开始阶段用到了TrapGen算法,这里要求m≥5nlogaq。 4)在安全性证明中,有: logaq+w(logan)。 5)在解密阶段,需要: 本文将格理论代替双线性对,构造了一个密文策略的属性多重加密方法。该方案可以同时加密多条消息,提高属性加解密效率,抵抗量子攻击并满足正确性要求。最后在LWE困难问题下证明了该方案的安全性。下一步将引入更为灵活的访问结构,并把方案拓展到大规模属性全集上。 [1] SAHAI A,WATERS B.Fuzzy Identity-based Encryption[C]//Proceedings of International Conference on Theory & Appli-cations of Cryptographic Techniques.Berlin,Germany:Springer,2005:457-473. [2] GOYAL V,PANDEY O,SAHAI A,et al.Attribute-based Encryption for Fine-grained Access Control of Encrypted Data[C]//Proceedings of the 13th ACM Conference on Computer & Communications Security.New York,USA:ACM Press,2006:89-98. [3] KAPADIA A,TSANG P P,SMITH S W.Attribute-based Publishing with Hidden Credentials and Hidden Policies[C]//Proceedings of Network and Distributed System Security Symposium.Washington D.C.,USA:IEEE Press,2007:179-192. [4] BETHENCOURT J,SAHAI A,WATERS B.Ciphertext-policy Attribute-based Encryption[C]//Proceedings of IEEE Symposium on Security and Privacy.Washington D.C.,USA:IEEE Press,2007:321-334. [5] LI Jin,REN Kui,ZHU Bo,et al.Privacy-aware Attribute-based Encryption with User Accountability[C]// Proceedings of International Conference on Information Security.New York,USA:ACM Press,2009:347-362. [6] BERNSTEIN D J,BUCHMANN J,DAHMEN E.Post Quantum Cryptography[M].Berlin,Germany:Springer,2011. [7] MICCIANCIO D,REGEV O.Lattice-based Cryptography[M].Berlin,Germany:Springer,2009. [8] AJTAI M.Generating Hard Instances of Lattice Problems[C]//Proceedings of the 28th ACM Symposium on Theory of Computing.New York,USA:ACM Press,1996:99-108. [9] AGRAWAL S,BOYEN X,VAIKUNTANATHAN V,et al.Functional Encryption for Threshold Functions (or Fuzzy IBE) from Lattices[M].Berlin,Germany:Springer,2012. [10] ZHANG Jiang,ZHANG Zhenfeng,GE Aijun.Ciphertext Policy Attribute-based Encryption from Lattices[C]//Proceedings of ACM Symposium on Information,Computer and Communications Security.New York,USA:ACM Press,2012:16-17. [11] BOYEN X.Attribute-based Functional Encryption on Lattices[M].Berlin,Germany:Springer,2013. [12] REGEV O.On Lattices,Learning with Errors,Random Linear Codes,and Cryptography[J].Journal of the ACM,2009,56(6):34. [13] ZHANG Yanhua,HU Yupu,JIANG Mingming.An Attribute-based Signature Scheme from Lattice Assumption[J].Wuhan University Journal of Natural Sciences,2015,20(3):207-213. [14] 郭振洲.基于属性的加密方案的研究[D].大连:大连理工大学,2012. [15] 冯 芳.格上基于属性的加密算法研究[D].西安:西安理工大学,2015. [16] 庞辽军,姜正涛,王育民.基于一般访问结构的多重秘密共享方案[J].计算机研究与发展,2006,43(1):33-38.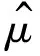
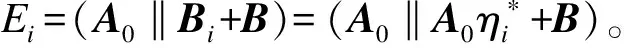
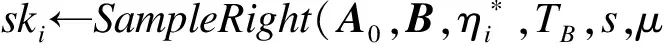
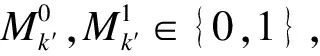
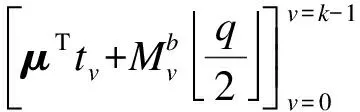
4.2 参数估计

5 结束语

