一种稀疏度自适应的稀疏傅里叶变换算法
刘 仲,李立春,李慧启
(信息工程大学 信息系统工程学院,郑州 450001)
0 概述
在信号处理领域,离散傅里叶变换(Discrete Fourier Transform,DFT)是最基本的算法之一。而快速傅里叶变换(Fast Fourier Transform,FFT)是最快的DFT算法之一,其算法复杂度只有O(nlogan)。目前,计算DFT的算法复杂度为Θ(n),均与信号长度成正比。在图像处理[1]、宽带频谱感知[2-4]、机器学习理论[5]、多尺度分析[6]、卫星通信[7]等众多科学领域中,许多实际信号都有一定程度的稀疏性或可压缩性。这种结构特殊、广泛存在的信号成为了信号处理领域热门的研究方向。针对离散傅里叶变换,几种频域稀疏的亚线性算法[8-11]相继被提出,但这些算法由于结构的限制只适用于非常稀疏的信号。
近几年,稀疏快速傅里叶变换(sparse Fast Fourier Transform,sFFT)算法成为研究稀疏信号的一大热点,并相继提出了一些实用的sFFT算法。该类算法利用信号频域的稀疏性对频率进行“分桶”,使DFT运算的点数成倍减少,然后通过其他方法实现对原信号完整频谱的重构,从而使算法的复杂度与信号长度成亚线性关系,进而提高信号处理速度。近年来稀疏傅里叶变换的算法硕果累累,研究人员提出了许多算法。这些算法降低了算法复杂度[12-13],拓宽了维度适用范围[14],并实现了算法的并行加速[15],并且推广到了其他变换域[16]。但稀疏傅里叶变换都需要信号以傅氏域的稀疏度为先验信息,通常稀疏度K是未知的,在一定程度上限制了上述算法的应用。为此,针对未知稀疏度的信号,本文提出一种稀疏度自适应的稀疏傅里叶变换算法(Sparsity Adaptive Algorithm for Sparse Fast Fourier Transform,SAsFFT)。
1 稀疏傅里叶变换算法
稀疏傅里叶变换算法通过时域降维对频域稀疏的信号进行处理,将信号的频域信息压缩到低维空间中,在快速傅里叶变换后,通过定位和估值2个环节重构得到频域信号。稀疏傅里叶变换算法的流程如图1所示。
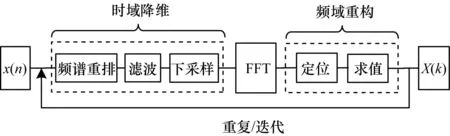
图1 稀疏傅里叶变换算法流程
1.1 信号的稀疏表示

x=Fs
(1)
其中,s是信号x在正交基F上的投影系数向量。若s中只有K个系数不为0,其他N-K个系数全为0,那么信号x在频域上是K-稀疏的,K表示信号x的稀疏度。若s中K个系数值较大,其他N-K个系数很小,且几乎为0,则称信号x在频域上是近似K-稀疏的。若一个信号在频域上能够被稀疏表示,则该信号可进行稀疏傅里叶变换,也可以降维到低维空间中。
1.2 时域降维
如果信号在频域能够被稀疏表示,当设置若干个桶且桶数比频率数更多时,那么按照一定规则将各个有效频率分到这些桶中,每个桶中只存在唯一的频率。从频域角度考虑,将每个桶视为一个序列单元,那么长序列可被映射为短序列。对短序列进行快速傅里叶变换,则算法复杂度将大幅度降低。sFFT的时域降维过程可以表示为:
y=ΨB×Nx
(2)
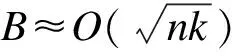
将每一桶作为一个序列单元进行处理,其方法是取桶中的一个有效频点代表该桶的值,该步骤称为下采样。下采样对x中的元素按索引进行等间隔的累加,其处理过程如式(3)所示。
(3)

为保证取到每一个有效频点,利用频域卷积定理,将时域信号与窗函数2个矢量相乘,则在频域上各桶内唯一存在的有效频点展宽成多个频点,这样在下采样时就能够取到有效频点。本文所使用的窗函数取自文献[11]的平滑窗函数。
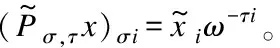
1.3 频域重构
在正交频分复用(OFDM)技术的频偏估计方法中,2个采样点之间的相位差与频点坐标呈线性关系。渐近法从相位差角度出发,运用该原理中不同频率所对应相位不同的特点,通过对相位区间进行能量检测判断有效频率的存在与否。该类方法可对相位二分查找,或划分成多区段查找[17]逐步迭代得到频率。二分渐近法保证了算法的鲁棒性,但复杂度相对较高;相比之下多区段渐进法速度较快,复杂度较低,但鲁棒性较差。
统计法主要从重复统计角度出发,利用哈希映射、孙子定理[11]等方法先确定下采样所对应频域中存在频点的桶,反推出原始信号中可能包含的频率,通过改变重排参数对哈希逆映射的多次统计,或对不同参数下得到的线性同余方程求解,得到原始信号中的有效频率。由于统计法的重排随机进行,因此会产生一定的频率冲突。在每次循环中存在的虚警也会产生极少量的重构信息误差[17]。但统计法均衡了算法复杂度和鲁棒性,该方法性能较为稳定,具有较好的研究前景。
2 稀疏度自适应的稀疏傅里叶变换算法
为解决未知稀疏度的问题,基于sFFT-1算法的优势,本文提出了SAsFFT算法。本节从算法总体流程、稀疏度估计的影响因素和稀疏度的确定3个部分介绍SAsFFT算法。
2.1 算法总体流程
SAsFFT利用了信号的频域稀疏性,在信号稀疏度未知的前提下,通过迭代逐步估计得到信号的稀疏度,从而使算法适用于未知稀疏度的信号。SAsFFT与现有的sFFT算法相比,其改进在于增加了对稀疏度的估计和检测过程。该算法可以分为3个步骤,其总体流程如图2所示。


步骤3有效分量筛选。对稀疏傅里叶变换的结果进行能量检测,剔除无效的虚警分量,得到最终的k个傅氏域信息。
图2SAsFFT算法流程
2.2 稀疏度估计的影响因素
利用第2.1节中信号的稀疏特性,以及稀疏傅里叶变换中时域降维的性质对频域稀疏的离散信号进行稀疏度的估计得到预测稀疏度。稀疏度估计的流程如下:
子步骤1初始化预测稀疏度;
子步骤2时域降维;
子步骤3快速傅里叶变换;
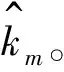
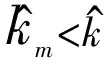
对预测稀疏度准确性的影响因素主要有2个:频谱碰撞和窗函数卷积。本节主要从以下的2个方面进行分析。
2.2.1 频谱碰撞的影响
稀疏度决定了一个信号变换到下采样域后的矢量维度,进而影响频谱碰撞概率。首先可推导在未知稀疏度的条件下,设定稀疏度与碰撞概率的关系。文献[11]给出了定理1,该定理限定了非零系数落入同一桶中的概率。
定理1若j≠0,n是2的幂次方,σ∈[1 ,n]是一个随机奇数,则Pr[σj∈[-C,C]mod n]≤4C/n。
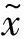
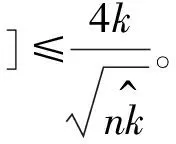
证明:令bi为下采样域的第i个元素。考虑任意i,j∈S,由定理1有:
Prσ,τ[bi=bj]≤ Prσ,τ[|(σi+τ)mod n-(σj+τ)mod n|<
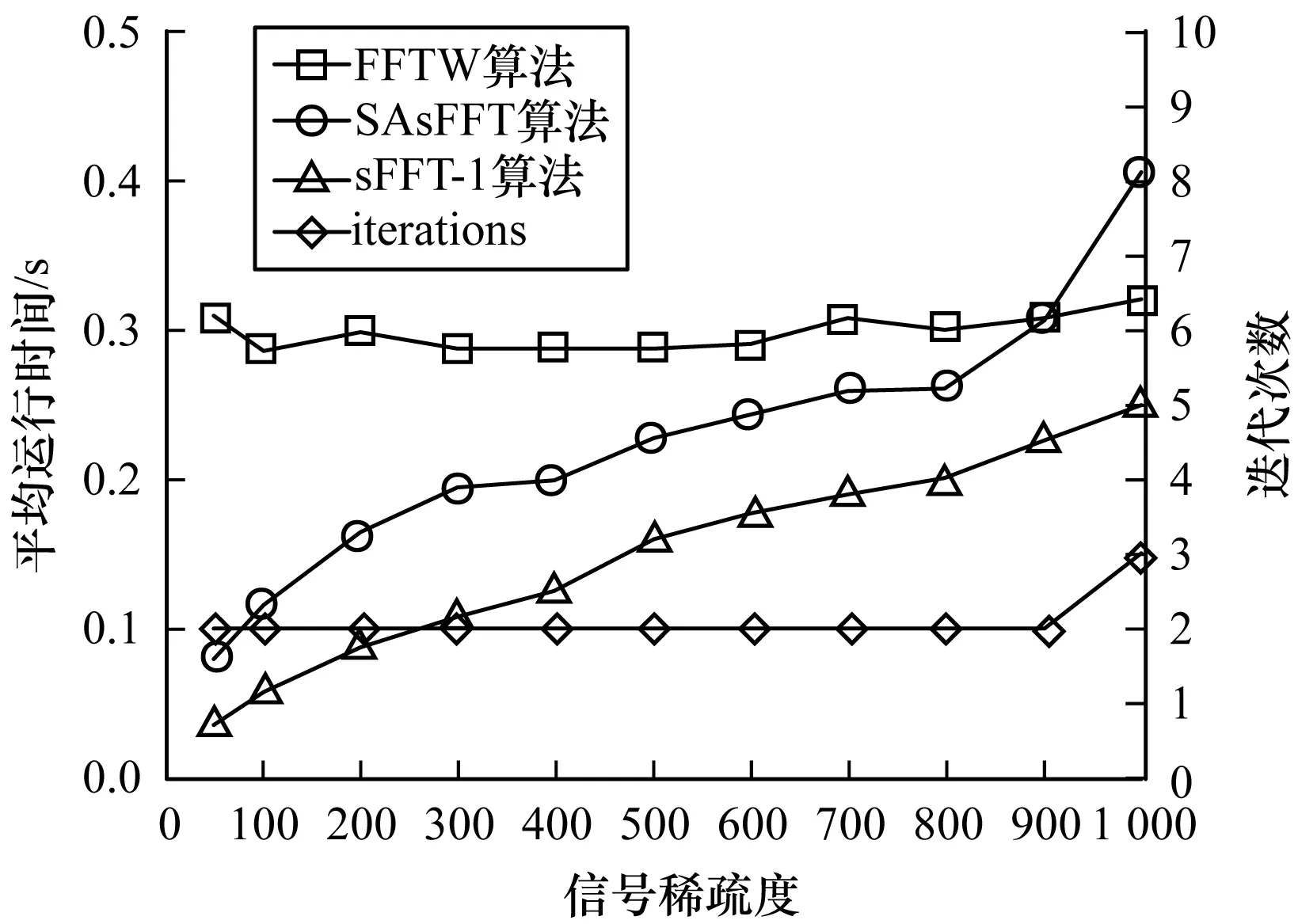
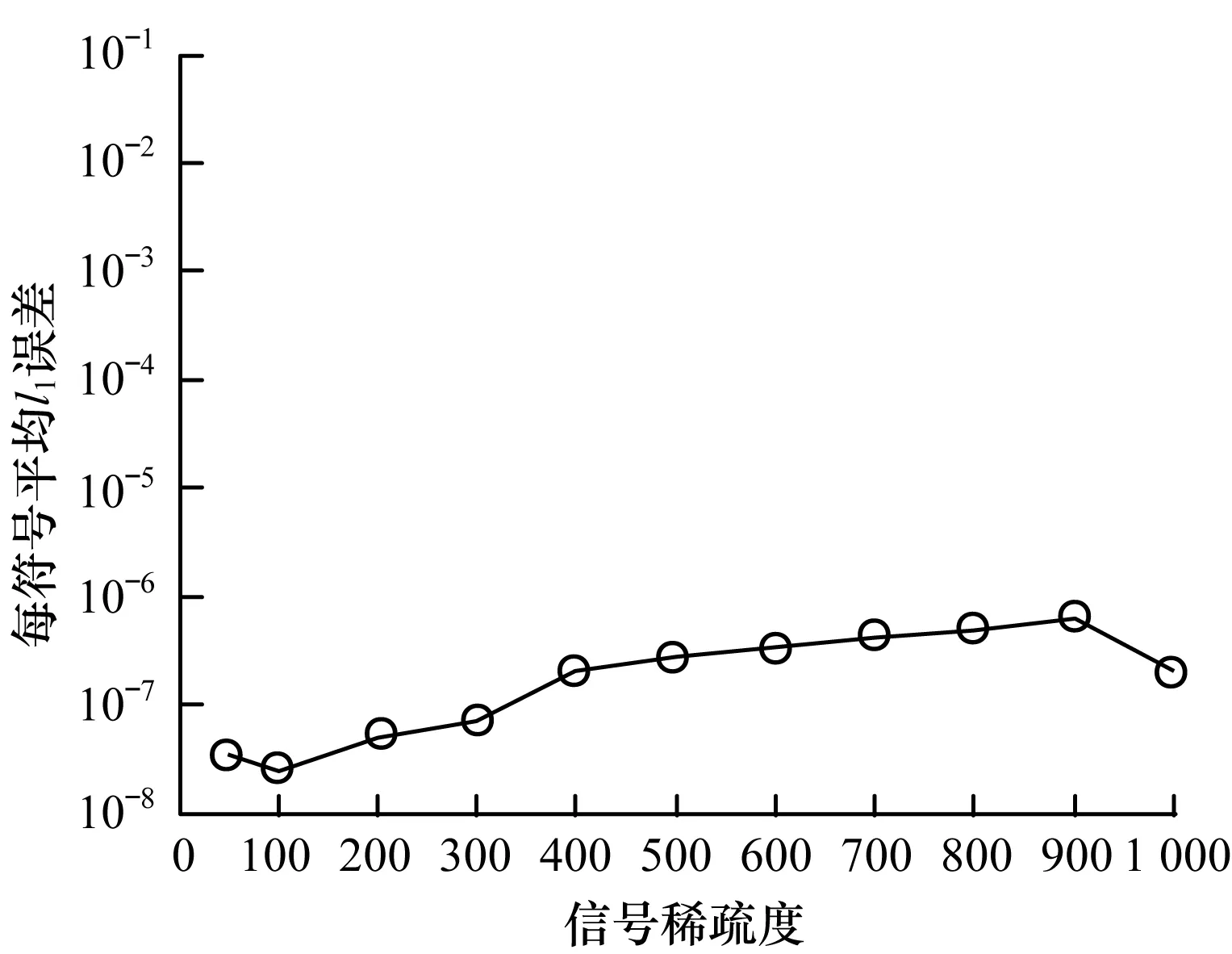
n/B]=Prσ,τ[|σ(i-j)|mod n 那么,从原时域的角度考虑,对于信号矢量x有: 得证。 2.2.2 窗函数卷积的影响 本节阐明窗函数的卷积会对信号中有效频率产生虚警,使得估计的频率数增加,导致预测稀疏度大于真实稀疏度。 根据文献[17]中的定理3.3,以及对本文算法中信号和窗函数的假设,对降维过程结果可得如下的推论。 (4) 为了验证SAsFFT的可行性和鲁棒性,本节对SAsFFT、FFTW和sFFT-1 3种算法进行了仿真实验。仿真实验分别是在不同信号长度、不同稀疏度下的算法对比,以及SAsFFT算法的鲁棒性仿真。本文算法中所采用测试信号的产生方式参考了文献[9]。时域降维过程使用的窗函数为2.2节中所定义的窗函数。 信号参数设置如下:信号x的矢量长度为n,在信号的傅氏域上从[1,n]中随机选择k个分量,各分量的幅度为1,相位随机,其他分量设为0。在仿真结果中,每个点代表不同参数的信号,每个点是经过100次独立的重复实验的平均结果。在实验中,与SAsFFT算法进行对比的是FFTW(the Faster Fourier Transform in the West)和sFFT-1[11]。 实验平台采用Ubuntu Linux 16.04版本,处理器为Intel(R) Core(TM) i5-4210M CPU @ 2.60 GHz,内存为8 GB。 对于本文实验,固定信号稀疏度参数k=50,选择了8个不同的信号长度分别为n=217,218,…,224。在不同的信号长度下,对同一信号分别运行SAsFFT、 FFTW和sFFT-1,得到3种算法的平均运行时间对比如图3所示。 图3 不同信号长度的算法平均运行时间对比 从图3中可以发现,在横坐标为对数分度时,SAsFFT、FFTW和sFFT-1的运行时间均呈线性关系,SAsFFT和sFFT-1的斜率基本相同,且比FFTW的斜率小。SAsFFT与sFFT-1相比,在不同信号长度下SAsFFT的平均运算时间均相对较长,但平均运算时间差比较稳定。同时,由图3可知,若信号稀疏度k=50,当信号长度n>219时,则SAsFFT运算速度比FFTW快。信号长度越长,SAsFFT的平均运算时间越短,其运算速度优势体现就越明显。 对于本文实验,固定信号长度参数n=222,选择了11个不同的信号稀疏度k=50,100,200,…,1 000。在不同的信号稀疏度下,对同一信号分别运行SAsFFT、FFTW和sFFT-1,得到3种算法的平均运行时间对比如图4所示。 图4 不同信号稀疏度的算法平均运行时间对比 从图4可以观察到,FFTW在不同信号稀疏度下运算时间基本保持不变,而SAsFFT和sFFT-1的平均运算时间均呈线性关系。在不同信号稀疏度下SAsFFT的平均运算时间比sFFT-1长,但两者的平均运算时间差也比较稳定。当信号长度固定不变时,信号稀疏度为900,SAsFFT与FFTW的平均运算时间基本相等。因此,综合来看,对于小于900的信号稀疏度,SAsFFT的运算时间更快。 除此之外,图4给出了不同稀疏度下SAsFFT算法的迭代次数。当稀疏度k≤900时,迭代次数维持在2次,可见SAsFFT的稀疏度估计过程比较稳定,即SAsFFT算法的运算时间比较稳定,不会出现较大波动。 (5) 在不同的信号稀疏度下,对同一信号分别运行SAsFFT,得到该算法的每符号平均l1误差对比,如图5所示。 图5 不同信号稀疏度的鲁棒性对比 由图5可以得到,对于固定长度的信号,算法不同信号稀疏度的每符号平均l1误差都小于10-6,算法保持了较高的稳定性,完全可以满足绝大部分信号的实际应用需求。 本文提出一种基于稀疏度自适应的稀疏傅里叶变换算法。该算法根据频谱碰撞和窗函数卷积对频率检测的影响估计,得到一个稍大于真实稀疏度的预测稀疏度,通过已有的稀疏傅里叶变换后,在算法的输出中剔除冗余数据,从而得到较好的结果。根据数学理论分析和算法运行的实验结果表明,该算法实现了未知稀疏度条件下的稀疏傅里叶变换,扩展了稀疏傅里叶变换算法的应用范围;算法运算量小,复杂度低,在运算时间上快于传统FFT算法,且完成傅里叶变换后的效果理想,验证了算法的可靠性。 [1] CHANDRAKASAN A,GUTNIK V,XANTHOPOULOS T.Data Driven Signal Processing:An Approach for Energy Efficient Computing[C]//Proceedings of International Symposium on Low Power Electronics and Design.Washington D.C.,USA:IEEE Press,1996:347-352. [2] DONOHO D L.Compressed Sensing[J].IEEE Transac-tions on Information Theory,2006,52(4):1289-1306. [3] CANDES E J,WAKIN M B.An Introduction to Com-pressive Sampling[J].IEEE Signal Processing Magazine,2008,25(2):21-30. [4] 卢 迅,李立春,李 鸥,等.非重构压缩样值跳频信号时频联合估计算法[J].信息工程大学学报,2016,17(4):425-430. [5] LINIAL N,MANSOUR Y,NISAN N.Constant Depth Circuits,Fourier Transform,and Learnability[J].Journal of the ACM,1989,40(3):607-620. [6] DAUBECHIES I,RUNBORG O,ZOU A J.A Sparse Spectral Method for Homogenization Multiscale Problems[J].Siam Journal on Multiscale Modeling & Simulation,2007,6(3):711-740. [7] 范星宇.低轨卫星星载通信信号处理关键技术研究[D].北京:北京理工大学,2014. [8] GILBERT A C,GUHA S,INDYK P,et al.Near-optimal Sparse Fourier Representations via Sampling[C]//Proceed-ings of ACM Symposium on Theory of Computing.New York,USA:ACM Press,2002:152-161. [9] GILBERT A C,MUTHUKRISHNAN S,STRAUSS M.Improved Time Bounds for Near-optimal Sparse Fourier Representations[C]//Proceedings of SPIE’05.Washington D.C.,USA:IEEE Press,2005:398-412. [10] IWEN M A,GILBERT A,STRAUSS M.Empirical Evaluation of a Sub-linear Time Sparse DFT Algorithm[J].Communica-tions in Mathematical Sciences,2007,5(4):981-998. [11] IWEN M A.Combinatorial Sublinear-time Fourier Algori-thms[J].Foundations of Computational Mathematics,2010,10(3):303-338. [12] HASSANIEH H,INDYK P,KATABI D,et al.Simple and Practical Algorithm for Sparse Fourier Transform[C]// Proceedings of ACM-SIAM Symposium on Discrete Algorithms,Society for Industrial and Applied Mathematics.New York,USA:ACM Press,2012:1183-1194. [13] 孟祥玉,李 静,彭 华.一种基于迭代更新的稀疏傅里叶变换改进算法[J].信息工程大学学报,2016,17(6):669-674. [14] INDYK P,KAPRALOV M.Sample-optimal Fourier Sampling in Any Constant Dimension[C]//Proceedings of the 55th IEEE Annual Symposium on Foundations of Computer Science.Philadelphia,USA:IEEE Press, 2014:514-523. [15] WANG C,MAURICIO A P,CHANDRASEKARAN S,et al.Parallel Sparse FFT[C]//Proceedings of Workshop on Irregular Applications:Architectures and Algorithms.New York,USA:ACM Press,2013:10-23. [16] 周广福,文成林,高敬礼.基于小波变换与稀疏傅里叶变换相结合的光场重构方法[J].电子学报,2017,45(4):782-790. [17] HAITHAM H,INDYK P,KATABI D,et al.Nearly Optimal Sparse Fourier Transform[C]//Proceedings of the 44th ACM Symposium on Theory of Computing.New York,USA:ACM Press,2012:563-578.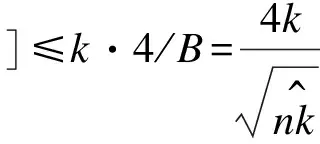
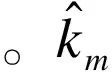

2.3 信号稀疏度的确定
2.4 算法复杂度分析
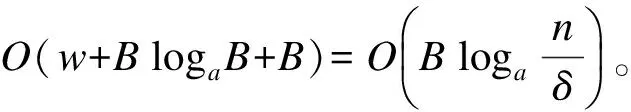

3 仿真结果与分析
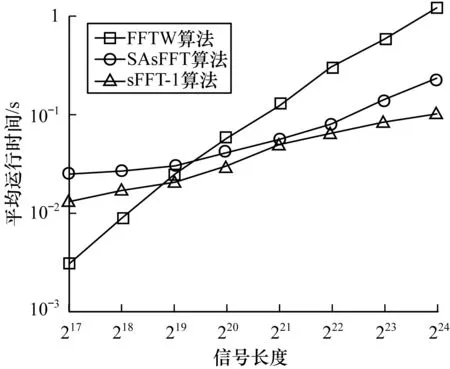
3.1 信号长度对不同算法的影响比较
3.2 信号稀疏度对不同算法的影响比较
3.3 信号稀疏度对算法鲁棒性的影响

4 结束语

