扭曲椭圆管强化传热的场协同分析

马芳芳,,,

(1.山东建筑大学 热能工程学院，山东 济南 250101；2.可再生能源建筑利用技术省部共建教育部重点实验室，山东 济南 250101；3.山东省可再生能源建筑应用技术重点实验室，山东 济南 250101)

0 引言

扭曲管是由换热器中的普通换热管通过压扁后扭曲而成，由于扭曲管的多点自支撑结构，与传统圆管换热器相比，扭曲管换热器具有传热系数高、压降小、少结垢、无振动、易清洗等一系列特点[1]。流体在管内周期性的螺旋流动可以使流体冲刷壁面，减薄边界层，同时引起流体的二次流动，促进流体的径向混合。并且国内外不少学者已经对螺旋椭圆扭曲管单向扭曲的换热流动情况进行了研究并取得了不少成果。例如我国的梁龙虎[2]对螺旋椭圆管与光管的换热和阻力情况作了实验对比研究；张杏祥[3]等对螺旋椭圆管的传热与流阻特性经行了模拟分析；刘敏珊[4]等模拟了螺旋椭圆管与螺旋扁管在雷诺数小于1 000时的换热特性；高学农[5]等研究了高扭曲比的螺旋椭圆管的传热与流阻性能。张杏祥、桑芝富[6]等人证明了螺旋扭曲扁管换热器壳程整体性能指标a/Δp较高；螺旋扭曲扁管换热器管程与壳程都有较好的强化传热性能。根据刘伟等[7]指出，可以通过调节流场，减小速度矢量U和温度梯度矢量T之间的夹角来实现强化传热；减小速度矢量U和压降梯度矢量-P之间的夹角来实现流动减阻。本文采用CFD的流固共轭传热技术对扭曲管进行了数值模拟，模拟了以水为流体的管道内速度场、压力场及温度场，并且依据场协同原理对其强化传热的影响因素及其变化规律进行了深入分析，以及获得扭曲椭圆管强化传热的影响机理。

1 几何模型及控制方程

1.1 几何模型

在数值计算中，扭曲椭圆管扭曲2π即为一个扭程S。选取长L=300 mm，截面为椭圆且长轴a=20 mm、短轴b=10 mm，且扭曲周期依次递增的扭曲扁管进行数值模拟，如图1所示。

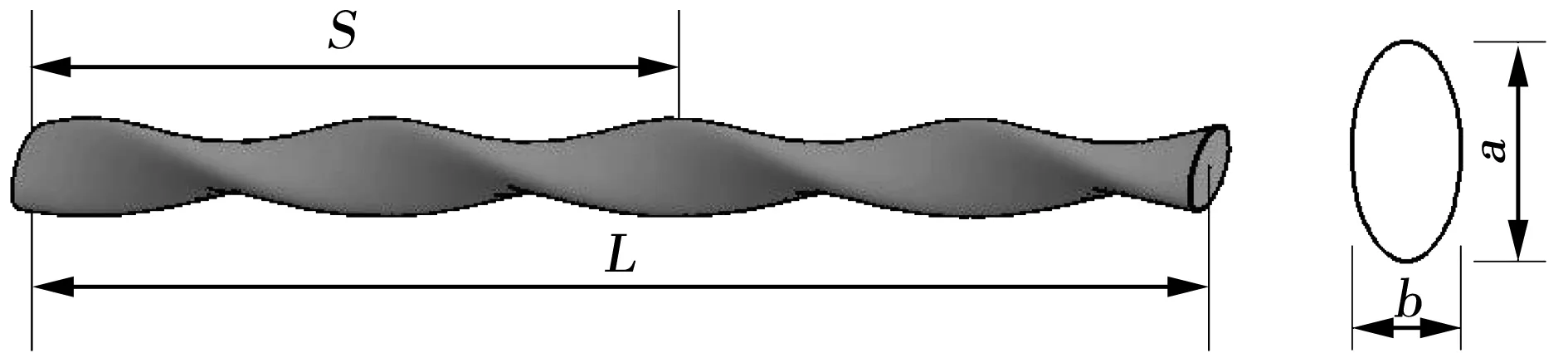
图1 扭曲扁管几何模型

在数值模拟中，扭曲椭圆管的管壁材料设置为铝，因该模拟主要着重于管内流体的传热及流阻，故暂不考虑壁厚影响，设壁厚为零。

为研究扭曲椭圆管扭曲角度对其传热及流阻性能影响，模拟计算选取不同扭距多周期的扭曲椭圆管，根据扭曲椭圆管总相等，扭转周期为整数原则，扭曲椭圆管参数如表1所示。

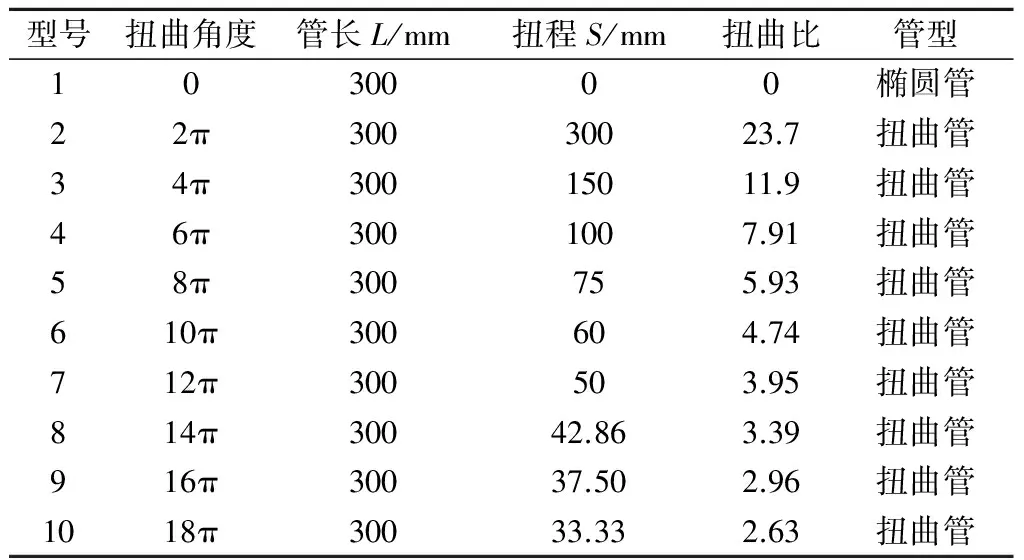
表1 不同扭曲椭圆管

扭曲比即为扭距S比上当量直径d，所有型号的扭曲椭圆管送水速度和水的初始温度均分别为0.01 m/s和293.15 K，管道壁面给定壁温353.15 K。

1.2 控制方程

以扭曲椭圆管的整个流动区域中的流体为研究对象，建立数学模型。管道内流体流动的控制方程[8]为

连续性方程

(1)

动量方程

(2)

能量方程

(3)

式中u——流体的x方向速度分量/m·s-1；

v——流体的y方向速度分量/m·s-1；

w——流体的z方向速度分量/m·s-1；

p——流体的压力/Pa；

T——流体的温度/K；

η——流体的动力粘性系数/Pa·s；

a——流体的热扩散系数/m2·s-1；

ρ——流体的密度/kg·m-3；

ρ0——流体的参考工作密度/kg·m-3；

x——x方向的矢量/m；

y——y方向的矢量/m；

z——z方向的矢量/m。

2 求解方法

采用CFD建立物理模型并划分网格，计算过程中采用有限容积法离散方程，同时求解流体的连续性方程，动量方程和能量方程。选取层流模型，采用二阶迎风差分格式进行离散，控制方程的求解利用SIMPLE算法。进口边界条件给定水的进口平均流速、进口温度；出口边界条件设定相对压力为零。当能量方程中收敛残差小于10-6时，整个计算过程被认为收敛。所有的计算过程都进行了网格无关性检验。并且做了如下假设：(1)水的物性参数为常数；(2)流体在壁面上无滑移；(3)流体的流动是定常的；(4)不考虑在重力方向上浮升力的影响。

3 计算结果及比较

因几何模型之间区别仅为扭曲周期，各模型之间流体流动的区别仅为旋转缓急，流动总体趋势一致，故取其中扭曲角度为2π的几何模型为例进行解释。

3.1 速度场与温度场的分析

图2为管内扭曲处截面速度场及温度场，扭曲椭圆管内的流动有着很强的旋转特性，从图中可看出由于管道的扭曲导致流体流动方向的扭曲变形，靠近壁面的边界层处可以看出，流体有冲击边界层的趋势，通过模拟可以看出：扭曲管结构使得管内流体产生旋转流动，迫使流体改变了流动方向，在扭转同时使流体冲击了管道壁面，削弱了热边界层，并且扭曲程度越大，这个趋势越明显，从而流体速度与温度梯度的协同程度就越好，这有利于强化换热。

图2 管内扭曲处截面速度流线图及温度图

3.2 速度场与温度场的协同分析

层流的能量协同方程[9]

(4)

式中Nu，Re，Pr——努塞尔数、雷诺数和普朗特数；

无因次速度与无因次温度梯度的点积可表达为

U·T=|U||T|cosβ

(5)

若矢量U与矢量T之间的夹角越小，则点积U·T越大，努塞尔数Nu越大，流体与壁面间的对流换热也就越强。从而可推出协同角表达式为

(6)

基于场协同原理及公式可得出速度与温度梯度的协同程度即协同角。取扭曲角度为18π的管道与扭曲角度为2π的管道的协同角云图及等值线图进行对比解释，如图3所示。

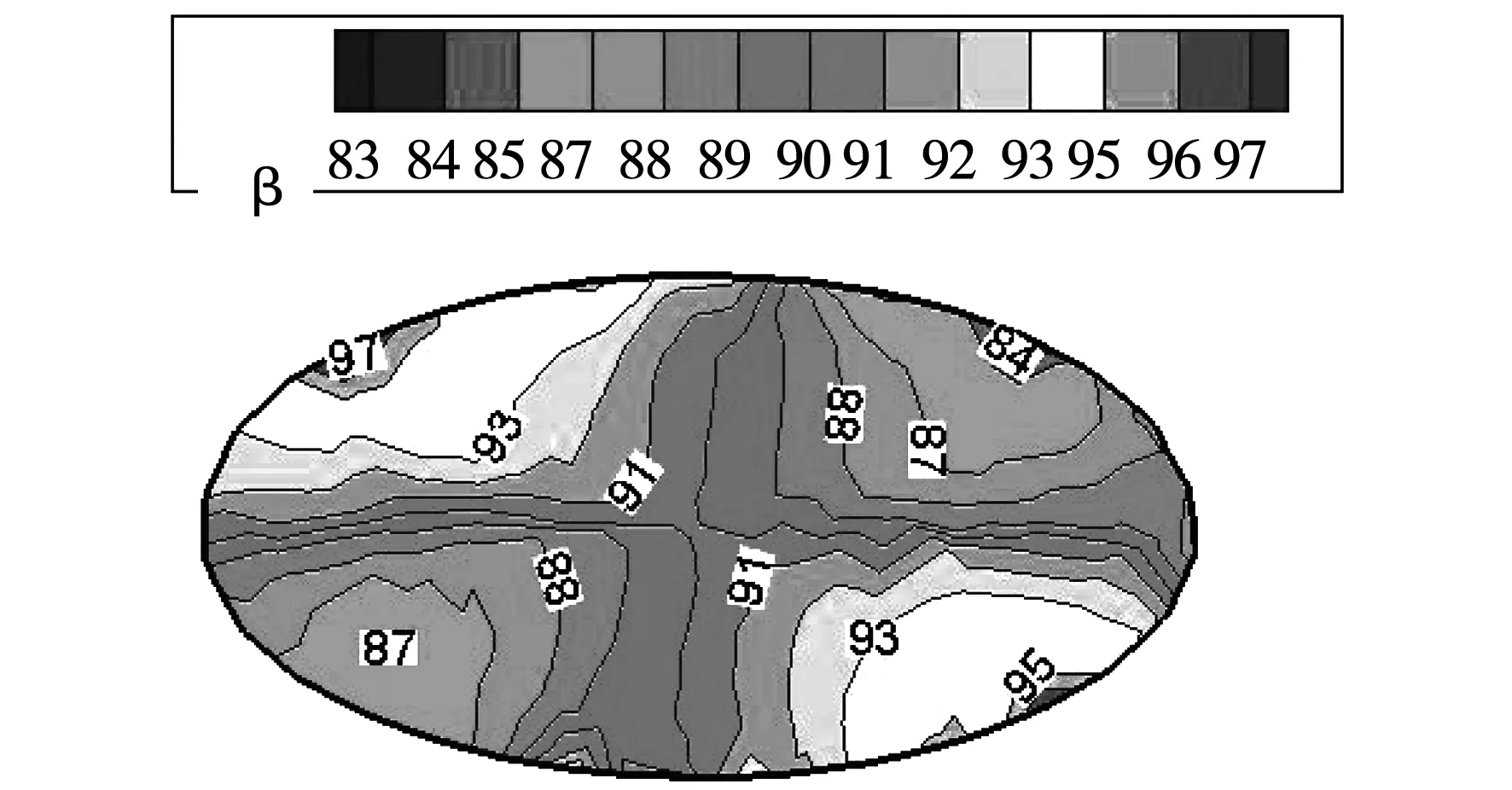
图3 扭曲2π管道扭曲90°截面处的协同角等值线

图4 扭曲18π管道扭曲90°处截面的协同角等值线

如图3所示：图中右上角以及左下角的协同角小至约84°，由于管道扭曲的作用使得管内流体产生旋转流动，致使流体冲击管壁，热边界层减薄，致使此处速度与温度梯度的协同程度较好，达到强化传热的效果。左上角以及右下角的协同角逐渐增大至约97°，由于管道的扭曲而造成的流体旋转流动致使流体在此处并没有冲击壁面，即此处速度与温度梯度的协同程度很差，不仅不强化传热，甚至弱化传热。由图4可知，随着管道扭曲程度的加大造成流体的旋转流动更加急促，管道扭曲90°截面处，右上角及左下角协同角趋近70°，说明此处由于流体的旋转流动急促程度的加大，热边界层越薄，速度与温度梯度的协同程度越好。但是左上角及右下角趋近110°，说明随着流体旋转流动的急促程度导致流体在此处越远离壁面，速度与温度梯度的协同程度越差。

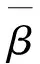
表2 管道扭曲90°处速度与温度梯度的平均协同角

由表2可以看出，管道截面平均协同角随扭曲程度的加大逐渐减小。根据公式(6)可知β值越小，则点积U·T越大，相应努塞尔数Nu越大，流体与壁面间的对流换热也就越强。由此可知扭曲椭圆管的扭曲比越小，强化换热效果也就越好。

3.3 速度场与压力场的分析

图5 扭曲椭圆管x=0处截面速度流线图及压力图

图5为扭曲管的速度场和压力场，带有箭头的流线为速度流线，竖向直线为截面图中压力等值线。由于管道的扭曲导致管道内速度会呈周期性重新分布，管道入口处边界层处压力等值线与速度矢量线近似平行，即压降梯度与速度矢量近似垂直，故此处速度与压力梯度协同程度较差，而管道中心主流区压力等值线与速度矢量线都近似垂直，即压降梯度与速度矢量线基本平行，故管道中心主流区速度与压力梯度的协同程度较好。

3.4 速度场和压力场的协同分析

速度U与压力梯度之间的协同关系表达为[9]

U·(-P)=|U||-P|cosθ

(7)

从而可推出协同角表达式为

(8)

若点积U·(-P)一定，θ角越小，流体的功耗|U||-p|越小。由此可见, 减小协同角θ意味着降低流体消耗的泵功, 提高设备的节能效果。

基于场协同原理及协同角公式可得速度与压力梯度的协同角。协同角云图如图6所示。

图6 扭曲椭圆管x=0处截面协同角云图

由表3可以看出，管道截面平均协同角随扭曲程度的加大逐渐增大。根据公式(8)可知θ值越大，流体的功耗|U||-p|越大。由此可知扭曲椭圆管的扭曲比越小，管道内的流动阻力损失也就越大。

3.5 扭曲扁管综合性能分析

将扭曲椭圆管传热性能、阻力性能和综合传热性能分别整理为传热增强因子Nu/Nu0，阻力增大因子f/f0，及综合传热性能增强因子η。

扭曲扁管的Nu、f，η分别定义为[10]

(9)

(10)

(11)

式中q——流体热流密度/J·m-2·s-1；

d——通道的当量直径/m；

Twall——壁面温度/K；

Tref——参考温度/K,取管内流体混合平均温度；

λ——流体导热率/W·m-1·K-1；

ΔP——管段进 出口压降/Pa；

L——管段长度/m；

ρ——流体密度/kg·m-3；

U——流道截面的平均速度/m·s-1。

根据以上模拟结果以及计算结果，通过流体速度场和压力场协同程度以及速度场和温度场协同程度的定量分析，可以得出以下各管道之间的比较图。

如图7与图8所示：根据比较可明显得出，随着管道扭曲程度的增大，Nu逐渐增大，认为强化换热效果依次变强。且各型号管道速度与温度梯度在扭曲角度为90°处的平均协同角随着管道扭曲程度的增大也逐渐减小，根据速度场与温度场的协同分析，认为整个流动区域内，流动速度与温度梯度的协同程度越好即协同角越小，换热效果就越好。故可知随着管道扭曲程度的增大，管道的强化换热效果越好。

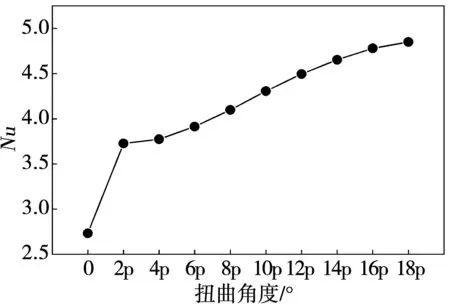
图7 各型号管道努谢尔数比较图

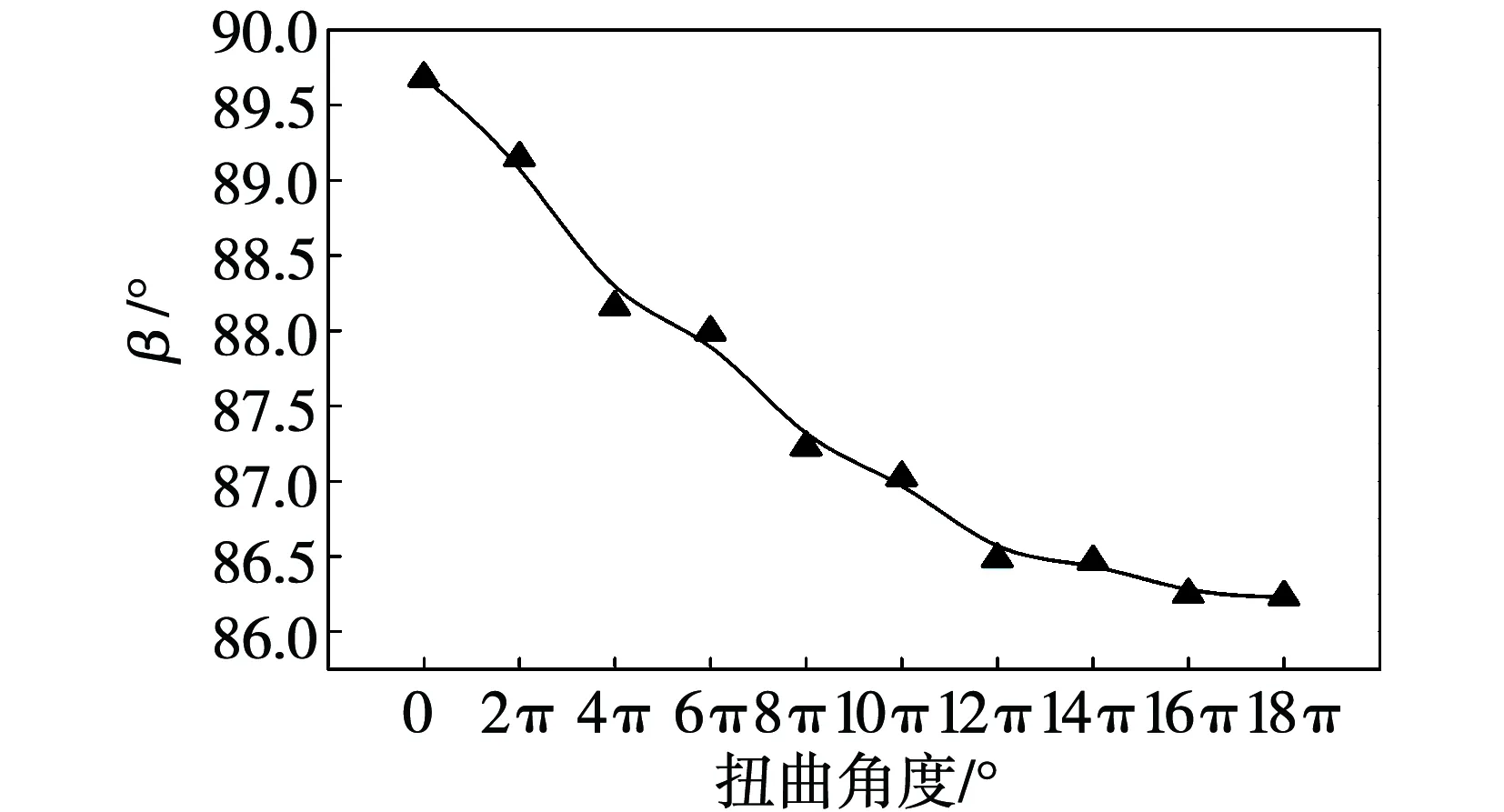
图8 各型号在扭曲角度为90°处的平均协同角

如图9与图10所示：根据比较可以明显看出，随着管道扭曲程度的增大，f逐渐增大，认为流动阻力系数越大。且各型号管道速度与压力梯度平均协同角随着管道扭曲程度的增大逐渐增大，根据速度场与压力场的协同分析，认为整个流动区域内，流动速度与压力梯度的协同程度越差即协同角越大，阻力系数就越大。故可知随着管道扭曲程度的增大，管道的流动阻力损失也就越大。

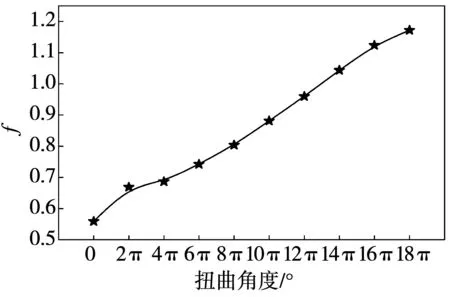
图9 各型号管道达西阻力系数比较图

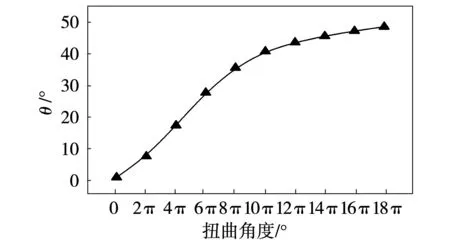
图10 各型号管道速度与压力梯度平均协同角图

如图11所示：根据比较可知，随着管道扭曲程度的增大，综合强化传热因子逐渐增大且均大于1，说明相比于椭圆管，扭曲椭圆管可以强化管内传热，且随着管道扭曲程度的增大，强化换热效果越好。可知扭曲管具有较好的强化换热性质，由此可对工程进行优化节能。

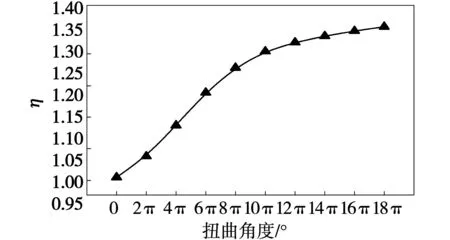
图11 各型管道综合传热性能增强因子比较图

4 结论

通过利用CFD软件对管道内的流体流动进行数值模拟，发现流体的速度场和温度场协同程度直接影响管道的换热能力，以及压力场和速度场协同程度直接影响管道的流动阻力损失。基于场协同原理进一步获得管道内流动流体的速度与温度梯度的平角协同角，以及速度与压力梯度的平均协同角，并以此平均协同角和经过计算所得管道的综合传热性能增强因子为评价指标得出扭曲管的换热性能的好坏。计算结果表明:

(1)由于扭曲椭圆管的特殊结构形式，使管内流体做纵向旋转流动，形成垂直于主体流速的二次流，因此可以削弱传热边界层，强化管内流体传热。虽然也使管内流体的流动阻力损失有所增大，但是扭曲管管内的强化传热综合性能仍然优于椭圆直管。

(2)通过数值模拟结果显示，扭曲管的扭曲比S/d越小，扭曲管的强化传热性能就越好，但是同时流阻也会增大。

(3)流体速度场与温度场协同程度越好，强化传热效果越好；流体速度场和压力场协同程度越差，则局部阻力损失越大。

(4)本文研究表明，利用CFD软件对管道内流体流动进行基于场协同原理的数值模拟，可有效实现管道内流体流动方案的比较，为工程上的开发和设计强化换热的管道提供理论依据。

[1]鞠在堂.螺旋扁管换热器[J].化工装备技术,2003,24(5):19-22.

[2]梁龙虎.螺旋扁管换热器的性能及工业应用研究[J].炼油设计,2001,8(31):28-33.

[3]张杏祥,桑芝富.螺旋扭扁管强化传热与阻力性能的模拟分析[J].化工机械,2006,33(1):24-28.

[4]刘敏珊,宫本希,董其伍.螺旋扁管的换热性能研究[J].石油机械,2008,2(36):22-25.

[5]高学农,邹华春,王端阳,等.高扭曲比螺旋扁管的管内传热及流阻性能[J].华南理工大学学报(自然版),2008,11(36):17-21.

[6]张杏祥,桑芝富.螺旋扭扁管强化传热与阻力性能的模拟分析[J].化工机械,2006,33(1):24-29.

[7]刘伟,刘志春,过增元.对流换热层流流场的物理量协同与传热强化分析[J].科学通报,2009,54(12):1779-1785.

[8]陶文铨.数值传热学[M].西安:西安交通大学出版社，1998.

[9]刘伟，刘志春，马雷.多场协同原理在管内对流强化传热性能评价中的应用[J].科学通报,2012(10):867-874.

[10]Webb R L, Eckert E R G. Application of rough surfaces to heat exchanger design[J]. International Journal of Heat & Mass Transfer,1972,15(9):1647-1658.

[11]朱冬生,石仲璟,钱泰磊,等.扭曲椭圆管换热器的数值模拟及场协同分析[J].高校化学工程学报,2015(1):64-71.

[12]张洋乐.不同扭距扭曲管管内流场的数值模拟[J].石油化工设备技术,2016,37(3):13-16.

[13]Amin Ebrahimi, Ehsan Roohi. Numerical study of flow patterns and heat transfer in mini twisted oval tubes[J].International Journal of Modern Physics C,2015,26(12):295-307.

[14]Cheng J, Qian Z, Wang Q. Analysis of heat transfer and flow resistance of twisted oval tube in low Reynolds number flow[J]. International Journal of Heat & Mass Transfer, 2017:761-777.

[15]韩勇,王定标,张灿灿,等.椭圆内肋扭曲管换热性能数值研究[J].工程热物理学报,2015,36(12):2707-2710.

[16]GUAN Ping, AN Fangtao, LU Mei. Numerical Simulation on Heat Transfer Performance of Laminar Flow Outside Twisted Oval Tube[M].Light Industry Machinery,2016.